基于元胞自动机的城市地表径流流向优化算法
何梦男,陈 诚,李 港,胡智华,何湖滨,陈求稳,6
(1.南京水利科学研究院生态环境研究所,江苏 南京 210029; 2.四川大学水利水电学院,四川 成都 610044;3.河海大学水利水电学院,江苏 南京 210098; 4.重庆交通大学河海学院,重庆 400074;5.浙江省交通规划设计研究院有限公司,浙江 杭州 310030;6.水文水资源与水利工程科学国家重点实验室,江苏 南京 210029)
近年来,快速的城市化进程在改变地表下渗过程的同时增加了各种复杂陡、缓地形,使得城市地表水力梯度组成纷繁复杂。城市水文模型可为城市内涝预警和面源污染防控提供重要的决策工具,其发展需要适应城市地表复杂变化的特征,从而实现城市降雨径流过程的精确模拟[1-3]。其中,水流流向是城市水文模型中表征地表径流的重要参数,描述了水流在不同地表地貌单元之间从高到低的流动路线。流向算法是众多城市水文模型中计算水流流向的基本方法,影响着汇水面积、地形指数等参数的计算[4],在城市水文模型研究中起着重要作用。
目前流向算法主要分为单流向(single flow direction,SFD)算法和多流向(multiple flow direction,MFD)算法,均假设局部水力梯度可用局部坡度估计[4-5]。单流向算法是将水力梯度最大的相邻单元作为水流的下游单元,具有计算简单、效率高等优势[6]。单流向算法往往趋向于形成收敛的直线,而实际情况中水流有可能是漫散流态,因而单流向算法一般适合模拟水流在陡坡面上的流动,不适合模拟缓坡面上的漫散流动。而多流向算法的方法学原理主要基于“越陡下游方向获取的水量越多”和“动力系统倾向于往平衡状态发展”两种假设[7],将水量按照分配权重p分配至不同的下游单元中。水量分配权重是指水量分配到各个网格的权重,用于描述水流从当前时刻到下一时刻的运动过程。有关学者基于水量分配权重的不同取值,提出了FD8、FMFD、MFDfg等多流向算法[8-9]。虽然多流向算法可以弥补单流向算法模拟缓坡漫散流的缺陷,但目前多流向算法中水量分配权重多为固定值,忽略了地形特征对流场划分的影响,在坡度较陡的情况下模拟结果往往较差[10]。因此,如何兼顾单流向算法与多流向算法的优点,构建适用于城市地表复杂水力梯度的径流优化算法对于城市水文过程模拟具有重要意义。
元胞自动机(Cellular Automata,CA)是大量个体通过局部联系组成的时间、空间以及状态均离散的数学方法。在水文学和土壤侵蚀研究领域,通常被用于快速洪涝[11-13]和泥沙冲淤演变模拟[13],已被实践证明是一种适合复杂系统模拟的离散化数学工具,不仅能避免微分方程求解,还可有效减少数值计算的复杂度。
本文在考虑城市地表复杂水力梯度特征的前提下,提出一种基于元胞自动机的城市径流流向优化算法,通过计算元胞邻域各单元水位值标准差,得到直接反映局部水力梯度的指标,并设计流态判断规则以弥补其他多流向算法的不足。

图1 Moore型邻域Fig.1 Moore type neighborhood
1 材料与方法
1.1 元胞自动机模型
元胞自动机模型主要包括元胞空间、邻域、状态和规则四部分,其中元胞规则是元胞自动机的核心,主要是流态判断规则,定义了元胞从当前时刻状态向下一时刻演变的法则,决定了元胞自动机模型的演化方向。元胞邻域采用典型的Moore型邻域,如图1所示。元胞状态除了元胞索引坐标(x,y)、边长l以及时间步长t以外,还包括表征产汇流过程的地表特征、径流两部分状态,见表1。

表1 元胞状态参数
1.2 流向优化算法
基于元胞自动机的城市径流流向优化算法(the optimal urban flow direction algorithm based on Cellular Automata,UCA)流程如图2所示,主要分为3个步骤:

图2 UCA算法流程Fig.2 Flowchart of UCA algorithm
步骤1转移时间计算。比较中间元胞与邻域元胞的水位值,排除水位值高于中间元胞的邻域元胞,将剩下的邻域元胞作为可转移水量的下游元胞,再根据式(1)计算中间元胞水量全部转移到各个下游元胞所需时间:
(1)

步骤2流态判断。设置流态判断规则对漫散流态与汇聚流态进行定量区分,主要根据9个元胞高程(水深)值标准差(SD)与标准差阈值(SD0)的大小进行判断:
(2)
(3)

步骤3转移水量计算。先根据式(4)(5)确定各个下游元胞的水量分配比例di,再根据式(6)对比每个元胞转移时间与模型时间步长的大小,计算时间步长内转移至各个下游元胞中的水量Ri。
(4)
(5)
(6)
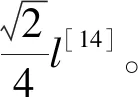
(7)

1.3 流向算法试验

图3 两种坡面示意图Fig.3 Illustrations of two slopes
为筛选漫散流态和汇聚流态时各自水量p的最优值,考虑如图3所示的陡、缓坡面流问题:x方向和y方向长度分别为500 m和100 m,坡度β分别为0.20和0.05。稳定、均匀的超渗降雨落于坡面,降雨强度I为100 mm/h,降雨历时为25 min,模拟时长为60 min,坡面水力糙率采用曼宁系数表示,取值为0.01。假定初始时刻坡面处于干燥状态,l=1.0 m,采用UCA算法求解坡脚出口处的流量过程线,并利用罗志等[15]提出的坡面流解析解(analytical solution)作为参考进行定量评价。
为定量评价UCA算法在不同地形条件下的性能,采用不同算法模拟计算了城市中常见的凸坡、凹坡、山脊和直坡上的单位汇流面积(specific catchment area,SCA)。单位汇流面积指单位长度等高线上的汇流面积,是定量描述地表水流分布的重要水文参数,通常可以对比SCA的模拟值与理论值对流向算法进行定量评价。采用l=1.0 m及4种人工数学曲面[5-6,9](椭球面、反椭球面、马鞍面和斜面)分别代表城市中常见的凸坡、凹坡、山脊和直坡。人工数学曲面的优点是可以通过数学推导获得汇流面积的理论值,其定义及对应的SCA理论值如图4所示。参与对比的算法有单流向D8算法、固定水量分配权重的FMFD算法、UCA算法和基于差异最小化的4+4N算法。

图4 人工数学曲面及其单位汇流面积理论值Fig.4 Artificial mathematical surface and its theoretical value of SCA
采用均方根误差(root mean square error,RMSE)、纳什效率系数(Nash-sutcliffe efficiency coefficient,NSE)和平均绝对误差(mean absolute error,MAE)对模拟结果进行评价。
2 结果与分析
2.1 水量分配权重筛选
在坡度较缓时,Quinn等[16-17]认为水量p=1.0可以模拟水流完全漫散的情况,Freeman[17]通过对比p=1.0、1.1和1.25情况下的模拟效果,认为p=1.1可作为缓坡漫散流态情况下最优水量分配权重。因此,设置水量p=1.1、2.0、5.0、8.0、10.0等5种工况下的坡面流模拟试验。不同水量分配权重下出口流量模拟统计结果见表2。由表2可以看到,不同水量分配权重出口流量陡坡条件下的纳什效率系数都很好,接近于1,而均方根误差有明显的区别。按照均方根误差越接近于0,纳什效率系数越接近于1的选择依据,可看出在城市地区陡坡汇聚流态和缓坡漫散流态的最优水量分配权重分别是2.0和1.1。

表2 不同水量分配权重下出口流量统计结果
2.2 汇流面积差异分析
图5~图8分别为凸坡、凹坡、山脊坡以及直坡面上不同流向算法求解的单位汇流面积与其理论值差异。对比4种算法在各坡面上汇流面积差异结果,可看到D8和4+4N算法单位汇流面积与理论值有差异的区域面积明显大于FMFD算法,说明D8和4+4N算法的单位汇流面积模拟结果与理论值差异相对较大,而FMFD算法的单位汇流面积模拟结果与理论值差异小于D8和4+4N算法。同时,对比UCA算法和FMFD算法的各坡面汇流面积差异结果,可以看到UCA算法和FMFD算法在4种地形条件下模拟结果最接近,且在凹坡面上UCA算法的结果与理论值有差异的区域与FMFD算法相当,而在凸坡面、山脊和直坡面上UCA算法的结果与理论值有差异的区域面积比FMFD算法更小,说明UCA算法在FMFD算法的基础上进一步实现了优化。

图5 凸坡面上不同流向算法求解的单位汇流面积与其理论值差异Fig.5 Difference between theoretical SCA and calculated SCA by different flow direction algorithms on convex surface

图6 凹坡面上不同流向算法求解的单位汇流面积与其理论值差异Fig.6 Difference between theoretical SCA and calculated SCA by different flow direction algorithms on concave surface

图7 山脊坡面上不同流向算法求解的单位汇流面积与其理论值差异Fig.7 Difference between theoretical SCA and calculated SCA by different flow direction algorithms on ridge

图8 直坡面上不同流向算法求解的单位汇流面积与其理论值差异Fig.8 Difference between theoretical SCA and calculated SCA by different flow direction algorithms on plane surface
2.3 算法性能定量评价
图9为不同流向算法求解的单位汇流面积与其理论值的误差频率分布。相比之下可以看到每个坡面上UCA算法的相对误差分布最集中于0附近,相对误差值在[-20,20]之间的元胞比例分别为99.84%、89.01%、99.89%和99.80%,在[-5,5]之间的元胞比例分别为89.61%、68.22%、84.72%和80.92%。FMFD算法次之,而D8算法和4+4N算法的误差频率相对分散。总体来看,UCA算法模拟结果与理论值的相对误差最小。

图9 不同算法求解的单位汇流面积与其理论值的误差频率分布Fig.9 Error frequency distribution of theoretical SCA and calculated SCA by different algorithms
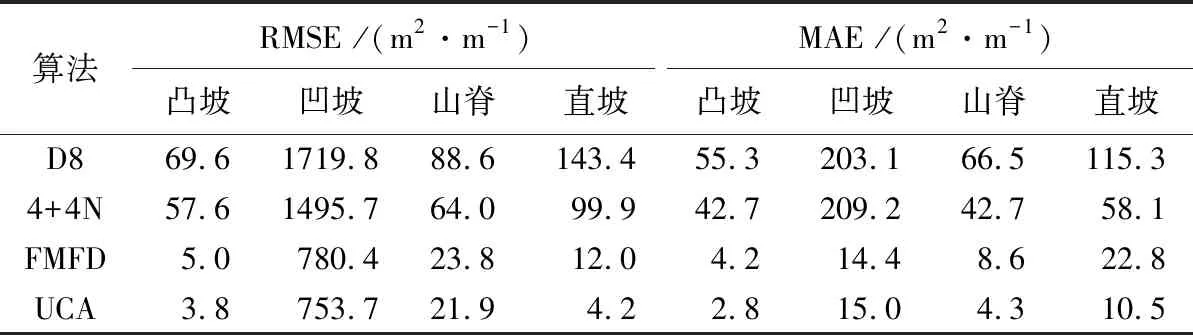
表3 不同算法定量评价结果
为进一步定量评价算法的性能,统计不同算法模拟单位汇流面积的均方根误差和平均绝对误差,结果见表3。从不同坡面的两种误差结果来看,4种算法在不同坡面上的误差从大到小均呈现凹坡大于直坡大于山脊大于凸坡的趋势。4种径流算法在凸坡面的模拟效果均最好,而在凹坡面(反椭球面)上的均方根误差最大,这是由于反椭球面底部的径流过程属于汇流填洼,流向算法对该复杂流向区域的概化本身就存在误差[5],再加上反椭球面底部等高线长度无穷小,误差又被无穷小的等高线进一步放大。
城市地形中常见的路面、屋面等多属于直坡面[14,18]。从表3每种算法的误差结果来看,D8算法在直坡面上的误差均较大,而在凸坡面和山脊面上的误差相对较小,说明D8算法适用于模拟凸坡、山脊这类陡坡汇聚的径流过程,而不适用于模拟直坡这类缓坡漫散的径流过程。4+4N算法相对于D8算法增加了在对角线方向分配水流的可能,因而在4种坡面上的误差相比于D8算法有所减小。FMFD算法较D8和4+4N算法的误差进一步显著减小,说明FMFD算法固定水量分配权重的方式可以有效弥补D8和4+4N算法不适用于模拟缓坡漫散流的缺陷。
UCA算法在FMFD算法的基础上考虑了局部地形特征变化,采用水量分配权重随地表特征进行变化的方式处理水流多流向分配问题。从表3还可以看到UCA算法在4种坡 面上的均方根误差相比于FMFD算法进一步减小,特别是对于直坡面上的漫流情况,UCA算法的均方根误差为4.2 m2/m,相比于FMFD算法12.0 m2/m减小了近3倍,说明UCA算法不仅适合模拟城市平坦地形上的缓坡漫散流,还适合模拟城市局部地形变化较大坡面上的收敛汇聚流。从平均绝对误差结果来看,UCA算法和FMFD算法在凹坡地形单位汇流面积模拟结果中,与其理论值的平均绝对误差很接近,分别为15.0 m2/m和14.4 m2/m;而在凸坡、山脊和直坡上,UCA算法的单位汇流面积模拟结果与理论值的平均绝对误差均最小,分别为2.8 m2/m、4.3 m2/m和10.5 m2/m。总体而言,UCA算法比FMFD算法更接近单位汇水面积理论值。
3 讨 论
城市道路最大纵坡度受设计车速等因素限制,一般不低于8.0%;草地设计坡度通常较缓,一般在1.5%~12.0%;城市屋面常设为平坡面,坡度一般小于5.0%[18]。这些常见的下垫面表面径流过程趋于漫散,而在坡度较大的坡面或不同下垫面之间过渡时,由于局部坡度较大,径流过程趋向于汇聚收敛。准确区分水流流态是进行水量合理分配的前提,然而,目前研究领域对于城市地表水力梯度的陡缓特征没有明确的判断标准。
本文在UCA算法中设计了流态判断规则,提出流态判断的标准差阈值。该流态判断规则综合考虑了元胞尺寸与邻域内9个元胞高程(水位)值对流态的影响,可以作为未来研究中城市地表水力梯度陡缓特征的判断依据。采用UCA算法进行不同水量分配权重下的坡面流模拟试验,结果显示UCA算法适用于城市地表缓坡漫散流态模拟的最优水量分配权重pd=1.1,这与Freeman对缓坡漫散流态模拟的研究结论一致,说明UCA算法设计的流态判断规则具有一定的合理性。同时,在陡坡汇聚流态模拟的研究中,Qin等[8,16,19-20]认为在沟谷地形汇聚流动的水量分配权重pc=10较为合理,而UCA算法适用于城市地表陡坡汇聚流态模拟的最优水量分配权重pc=2.0,说明相比于天然流域,城市地形不会出现类似于沟谷地形中的汇聚流态,即pc取值不会过大。
元胞自动机可以通过定义简单的规则演绎复杂的动力系统,对于城市水文过程模拟具有独特的算法优势[12-13]。UCA算法模拟效果相对于传统流向算法更好,适用于分布式网格计算。未来研究可基于UCA算法开发适用于城市复杂地形变化的水文模型,为城市水利水务部门的洪涝预警、面源污染削减等提供更准确的信息。本文的不足之处在于缺乏实测资料,算法评价选择在4种具有代表性的人工数学曲面上开展,在实际应用过程仍有值得改进之处。未来研究可对真实城市地形展开模拟,并用实测汇流数据作为验证条件来改进算法。同时,地下管网汇流过程是城市径流的重要过程,后续研究可以考虑在元胞自动机模型中增加地下管网汇流模块,实现地表和地下管网汇流的耦合计算。
4 结 论
a.UCA算法中适用于城市陡坡汇聚流态和缓坡漫散流态模拟的最优水量分配权重取值分别为2.0和1.1,可为后续多流向算法的水量分配权重取值提供参考。
b.UCA算法在FMFD算法的基础上考虑了局部地形特征变化,采用水量分配权重随地表特征进行变化的方式处理水流多流向分配问题,其单位汇流面积模拟结果与理论值差异更小。
c.UCA算法兼顾了单流向与多流向算法的优势,既能模拟城市平坦地形上的缓坡漫散流,也能模拟城市水力梯度较大地形上的陡坡汇聚流,可为城市地表径流过程模拟提供更优的求解思路。

