关中平原极端降水时空变化及其与大气环流的关系

丁莹莹， 邱德勋， 吴常雪， 穆兴民,， 高 鹏,

（1.西北农林科技大学水土保持研究所，黄土高原土壤侵蚀与旱地农业国家重点实验室，陕西 杨凌 712100；2.中国科学院水利部水土保持研究所，陕西 杨凌 712100）

水循环是联系海洋与内陆实现水资源循环更新的重要物质循环之一，降水是水循环的四个基本环节中的重要一环。在全球气候变化和人类活动的影响下，水循环过程加剧，极端降水事件频发。极端降水事件虽是小概率事件［1］，但它具有较强的持续时间不确定性，持续多天的极端降水事件往往具有较大的致灾性［2］，易诱发山洪、泥石流和滑坡等地质灾害，严重威胁着人类的生命财产安全［3］。

目前，有关极端降水的研究集中在极端降水的时空变化规律、极端降水与大气环流的关系、极端降水事件模拟以及基于人工神经网络和机器学习的未来极端降水事件预测等方面［4-6］。研究的区域范围覆盖华南、西南和七大流域等。戴声佩等［7］基于华南地区1959—2016 年逐日实测降水资料分析了极端降水的时空变化特征，发现大尺度的大气环流对华南地区极端降水有显著影响。杜懿等［8］通过信号分析和机器学习方法建立BPNN、WANN、TSNN、SVM、ELM 降水量预测模型，得出除BPNN外，其他模型能理想的预测降雨量。罗志文等［9］基于地区线性矩法探究了陕西省极端降水时空变化特征，发现极端降水的分布特征与独特的地理位置有关。

关中平原因秦岭和陕北高原环绕，地理位置特殊，水汽输送过程受阻，水循环过程也相应发生变化。刘燕飞等［10］通过一次暴雨的数值模拟研究发现关中平原东部降水量低于西部，可能与秦岭的阻挡有关。白爱娟等［11］研究发现关中地区受副热带高压影响，暖湿气流不易通过季风环流到达欧亚大陆北部地区，导致陕西省冬春季少雨。大气环流异常是引起气候变化的直接原因，极端降水事件频发与大气环流异常有密切关系［12］。东西太平洋气压差变化影响风向从而影响大气环流、水汽传送，进而影响降水过程。其中反应大气环流的南方涛动（SOI）与厄尔尼诺现象（ENSO）的活跃程度息息相关，张冲等［13］研究发现关中地区1951—2008 年ENSO增强时，降水量下降。周旗等［5］对渭河极端降水进行上中下游对比分析，认为在20 世纪90 年代以前和2000 年以后，降水情况年际差异大，中游变化更为明显。关中平原是渭河冲积平原，地处渭河中游，对气候变化敏感［14］，且近年来西北地区强降水有增多趋势。但是关于大气环流影响关中地区极端降水的潜在机制尚不明确，因此有必要对该区域的极端降水与大气环流的关系做进一步研究，以期为关中平原水资源调配、工农业发展和洪水灾害防治提供理论支撑。

1 研究区概况

关中平原位于陕西中部，有13个气象站（图1），介于秦岭与渭北北山，所指为渭河冲积平原，西起宝鸡，东至潼关，包括宝鸡、咸阳、铜川、渭南和西安5 个地级市，地势西高东低，海拔约为325～800 m，面积约为3.4×104km2，属大陆性气候，年均温6～13 ℃，年降水量为500～800 mm，受季风气候影响降水主要集中在夏秋季6—9 月，多为短时暴雨。关中平原自然经济条件优越，人口密集，自古以来就是农业富庶之地，在全国区域经济发展中占据重要地位［15］。

2 数据与方法

2.1 数据来源

利用关中平原13 个气象站1957—2019 年逐日降水资料，分析近63 a 6 个极端降水指数的时空变化及其与大气环流的相关关系。各气象站逐日降水资料来源于中国气象科学数据共享服务网（http://data.cma.cn），部分缺测数据通过临近站点插补，利用RClimate 软件对降水数据进行质量和一致性检验，数据均表现良好。关中平原数字高程（DEM）数据来源于地理空间数据云（http://www.gscloud.cn/search），美国太空总署（NASA）和国防部国家测绘局（NIMA）联合测量的90 m分辨率数字高程数据产品。AMO（大西洋年际振荡指数）、AO（北极涛动指数）、NAO（北大西洋涛动指数）、NP（北太平洋遥相关指数）、PDO（太平洋年代际振荡指数）、WP（西太平洋指数）和SOI（南方涛动指数）等反映大气环流的指数数据来源于美国国家海洋和大气管理局地球系统研究实验室（https://psl.noaa.gov/data/climateindices/）。

2.2 研究方法

2.2.1 极端降水指数的选取 根据世界气象组织（World Meteorological Organization，WMO）以及气候学委员会（CCI）组建的气象监测专家组推荐的极端降水指标再结合关中平原的气候类型选取6个极端降水指数。这些降水指数分别能反映研究区域的降水量、降水日数和降水强度[6,16]（表1）。

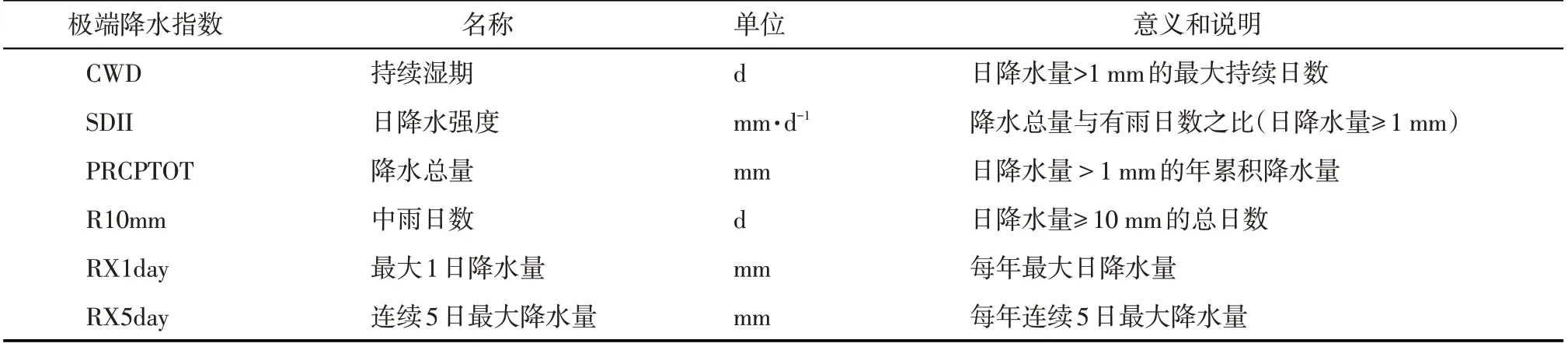
表1 极端降水指数及定义Tab.1 Extreme precipitation index and definition

2.2.2 一元线性回归 利用线性回归最小二乘法和10 a 滑动平均进行极端降水指数的时间变化趋势分析，线性回归方程的斜率为线性倾向率。线性倾向率为正值时，表明对应序列呈上升趋势；反之，呈下降趋势，线性倾向率的绝对值大小表示序列的变化程度［17］。非参数检验是不依赖于总体分布的数据分析方法，利用Mann-Kendall进行非参数检验，检验各个极端降水指数得到反映各指数变化显著性水平Z值。如果Z＞0，说明变量呈增加趋势；反之，说明序列呈减少趋势。当α=0.05 和α=0.01，Z值对应绝对值为1.96 和2.58，Z值的绝对值远远大于1.96 或2.58 时，表明序列增加或减少的趋势越显著［18］。

用一元线性回归极端降水指数的年际变化趋势：

运用最小二乘法对一元线性回归方程进行求解，过程如下：

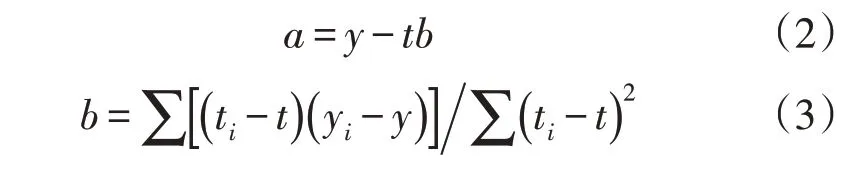
式中：y为极端降水指数；b为线性倾向率；t为时间序列。

利用Mann-Kendall 进行突变点检验，其原理如下：

得到的UFk、UBk曲线，如果UFk与UBk出现交点，且交点在临界线之内，那么交点就是突变开始的时间。UFk＞0 表示序列呈上升趋势，反之，呈下降趋势。UFk和UBk超出临界值时，表示变化趋势显著。

2.2.3 小波相干分析 小波相干来源于傅立叶相干，小波相干分析能通过交叉小波相干谱直观反映影响因子与径流的位相关系和局部相关程度［19］。图谱中锥形细线区域为有效谱值区，图中粗实线区表示通过了5%的显著性水平的置信区间，箭头所指方向反映了两时间序列的位相关系，箭头向右表示影响因子与径流之间同相位，两序列具有正相关关系；箭头向左，反之。箭头向下，表示影响因子变化超前径流变化90°（对应时间为3 个月）；箭头向下，表示影响因子变化落后径流变化90°，有效谱值区可避免边界效应及小波高频假信息［20-21］。

对于2 个时间序列X与Y之间的交叉小波功率谱（XWT）定义为［22］

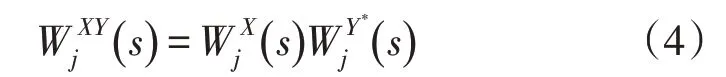
小波相干谱定义［21］如下

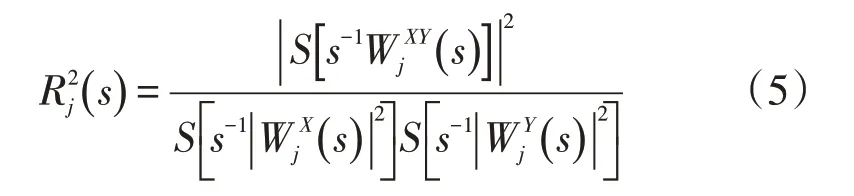
式中：S为平滑算子。

本文利用小波相干谱来分析极端降水指数与大气环流因子的局部相关程度。

3 结果与分析

3.1 极端降水的时空变化

3.1.1 时间变化 基于各气象站点逐日降水数据，利用泰森多边形法推求极端降水指数，并计算各极端降水指数在时间序列上的多年均值，分析关中平原极端降水指数63 a来的变化趋势（图2）。关中平原属暖温带半湿润气候区，总体来看，所有的极端降水指数变化趋势均不显著，除SDII以0.01 mm·d-1·(10a)-1速率增大外，其余均呈不显著的减少趋势。20 世纪90 年代以前和2000 年以后，通过10 a 滑动平均法所作趋势线可看出，极端降水指数表现出了往复的变化趋势，有微弱的往复变化特点，其中CWD 在90 年代以前呈下降趋势，2000—2009 年有较明显的上升趋势。其余极端降水指数以年际震荡为主。PRCRPTOT 以-5.528 mm·(10a)-1速率减少，多年平均值为513.36 mm，最小值为332.6 mm，出现在1997 年（表2）；RX1day 以-0.105 mm·(10a)-1的速率减少，RX5day 和CWD 分别以-0.096 mm·(10a)-1和-0.171 d·(10a)-1的速率下降。表征降水大小持续日数的R10mm 的线性倾向率为-0.005 d·(10a)-1，整体上呈不显著的下降趋势，波动性较大。经Mann-Kendall突变检验发现各极端降水指数且未发生显著性突变。

表2 极端降水指数特征值Tab.2 Characteristic values of extreme precipitation index

3.1.2 空间变化 依据13 个站点极端降水指数多年均值以及各站点的极端降水指数的线性倾向率，通过地学分析模块中的反距离权重法插值（IDW）得到关中平原各极端降水指数的空间分布及变化趋势（图3）。

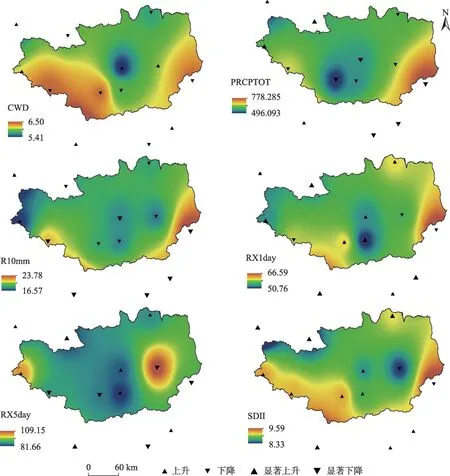
图3 极端降水指数空间变化趋势Fig.3 Spatial variation trend of extreme precipitation index

在空间分布上，极端降水呈现南高北低的分布规律，空间差异显著，各极端降水指数均呈现出自西南部佛坪站和东南部向西北部递减的趋势。关中南部佛坪站CWD 最大，为7.38 d，西部地区CWD较东北部较长，东南部CWD 最大值发生在华山站6.25 d。受气候地形等因素影响，PRCPTOT 自西南和东南向西北递减，中部降水较少，关中东南部华山站PRCPTOT 较大为783.45 mm，武功、西安站降水量相对较少，年均极端降水总量最大值发生在佛坪站，为910.53 mm，PRCPTOT最小值发生在关中平原西北部的崆峒站，为495.91 mm。R10mm 最大值发生在佛坪站，为27.57 d，最小值发生在崆峒站，为15.56 d。R10mm 呈现出由东南和西南向西北递减的趋势。西安站RX1day 最小为50.76 mm，RX1day最大值在佛坪站为75.97 mm。崆峒站RX5day 最小，为81.35 mm，RX1day的极大值发生在佛坪站，陇县站RX5day 最大，多年均值为165.2 mm；崆峒站多年平均SDII 最小，佛坪站SDII 多年平均值最大，为

10.25 mm·d-1。

在空间变化趋势上，69.2%的站点PRCPTOT 呈下降趋势，92.3%的站点R10mm 呈下降趋势（表3）。除商州、陇县站以外，其他站的CWD 都呈下降趋势；崆峒、长武、佛坪站和陇县站PRCPTOT均呈上升趋势，其他站均呈下降趋势，镇安站PRCPTOT 下降幅度最大，下降速率为18.7 mm·(10a)-1，其次是华山站，下降速率为14.35 mm·(10a)-1。除崆峒站R10mm以0.15 d·(10a)-1的速率上升外，其他站均呈下降趋势。宝鸡、华山和蒲城站RX1day 分别以-0.47 mm·(10a)-1、-0.51 mm·(10a)-1和-0.75 mm·(10a)-1的速率下降，其他站RX1day 均呈上升趋势，长武站RX1day 上升幅度最大，上升速率为3.59 mm·(10a)-1，佛坪和商州站RX1day 上升幅度相近。宝鸡、耀县、武功、华山、镇安、陇县和蒲城站RX5day均呈下降趋势，蒲城站下降趋势更显著，下降速率达-4.48 mm·(10a)-1，其他站RX5day 均呈上升趋势，长武站上升幅度最大，上升速率为5.45 mm·(10a)-1，其次是佛坪站，上升速率为2.48 mm·(10a)-1。耀县站SDII未发生显著性变化，除华山站和蒲城站SDII以-0.06 mm·d-1·(10a)-1和-0.073 mm·d-1·(10a)-1的速率减小外，其他站的SDII均呈增大趋势。除关中平原东南部外其他区域SDII均呈显著上升趋势，且关中平原西北部PRCPTOT 和SDII 呈增加趋势，CWD呈减少趋势，未来极端降水事件发生的可能性增大。

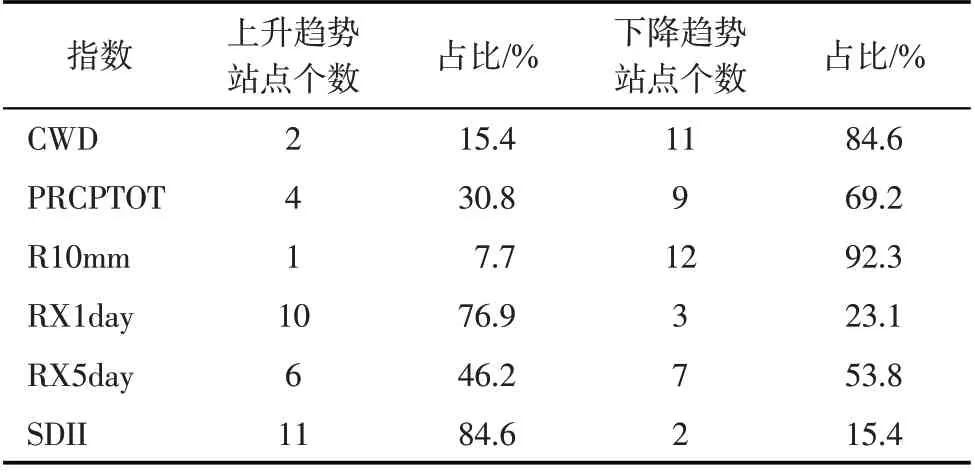
表3 极端降水指数空间变化趋势Tab.3 Statistical analysis of spatial variation trend of extreme precipitation index

3.2 各极端降水指数变化的一致性

除CWD以外，其他极端降水指数之间都存在显著正相关性，相关系数在0.29～0.8 之间，且通过了0.05的显著性水平检验。R10mm、RX5day和SDII与PRCPTOT 的相关性均通过了0.01 的显著性水平检验，且与PRCPTOT 表现出良好的相关性，表明所选取的极端降水指数对年降水总量具有很好的指示作用，极端降水指数的增加或减少能反映出降水量的增加或减少（表4）。

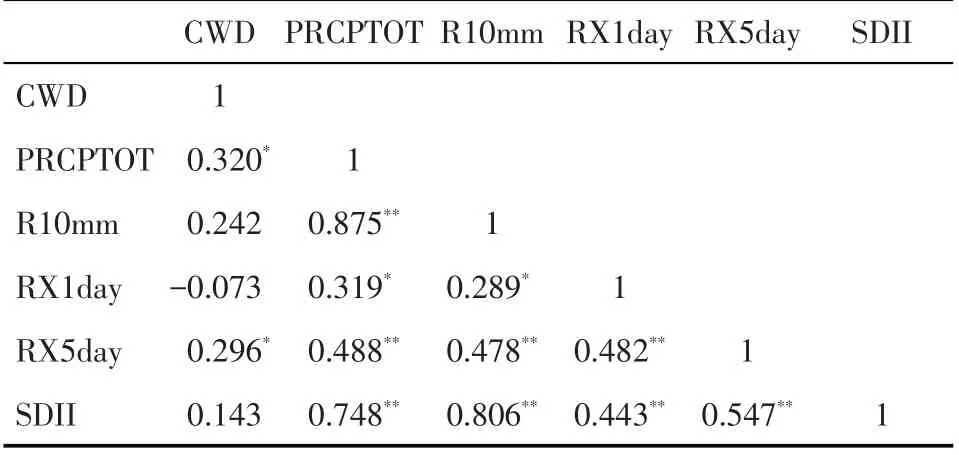
表4 极端降水指数相关系数Tab.4 Correlation coefficient of extreme precipitation index

3.3 极端降水与大气环流的关系

3.3.1 Pearson 相关性分析 选取1957—2019 年间的反应大气环流的AMO、AO、NAO、NP、PDO、WP和SOI 指数与同时间序列的6 个极端降水指数进行不同季度尺度相关分析发现除RX5day 以外，关中平原各极端降水指数都一定程度上受SOI、NP 和PDO等反映大气环流的因子的影响。SOI与极端降水关系密切。在99%的显著性水平下，4—12月SOI因子都与R10mm呈显著正相关。4—12月的SOI因子与PRCPTOT 呈显著正相关（P＜0.01），且SOI 越大，年均PRCPTOT 减少趋势越显著。NP 与SDII 在1—3月呈显著负相关（P＜0.05），与RX1day 和SDII 在10—12 月呈显著正相关（P＜0.05）。PDO 与RX1day在7—9月呈显著负相关，显著性水平为95%（表5）。

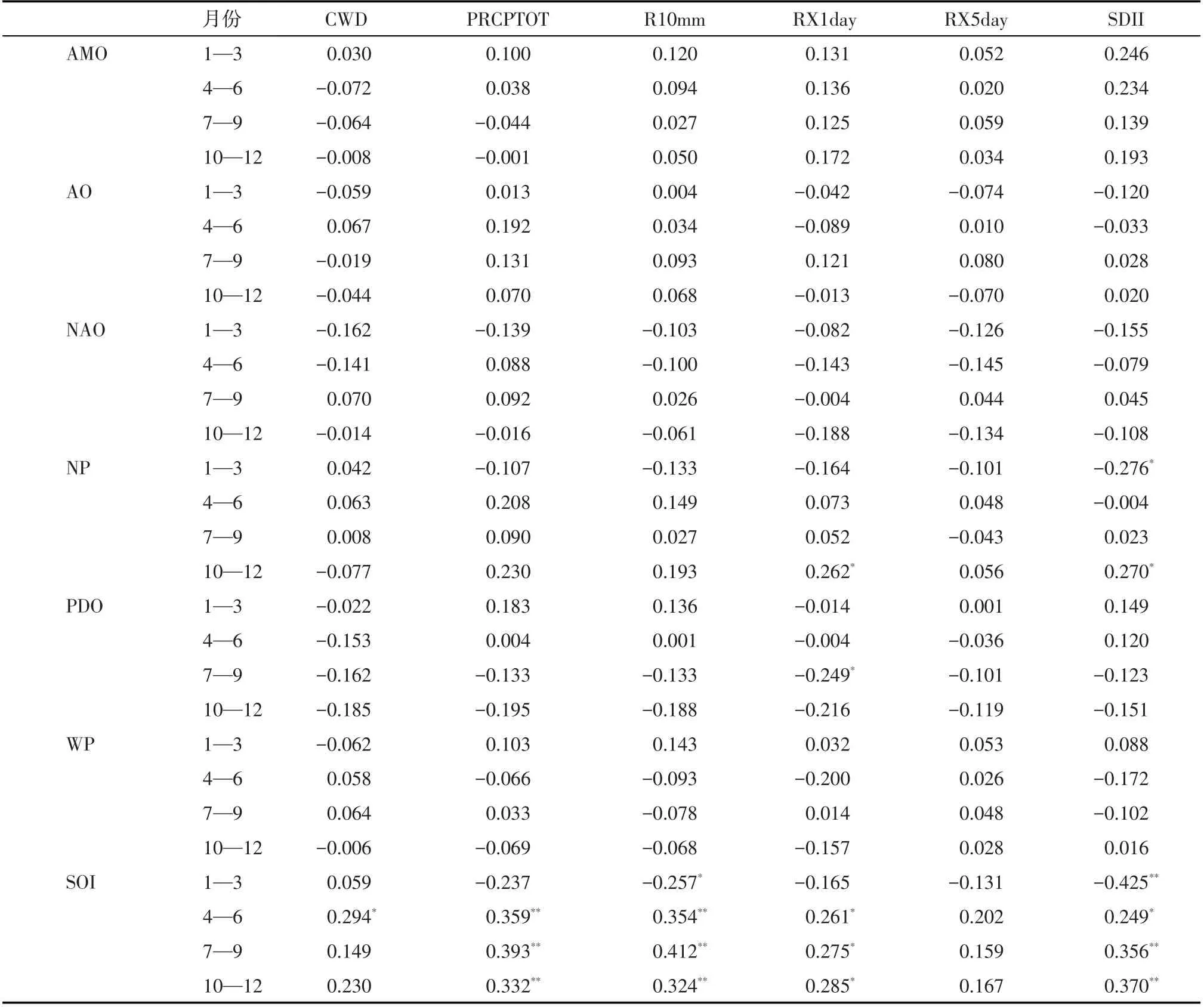
表5 极端降水指数与大气环流因子的相关系数Tab.5 Correlation coefficients between extreme precipitation indices and atmospheric general circulation factors

3.3.2 极端降水指数与SOI 的关联分析 使用小波相干分析法进一步探究SOI 与PRCPTOT、R10mm、SDII和CWD在低能量区的相互关系（图4）。SOI与CWD 在1965—1968 年相位差约为150°存在相关系数约为0.83 的负相关性，具有2～4 a 的共振周期。R10mm和SOI在1980—1989年间正相关程度较大，周期在5～6 a 之间出现显著共振周期，局部相关系数达0.8 以上。在1973—1988 年之间SOI 与PRCPTOT 存在相关系数可达0.85 的显著正相关性，具有准5 a的共振周期。SOI与R10mm在1980—1985年存在4～5 a 的共振周期,位相差约为30°相关系数可达0.9，通过了95%的置信度检验。在1980—1985年，SOI与SDII也存在4～5 a的共振周期且二者呈正相关，位相差约为60°，局部相关系数可达0.82。反映大气环流的SOI对各极端降水指数的周期性影响具有一致性。

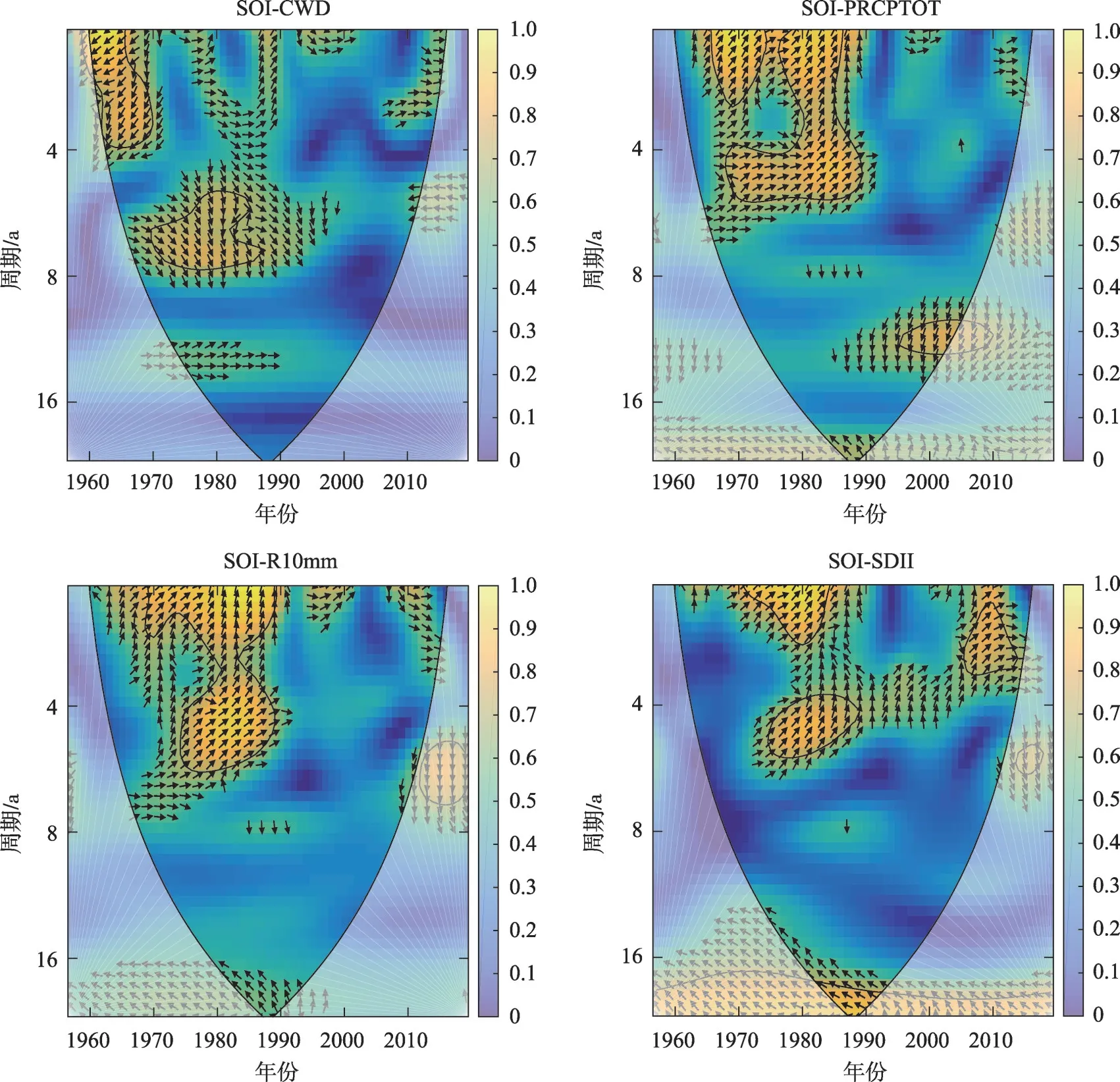
图4 大气环流因子与极端降水指数的小波相干谱Fig.4 Wavelet coherence spectrum of atmospheric general circulation factors and extreme precipitation indices

4 结论

（1）在时间上，除SDII 呈上升趋势外，CWD、PRCPTOT、R10mm、RX1day 和RX5day 均呈不显著的下降趋势。PRCPTOT 下降速度最快，下降速率为-5.528 mm·(10a)-1，且无突变点。

（2）在空间上，关中平原各极端降水指数南高北低。关中平原极端降水指数最大值主要发生在东南部和西南部地区，西北部易发生集中性的极端降水。其中位于关中平原南部的佛坪站CWD、PRCPTOT、R10mm、RX1day和SDII最大。

（3）在所选择的反映大气环流的因子中，SOI对极端降水有显著影响。SOI 与PRCPTOT 存在准5 a的共振周期。SOI与极端降水指数具有显著局部正相关性，SOI越大，关中平原越易出现少雨现象。