基于蒸发皿实验的大气水汽氢氧稳定同位素模拟

雷世军， 王圣杰， 朱小凡， 张明军

（1.西北师范大学地理与环境科学学院，甘肃 兰州 730070；2.甘肃省绿洲资源环境与可持续发展重点实验室，甘肃 兰州 730070；3.中国科学院西北生态环境资源研究院，甘肃 兰州 730000）

水体中的氢氧稳定同位素（2H 和18O）是研究水文循环和古气候信息重建的天然示踪剂［1-3］。大气水汽是形成降水的必要物质条件，水汽中氢氧稳定同位素也相应地蕴含着蒸发、输送、凝结等环境信息［4-7］。相比于降水，大气水汽同位素能为水汽过程诊断提供直接的证据，其优势表现在时间、空间等多方面［5］。水汽同位素可以实现全天候的连续监测［8-10］，不像降水同位素那样仅能够代表降水时段的特征，从而得到时间序列连续的大气水分信息，这在降水匮乏的干旱半干旱区显得十分重要。结合浮空艇、无人机和卫星遥感等手段，水汽同位素还可以实现三维空间覆盖，相比之下地面降水同位素对垂直方向上的水汽过程刻画则具有其局限性［11-12］。此外，雨滴在不饱和空气中的下落过程可能会发生云下二次蒸发，影响降水同位素的时空特征［13-16］，而对水汽同位素的监测能够在一定程度上弱化云下蒸发导致的降水同位素信息失真问题。

早期大气水汽氢氧稳定同位素研究主要以低温冷凝空气获得液态水样进行分析，即低温冷阱法，该方法对实验操作具有较高的要求，往往难以精细表征大气水汽同位素在时间和空间上的变化，特别是在水汽含量低的情况下水汽液化比较耗时费力［17-19］。随着激光光谱技术的发展，实时在线监测大气水汽的氢氧稳定同位素数据成为可能［20-22］。激光光谱技术克服了低温冷阱法在连续测量上的局限性，但由于成本相对较高，无法广泛地开展监测工作。当不能直接监测大气水汽同位素时，可利用Craig-Gordon线性阻力模型［23］和水体同位素质量平衡方法来模拟［24-27］，并结合实测水汽同位素数据加以验证。

为了研究基于Craig-Gordon 线性阻力模型和同位素质量平衡的方法在计算干旱半干旱区大气水汽氢氧稳定同位素时的可靠性，本文基于蒸发皿实验模拟了甘肃兰州大气水汽氢氧稳定同位素，并结合在线水汽同位素分析仪的同步监测记录，评估了蒸发皿实验模拟结果的可靠性，旨在为获取连续大气水汽氢氧稳定同位素数据提供了一种相对简单的方法。

1 材料与方法

1.1 蒸发皿实验

试验地位于甘肃省兰州市安宁区西北师范大学新校区（103°44′E，36°6′N），地处季风边缘区，属于半干旱气候，气温年较差大，降水多集中在夏季。蒸发皿实验于2019 年9 月25 日—11 月1 日进行，实验期间的平均气温为14.4 ℃，平均相对湿度为46%。选用长420 mm、宽220 mm、高200 mm 的长方体透明玻璃水箱作为蒸发皿，放置于开阔、通风良好的场地。当有降雨发生时，在蒸发皿上方0.5 m高度处用透光塑料薄膜遮盖，防止降雨进入蒸发皿，降雨结束后及时移除。实验初始将当地自来水注入蒸发皿中，每日同一时间用钢尺测量水位并记录，然后充分搅拌水体后用注射器抽取1 mL的水体样本储存在玻璃瓶中密封冷藏保存。为了减少取样造成水量损失对结果的影响，在上述蒸发皿旁0.5 m 处设置一个同样大小和材质的蒸发皿作为补给箱，在初始条件下装入同量的自来水同时进行蒸发，每日抽取1 mL的水体补充到用于收集剩余水体的蒸发皿中。实验过程中实时监测大气温度和相对湿度并记录。抽取的逐日蒸发剩余水体采用加拿大ABB-Los Gatos Research 公司研发的T-LWIA-45-EP型液态水同位素分析仪进行氢氧稳定同位素测定，δ18O 的测量误差小于±0.3‰，δ2H 的测量误差小于±1.0‰。

氢氧稳定同位素比率用相对于维也纳标准平均海洋水（V-SMOW）的千分差表示，公式如下：

式中：Rsample表示蒸发水体样本的同位素比率；RV-SMOW表示维也纳标准平均海洋水的同位素比率。

1.2 大气水汽同位素测量

大气水汽氢氧稳定同位素的监测采用加拿大ABB-Los Gatos Research 公司研发的超便携式水汽同位素分析仪（Ultraportable Water Vapor Isotope Analyzer，型号UWVIA-915），与蒸发皿实验同期进行。该分析仪基于离轴集成腔输出光谱技术，可以通过测定不同氢氧稳定同位素对于特定波长红外波的吸收强度来计算其浓度，采样频率可达秒级。本研究中δ18O 的测量精度为±0.05‰，δ2H 的测量精度为±0.2‰。仪器通过水汽校准源系统（Water Vapor Isotope Standard Source，简称WVISS）产生标样水汽，测量过程中将标样水汽每浓度梯度开始时和结束时的测量值删除，取每梯度中间较为稳定的同位素值作为该梯度的标样水汽同位素值以减轻记忆效应对实验结果的影响。在测量大气水汽同位素时，将前10 min 的测量值删除，至大气水汽浓度稳定以后再进行测量［28］。浓度效应的校准参考了Rambo 等［29］的方法，标样水中同位素和气化后的标样水汽中的同位素一致［20,30］，可通过T-LWIA-45-EP型液态水同位素分析仪测定后作为标样水汽的真值，将该测量真值与水汽同位素分析仪得到的标样水汽同位素求差，用水汽浓度和差值进行二项式曲线拟合，获得对应水汽浓度下的测量误差值，从而对水汽同位素进行浓度效应校准。

1.3 基于蒸发皿实验的模拟计算

Craig-Gordon 线性阻力模型［23］被广泛应用在蒸发水汽同位素的估算中，方法如下：

式中：δE表示蒸发水汽的同位素比率；δL表示蒸发剩余水体的同位素比率；δA表示大气水汽同位素比率；h是空气的相对湿度；α*是平衡分馏系数，可以通过Horita等［31］的公式得到；ε*是平衡分馏因子，可由ε*=α*-1得到；εK是动力分馏因子，氧和氢的同位素动力分馏因子分别为εK=14.2(1-h)和εK=12.5(1-h)；ε是总分馏因子，ε=ε*+εK［32］。Gibson等［25］认为蒸发水体的同位素取决于大气水汽的同位素，对于一个混合良好的水体在自然蒸发条件下而言，在dt的时间间隔下，水量的变化为dV，则质量平衡方程为：

同位素质量平衡方程为：

式中：V是水体的水量；I是水的流入量；δI是流入水体的同位素组成；Q是流出量；δQ是流出水体的同位素比率；E是蒸发量；δE是蒸发水体的同位素比率。将式（2）中δE代入式（4）可得：

此式为同位素质量平衡方程的通用公式。在本实验中，蒸发皿作为蒸发水体的容器，体积固定，不存在流入和流出的情况，蒸发皿中水量只受到自然条件下的蒸发影响而减小。将V0当作蒸发初始时的水量，定义f=V/V0为蒸发程度的指标，式（4）可改写为：

将式（2）和式（6）合并整理可得：

随着蒸发的进行，水体中同位素δL逐渐接近1个固定值，称之为同位素的“稳态”，即式（7）中δ*，其中是一个几乎完全取决于相对湿度的参数［33］。

将式（7）和式（8）整理后可得：

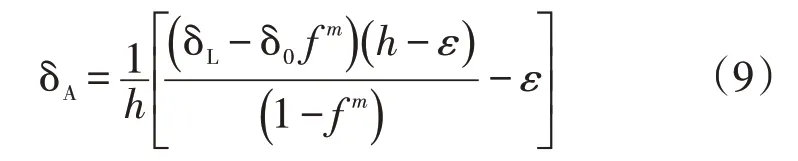
该式即为通过蒸发皿实验计算大气水汽同位素的计算式。

对于大气水汽同位素的模拟精度采用均方根误差（Root Mean Square Error，RMSE）、平均绝对误差（Mean Absolute Error，MAE）和平均偏差（Mean Bias Error，MBE）进行评估。

式中：δA表示实测的大气水汽同位素比率；δA-PD表示模拟的大气水汽同位素比率。

2 结果与分析

2.1 氢氧稳定同位素的时间变化

蒸发水体的稳定同位素初始值分别为δ18O=-9.50‰和δ2H=-65.60‰，随着蒸发皿中水体的蒸发损失，剩余水体中稳定同位素逐渐富集，δ18O 从-9.50‰增大至21.08‰（图1a），δ2H从-65.60‰增大至50.25‰（图1b）。这符合蒸发剩余水体中同位素的基本变化规律［34-35］。Devi等［27］在印度的蒸发皿实验中，剩余水体中δ18O从-6.30‰增大至13.63‰，δ2H从-43.48‰增大至46.50‰，与本研究中水体同位素的变化范围比较接近，但实验期间平均温度（26.5 ℃）和相对湿度（49%）比本研究更高。

图1 2019年9—11月蒸发皿实验期间实测蒸发剩余水体（δL）、模拟蒸发水汽（δE）、模拟大气水汽（δA-PD）和实测大气水汽（δA）中δ18O（a）和δ2H（b）的日变化Fig.1 Daily variations of δ18O(a)and δ2H(b)in measured remaining pan water(δL),simulated evaporation water vapor(δE),simulated atmospheric water vapor(δA-PD),measured atmospheric water vapor(δA)during evaporation pan experiment from September to November 2019

在实验前期，蒸发剩余水体同位素变化相对较为平缓，而在实验末期蒸发皿中水量减少，水体更易受到气象条件变化的影响，同位素的蒸发富集速率略微增加。伴随着蒸发过程，模拟的蒸发水汽同位素也逐渐富集，表现出和蒸发剩余水体类似的规律，δ18O 从-39.35‰逐渐富 集 到13.73‰，δ2H 从-166.8‰逐渐富集到18.43‰，但在整体上低于剩余水体中的稳定同位素（图1）。实测大气水汽中的δ18O在实验期间的变化范围在-23.4‰～-13.86‰之间，平均值为-18.36‰；δ2H 的变化范围在-154.79‰～-90.11‰之间，平均值为-122.69‰。基于蒸发皿实验模拟的大气水汽中δ18O 的变化范围在-31.02‰～-7.03‰之 间，平 均 值 为-18.56‰，δ2H 则 在-217.74‰～-113.22‰之间，平均值为-153.09‰。从时间序列来看，模拟大气水汽δ18O 在实验前期波动较小并与直接测量得到的大气水汽δ18O表现出较好的一致性，在实验末期模拟大气水汽δ18O 的波动相对较大。总体来说，在观测时段内，模拟的大气水汽同位素和实测的大气水汽同位素变化趋势基本一致。

2.2 实测值与模拟值的对比

根据蒸发剩余水体中的氢氧稳定同位素比率，可以得到δ18O 和δ2H 的线性关系，即蒸发线（δ2H=3.76δ18O-28.54，图2）。在自然条件下的蒸发过程中，水体中同位素的变化不仅受到大气温度和相对湿度的影响，也受到大气水汽中同位素的影响［35］，蒸发线的斜率反映了蒸发过程中非平衡分馏程度的强弱，斜率越小表明非平衡分馏越强。本次实验的蒸发线斜率（3.76）符合Gat［36］提出的蒸发线斜率通常在3.5～6 之间的观点，表明水体受到了强烈的非平衡分馏作用使得蒸发线的斜率远低于全球降水线的斜率。

图2 2019年9—11月蒸发皿实验期间模拟大气水汽（δA-PD）、实测大气水汽（δA）和蒸发剩余水体（δL）中δ18O和δ2H的关系Fig.2 Correlations between δ18O and δ2H in simulated atmospheric water vapor(δA-PD),measured atmospheric water vapor(δA)and remaining pan water(δL)during evaporation pan experiment from September to November 2019

相较于实测的大气水汽同位素，模拟所得的大气水汽中δ2H 在整体上要低于实际测量的δ2H（图1b），因此模拟值分布在实测值的下方（图2）。整体上看，不论实测还是模拟的大气水汽同位素都分布在全球大气水线附近，与Gat［37］的观点基本一致。但是本研究的实验地点相对湿度较低（46%），同时蒸发强烈，蒸发皿的日均实际蒸发量为3.3 mm，强烈的动力作用使得模拟和实测的大气水汽线的斜率均低于全球大气水线的斜率，同时蒸发皿水体的体积相较于一般的自然湖泊等地表水体偏小，蒸发模拟的过程更易受到环境因子的影响，使模拟得到的大气水汽线的斜率更低。

2.3 模型敏感性分析

将相对湿度、气温、蒸发剩余比和蒸发剩余水体同位素组成等参数进行敏感性分析（图3）。利用改变参数后模拟得出的大气水汽同位素与未改变参数模拟得出的大气水汽同位素的偏差来体现该参数的敏感性，偏差越大，表明该参数对模型的敏感性越强。本研究中，相对湿度的变化对于模拟结果的影响比较显著，当相对湿度降低时2σ（σ，标准差）时，偏差为7.65‰，而当相对湿度增加2σ时，偏差为3.87‰。相对湿度降低产生的影响大于相对湿度增加时产生的影响（图3a）。非平衡条件下的动力分馏与相对湿度具有很高的相关性［32,38］，当相对湿度降低时，动力作用加强使得蒸发朝着更加不平衡的方向发展，模拟的结果也出现较大的偏差。

在同等标准差变化下，温度对于该模型的影响相较于相对湿度要小，当温度变化2倍标准差时，模拟结果δ18O偏差在3‰以内，对于模拟准确性的影响相对较小（图3b）。在图3c 中，蒸发剩余比f减小和增大时，δ18O 偏差的变化幅度不同，由于f增加后不能超过1，所以选择了0.3倍标准差作为上限，在f增加0.3倍标准差以后，偏差增加的幅度也要大于f减小0.3倍标准差产生的偏差。剩余水体中同位素富集和贫化程度对模型的影响相对比较对称（图3d）。

图3 2019年9—11月蒸发皿实验期间模拟大气水汽δ18O在不同相对湿度（a）、温度（b）、蒸发剩余比（c）和蒸发剩余水体δ18O（d）条件下的敏感性分析Fig.3 Sensitivity analysis of simulated δ18O in atmospheric water vapor under various conditions of relative humidity(a),temperature(b),remaining ratio(c)and δ18O in remaining pan water(d)during evaporation pan experiment from September to November 2019

2.4 模拟可靠度评估

在本次实验中，对于δ18O 而言，RMSE 为4.5‰，MAE为3.2‰，MBE为0.03‰；对于δ2H而言，RMSE为38.1‰，MAE 为28.3‰，MBE 为28.3‰。Gibson 等［25］在加拿大北方的实验结果与本实验相符，在温度和相对湿度已知的情况下，利用蒸发皿实验可以得到较为准确的大气水汽同位素组成，这在降水稀少的地区具有重要的价值。类似的结论可见于Devi等［27］和Vallet-Coulomb等［26］的实验。

将实测水汽δ18O与模拟水汽δ18O的差值定义为模拟残差，δ18O的模拟残差值在-8‰～16‰之间，δ2H的模拟残差值在0‰～120‰之间。对模拟残差与各实验要素进行相关分析发现，温度与δ18O 的模拟残差之间的相关性不明显（R2=0.08）且未通过显著性检验（P＞0.05），温度不是引起模拟残差的主要原因（图4a）。而相对湿度与δ18O的模拟残差之间的相关性较强（R2=0.43）且通过了显著性检验（P＜0.01），两者之间具有负相关性（图4b）。相对湿度在40%以上时，δ18O的模拟残差数据点分布较为集中，而在相对湿度小于40%时模拟残差的数据点分布则更加离散，δ18O 模拟残差的极大值也出现在相对湿度小于40%的这一区间内，且对应了相对湿度的最小值。在低相对湿度的情况下，水体在蒸发过程中会经历更强烈的非平衡分馏过程，使得模拟结果出现较大的偏差。水汽压与δ18O 模拟残差呈负相关，相关性低于相对湿度和δ18O 模拟残差的相关性，数据点的分布也较为分散（图4e）。f与δ18O 模拟残差呈负相关（R2=0.39），在f＜0.3以后，δ18O的模拟残差值分布较为离散且出现了极大值和极小值，而在0.3＜f＜0.8 的部分，δ18O 模拟残差的分布比较集中，多在0‰附近（图4c）。f较小时表明蒸发剩余水体较少，易受到水体和大气之间同位素交换作用的影响，进而影响蒸发皿实验的结果。蒸发剩余水体δ18O 与δ18O 模拟残差具有一定的相关性（R2=0.37），在实验前期，蒸发剩余水体中同位素的升高，模拟残差从负值逐渐过渡到正值，但总体仍比较接近0。随着蒸发剩余水体δ18O大于8‰以后，模拟残差的分布变得更加离散（图4d）。在蒸发实验的后期，蒸发皿中水量减少后更易受到周围环境变化的影响，使得蒸发过程变得不稳定。同时，在蒸发后期，蒸发皿中的水体中重同位素已经变得相对富集，实验后期δ18O的模拟残差较大且较为分散。气压与δ18O 的模拟残差之间则没有表现出明显的相关性（R2=0.001）（图4f）。

δ2H 的模拟残差与各要素间的相关关系如图5所示，整体上与图4 中δ18O 的结果类似，但δ2H 的模拟残差在数值上要大于δ18O的模拟残差。此外，δ2H的模拟残差与湿度（R2=0.51），水汽压（R2=0.53）、蒸发剩余比（R2=0.52）和蒸发剩余水体δ2H（R2=0.61）的相关性要强于δ18O的模拟残差与上述要素间的相关性。在湿度低于40%和f＜0.3以及蒸发剩余水体中同位素富集以后，δ2H 的模拟残差均出现了较大的离散，但在相对湿度高于40%和0.3＜f＜0.8 以及蒸发实验前期，δ2H 的模拟残差与上述三要素则体现出较好的相关性。总体来说，相对湿度、蒸发剩余比和蒸发剩余水体中的氢氧同位素三者都与δ18O和δ2H的模拟残差存在明显的联系。

3 结论

本研究基于同位素质量平衡和Craig-Gordon 线性阻力模型设计了蒸发皿蒸发实验，模拟了与蒸发过程同期的大气水汽同位素组成，结合实际监测的大气水汽同位素数据，对该模型模拟的可靠性做了评估，得出了以下结论：

（1）在实验期间内，基于蒸发皿实验模拟的大气水汽中δ18O 与实际测量的大气水汽中δ18O 相比，RMSE 为4.49‰，MAE 为3.23‰，MBE 为0.03‰，模拟得到的大气水汽同位素变化可以反映出大气水汽同位素的变化。

（2）通过对模型的敏感性分析发现，在同等标准差变化下，温度对于该模型的影响相较于相对湿度要小。蒸发剩余比减小和增大时，δ18O 偏差的变化幅度不同，蒸发剩余比增大时结果更加敏感。

（3）相对湿度、蒸发剩余比和剩余水体的同位素值都与水汽δ18O 和δ2H 的模拟残差存在联系。当相对湿度低于40%时，模拟残差的分布更加离散。在实验末期蒸发剩余比减小以后，模拟残差相较于实验前期而言更大，较少的水量和蒸发剩余水体中相对富集的氢氧稳定同位素对应着较大的水汽同位素模拟残差。