基于Vpython的简谐振动合成可视化研究
何云存
(湖北大学物理与电子科学学院 湖北 武汉 430062)
任 涛
(武汉电力职业技术学院输配电工程系 湖北 武汉 430074)
1 引言
振动,在大学物理课程中有着承上启下的地位.上承力学,质点受线性回复力时,根据牛顿第二定律求解动力学方程,可得质点的运动方程呈三角函数形式,运动形式为简谐振动;下接波动以及光学,波动即是质点振动状态的传播,振动的合成是波叠加,以及光的干涉衍射现象的理论基础.一维简谐振动的合成使用旋转矢量法很好理解,二维和三维简谐振动的合成较一维复杂得多,对学生的空间想象能力要求较高,传统教学中往往只讲解一维简谐振动的合成.为了帮助学生建立完整的知识体系,使用形象直观的方法展现二维三维简谐振动的合成是有必要的.
计算机技术的日益发展,使物理教学更具生动多样性,能帮助学生理解抽象的物理问题,同时激发学生的学习兴趣[1].开源免费,语法简单的Python编程语言近年来不仅被广泛用于金融工程、科学研究,而且被用于辅助教学.Python拥有很多功能强大的第三方库,Vpython是一个三维图形库,可用于模拟仿真物体的运动[2].本文使用Vpython将二维三维简谐振动的合成可视化,当分振动的频率满足整数比值时,可形成稳定封闭的李萨如图形,该方法有助于学生理解简谐振动合成的原理以及性质.
2 简谐振动的合成
2.1 二维简谐振动的合成
两个分振动的振动方向分别沿x轴、y轴,分振动的方程形式为
x=A1cos(ω1t+φ1)
y=A2cos(ω2t+φ2)
其中A,ω,φ分别表示振幅、角频率、初相位.首先考虑分振动频率相同的情况,使用Vpython编程,代码如下:
#第一部分:调入3D模块Vpython,建立画布和坐标轴
from vpython import *
s1=canvas(width=1000,height=1000,x=0,y=0,background=color.white)
x = arrow(pos=vector(0,0,0),axis=vector(6,0,0),shaftwidth=0.1,color=color.black)
x_text=label(pos=vector(6.5,0,0),text="x",height=30,opacity=0,box=0)
y = arrow(pos=vector(0,0,0),axis=vector(0,6,0),shaftwidth=0.1,color=color.black)
y_text=label(pos=vector(0,6.7,0),text="y",height=30,opacity=0,box=0)
#第二部分:设定初始条件,建立一个蓝色小球作为振动物体
A1=4
A2=5
w1=pi
w2=pi
phi1=0
phi2=pi/3
t=0
dt=0.001
ball = sphere(pos=vector(A1*cos(phi1), A2*cos(phi2), 0), radius=0.5, color=color.blue,
make_trail=True)
#第三部分:循环体实现动态模拟
while True:
rate(500)
phi1=phi1+w1*dt
ball.pos.x=A1*cos(phi1)
phi2=phi2+w2*dt
ball.pos.y=A2*cos(phi2)
t=t+dt
第三部分是程序的核心部分,程序运行结果如图1所示,可以看到小球沿着椭圆轨道顺时针方向运动,若交换两个分振动的初始相位值,可看到小球轨迹不变,但是运动方向变成逆时针.当振幅、频率固定时,相位差决定轨迹的形状.

图1 同频率的二维简谐振动合成
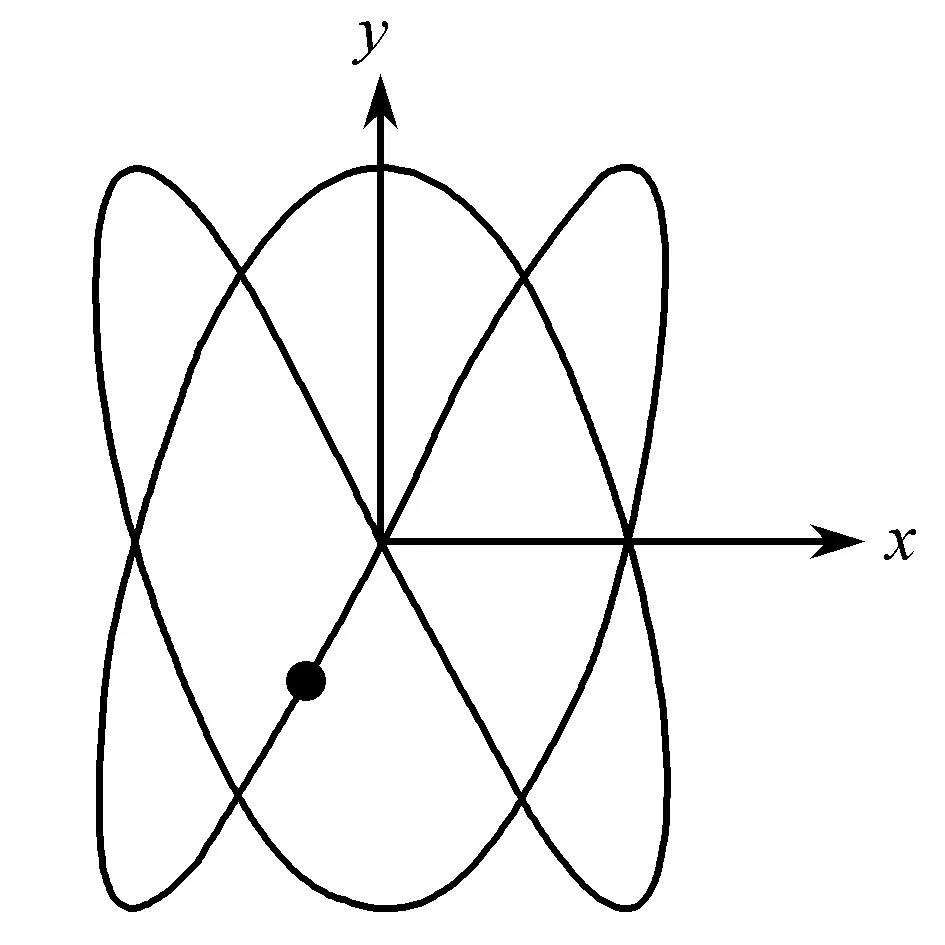
若分振动的频率不同,但是具有简单的整数比值,可形成稳定封闭的李萨如图形.李萨如图形与x轴、y轴的切点数目之比,与分频率之比呈反比.通过修改代码中分振动的频率以及初相位,我们得到几组不同的李萨如图形.
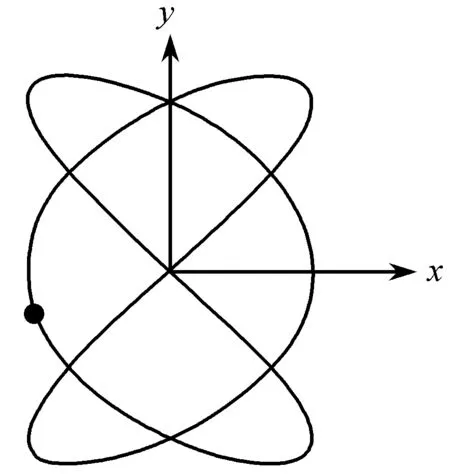
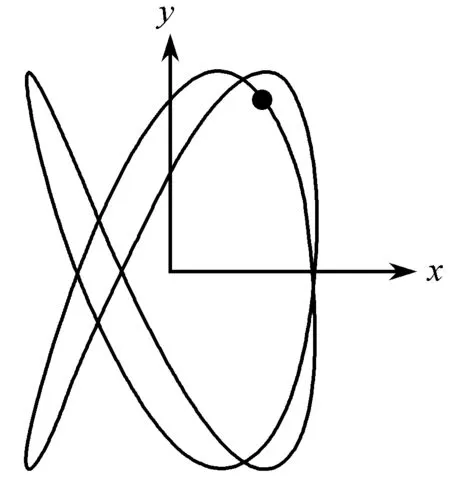
在图2中,(a)、(b)分振动的初相位相同,初相位差相同,x轴、y轴分频率之比分别是2∶3和3∶2,显然频率之比对轨迹形状有影响.图2(a)闭合曲线沿x轴切点数目3,沿y轴切点数目为2,图2(b)沿x轴切点数目2,沿y轴切点数目3,验证了切点数目之比与分频率之比呈反比的结论.

(b)

(a)
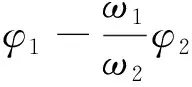



2.2 三维简谐振动的合成
振动方向相互正交的3个分振动频率满足整数比时,质点在空间中的运动轨迹呈三维李萨如图形.分振动的方程形式为
x=A1cos(ω1t+φ1)
y=A2cos(ω2t+φ2)
z=A3cos(ω3t+φ3)
此处以
A1=A2=A3=5
为例,分振动频率之比
ω1∶ω2∶ω3=1∶2∶3
三维振动合成的可视化需要在程序第一部分加上摄像机位置和角度的设定,即给定一个观察3D运动的视角.使用代码s1.camera.pos=vector(20,20,20)表示摄像机位置在x=20,y=20,z=20的空间点处,s1.camera.axis=vector(-20,-20,-20)表示摄像机方位正对着坐标原点.第二部分加入第三个分振动的初始信息,第三部分循环体中加入质点z轴坐标的计算公式ball.pos.z=A3*cos(phi3),运行得到对应视角下的三维李萨如图形,如图5所示.
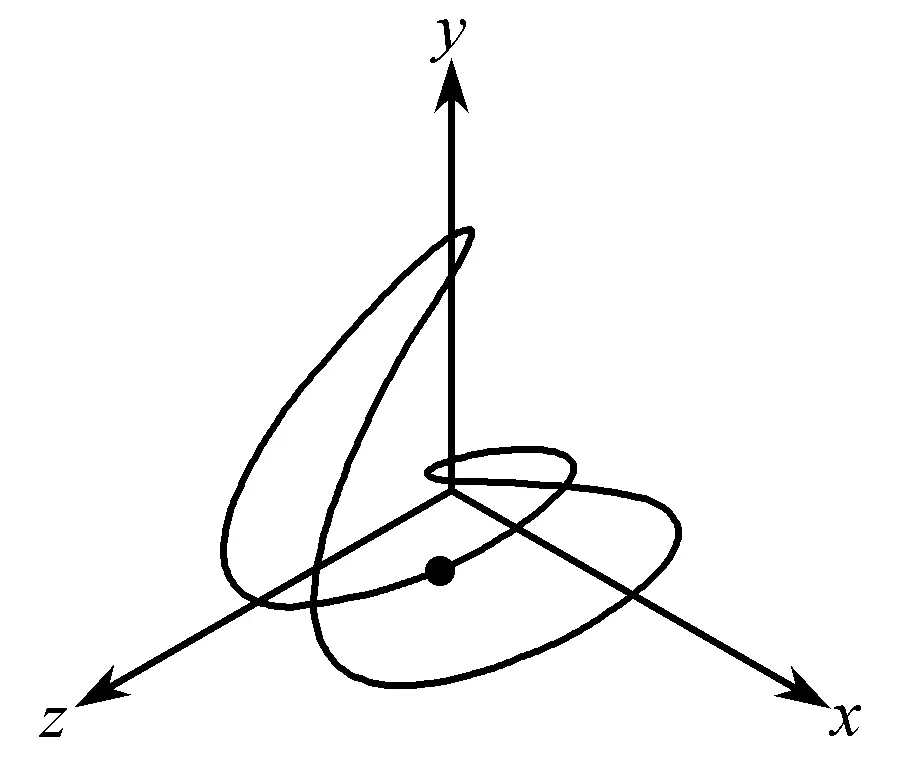
图5 三维简谐振动的合成
在Vpython模块下,我们可以身临其境般进入到三维空间任意位置观察质点的运动,只需改变摄像机位置和方向的设定,修改代码s1.camera.pos=vector(-20,20,20),s1.camera.axis=vector(20,
-20,-20),表示摄像机的位置和角度与第一次设定关于yz平面对称,此时看到的轨迹如图6所示.

图6 变换视角的三维简谐振动合成图
为了方便观察三维李萨如图形与xy平面、xz平面、yz平面的切点数目Nxy,Nxz,Nyz,我们可以站在y轴向下观察立体曲线在xz平面的投影图,站在z轴向下观察立体曲线在xy平面的投影图,如图7所示.
从图中看到曲线与xy平面的切点数目Nxy=3,与xz平面的切点数目Nxz=2,与yz平面的切点数目Nyz=1.平面图中沿x轴切点看似不在一条直线上,这是由于摄像机向下俯视,切点高度不一样所导致的视觉效果.与二维李萨如图形特点一致,各方向切点数目之比由频率之比决定,即
Nyz∶Nxz∶Nxy=ω1∶ω2∶ω3
3 总结
本文使用Python编程语言框架下的3D图形库Vpython,对二维、三维简谐振动的合成进行了可视化模拟,探讨了李萨如图形的特点,特别是对三维李萨如图形的模拟,解决了平面思维的困难,将质点的运动过程形象直观地呈现出来,有益于学生更加全面深刻地理解振动现象.Python语言简单易学,功能强大,除了可视化模拟,还可用于各种物理问题中的数值计算、建模分析等,是我们学习物理课程以及科研探索的现代化手段.

