基于改进Spark技术的高维数据增量式聚类算法

刘仁芬，杨凤丽，王 霞

(石家庄铁道大学四方学院，河北 石家庄051132)

1 引言

高维数据包含多种属性，例如空间位置信息、多物理参量、多时次数据、医疗数据等，也可将其理解为维度超过2的数据。该类数据已经称为当下生活中经常使用的一种数据[1]，但是由于该类数据的样本量极大，分析和处理的难度以及效果较差，甚至无法完成原始高维数据的加载；并且，即便在实现加载的情况下，也会导致计算机资源的超量占用，对算法的运算效率造成较大影响[2，3]。

当前，诸多学者针对高维数据的增量式聚类均展开相关研究，例如赵萌萌等人基于共享近邻紧密度，研究高维数据的增量式聚类算法[4]，斯亚民基于嵌入式模糊集数据库，研究高维数据的增量式聚类算法[5]。上述算法，可用于完成正常数据的聚类处理，但是当数据信息流中存在异常数据时，上述方法的敏感性较强，则处理效果较差。

本文结合高维数据的特点，依据spark技术对高维数据的增量式聚类算法进行改进，提出基于改进spark技术的高维数据增量式聚类算法，实现高维数据的有效聚类处理，且避免敏感性的发生，提升数据处理效率。spark技术是一种用于处理大数据的计算引擎，也可理解为一种通用的并行架构，可实现交互式计算，可高效完成大数据的处理，并且通用性能较好，可适用于多种程序，实用性能较高，支持复杂算法的运算。增量式聚类是一种以提升数据聚类效果以及效率为目的，在上一次聚类的基础上，提升此次聚类效率的一种聚类算法。该算法也是用于实现高维数据处理的一种主要方法。

2 基于改进spark技术的高维数据增量式聚类算法

2.1 高维数据结构重组

高维数据中，含有大量模糊数据，对高维数据的处理造成一定影响。因此，为实现高维数据增量式聚类，需重组高维数据结构，获取数据中的模糊数据。本文采用基于混沌分区方法完成。依据获取的模糊数据分析该数据的时间序列混沌序列，以此分析两种结构[6]，分别为重构结构及数据结构，前者属于模糊数据。

{x1，x2，…，xN}表示观测时间序列，属于高维数据流，且为待挖掘状态；宽带时间序列用x(n)表示，处于平稳状态；对模糊数据结构映射，且在特征空间中完成，其维数用m表示，基于此可得重组结构公式，且属于高维数据

X(n)={x(n)，x(n+τ)，…，x(n+(m-1)τ)}

(1)

式中：n=1，2，…，N；τ表示时间延迟。

为获取模糊信息的分布轨迹[7]，需在完成特征融合的基础上，分析相轨迹演化情况，且处于高维空间内完成，则公式为

X=[s1，s2，…，sK]

(2)

式中：K表示嵌入维数，K=N-(m-1)τ，属于特征空间，且在搜索过程中；m表示层数，属于数据的本体特征；特征矢量集用si表示，属于相空间中，且si=(xi，xi+1，…，xi+(m-1)τ)T。

2.2 高维数据降维

由于获取的模糊数据的分布轨迹呈不均匀分布状态，并且数据的维数较高，因此，本文采用基于信息熵的高维稀疏降维算法，先该分布空间的高维数据进行特征筛选后，减少特征的数量，然后完成数据降维[8]。

阈值用δ表示，属于信息熵，通过减少数据特征数量，将无效的原始数据特征去除，其降维过程如下所述：

输入：输入X，X包含的样本数量为m、特征数量为n；贡献率为f。

输出：降维结果Yk×m。

1)对数据的所有特征进行求解，将求解结果与δ进行对比，进行特征选取，对X进行相关操作，操作内容为：求解特征ai的信息熵H(ai)；向集合A中引入ai。

2)为获取矩阵Vn×m，中心化处理样本矩阵

V=A-repmat(mean(A，2)，1，m)

(3)

3)为形成方差矩阵Cov，需求解其协方差，属于差异性特征之间

Cov=(VVT)/(size(X，2)-1)

(4)

4)求解Cov的特征值和特征向量。

5)选择并确定变换基：

为构成特征向量矩阵Wn×k，选取最大的特征值的特征向量完成[9]，两者的数量均为k。

6)降维结果求解，其公式为

Y=WTV

(5)

7)输出结果

算法中f决定k值，f的计算公式为

(6)

式中：λi表示特征根。

2.3 并行化增量式高维数据聚类优化

2.3.1 关联数据检测

检测输出Yk×m，获取数据之间关联性。设γBLCMV表示Yk×m的监测统计特征值，其计算公式为

(7)

式中，检索的模糊域用at(θ)表示；R表示优化目标函数；φ表示分块匹配集，且φ=[φ1，φ2，…，φg]，其式(8)描述

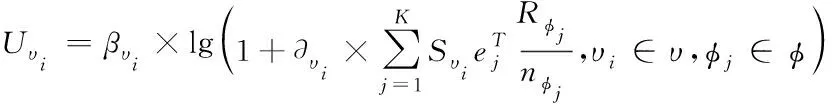
(8)

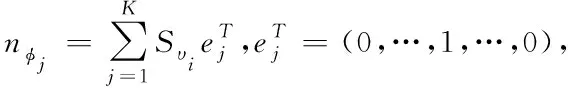
(9)

式中：ASM表示加权幅值，且为输出；ρSM表示自适应调节参数；DSM表示约束条件，且为不等式；H表示特征分布系数。

设定时间窗口为Tφ，其属于模糊类中心，计算公式为

Tφ=set(Tf/Nφ)

(10)

式中：Tf>φjTφ；Nφ表示φ的数量。

Yk×m的全局性最优返回结果为

pi(l+1)=min(pmax，Ωi(l+1))

(11)

将式(11)结果输入至缓冲器中，获取链路增益值hi，且hi≠hmin(l)、Ωi(l)>0，基于此完成Yk×m中关联数据检测。

2.3.2 改进spark融合聚类

为实现高维数据的增量式聚类，采用spark融合聚类方法[10]对提取的特征向量进行并行聚类优化，且在高维相空间中完成，获取高维数据功率谱密度，且属于传输信道，其计算公式为

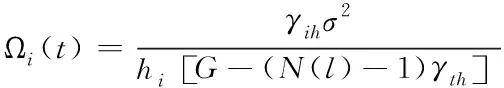
(12)

设pi(l+1)=0，描述高维数据的输出斜度和峰度，两者的计算公式依次为

Sx=E[x3(t)]

(13)

Kx=E[x4(t)]-3E2[x2(t)]

(14)

并行化聚类的误差计算公式为

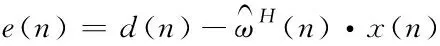
(15)

式中：μ表示特征分量；d(n)表示期望距离，ω表示间距。

为获取高维数据的均衡调度尺度特征，需提取高维数据的平均集对特征量，其属于集对簇中[11]，并且位于信道的近场源中完成。

(16)

式中：E(i，j)表示均衡调度尺度特征；依据各个时帧A中的簇向量集ai，获取高维数据并行化聚类的R，其计算公式为

R=ω1Ci+ω2Di+ω3Mi+ω4Ni

(17)

式中：ω表示间距，且在扰动情况下，并属于聚类类间；C、D分别表示频率和尺度，两者均属于数据聚类过程中，且前者对应子带中心，后者对应时间；M表示约束参量，且呈线性。则高维数据的spark融合[12]的高维数据增量式聚类集计算公式为

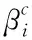
Qkc(-1)i+1det(Q′i1)))

(18)

K(xi，xj)=〈xi，xj〉

(19)

结合自适应学习算法完成高维数据聚类中的自动寻找，完成高维数据并行化聚类。

3 仿真测试与分析

为测试本文算法的聚类效果和性能，本文选择两种不同维度的数据集作为测试对象，数据集1包含样本总数量为1799，其维度为256，类别数量为12；数据集2包含样本总数量为400，其维度为1024，类别数量为400，测试时，测试过程中通过Visual C++完成算法编译，并采用MATLAB仿真软件完成测试。

为测试本文方法的高维数据的结构重构效果，需确定其最佳嵌入维数，测试在不同维数下，数据集的混沌重组结果，数据集1的重构效果如图1。

图1 混沌重构测试结果

根据图1测试结果可得：嵌入维数为5时，混沌重构分区后的数据分布存在尖峰位置，虽然整体呈现上下分布，但是中心线的上下两部分存在一定不对称现象；嵌入维数为7时，混沌重构分区后的数据分布平滑、圆满，不存在尖峰现象，并且中心线上下部分呈现较好的对称分布；嵌入维数为9时，混沌重构分区后的数据分布则出现较为明显波动，则波动状态不规则，导致纵向中心线和横向中心线呈现差异变化。该结果表明，当嵌入维数为7时，可获取最佳的数据混沌重构效果。

为测试本方法对高维数据的降维效果，采用本文方法对两类数据集进行降维处理，测试在不同贡献率取值下，两类数据集降维前后的对比结果，见表1。

表1 两类数据集的降维测试结果

分析表1测试结果可知：本文算法具备良好的数据降维效果，针对维数相对较低和相对较高的两种数据集的降维性能相差较小，不存在维数越高则降维效果较差现象。当贡献率达到1.0时，两种数据集的维度分别下降120和118个维度，有效实现数据集的维度下降，以此降低存储空间的占用率。

为测试本文算法的聚类效果，采用归一化互信息和兰德指数作为评价指标，指标的计算公式分别为：

(20)

(21)

式中：数据集的样本总数量用N表示；第i类的样本数量用Ai表示，且属于本文方法聚类后；数据集中的真实数量用Bi表示，且属于第j类样本；ζ表示未知类别；以实际的样本类别信息为参照，聚类后与其类别相同的样本数量用a表示、不相同的数量用b表示。两个评价指标的取值范围为[0，1]，本文方法的聚类效果随着该取值的增加而越佳、该取值的降低而变差。

所提方法下两类数据集的聚类的效果，结果见图2、图3。

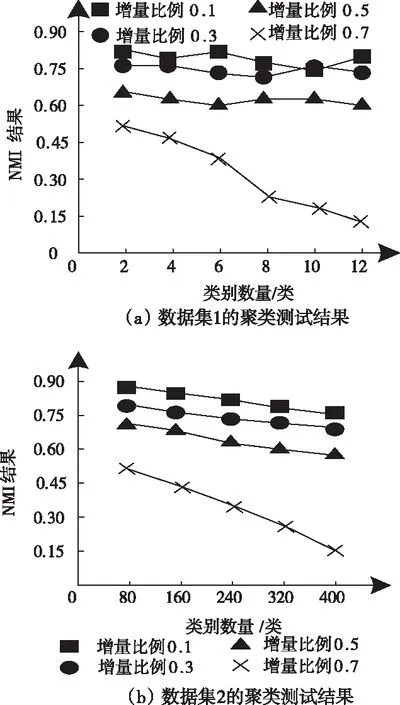
图2 归一化互信息测试结果

依据图2测试结果可知：当样本类别数量较少时，在不同的增益比例下，NMI呈现差异性波动变化，但是当期比例达到0.7时，NMI的结果较低，随着样本类别数量的增加，呈现显著的下降趋势；当样本中类别数量较多时，随着样本数量的增加，不同增益比例下的NMI值均呈现下降趋势，但是，比例为0.1、0.3、0.5时，NMI的结果均在0.58以上，当比例为0.7时，NMI的结果均低于0.55，并且样本数量为12类时NMI的结果仅为0.15。

图3 兰德指数测试结果

依据图3测试结果可知：增益比例为0.1、0.3、0.5时，数据集1和数据集2的RI结果均在0.60以上，且波动范围较小，当增益比例为0.7时，数据集1的RI值，随着样本类别数量的增加，在0.3～0.45的范围内波动；数据集2的RI值随着样本类别数量的增加，则呈现缓慢下降趋势。

综合图2和图3结果得出：增益比例对于NMI的结果存在直接影响，因此，算法在运算过程中，比例值应低于0.5，同时，在合理的比例取值下，样本数量的增加，对于NMI的结果影响较小，可忽略不计。因此，在合理的增益比例下，本文算法的聚类效果良好，可完成高维数据的有效、可靠聚类。

4 结论

由于高维数据的利用率以及处理效果不理想，因此，本文以高维数据增量式聚类为目的，研究基于改进spark技术的高维数据增量式聚类算法。通过高维数据结构重构、降维处理，并通过spark技术完成数据的并行聚类优化，实现高维数据的高效处理，获取有效数据，实现高维数据的增量式聚类。通过仿真测试得出：本文算法在最佳的嵌入维数下，可完成最佳的数据结构重构结果，并且能够降低高维数据的维度，聚类效果良好。

在日后的研究中，将以进一步提升算法的性能为主，对高维数据中的近似特征展开研究，分析是否可通过近似特征的结合，优化算法的聚类性能。