物流分销网络双层规划算法的设计与仿真

金 婕，金 睿

(1. 湖北工业大学工程技术学院，湖北 武汉 430068；2. 武汉大学电子信息学院，湖北 武汉 430064)

1 引言

当前，我国大多数企业都存在物流成本过高的现象，主要原因是物流系统运作效率低，而企业物流结构的好坏主要与企业物流网络结构相关。优秀的物流结构能够将物流系统内各个要素有效集成，并能够缓解各个接口无缝化衔接，降低物流成本。在此背景下，许多学者对企业物流网络中的物流分销网络体系机理与规划理论进行了大量研究。其中，文献[1]中，王亚东等人研究了动态物流网络多目标优化模型及求解算法，该算法将自适应多目标差分进化算法应用到目标设置中，并采用差分进化策略对计算结果不断迭代收敛，判断个体优势，完成分销网络规划；文献[2]中，蔡鉴明等人研究了基于碳税政策的整车物流网络优化模型及算法，该算法建立鲁棒优化模型，采用遗传退火算法求解模型，实现网络规划；文献[3]中，王诺等人研究了面向远海岛礁群的双向物流网络规划方法，该方法将成本最低作为设计原则，提出双层并行搜索遗传算法，完成双层网络规划。上述方法虽然能够实现网络双层规划，但是在规划过程中花费的时间较长，规划后花费的成本也不是很低，不能满足物流分销网络的设计需求。

均衡原理近几年发展较快，在网络规划中有了较为广泛的应用，并获得了不错的应用效果。基于此，设计一个基于均衡原理的物流分销网络双层规划算法，期望解决当前物流分销网络存在的问题。

2 均衡模型构建

物流分销网络规划是一项较为复杂的系统工程，其涉及的目标较多，为此从社会经济、物流服务能力等多方面出发，建立规划指标体系[4]，如表1所示。

表1 规划指标体系

结合规划指标的相关数据，建立初始规划矩阵，为各个指标设置均衡条件

(1)

上述公式中，n代表指标，m代表城市数量。

由于规划的指标中一般都包含高优指标和低优指标，高优主要代表该指标值越大越好，低优指该类指标值越小越好[5]。为此分别对其处理，将高优指标处理为

yij=xij

(2)

将低优指标处理为

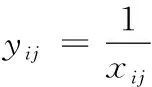
(3)

上述公式中，xij、yij分别代表高指标x与低指标y的处理参数。

在此基础上，基于均衡原理，建立均衡数学模型，将其数学形式描述如下：

(4)

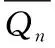
在交通的控制上，控制过程如图1所示。

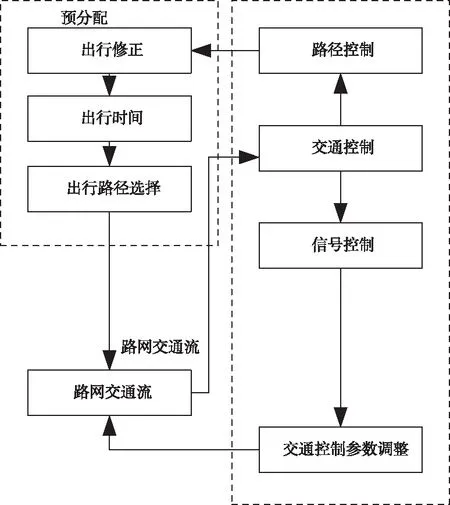
图1 物流交通控制过程

基于上述过程对物流分销网络双层规划中涉及的各个指标设置均衡条件，并对物流交通条件进行考虑，使后期规划都满足均衡条件[6]。

3 物流分销网络双层规划模型构建

3.1 模型假设条件建立

在不影响备件物流分销网络主要特征的前提下，提出以下假设条件：

第一，顾客的需求是随机的，并服从泊松分布，将概率分布函数表示为

(5)

式(5)中，e代表没有按照规定时间配送的惩罚费用，λ代表顾客需求均值。

第二，备件的品种相同，不存在层次性特征；

第三，分销之间不存在紧急转运情况，为此只需要对初始的分销中心点计算即可[7]，采用下述公式对分销中心订货点计算

(6)

上述公式中，α代表服务水平要求参数，该参数为不发生缺货的概率参数。

第四，假设每条运输线路上只有一辆车，为此在运输过程中需要订货批量，以满足运输需求，由于销售是随机需求，为此采用期望值对随机需求处理[8]，将其表示为

(7)

式(7)中，μj代表在分销中心中用户对j的需求量，Kj代表分销j产品的订货费用，CV代表每次分销中车辆的派遣费用，Cp代表单位时间内物品的存储费用。

通过上述过程建立起假设条件，为分销网络双层规划提供基础。

3.2 上层及下层规划

在物流配送过程中，上层的决策部门能够通过管理改变物流中心的位置，从而对下层客户对物流中心选择造成影响，然后不能控制用户自身的选择。用户可以根据自身需求选择物流中心服务，这种关系可以用双层规划模型描述[9，10]。在上下层选择过程中需要在均衡数学模型下进行，以保证选择与被选择的项目是合理的[11]。

预先对上层规划，将物流网络供应节点集定义为A={a∣a=1，2，…，n}，将物流相关客户的集合定义为B={b∣b=1，2，…，n}，将已经存在的物流网络节点集记作C={c∣c=1，2，…，n}，将新增节点的候选集记作D={d∣d=s+1，s+2，…，s+n}，将物流网络中所有的备选节点集记作E=C∪D。

在上述物流需求网络结构定义完成的基础上，建立区间参数约束下的上层规划模型，如下所示

(8)

式(8)中，Yη代表决策变量，ai、bj代表网络整个区间内物流产生的需求参数，Fmin代表区间节点最小的需求量。

在此基础上，对下层规划，下层主要对用户需求量在不同节点间的分配模式，在下层规划中将用户话费的费用最低作为目标[12]，模型如下所示

(9)

3.3 上层及下层规划求解

在通常情况下，通过上层决策者对下层进行控制是不切实际的，为此需要进一步求解。使下层决策者在可行空间内搜寻最优解，在减少求解时间的同时减少相互反应次数[13]。

在求解过程中，上层及下层中涉及的变量与参数都为非负约束，在区间内运算满足x∈[xmin，xmax]，为此将上下层目标函数的变化区间确定为：

(10)

式(10)中，W代表上层约束，M代表下层约束。

在上下双层约束求解过程中是一种自下而上的求解过程，为此对下层问题定义，将下层M中的任意值，定义风险系数，将其表示为

(11)

式(11)中，η代表风险因子。

为避免上层求解出现偏差，提出最大决策偏差约束条件，将其表示为

d(W)=Wmax(x)-Wmin(x)×dmax

(12)

式(12)中，d代表预先给定的误差控制范围参数。

在求解完成后，将均衡条件考虑在内，对网络规划，其流程如图2所示。

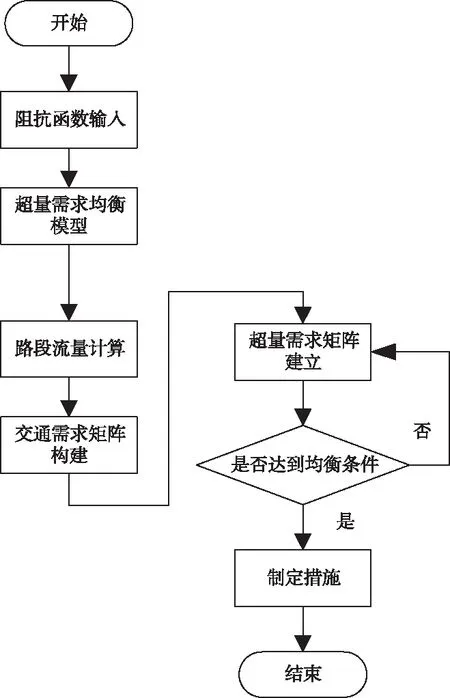
图2 基于均衡原理的规划流程

在上下双层规划过程中，各个变量是会实时发生变化的，最终求解结果也会随之发生变化，为此进一步处理，将双层规划中涉及的变量编码处理，采用区间编号的模式定义编码集[14，15]，表示如下

P=[x1，x2，x3，…，xn]*ye

(13)

式(13)中，ye代表初始种群集，x1、x2、x3、xn分别代表每个编码参数对应的区间值参数。

不断重复上述计算，直到求解出最优解为止，以此完成物流分销网络上层规划。

4 实验

为验证提出的基于均衡原理的物流分销网络双层规划算法的有效性，采用某公司相关数据进行算例分析。并将动态物流网络多目标优化模型、基于碳税政策的模型、面向远海岛礁群的双向物流网络规划方法与所提出的方法对比。

4.1 实验对象

该实验公司物流分销网络主要包含2个制造商工厂、3个仓库、2个备选物流企业和10户需求点组成。主要需求内容如下所示：

表2 实验公司相关数据

实验中，配送中心以及配送路径图如图3所示。

图3 配送中心及配送路径图

分别采用所提出的规划算法与其它三种方法对该公司物流分销网络规划，详细对比结果如下。

4.2 实验结果

1)配送成本

在配送成本对比上，主要分析中央仓库与物流需求点的配送成本，在配送上将第三方物流企业作为中转点，其中，5个中央仓库到第三方物流企业的配送成本如图4所示。

图4 中央仓库到第三方物流企业配送成本

基于上图能够看出，动态物流网络多目标优化模型及求解算法在配送上花费的成本是最高的，所研究的分销网络双层规划算法花费成本最少，其余两种方法虽然没有动态物流网络多目标优化模型花费的成本高，但是仍然多于所研究的规划方法很多。

第三方物流企业到10个物流需求点花费的物流配送成本如表3所示。

表3 第三方物流企业到物流需求点配送成本

通过分析上表可知，在10个物流需求点物品的配送上，所提出的网络双层规划算法花费的配送成本仍然是最少的。其它三种方法配送成本均高于所提出方法，其中基于碳税政策的规划方法配送成本最高达到2500，说明这三种方法规划效果较差，不能节省物流配送成本。

2)平均配送时间

5个中央仓库到第三方物流企业的配送时间如图5所示。

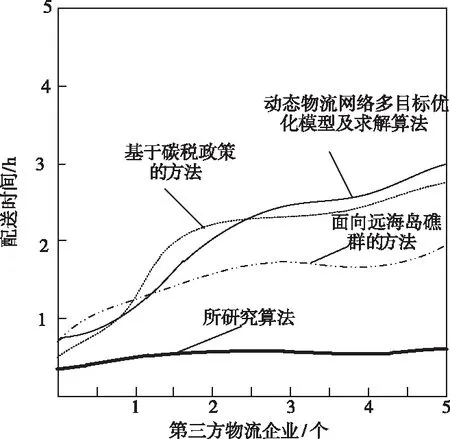
图5 中央仓库到第三方物流企业的配送时间

基于上图可知，在配送时间上，其它三种方法的配送时间均高于所提出的规划算法，证明所研究的算法有效提高了物流配送效率，规划效果较好。

第三方物流企业到10个物流需求点花费的配送时间如表4所示。

表4 第三方物流企业到物流需求点花费的时间

通过分析上表可以看出，所研究的物流分销网络双层规划算法花费的配送时间是最少的，应用效果好于其它三种方法。所研究方法获得较好效果的原因是预先构建了均衡模型，使后期规划双方都能够保持均衡，将花费的时间与成本都控制在合理范围内。并在规划中，对上层与下层网络分层规划，并进行求解，从而提高了物流分销网络双层规划效果。

5 结束语

综上所述，完成基于均衡原理的物流分销双层规划方法，实验结果表明所提出的规划算法不仅减少了规划成本，还提高了规划效率。因为双层规划模型能够充分考虑时间约束与顾客选择行为，并通过均衡原理有利于对利益协调，总成本控制，在指导现实的物流分销网络中有重要的意义。

但是，实际配送中会受到多种因素的影响，在影响因素分析上还需要花费一定的时间进行研究，以进一步提高分销网络双层规划效果。