基于三维点云的精密偶件筛选及虚拟装配方法
杨文超,惠宏超,张晓玲
(北京航天控制仪器研究所,北京 100039)
1 引言
半球动压陀螺电机是新一代高精度机械式惯性仪表——惯性仪表的核心部件,惯性仪表实现测量功能所需的角动量就是由其高速旋转产生,即“陀螺效应”。惯性仪表的精度很大程度上取决于陀螺电机的角动量大小,同时陀螺电机的寿命也直接决定了惯性仪表的寿命,因此陀螺电机的性能指标直接影响惯性仪表的精度和可靠性[1]。精密偶件作为动压陀螺电机的核心零件,主要由半球和球碗零件组成,目前在生产过程中,只能依靠高精度三坐标测试机、圆度仪、粗糙度仪等设备对半球和球碗分别进行检测,检测项目多,检测效率低,测量周期较长,且只是对零件局部某区域的几何特征进行检测,具有一定的片面性,容易忽略存在较大误差的区域,不能覆盖零件整体几何特征[2]。
为了提高检测精度、保证检测效率、获取完整的几何特征检测结果,采用三维点云处理技术完成零件的筛选及虚拟装配。高精度三维点云数据通过泰勒LuphoScan多波长干涉扫描测量系统获取,系统使用了复杂的参考传感器以及特殊的基准框架概念,能够确保最高精度的测量结果,精度可达±0.05μm,重复精度可达±0.02μm,且系统测量时间较快,约为1min,采集的点云个数约为70000个。在几何尺寸方面,采用最小二乘点云拟合算法计算出半球、球碗零件的球径值和球心坐标,根据球径精度要求筛选出合格的半球、球碗零件;在微观形貌方面,对点云数据进行重构,生成误差实体模型,分析误差实体模型的表面形貌,确定零件表面形貌的变化范围以及极大误差点,剔除不符合要求的零件。最后,确定半球和球碗零件的粗配准则,筛选出能够配对的偶件组合,根据点云特征参数的位置关系要求,确定半球和球碗的静态对准原则,完成虚拟装配,进行模拟实际工作状态的动态测量,实现组件工作间隙的3D显示[3]。
2 基于最小二乘法的半球、球碗零件特征参数提取
半球、球碗初始点云数据包括七万左右个数据点,且点云表面的曲率变化较为简单,点云特征规则,如图1所示。

图1 半球、球碗零件初始点云数据
根据球径误差分析的需要,确定采用最小二乘法对零件的球心以及球径进行拟合求解,算法适用于表面变化平稳的点云数据,注重保留点云表面的光顺特性,最小二乘法进行点云拟合的基本过程如下[4]:
对于半球、球碗零件来说它是一个单一的型面,整个零件是由一个型面组成,根据上述的最小二乘法点云拟合的基本过程,需要通过采集得到的n个零件三维点云数Pi(xi,yi,zi)的坐标值拟合出球心坐标和球径长度。若零件的球心坐标为(A,B,C),半径为r,则半球球面的定义函数为
(X-A)2+(Y-B)2+(Z-C)2=r2
(1)
令a=-2A,b=-2B,c=-2C,d=A2+B2+C2-r2,那么半球球面方程可以写成
X2+Y2+Z2+aX+bY+cZ+d=0
(2)
由上式可得样本点Pi(xi,yi,zi)的残差为

(3)
残差的平方和为
+axi+byi+czi+d]2
(4)
其中,残差的平方和L(a,b,c,d)一定大于零,因此该函数存在大于或等于零的极小值。分别对函数L(a,b,c,d)中的参数a,b,c,d求偏导数,并令其偏导数的函数值为零即可求得函数的极值点。

(5)
将上式消参后可得

(6)
令式中
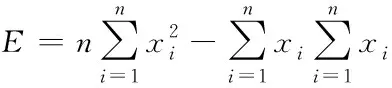
(7)

(8)

(9)
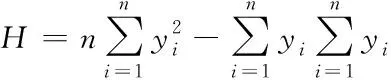
(10)

(11)
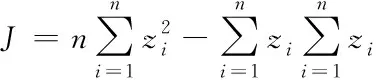
(12)
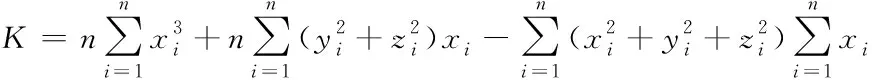
(13)
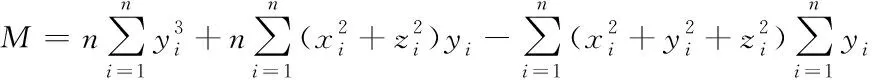
(14)

(15)
之后将上述结果代入式中,可将该式化简为

(16)
求解方程组即可得到参数a,b,c的值,将a,b,c代入到第四式中可求得参数d。最后可以得到半球点云球心坐标及球径为

(17)
表1为零件几何尺寸的误差结果统计,将上述采用最小二乘法拟合得到的球径结果与理论球径值进行比较,若拟合得到的球径值在半球球径加工要求的范围内,则该零件满足要求,可以进行后续表面形貌的误差分析;反之,则零件不满足加工要求,需要对该零件进行剔除。
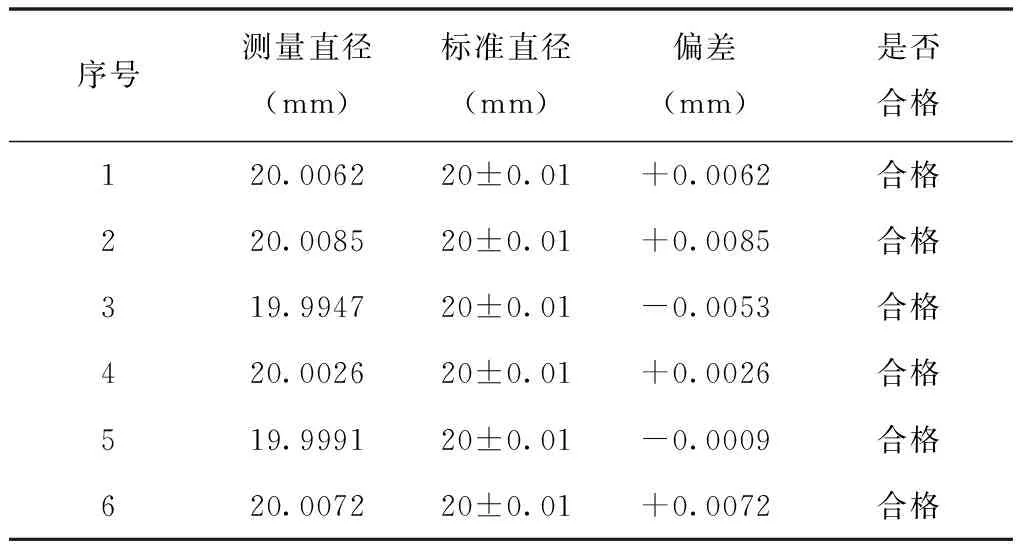
表1 零件几何尺寸误差统计
3 半球、球碗零件三维点云数据微观形貌分析
采用三维点云技术来分析零件的表面微观形貌,可以得到整个半球、球碗球体与标准球体的偏差值,从而在整体上完成零件表面微观形貌的分析。采用基于Lawson算法的Delaunay三角剖分法对半球、球碗的三维点云数据进行重构,该算法能够使零件点云保持原始数据,并且能够保留零件点云表面的细微特征,算法的拟合结果更趋近于零件的真实形貌[5],点云重构后的三角面片数约为150000个,重构后的模型表面积约为250mm2,单个三角面片的面积约为0.0017mm2,图2为零件点云数据采用Delaunay三角剖分的重构结果示意图;图3为Delaunay三角剖分结果的局部放大图。

图2 Delaunay三角剖分重构结果

图3 Delaunay三角剖分局部放大
根据最小二乘法拟合得到的零件球心坐标和球径值,构造与零件球体特征对应的标准球体模型,将Delaunay三角剖分的点云重构结果与标准球体模型进行比较,从而对零件的表面形貌进行误差分析,基于半球和球碗点云表面形貌分析示意图如图4所示,图中R0为最小二乘法拟合得到的球径值,R1、R2为零件球径的变化区间,红线部分为零件表面的真实形貌。

图4 点云表面形貌分析示意图
零件表面形貌误差分析主要是分析重构模型的整体三维偏差,得到一个全面、直观、形象的轴承偶件整体表面形貌的信息,并以三维彩色色斑图表现出点云表面上各个点的偏差情况,且能够对表面上各个点进行注释,使得该点的形貌信息被直接检测到,通过该方法确定零件点云区域内的球度误差以及极大值误差,图5所示为零件表面形貌偏差色斑图。

图5 零件表面形貌偏差色斑图
表2为半球和球碗表面形貌误差统计结果,若偏差色斑图中的半径变化均位于-0.3μm≤ΔR≤0.3μm" 范围内,则证明半球和球碗的表面形貌满足球度误差要求,该零件合格,若零件表面形貌中存在不满足半径要求的点云区域,则证明该区域不符合零件球度要求,通过上述方法可以准确地筛选出满足微观特征要求的合格零件,记录合格零件的球心坐标以及球径值,将其作为后续零件进行粗配的前提条件,能够省去径向间隙调整工序,实现数字化预装配。
4 组件间隙测量
组件间隙是否合适直接决定了气浮轴承工作的稳定性和工作寿命,实现组件间隙的测量首先要完成半球和球碗零件的粗配,以上述最小二乘法拟合得到的合格半球和球碗零件的球径值为依据,判断球碗的球径值是否大于半球的球径值,且两者的球径差为4~5μm,若满足上述条件,则可以进行后续的静态匹配对准;若不满足,则需要根据半球的球径值选择下一个球碗继续进行粗配,直至配对出符合要求的半球和球碗。
根据上述组件粗配准则可以筛选出符合装配要求的半球和球碗的三维点云数据,但是由于半球和球碗的三维点云数据并非在同一坐标系下测得,因此需要将两者的点云数据统一到同一坐标系下,完成静态匹配对准,静态匹配对准的约束条件如下:①半球拟合得到的球心坐标与球碗拟合得到的球心坐标重合;②半球点云的旋转轴与球碗点云的旋转轴重合且正方向一致。如图6所示为半球和球碗点云坐标系的统一过程。

图6 半球和球碗点云坐标系统一过程
半球和球碗点云静态配准之后,即可进行组件工作间隙的测量,测量过程需要模拟组件的实际工作情况,以X轴正方向为0度,采用球碗沿轴线顺时针旋转6次的方法模拟组件的转动,在360度范围内依次沿轴线旋转角度为0度、60度、120度、180度、240度和300度,在每一个位置建立基于颜色索引的色斑图将双边间隙偏差可视化[6]。图7所示为组件在不同位置工作间隙的偏差色斑图。

图7 不同位置处组件工作间隙的偏差色斑图
5 实验结果及分析
通过瑞士TESA电感测微仪(不确定度0.1μm,量程0.5mm),对通过点云配对的组件进行轴承间隙检测。若符合轴承间隙(单侧轴承间隙)1~2μm,即为轴承偶件一次装配成功。一次装配成功率=符合要求的轴承数量/点云配对的轴承数量×100%。
统计30个左半球、30个右半球,60个球碗,通过点云进行配对,得到30只马达轴承间隙数据,统计点云配对的轴承零件轴承间隙检测值与电感测微仪实测值[7]。
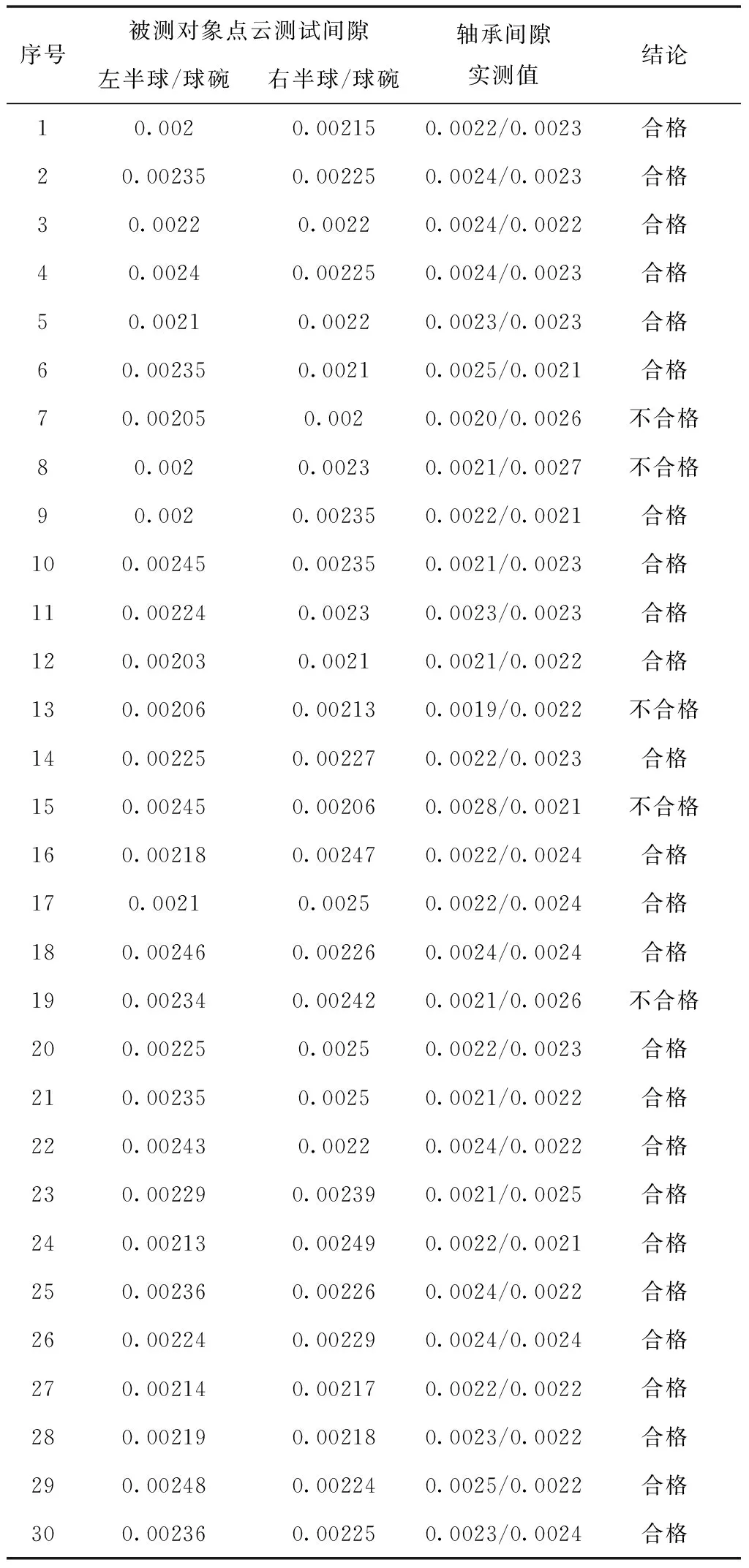
表3 马达轴承零件轴承间隙检测结果
由表3可知30只马达轴承间隙数据中通过电感测微仪验证存在5组不合格结果,则马达装配一次成功率为83.3%。
6 结论
文中首先将采集得到的半球、球碗零件的三维点云数据进行基于最小二乘法的特征参数提取,计算得到球径值及球心坐标,将球径值与半球、球碗零件的标准值进行比较,完成几何尺寸上的零件筛选;然后对零件的表面形貌进行分析,确定零件整体的表面形貌误差,从而在微观形貌上对零件进行进一步筛选;最后将筛选得到的合格半球、球碗零件进行粗配,再通过特征参数对齐法完成零件的虚拟装配,从而得到组件的动态工作间隙变化。实验结果表明,文中提出的基于三维点云数据的零件筛选及虚拟装配方法,为半球、球碗零件装配提供了较为可靠的技术支持,提高了零件的装配效率及合格率。

