CEEMDAN与多特征融合的脑电信号识别研究

张聪聪，常湛源，2，李传江

(1. 上海师范大学信息与机电工程学院，上海 200234；2. 上海智能教育大数据工程技术研究中心，上海 200234)

1 引言

脑机接口(brain computer interface，BCI)技术不依赖于神经和肌肉，仅通过大脑可以为运动障碍者提供一个重要的新的向外部世界发送信息和控制命令的选择[1-3]，分为侵入式和非侵入式两种，侵入式脑机接口通常直接植入到大脑的灰质，因而所获取的神经信号的质量比较高但其容易引发免疫反应，非侵入式脑机接口因其装置方便佩戴于人体而成为研究重点[4]，在BCI系统的脑电活动中，运动想象不依赖于外部事件，以其反应主动运动意图的优势成为研究的热点。

BCI系统的关键技术是对想象运动脑思维活动所产生的脑电信号进行综合分析，提取不同类别脑电信号的特征，对特征进行分类识别运动意图。用于表示脑电信号运动意图的常见特征是时域、频域、空域特征，其中时域特征有幅值和幅值能量等，频域特征有功率谱密度(Power Spectral Density，PSD)、自回归模型系数等，空域特征有无监督的主成分分析(Principal Component Analysis，PCA)、独立成分分析(Independent Component Analysis，ICA)和有监督的共空间模式(Common Spatial Patterns，CSP)等方法获取[5-6]。根据脑电信号的非线性、非平稳的特性，时频域分析的方法应用越来越广泛，例如希尔伯特-黄变换(Hilbert-Huang Transform，HHT)[7]、小波变换(Wavelet Transform，WT)[8]和小波包变换(Wavelet Packet Transform，WPT)[9]。

近年来，多特征融合的方法取得较多成果，与单一特征相比，多个特征结合的方法取得了更高的分类精度[10-11]。例如，在运动想象分类领域，文献[12]将HHT提取的边际谱和瞬时能量谱结合近似熵进行多特征研究，所有被试者平均识别率高于80%；在情感分类领域，文献[13]结合6种时域情感特征进行分类研究，并将小波特征和信息熵组成复合特征，都达到较高识别率；在脑卒分类领域，文献[14]将层次理论、小波包能量和模糊熵相结合，得到的分类精度远高于单一基准特征。在HHT时-频分析中，首先通过EMD将原始信号分解为IMF分量，EMD分解的IMF摆脱了傅里叶变换的局限性，与小波变换和小波包变换相比，EMD不需要基函数，克服了小波基函数无自适应性的问题，对于一段未知信号可直接分解。但EMD的缺点是模态混叠，EEMD更好地解决了模态混叠问题[15]，但EEMD分解在多次试验集成平均后，重构的各个模式分量中仍然含有一定幅值的残留噪声。因此，本文引入CEEMDAN方法来克服EMD分解和EEMD分解效率低和模态混叠的问题，CEEMDAN方法的分解过程具有较好的完备性，并可以提高信号重构的准确性[16]。熵度量了一个系统或一段信息的不确定性，将样本熵(Sample Entropy，SampEn)、近似熵(Approximate Entropy，ApEn)、模糊熵等非线性动力学特征引入心电、肌电、脑电等信号的数据处理具有很大优越性[17]。模糊熵(Fuzzy Entropy，FuzzyEn)通过模糊函数得到的更多细节也使得其比样本熵和近似熵更精确地定义了熵，此外，模糊熵的相对一致性更强，对数据长度的依赖性更小[18]。因此，本文选用模糊熵作为运动想象信号的非线性动力学特征。

群体智能优化算法因具有结构简单、易于实现等特点，被广泛应用于复杂问题的求解中。灰狼算法(Grey Wolf Optimizer，GWO)自提出以来，就因具有良好的性能而引起了众多学者的广泛关注。在函数优化方面，已经证明GWO的收敛速度和求解精度优于粒子群优化算法(Particle Swarm Optimization，PSO)、引力搜索算法(Gravitational Search Algorithm，GSA)、差分进化算法(Differential Evolution，DE)、进化规划(evolutionary programming，EP)和进化策略(Evolution Strategy，ES)[19]。在各种分类器中，支持向量机(Support Vector Machines，SVM)因其对非平稳数据的通用性和鲁棒性而被广泛应用于脑机接口中[20]。

为提高运动想象分类正确率，为脑电信号模式识别研究提供一种新的识别方法和研究思路，本文引入CEEMDAN方法应用于运动想象脑电信号特征提取，对信号进行加时间窗滑动改进分解，获取更多的处理数据，增加脑电信号的利用率，并结合时-频-空域-非线性动力学的多特征组合的方法进行处理分析，分类器选用GWO-SVM。结果表明，多特征融合互补，融合识别率高于单一特征，加时间窗的CEEMDAN分解方法可以提高分类正确率。

2 实验数据

本研究所采用的数据集为BCI Competition II的Data set III竞赛数据，由格拉茨理工大学(TU Graz)生物医学工程研究所医学信息学系提供(http：∥bbci.de/competition/ii/download/)。受试者为一位25岁女性，受试者以放松状态坐在椅子上，试验任务是通过显示器随机的左右提示来想象左手和右手运动获得反馈数据。实验共有7组，每组40次，所有实验都在同一天进行，中间休息几分钟。数据给出了280个9s长的试验。其中t=2时，声刺激提示试验开始，显示器“+”显示1s；然后t=3时，箭头(左或右)显示为左右运动提示，同时要求受试者开始想象运动，即运动想象时间为3s～9s。图1为单次试验方案设计。单次试验中考虑到受试者从看到提示到开始想象运动之间会有反应延时，同时持续运动想象时间长会导致疲劳，容易引入较多噪声，因此，本文中截取中间4s～8s的信号作为研究对象。

试验采用Ag/AgCl电极，通过C3、Cz、C4三通道获得反馈数据，其中C3和C4电极位于大脑的初级感觉皮层运动功能区，反应受试者在想象左手和右手运动时的状态变化，因此，本文实验分析选取C3和C4通道。试验电极位置分布如图2所示。信号的采样频率为128 Hz，原始信号经过0.5～30 Hz的带通滤波器。图2为试验电极位置。在本文中，为增加试验数据处理次数得到更加合理的结果，采用k折交叉验证的思想，将280次试验分为4组，每组70次，选取其中的3组作为训练集剩下一组为测试集，选取4次，第五组试验数据为原始140次训练和140次测试数据，最终试验结果为5组试验结果的平均值。

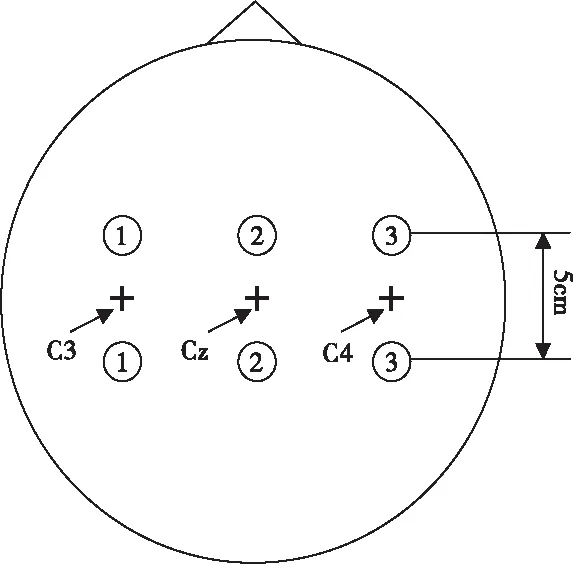
图2 试验电极位置

3 方法

3.1 CEEMDAN方法

EMD方法依据数据自身的时间尺度特征来进行信号分解，无须预先设定基函数。EEMD方法把高斯白噪声引入要分析的信号中。由于零均值噪声的特性，噪音经过多次的平均计算后会相互抵消，这样集成均值的计算结果就可以直接视作最终结果，显著提高EMD算法的稳定性。CEEMDAN在EEMD的基础上，在分解的每一个阶段自适应加入均值为0、方差为1的高斯白噪声序列，计算唯一的余量信号来得到各个IMF分量。具体实现过程如下：

1) 将原始信号f(t)与白噪声ni(t)相结合，ε为信噪比控制系数，构造噪声信号fi(t)，得到N个噪声信号fi(t)=f(t)+εni(t)，i=1，2，…，N；利用EMD分解各fi(t)，得到IMF1的ci1(t)及其残余项ri(t)，计算ci1(t)的平均值，得到CEEMDAN的第一个IMF分量c1(t)：

(1)

2) 从f(t)中减去c1(t)得到剩余项R1(t)：

R1(t)=f(t)-c1(t)

(2)

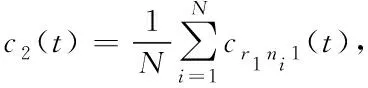
4) 重复3)得到

fnj-1(t)=Rj-1(t)+εj-1Ej-1(ni(t))

(3)

(4)

Rj(t)=Rj-1(t)-cj(t)

(5)

5) 直到获取的Rj(t)不超过两个极值点时，算法结束，Rj(t)即为最终的残余分量R(t)，最终f(t)表示为

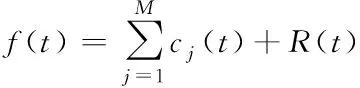
(6)

其中M为分解的IMF的数量，R(t)为残余分量。

3.2 Hilbert变换

对IMF分量信号进行Hilbert谱分析是脑电信号时-频域分析的有效方法，对CEEMDAN分解得到的IMF分量代入式(7)进行希尔伯特变换

(7)

得到解析信号zi(t)

zi(t)=ci(t)+jyi(t)=Ai(t)ejθi(t)

(8)

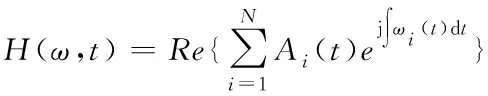
(9)

进一步求得希尔伯特瞬时能量谱(Instantaneous Energy Spectrum) IES(t)和边际能量谱(Marginal Energy Spectrum)MES(ω)：

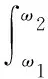
(10)

(11)

3.3 共空间模式特征提取

共空间模式算法的基本原理是利用矩阵的对角化，找到一组最优空间滤波器进行投影，使得两类信号的方差差异最大化，从而得到具有较高区分度的特征向量。算法具体流程如下：

1) 选取一次试验脑电数据构成N×T的矩阵EL或ER，其中N为通道数，T为一次试验采样点个数，EL表示左手运动的脑电数据，ER表示右手运动的脑电数据，由此得到协方差矩阵

(12)

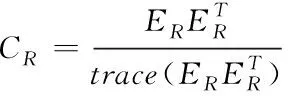
(13)

C=BΛBT

(14)

(15)

其中Λ是特征值矩阵；B是对应的特征向量矩阵。

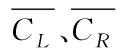
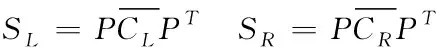
(16)

4) 对白化后的矩阵分别做特征值分解

SL=UΛLUTSR=UΛRUT

(17)

其中ΛL和ΛR是特征值矩阵，U是对应的特征向量。可证SL和SR的特征向量相等，ΛL与ΛR之和是单位矩阵，SL的最大特征值对应SR的特征值最小。

5) 由白化矩阵构造空间滤波器W

W=UTP

(18)

6) 对脑电信号滤波得到Z，进而得到特征向量fp

ZN*T=WN*NEN*T

(19)

(20)

其中var(X)是计算样本X的方差。

3.4 模糊熵

算法实现过程如下：

i=1，2，…，N-m+1

(21)

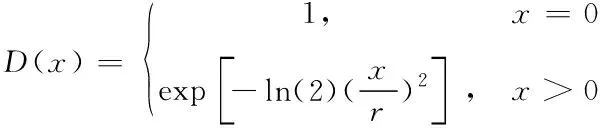
(22)

j=1，2，…，N-m+1，且j≠i

(23)

|u(j+p-1)-u0(j)|)

(24)

(25)

进而定义φm(r)和φm+1(r)

(26)

(27)

4) 因此可以定义时间序列的模糊熵FuzzyEn(m，r)为：

(28)

对于有限长的数据集，模糊熵估计为

FuzzyEn(m，r，N)=lnφm(r)-lnφm+1(r)

(29)

3.5 灰狼算法优化的支持向量机

支持向量机是在人机交互中识别生理模式的常用分类器，其具有多功能性、鲁棒性和免费专用工具箱的大量可用性等优点。SVM的目的是寻找一个超平面来对样本进行分割，分割的原则是间隔最大化，最终转化为一个凸二次规划问题来求解。c为惩罚参数，是调节分类间隔和误分类点个数的系数，c值增大时对误分类的惩罚增大，c值减小时对误分类的惩罚减小，最佳原则是使分类间隔尽量大，同时使误分类点的个数尽量小。核函数g的作用是与线性分类方法相结合来解决非线性问题，核函数的选择直接影响性能。本文中将两者相结合，利用灰狼算法选择SVM的最佳惩罚参数c和最佳核函数g，各等级狼的初始位置设置和狼群数量以及最大迭代次数分别设置为2，20，100。

4 实验

4.1 CEEMDAN分解

本文中将原始信号各通道直接CEEMDAN分解改进为设置时间窗滑动分解，时间窗设置为1s，信噪比控制系数ε为0.1，加入噪声的次数N为100次，原始4s的脑电信号由时间窗分割为4段分别进行CEEMDAN分解，在分解具有较高频率分辨率的基础上增加各时间窗上脑电数据的利用率。如图3所示，为某次试验C3通道和C4通道信号CEEMDAN分解的前5阶IMF分量及其频谱。可以看出各IMF分量的频率从高到底排列，后几阶IMF为低频，而运动执行相关电位的频率范围为8～30HZ，因此，本文试验中直接舍弃低频伪迹，可以看做是自适应高通滤波，使信号处理更加高效。为得到更准确的分析信号，对保留的IMF分量根据式(30)计算分量与原始分解信号的相关系数r(其中：c为IMF分量，x为原始信号，n=128)，选取相关系数最大的分量做后续处理。

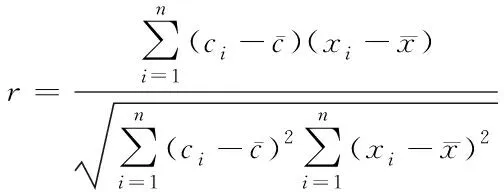
(30)

图3 C3和C4通道脑电信号CEEMDAN分解及其频谱分析

4.2 基于Hilbert变换的瞬时能量差和边际能量差特征提取

将选取的IMF分量进行Hilbert变换求取瞬时能量谱和边际谱。如图4所示，(a)为某次试验想象左手运动信号幅值变化，(a)为某次试验想象右手运动信号幅值变化，与想象左手或右手运动产生的事件相关去同步(event-related desynchronization，ERD)和事件相关同步(event related synchronization，ERS)现象相一致。图5为运动想象的边际谱，由图5可以看出左手和右手运动边际能量差异明显。因此选取C3和C4通道的瞬时能量差和边际能量差能更好的表示左手和右手运动想象特征。结合瞬时能量差和边际能量差得到时-频组合特征向量F1。

4.3 共空间模式(CSP)的特征提取

将CEEMDAN按时间窗滑动分解的IMF分量筛选和计算相关系数之后，保留每个时间窗分解后相关系数最大的IMF组合成新的多通道信号，记为X(IMFC31，IMFC32，IMFC33，IMFC34，IMFC41，IMFC42，IMFC43，IMFC44)。将组合而成的信号X经空间滤波器(spatial filters)W映射处理，得到空域特征记为F2。

4.4 模糊熵(FuzzyEn)特征提取

在想象左手和右手运动想象时，模糊熵衡量了C3和C4通道的信号序列复杂度。如图6所示，为100个样本中想象左手运动(a)和想象右手运动(b)的模糊熵值。本文为得到模糊熵特征，对每个通道信号计算模糊熵，嵌入维数m设置为2，将信号标准差归一化后的相似容限值r设置为0.15，计算结果组合成特征集F3。

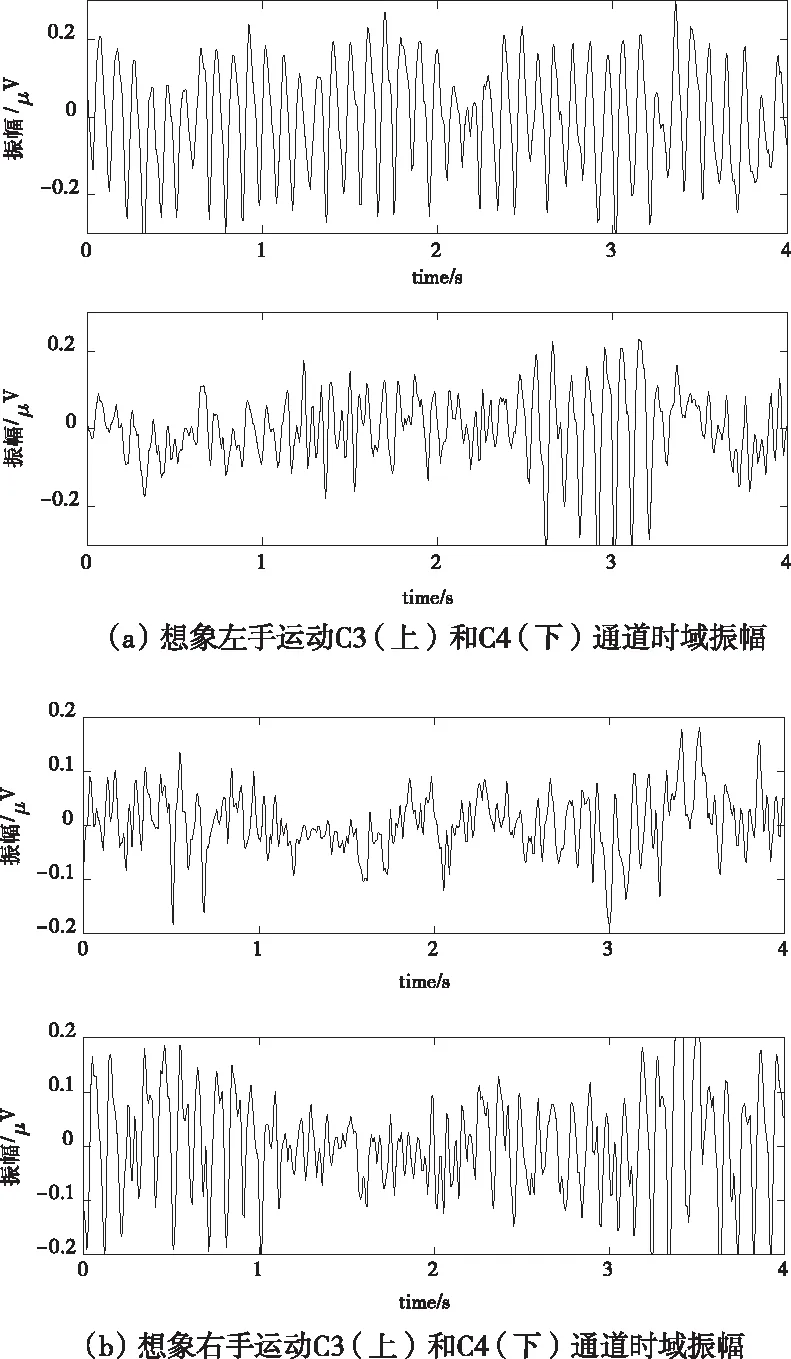
图4 想象左手和右手运动C3和C4通道时域振幅对比

图5 想象左手和右手运动C3和C4通道边际谱对比

图6 想象左手和右手运动C3和C4通道模糊熵值对比

4.5 实验结果与分析

将所有特征集组合成18维特征F={F1，F2，F3}，输入到GWO-SVM分类器进行分类，各单一特征和组合特征的分类结果见表1。

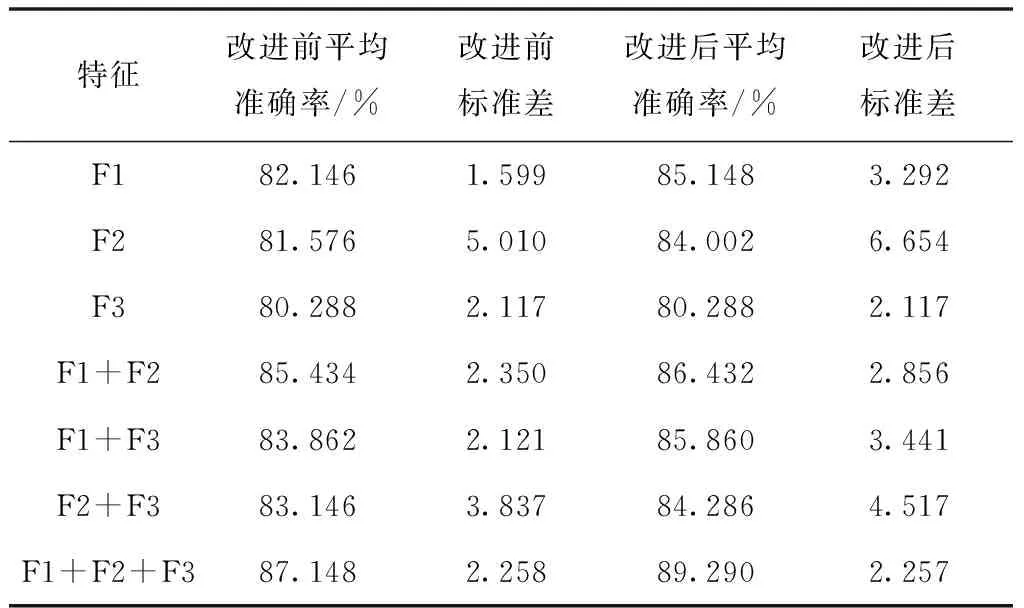
表1 分类结果对比

由平均分类准确率可以看出组合特征结果明显高于单一特征，加时间窗改进CEEMDAN分解后的正确率也高于未改进。融合特征的准确率更高，验证了多种方法的融合特征可以对单一特征弥补不足，是提高分类正确率的重要思路。多种特征融合的分类准确率中，加时间窗改进处理比未改进提高了2.142%；在所有与CEEMDAN分解相关的特征分类中，平均分类准确率平均提高了1.673%；其中，特征F1和特征F2分类正确率提高最高，分别为3.002%和2.426%，说明加时间窗分解的方法在一定情况下相当于将两通道数据增加为多通道，可以进一步提高分类正确率。为描述多次试验结果的波动，选用和数据单位一致的标准差来衡量。对于改进后的单一特征和两两特征融合，虽然提高了分类正确率，但是结果波动相比更大，而改进后的多特征融合的方法在提高正确率的基础上标准差几乎没有变化甚至略微减小，结果具有较强的稳定性。因此，加时间窗改进后的多特征融合方法对运动想象脑电信号分类正确率的提高具有重要意义。

5 结论

本文引入CEEMDAN方法应用于运动想象脑电信号特征提取，对BCI Competition II数据集进行处理分析，在对信号CEEMDAN分解时加时间窗滑动改进处理，并结合时-频-空域-非线性动力学模糊熵的多特征融合的方法进行组合分析，融合特征的分类正确率达89.290%，改进后的方法对正确率提高了2.142%，结果表明改进的CEEMDAN分解方法可以提高分类正确率而且具有更高的稳定性。因此，多特征融合的方法将各单个方法的缺点互补，进一步提高分类正确率，为脑电信号模式识别研究提供了一种新的识别方法和研究思路。下一步的研究将引入其它新的机器学习方法应用于脑电信号处理，将继续研究多特征融合来进一步提高脑电信号分类正确率。