数学沉浸式学习环境的设计与实现

纪海林，刘语柔，叶心怡，骆岩林

(北京师范大学人工智能学院，北京 100875)

1 引言

数学作为认识世界的基础学科，它是一门自然科学，更是一个可以支持其它学科深入发展的工具[1]。学习者在学习数学知识的过程中，经历数学训练之后习得的数学思想和逻辑思维能力，无时无刻不在对学习者的未来发展产生积极的作用。考虑到人的认知特点，注重学习者的主体地位和个性发展，运用一定的教育技术手段改革传统学习方式来传播数学知识，对一般学习过程进行干预，对于学习者来说是非常重要的。

目前，使用VR开展的沉浸式学习日益受到各方的重视。在英国开放大学发布的《2018年学习趋势报告》中，沉浸式学习被列为未来学习趋势的重要方向[2]。传统的学习模式已经不能满足学习者获取知识的渴望，并在一定程度上限制了学习者创新性思维的发展，大大阻碍了它们的主观能动性。VR技术与教育教学领域的结合，能够给学习带来沉浸式的新体验，在很大程度上弥补书本文字的缺陷，具有三维立体交互的优势。通过虚拟现实构建的沉浸式学习环境，可以结合学科内容呈现逼真的场景，调动学习者的积极性，从而产生更加沉浸和难忘的学习体验，促进学习效果的提升。

2 沉浸式学习

随着计算机仿真技术的快速发展，结合心理学界的沉浸理论和教育学领域的沉浸式教学，沉浸式学习(Immersive Learning，IL)开始结合计算机技术适用在各种形式的学习场景中，它是指通过使用虚拟现实、增强现实、混合现实及扩展现实等各类技术，为学习者营造具有极强真实感且无外界干扰的新环境，在这个环境中，学习者可与各种对象进行复杂或多元的交互[3]。徐铷忆等[4]论述了沉浸式学习体验对于学习者的认知、动作技能、情感和思维训练四个方面的促进作用。沉浸式学习可以让传统方式无法实现或者难以再现的场景成为可能，可以创设身临其境的感官体验，提供丰富多元的交互体验，把学习者学习过程中的被动感转化为自主性和主动性，沉浸式学习的模式对于激发学习兴趣、拓展创造性和发散性思维有着极大的促进作用[5]。

伴随沉浸式学习的日益拓展，跨学科的结合促进了其各方面的探索。以“沉浸式学习”为主题在CNKI检索近20年的相关学术期刊，如图1可以看出相关文献数量整体呈上升趋势，并且在近五年得到飞速发展，说明沉浸式学习成为越来越受到关注。

图1 沉浸式学习研究趋势

虚拟现实引入沉浸式学习从技术层面来说是具有合理性和可行性的。其所使用的沉浸式虚拟现实技术是通过计算机和VR设备呈现近乎真实的三维虚拟环境，让用户获得多感官的体验，同时用户可以和虚拟环境进行自然交互，对用户的操作生成设定的反馈[6]。沉浸式虚拟现实对教育的影响体现在提升学习体验上，它能够支持沉浸式学习、交互式学习以及高效率学习[7]。一方面沉浸式虚拟现实可以满足学习者的视觉、听觉甚至触觉等多个感官通道，多维感官刺激有助于提升学习效率。另一方面它阻隔了学习者与外部世界的感官联系，让学习者可以在与学习内容交互的过程中产生沉浸感，阻绝外界环境的影响因素以避免走神，这是高效率学习的前提。

在数学领域，在文献库中以“沉浸式学习”和“数学”为关键词进行相关论文的检索，仅有10篇论文，实际相关的论文仅有不到5篇(截至2022年4月1日)。可见目前在数学领域的沉浸式学习研究还很稀少单调，大都局限于对数学公式的图形可视化和几何图形变换的数学模型上，缺乏自然交互和沉浸感。例如，江绘良等[8]提出的虚拟现实在数学教学领域的应用主要围绕将抽象的曲线曲面实现三维图形的绘制。但刘超等[9]认为现代教育技术深入融合到学习中是必然的趋势，有利于学习者理解抽象数学知识，提高学习者的学习主动性，营造良好的学习氛围，提升学习效果。表明以运用虚拟现实的沉浸式学习方式在数学领域还有着广泛的应用前景和探索空间。

沉浸式学习环境(Immersive Learning Environment，ILE)是指应用计算机仿真技术如虚拟现实等构造的具有高度沉浸感的虚拟仿真学习环境，让学习者完全沉浸于知识获取的过程中，如同体验真实的学习环境。Hedberg等[10]认为虚拟环境有理由要增强逼真性和沉浸感以提供更好的学习体验。仇晓春[11]认为虚拟环境中的高度的浸入感和强烈的存在感依赖于虚拟环境的逼真性和交互能力。因此，虚拟环境在运用VR构建成为沉浸式学习环境的过程中，它的逼真程度和学习者在其中的自然交互体验非常关键。

总体而言，沉浸式学习环境的构建很大程度上影响了基于VR的沉浸式学习带给学习者的交互体验和学习效果。因此，本文提出构建以数学为主题的沉浸式学习环境，重新塑造数学学习方式，有效提升学习效果。

3 沉浸式学习环境设计

本文结合中国科技馆的“数学之魅”主题展区中的“滚出直线”、“莫比乌斯环”和“立体四子棋”三个展项，运用虚拟现实技术对其进行建模和交互设计，构建相应的沉浸式学习环境，进而给出沉浸式学习环境的总体框架和实践应用成果，如图2所示。最低层的数据层记录系统内的全部数据，通过逻辑层的传输，传递给渲染层完成模型展示和场景渲染，交互层作为接口，提供一系列功能，与用户进行实时交互。

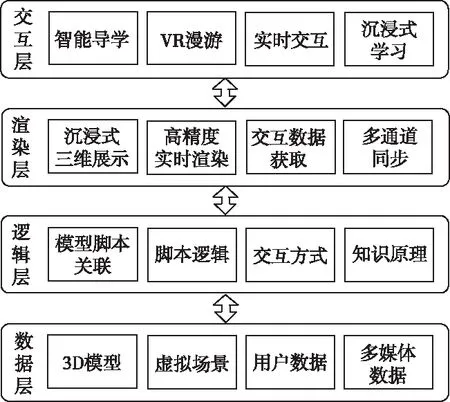
图2 数学沉浸式学习环境框架

数学学习内容包括以下三个具体展项：

1) 滚出直线

滚出直线展项中，在展台上的上方是一个小圆齿轮内切于一个大圆齿轮，小圆齿轮的直径等于大圆齿轮的半径。该科普展项的原理：如果把一个圆放在另一个两倍于它直径的大圆内作纯滚动时，小圆圆周上任意点的运动轨迹是一条直线，即该点作直线往复运动。当参与者使用手柄按下按钮时，小圆齿轮在大圆齿轮中滚动两周，同时带动两辆小汽车沿着固定的直轨道进行运动。这件展品以直观生动的形式，展示数学原理，体现数形结合的思想。

2) 莫比乌斯环

莫比乌斯环展项中央有一个巨型的圆环，在圆环上有一辆小车。当参与者使用手柄触碰到小车时，小车开始移动，在转动一圈之后，小车能够回到原点。中间巨型的圆环是莫比乌斯环，只有一个面一条边，因此小车从环上任意一点出发最后都能回到原点。该展项以直观动态的形式，展现莫比乌斯环的奇妙之处。

3) 立体四子棋

立体四子棋是由棋子空间矩阵构成的立体棋盘。游戏双方通过操作台上的按钮，调整棋子在三维坐标上的位置。某一方先将四个相同颜色的小球连成一条直线者赢。这件展品可以通过游戏的形式来锻炼参与者的空间想象能力和立体思维能力，帮助学生更好地想象数学中的空间立体几何，加深对空间直角坐标系的理解和运用。

4 关键技术

4.1 建模与动画设计

以“莫比乌斯环”为例，如下为Blender中的建模过程。

首先完成基础模型对象立方体和贝塞尔圆环的创建，并对其做相应调整，删除多余表面。对立方体对象依次添加四个修改器：阵列修改器、简易形变修改器、曲线修改器和表面细分修改器。对应完成基础对象副本创建，整体模型扭曲变形和成环拼接，以及表面光滑和细化。为了逼近真实展项，再添加简易形变修改器，不断调整扭曲和弯曲的角度和轴向，最后模型效果如图3所示。

下面介绍Blender中的动画设计过程。

首先，在编辑模式下，得到基础模型对象上下表面的中心线段，通过删除多余顶点和副本线段的拼接，得到目标路径曲线。导入已建好的小车模型，调整小车对象局部坐标原点后，添加物体跟随路径约束，初步生成小车沿曲线路径运动的动画，如图4所示。在动画编辑窗口下，根据莫比乌斯环的实际轨道角度变化调整小车对象的角度变换，在相应位置插入关键帧，使其动画效果与实际相符，防止小车对象运动过程中产生穿模现象。

图3 莫比乌斯环变形 图4 设置小车动画

在实物图片和模型草图的基础上进行仿真建模，保持原有模型的关键特征和比例，真实还原模型的结构、形状和各个组成部分，最后导出为FBX格式文件，包含相应的模型和动画。

4.2 系统搭建

在初步模型的基础上给物体对象添加材质贴图，以逼近真实场景中的视觉效果，最终搭建得到的数学沉浸式可视化场景如图5、图6和图7所示。学习者可以利用VR头戴式设备进入虚拟环境，通过操控手柄与虚拟对象进行互动，定位器会计算头显和操控手柄在有限区域内的位置，实现场景自主漫游。

同时学习者在交互过程中，系统提供关于操作方法的提示与相关知识点的指导，系统将自动感应学习者的位置以控制讲解声音的播放。加入声音解说与展板，丰富系统的交互方式，增强沉浸感。

图5 滚出直线

图6 莫比乌斯环

图7 立体四子棋

4.3 交互设计

交互设计是项目的核心部分，下面着重介绍三个案例的关键交互逻辑。

4.3.1 “滚出直线”的交互设计

滚动原理为，小圆以既定的速度v的绕大圆的中心点顺时针公转的同时以速度为2v进行逆时针自转。由此即可带动两辆小汽车在轨道上运动，但同时还需要限制小汽车的自转运动，才能实现小汽车朝向不变的直线往返运动。所以为了克服小汽车的自转，给小汽车加上一个顺时针的自转，刚好抵消小圆齿轮转动带给小汽车的逆时针自转。具体的逻辑实现如下所示。

算法1：“滚出直线”的逻辑实现

变量说明：

flag：为1，表示选中按钮，开始播放18秒的动画；

为0，表示取消选中按钮，停止播放动画。

timer：计时器，数值表示经过的秒数

伪代码：

1)function Update()

2) if 玩家选中按钮：

3) flag=1；

4) 播放齿轮运动声音；

5) if flag==1：

6) if timer <=18：

7) 大圆盘绕中心点公转；

8) 小圆盘绕中心点自转和公转；

9) 小车绕中心点自转和公转；

10) 小车反向自转；

11) timer+=Time.delTime；

12) else：

13) timer=0；

14) flag=0；

15)end function

4.3.2 “莫比乌斯环”的交互设计

在导入模型的展开资源里面找到相应的动画，将其拖拽到对应的模型上并设置动画播放参数，通过脚本控制动画的播放。具体的实现如下所示。

算法2：“莫比乌斯环”的逻辑实现

变量说明：

count：玩家选中小车的次数，奇数播放动画，偶数停止播放

伪代码：

1)function Update()

2) if 玩家选中小车：

3) if count % 2==0：

4) 播放小车动画；

5) else：

6) 停止播放小车动画；

7) count++；

8)end function

4.3.3 “立体四子棋”的逻辑实现

在“立体四子棋”中，玩家可以进行交互，选择“人机”或“双人”模式。为了使代码逻辑清晰，将主体分为四大部分，并定义变量model。当model=1时进入选择部分，当model=2时进入人机部分，当model=3时进入双人部分，当model=4时进入重置部分。

在选择模式中，首先设置计时器，同时为了防止计时爆掉，每秒都重置为0。变量model=1时进入选择模式，根据手柄射线反馈选中“双人”或“人机”按钮进入对应的对战模式。具体实现如下所示。

算法3：选择模式的逻辑实现

变量说明：

renewTime：重置计时器

hitObj：玩家手柄射线击中的物体

buttonNum：表示模型上对应的选项按钮，每名玩家对应9个

伪代码：

1)function SelectionMode()

2) renewTime=0； ∥ 计时

3) 获取射线击中的物体赋予hitObj；

4) if hitObj的父对象==“FourChess”：

5) 将hitObj的名字转为整型赋给buttonNum；

6) if buttonNum % 9==1：

7) model=2； ∥ 进入人机对战

8) else if buttonNum % 9==2：

9) model=3； ∥ 进入双人对战

10)end function

在人机模式中，由于棋盘的大小很有限，使用的算法是基于固定的打分机制，对每个落子位置进行打分，从而得到最优解。

在正式进入下棋游戏后，Examine函数检查是否已有四个同色棋子连成直线，并更新路径的状态。同时机器下棋时，调用AssessWayChange函数对每条路径的通道分别进行计算，再调用AssessBall函数对每个棋子的通道分求和，并返回权重最大的棋子索引，以确定机器的落子。

如果已有四个同色棋子连成直线，则显示获胜球路径和获胜方，并置model为4。但如果棋子下完之后依然没有四子连珠，则表示和棋，不显示获胜球路径和获胜方，也置model为4。

具体的逻辑实现如下所示。

算法4：人机模式的逻辑实现

变量说明：

hitObj：玩家手柄射线击中的物体

buttonNum：表示模型上对应的选项按钮，每名玩家对应9个

playerBall：玩家落子位置

伪代码：

1)function P2cMode()

2) 获取射线击中的物体赋予hitObj；

3) if hitObj的父对象==“FourChess”：

4) 将hitObj的名字转为整型赋给buttonNum；

5) if buttonNum % 9==3 && 选中位置可下棋：

6) outcome=Examine(playerBall)；

7) if outcome！=-100： ∥ 玩家胜利

8) 显示获胜球路径和玩家胜利；

9) model=4； ∥ 进入重置模式

10) return；

11) else： ∥ 机器开始下棋

12) AssessWayChange()； ∥ 计算权重

13) machineBall=AssessBall()； ∥ 决策

14) if machineBall==-100： ∥ 无棋可下，和棋

15) model=4；

16) return；

17) 机器落子；

18 outcome=Examine(machineBall)； ∥ 检查落子

19 if outcome！=-100： ∥ 机器胜利

20) 显示获胜球路径和机器胜利；

21) model=4；

22) return；

23) player=1； ∥ 下一次玩家下棋

24) else if 12 < buttonNum < 19 ‖ 3 < buttonNum < 10：

25) 根据buttonNum移动选中的球；

26)end function

在双人模式中，下棋步骤与人机模式相同，不同的是该模式下在两侧的操作台分别代表不同的红蓝方，而人机模式中默认机器为红色方。这时两端的操作台交替进行下棋，只有轮到其中一方下棋时，该方的操作台按钮可以进行棋子移动和确定落子。其具体实现不再展示。

在重置模式中，等待获胜球路径显示一段时间后，将重置所有棋子颜色以及相关的变量，清空权重的存储，实现模型所有组件的初始化，游戏重新开始。

5 评价实验与分析

本次评价主要从感官体验、交互体验、情感体验三个方面设计评价实验和问卷，以探讨沉浸式学习环境的效果和改进方向。

5.1 问卷设计

评价实验的对象是校内的15位大学生，在前期研究对象筛查中，主要调查了参与者是否曾经有过虚拟现实(VR)体验。调查结果显示在这15个人中，只有1人经常体验虚拟现实设备，因此此次问卷填写的对象具有一定的参考意义。

本次评价设置的问题分别为感官体验、交互体验、情感体验三个方面。感官体验对于学习者来说是体验基础，是最直接的体验，是虚拟环境呈现的视听体验，主要涉及学习者是否产生真实感和沉浸感。交互体验对产生真实感和沉浸感至关重要，关键在于系统的简单可用性。情感体验涉及到是否顺利达到目标、是否愿意再探索等情绪因素，是呈现给学习者心理上的体验，关键在于系统是否友好和人性化。

因此依据Tcha-Tokey K等[12]提出的有关沉浸式虚拟环境中用户体验的统一调查表，结合系统需要，建立调查问卷。每题均采取10级里克特量表，1为非常不赞同，10为非常赞同。详细调查结果见表1。

表1 问卷调查结果

5.2 结果分析

为了考察参与者在沉浸式学习环境的体验受以往虚拟现实经验的影响程度和方面，对从未有VR体验的样本和偶尔有VR体验的样本进行独立样本t检验。Sig.(双侧)的值小于0.05时表示差异性显著。检验结果中，从未有VR体验的样本和偶尔有VR体验的样本的Mean(S.D.)分别为6.00(1.414)和6.67(2.348)，T值为0.382，Sig.(双侧)为0. 474。以上检验结果表明参与者在沉浸式学习环境的体验受以往虚拟现实经验的影响不大，虚拟环境对于初学者很友好，方便上手使用和体验。

通过对所有问题的得分进行均值计算，结果如表5所示，表明参与者对虚拟环境的视觉体验较好，并认为视觉效果、声音和交互设备对沉浸式学习有很大的影响，参与者的沉浸感较好，而且参与者在虚拟环境中的学习体验较好，同时参与者在虚拟环境中不易感觉到紧张、被动、疲惫和眩晕，交互设计人性化。由此可见沉浸式学习环境的构建达到了初步目标。

通过计算每个维度的平均得分，分析参与者对于各个维度的体验感。如图8所示，感官体验和交互体验两个维度获得较高分，表明参与者在系统中获得良好的视听体验，并认为系统简单可用，但其在人性化和友好性方面有待加强。总体而言，参与者有较好的沉浸式体验。然而，受设备硬件的影响，本项目还需设计更人性化的交互界面来改善用户体验；此外，还需通过利用更高性能服务器，使得系统更加流畅和清晰，从而增强体验者的沉浸感。

图8 问卷各维度结果分析图

6 结语

以实体科普场馆为依托，沉浸式数学学习环境是其多维度功能拓展和延伸，更注重体验式、探究式学习，两者有机结合，科普效果优于仅通过实体展项的传播方式。本文以中国科学技术馆“数学之魅”展区的“滚出直线”、“莫比乌斯环”和“立体四子棋”三个展项为例，给出相应的环境建模和交互设计，并加入文字、声音等导航方式，构建数学沉浸式学习环境。运用多感官、沉浸式、逼真的方式实现学习环境，让学习者能够身临其境般地进行体验学习。同时，可以摆脱时空的束缚，是对学习方式的一种新的尝试，更能激发数字学习模式的创新。

本文所实现的沉浸式数学学习环境所涵盖的学习内容体系还不够完善，未来有待加入力觉交互和在线访问功能，实现更广泛的沉浸式学习。由于数学学习内容的特殊性和持续性，再加上虚拟现实、扩展现实等技术昂贵的设备成本和复杂的体验模式，这些技术在教育方面的使用没有实现真正的普及，没有能够进入普通民众的现实生活。但希望随着计算机仿真技术的发展和设备生成制造费用的降低，沉浸式学习将成为未来学习方式的趋势，促进学习者在虚拟环境中进行探索性学习并通过具象的方式加深对抽象知识的认知和实践经验的积累。