基于模糊MRAS的高速永磁同步电机转速观测
何延昭,王贞艳,郭炎龙,王金霞
(1. 北京轩宇空间科技有限公司,北京 100190;2. 北京控制工程研究所,北京 100190;3. 太原科技大学电子信息工程学院,山西 太原 030024;4. 河南卫特机器人有限公司,河南 郑州 450000.)
1 引言
高速永磁同步电机(High Speed Permanent magnet Synchronous Motor,HSPMSM)具有体积小、重量轻、效率高、动态响应快、转矩脉动和噪声小等优点小[1],在航空航天领域尤其是动量轮、控制力矩陀螺等空间机构设计有广阔应用价值。HSPMSM转速可以达到每分钟上万转,无需增速箱,与高速负载直接相连,提高整个系统的运行效率同时节约成本。矢量控制技术是永磁同步电机常用的驱动方式,要实现对电机的高精度、高效率的速度和位置控制,一般需要采用传感器。传感器的使用通常会增加电机的成本和体积,并且降低系统的可靠性[5]。因此,对高速永磁同步电机进行无传感器控制研究是很有必要的。
高速永磁同步电机相比于普通永磁同步电机,其高速高频的特点需要无传感器控制算法转速估算收敛快。模型参考自适应算法(Model Reference Adaptive System,MRAS)因其结构简单、算法较简单[6]、计算复杂度低、易于在数字控制系统中实现并且系统稳定性有理论收敛证明而被广泛采用[7]。Pradeep Kumar在文献[9]中采用MRAS算法进行了转速固定负载变化、转速变化负载固定以及转速负载同时变化下的无传感器矢量控制,仿真结果表明该算法具有强的鲁棒性。文献[10]在分析MRAS原理的基础上,对传统PI、模糊PI以及粒子群优化控制算法进行了对比分析,得出MRAS的适用性很强。文献[11]分别采用李雅普诺夫稳定性和波波夫超稳定型分析法构建了自适应律,并对其进行分析,得出在实际系统中,波波夫超稳定型分析法比李雅普诺夫方法具有更好的性能。文献[12]运用现代控制理论知识分析了MRAS系统的稳定性,在构建系统传递函数的基础上对其进行分析,并且辨识出来系统电阻参数值。文献[13]在文献[12]的基础上,采用根轨迹分析法对自适应律中比例积分系数进行分析整定。文献[14]在MRAS理论的基础上,将学习效率和性能更为突出的径向基函数神经网络与模型参考自适应系统(MRAS)相结合,通过神经网络调节两个模型的误差信号进而得出转速估计值,故而精度较高,动、静态性能好。
从上述研究来看,使用MRAS估计转速的关键在于可调模型的建立以及自适应机构中自适应律的构建,自适应律的好坏直接决定着估计转速的精度和系统的稳定性。传统的方法中,通常选用比例积分(proportional integral,PI)的形式。随着国内外对此方法研究的不断深入,目前已有多种PI参数的整定方法,同时也有将模型参考自适应与其它控制算法相结合,代替传统自适应律中的PI。自适应律通常选用PI调节器结构,动稳态性能往往只能保证在一定的速度范围内调整为最佳[15]。高速永磁同步电机的调速范围宽,基于传统PI的模型参考自适应观测器(PI-MRAS)性能难以满足要求。文献[17]为使得HSPMSM在全转速范围内都能取得满意的控制效果,对传统MRAS自适应律中固定的比例积分参数值进行分段选取;张洪帅在文献[15]中为了使MRAS在高速永磁同步电机整个控制过程都能起到较好的控制效果,将模糊控制应用到比例积分自适应律中,用模糊控制对PI参数进行动态调节;文献[14]提出了一种将学习效率和学习性能更为突出的径向基函数神经网络(Radial Basis Function Neural Network,RBFN)与MRAS相结合,该方案只需要q轴估计电流和q轴实际电流之间的误差信号,然后利用RBFN调节器对误差信号进行调整,得到估计的速度;文献[18]将一个动态调整器添加到MRAS估算转速的反馈环节,以此来减少扭矩和转速的波动;文献[19]在直接功率控制(Director Power Control,DPC)技术基础上,利用人工神经网络,提出了一种新颖的模型参考自适应系统(MRAS)速度观测器,该MRAS速度观测器采用电流模型作为自适应模型。然后利用反向传播网络(BPN)算法对神经网络进行在线设计和训练。
本文利用改进MRAS对高速永磁同步电机转速进行观测。首先介绍了传统的MRAS转速观测器设计,在详细介绍模糊控制技术的基础上,将模糊控制用于模型参考自适应控制系统中,采用双输入单输出的模糊控制结构取代常规的PI自适应控制律,实现风机类负载工况下电机转子位置和转速的估算。最后,仿真结果证明了上述方法的可行性和有效性。
2 模糊MRAS的HSPMSM转速观测器
2.1 表贴式高速永磁同步电机数学模型
研究对象为表贴式HSPMSM。为了方便后期控制器的设计,通常选择同步旋转坐标系d-q下的数学模型。在建立数学模型之前,需做如下假设:①忽略定、转子铁芯磁阻,不计涡流和磁滞损耗;②永磁材料的电导率为零,永磁体内部的磁导率与空气相同;③转子无阻尼绕组;④永磁体产生的励磁磁场和三相绕组产生的电枢反应磁场在气隙中均为正弦分布;⑤稳态运行时,相绕组中感应电动势波形为正弦波。
定子电压方程
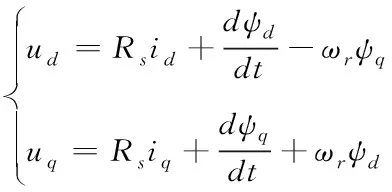
(1)
式中:ud、uq为定子电压d、q轴分量;Rs为定子等效电阻;id、iq为定子电流d、q轴分量;ψd、ψq为定子磁链d、q轴分量;ωr为转子电角速度。
定子磁链方程

(2)
式中:Ld、Lq为定子电感d、q轴分量;ψf为永磁体磁链。将(2)式代入(1)式,可得定子电压方程为

(3)
电磁转矩方程

(4)
式中:Te为电磁转矩;pn为极对数。
2.2 传统模型参考自适应转速观测器
根据模型参考自适应的原理,这里选择HSPMSM本身作为参考模型,选择含有电机角速度ωr的电流模型作为可调模型,两模型具有相同物理意义的输出id和iq。依据两个模型输出的误差,通过自适应算法来对可调模型的参数进行调整,由此得到转速估计值。
将(3)式中d、q轴电流id和iq作为HSPMSM的状态变量,得其电流模型为
(5)
对于表贴式HSPMSM来说,Ld=Lq=Ls,所以式(5)可改写为
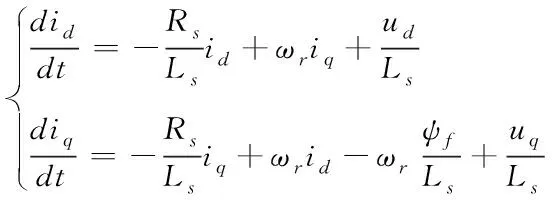
(6)
则其可调模型为

(7)

根据波波夫(Popov)超稳定性定理,可以得到观测转速的表达式为

(8)


图1 MRAS转速观测器原理图
3 模糊控制技术在MRAS中的应用
3.1 模糊MRAS系统设计
在常规的MRAS系统中,可调参数由自适应PI调节器来调节。本文在文献[4][20]的基础上,采用一种基于二维模糊控制器的模型参考自适应系统,用二维模糊控制器进行非线性最优控制,进而最小化电流误差。图2为基于模糊控制技术的模型参考自适应控制系统(简称Fuzzy-MRAS)
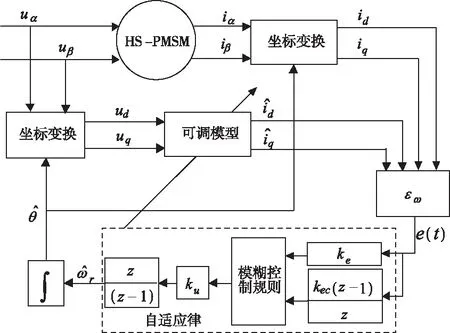
图2 Fuzzy-MRAS转速观测器原理图
图2中虚线框部分为模糊自适应律部分,首先定义电流误差e(t)为
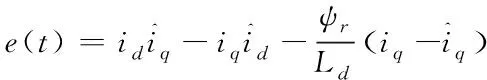
(9)
模糊控制器的输入为e和ep(其中e为文中定义的电流误差,ep为电流误差的变化率,ep=de(t)/dt)经过模糊化后的量,输出为控制量增量Δu,解模糊化后作为电机转子角速度增量Δωr。
模糊控制器的输入量化因子ke、kec和输出比例因子ku的选择会影响整个模糊逻辑控制器的控制性能。本文通过误差调整来对上述量进行整定以保证整个模糊控制器的性能。
3.2 模糊控制规则设计
模糊控制器输入和输出隶属度函数均采用三角形函数。图3为二维模糊逻辑控制器的输入e和ep的隶属度函数,在输入论域上定义7个模糊子集:{NB,NM,NS,ZE,PS,PM,PB},其中NB为负大(negative big),NM为负中(negative medium),NS为负小(negative small),ZE为零(zero),PS为正小(positive small),PM为正中(positive medium),PB为正大(positive big)。图4为二维模糊逻辑控制器的输出的隶属度函数,其中模糊控制规则设计如表1所示。

图3 模糊控制器输入e和ep隶属度函数

表1 模糊控制规则

(10)
式(10)中μ为控制器增量的隶属度函数。电机电角速度和位置估计为

(11)

(12)
式(11)、式(12)中ku为控制器输出比例因子,Ts为采样周期,θ(0)为转子初始位置。

图4 模糊控制器输出估算转速变化率隶属度函数
4 仿真及结果分析
为了验证本文所提观测方法的有效性,基于MATLAB 2014a仿真软件,在Simulink环境下搭建了系统仿真模型,对基于模糊MRAS的表贴式HSPMSM无速度传感器矢量控制进行了仿真研究。仿真所用HSPMSM模型为Simulink内部提供,被测HSPMSM在20℃时参数如表2所示,仿真设定时长为10秒。矢量控制系统中转速环和电流环控制器采用增量式PI控制器,电机控制系统原理框图如图5所示。
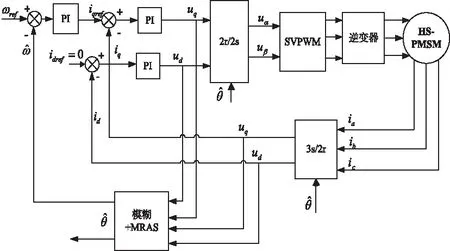
图5 基于Fuzzy-MRAS的HSPMSM无速度传感器矢量控制原理图
仿真所用的电机参数为R=0.122Ω,L=0.675 mH,ψf=0.0406Wb,J=0.00179kg·m2,极对数p=2。
图6为负载变化时,采用本文所述方法的仿真波形。电机稳态时转速给定值为30000r/min,电机给定转速在4秒时达到30000r/min。电机载荷在6秒之前为叶轮性载荷(转矩与转速平方成正比),转速稳定时载荷为3.6N·m,在6秒时电机载荷突变到5N·m,并在8秒时恢复为3.6N·m。图6(a)和(b)分别为实际转速与观测转速波形以及两者之间的差值,可以看出,实际转速和估测转速在稳态时趋于吻合,只是在扰动出现的瞬间转速有波动,表明本文所提转速观测器有较强的抗干扰能力;图6(c)为相应状态的电磁转矩波形。
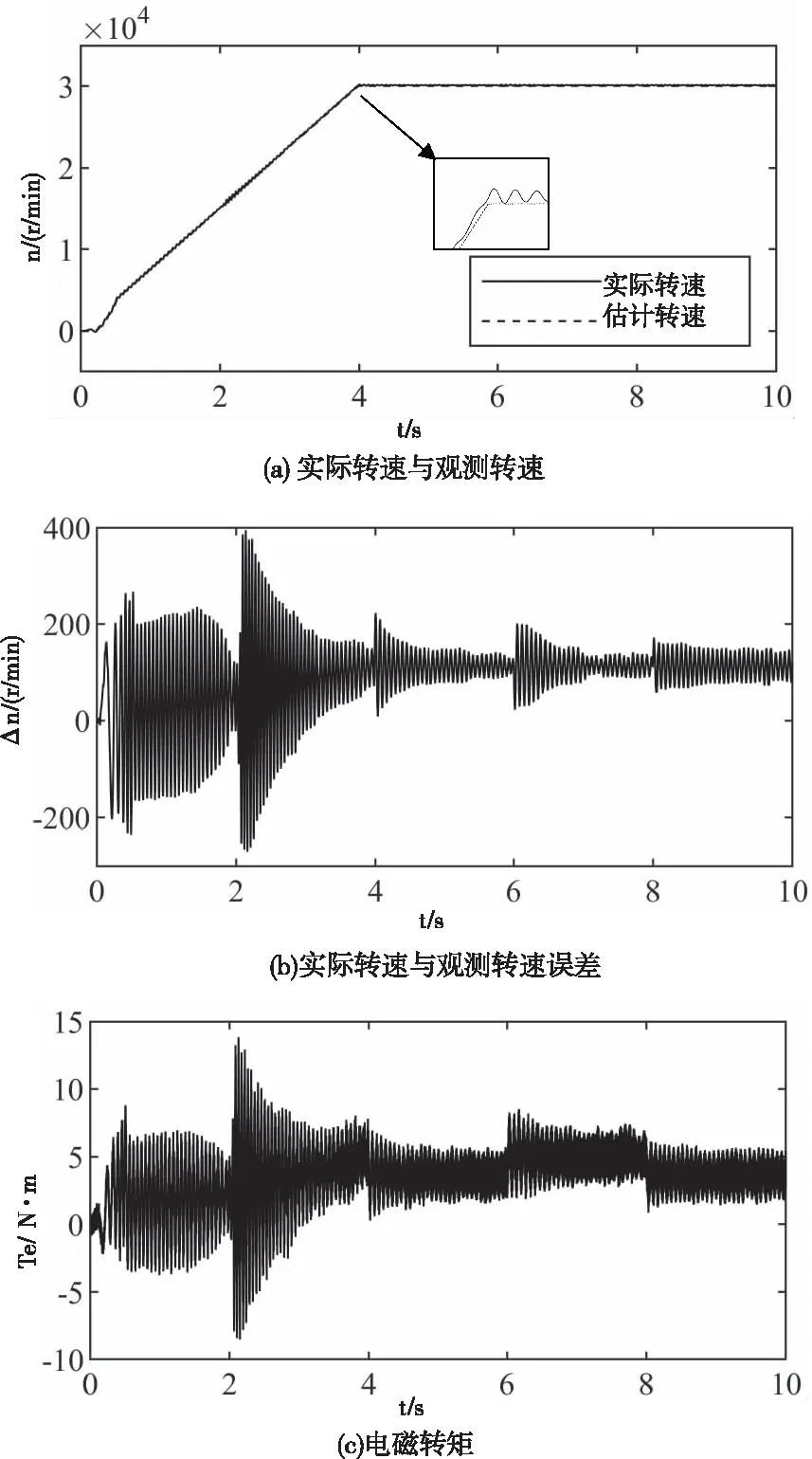
图6 HSPMSM变负载工况下仿真研究波形图
图7为转速变化时,采用本文所述方法的仿真结果。电机在6秒之前稳态时转速给定值为30000r/min,在6秒时将转速给定设置为20000r/min,8秒钟时电机转速给定又恢复为30000r/min。仿真结果如图7所示,图7中(a)和(b)表明,估测转速能够很好的跟踪实际转速,图7(c)为相应情况下的电磁转矩。
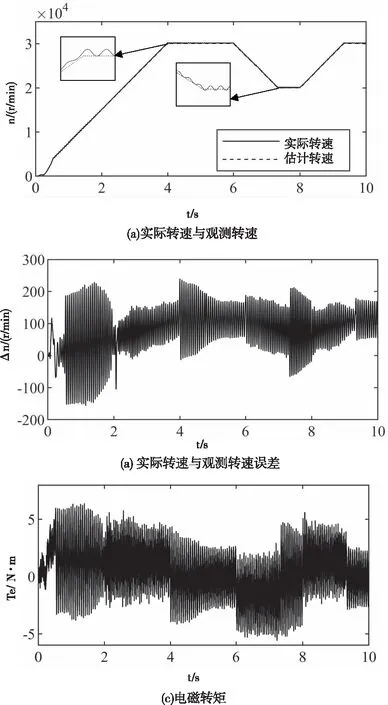
图7 HSPMSM变转速工况下仿真研究波形图
图8为变转速变载荷情况下的仿真波形。电机在6秒之前稳态时转速给定值为30000r/min,在6秒时将转速给定设置为20000r/min,8秒钟时电机转速给定又恢复为30000r/min;电机载荷在6秒之前为叶轮性载荷(转矩与转速平方成正比),转速稳定时载荷为3.6N·m,在6秒时电机载荷突变到5N·m,并在8秒时恢复为3.6N·m。由图8(a)和(b)可以看出,本文所提观测方法对扰动能做出较快反应,鲁棒性强。
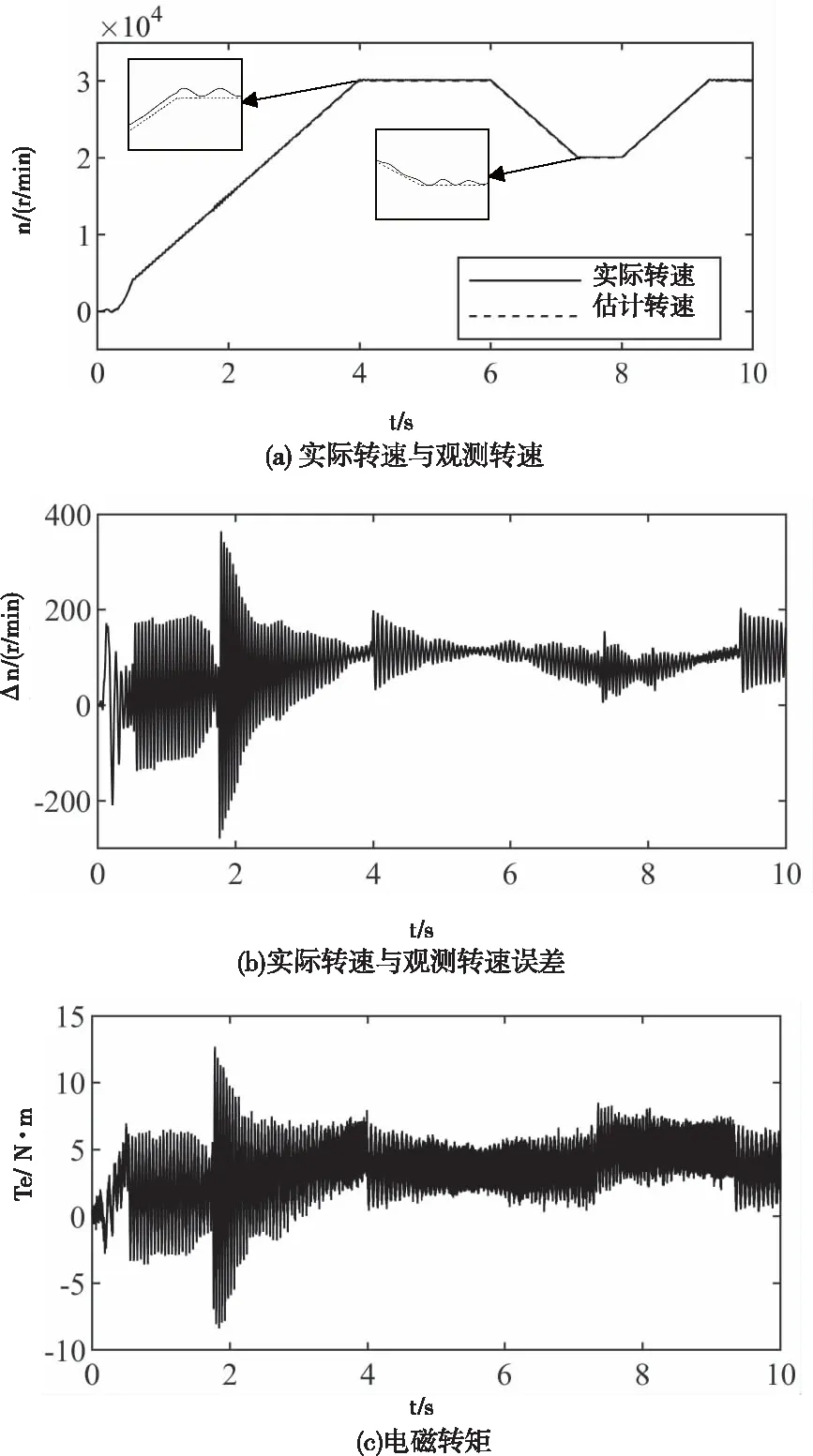
图8 HSPMSM变转速变负载工况下仿真研究波形图
4 结论
本文提出了模糊 MRAS 速度观测方法,将HSPMSM 本体作为参考模型、电流模型作可调模型。并利用模糊控制器替代 MRAS 中传统的 PI 控制器,采用二维模糊控制结构:将电流误差和误差变化经模糊化后作为控制器的输入,输出为控制量增量,解模糊化后作为转子电角速度增量。本策略在电机负载转矩变化、转速变化、变转速变负载等变化情况下的仿真研究表明:系统动态、稳态性能良好,对转速变化及负载转矩波动具有较强的鲁棒性。

