考虑保守卖空与财务困境的背景风险投资组合模型
刘勇军, 李莹莹, 张卫国
(华南理工大学 工商管理学院,广东 广州 510640)
0 引言
卖空交易机制对整个金融市场发展与完善起着至关重要的作用,已被应用到证券市场中[1]。在现实生活中,上市公司财务信息对股价变化产生了重要影响。投资者在选股时通常不是单纯地看股价,而是更多地关注上市公司的财务状况。若上市公司面临财务困境,则其股价将会暴跌,这将直接损害投资者利益。此外,在实际投资过程中投资者不仅面临金融市场风险,还面临由劳动收入、健康状况、利率等因素引起的背景风险[2]。可见,研究考虑卖空限制与财务困境的背景风险投资组合问题具有重要的现实意义。
依据背景风险对财富的作用方式,它可划分加性背景风险和乘性背景风险[3]。其中,加性背景风险[4,5]是附加于财富以外的风险,乘性背景风险[6,7]则是部分或完全作用于财富的风险。有关两类背景风险的研究已经取得了一定的研究成果。比如,Tsetlin和Winkler[2]提出了具有加性和乘性背景风险的最优风险选择模型;Franke等[8]分析加性和乘性背景风险对最优投资组合选择的影响;张尧等[9]研究具有加性和乘性背景风险的项目投资决策问题。另外,还有不少学者研究了卖空机制对投资决策的影响问题。徐晓宁等[1]研究了允许卖空条件下证券投资组合的区间二次规划问题。陈其安[10]分析考虑投资者情绪与允许买空卖空交易的投资组合问题。Kim等[11]提出考虑保守卖空机制的均值-方差投资组合选择模型。此外,上市公司的财务信息对股价及投资者投资意愿的影响不容忽视。王冀宁等[12]认为若上市公司业绩连年下滑将会削弱投资者的投资意愿。
综上所述,卖空机制、财务困境及两类背景风险对投资决策产生了深远影响。然而,现有的相关研究尚未同时涉及到以上三种因素。为此,本文考虑两类背景风险、保守卖空及财务困境的投资组合问题。相比于现有研究,主要贡献如下:所构建的模型同时考虑金融风险和非金融风险(背景风险)对投资决策的影响,这使得模型更加贴近实际。其次,引入保守卖空有利于投资者找到收益更高的投资策略,同时也降低了卖空下风险敞口对估计误差的影响。最后,考虑财务困境因素有助于投资者规避因财务困境导致损失,进而获得更为有效的投资策略。
1 模型构建
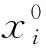
于是,投资于国外第k种金融资产折算成本币的资产收益率可表示为
(1)
由于乘积项rkry2是无穷小量,式(1)可近似表示为
(2)

于是,由加性背景资产和上述n种金融资产组成的资产组合净收益率可表述为:
(3)
类似于Kim等[11],我们假定投资者可对这n-2种风险资产进行保守卖空。记l≤0和h≥0分别表示风险资产k的投资比例xk的下界和上界。那么,风险资产k的投资比例可表示为:
(4)

(5)
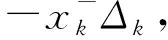
(6)
由式(3),可得投资组合收益率R的方差可表示为:

(7)
类似于Bell等[13],我们利用Z″评分法来度量各证券发行主体的财务困境。记S1,k、S2,k、S3,k和S4,k分别为风险资产k的证券发行主体的营运资本/总资产、留存收益/总资产、息税前利润/总资产、权益账面价值/总负债指标。于是,风险资产k的证券发行主体的财务困境得分Zk″可表示为
Zk″=6.56S1,k+3.26S2,k+6.72S3,k+1.05S4,k,k=3,4,…,n
(8)
其中,Zk″<1.81表示证券发行主体已经潜在破产,1.81
(9)
基于上述分析,假定在资产组合净收益率大于给定预期水平r的前提下,投资者寻求使得资产组合收益最大、资产组合风险最小及风险资产组合发行主体的财务困境最小的最优投资策略。于是,我们构建了如下考虑保守卖空和财务困境的背景风险投资组合模型(P):

2 带精英策略的非支配排序遗传算法
由于模型(P)是多目标规划问题,本文利用NSGA-II[14]来求解其Pareto最优解,算法具体步骤如下:

(10)
步骤2(适应度) 首先,借助罚函数法将约束条件l≤xi≤h和μR≥r整合到目标函数,将原问题转化为无约束优化问题。记M为惩罚因子,Xmax为个体前n个位置分量的最大值,Xmin为粒子前n个位置分量的最小值。于是,带有惩罚因子的适应度函数f1、f2、f3分别表示为:
f1=-μR+M[max{Xmax-h,0}-min{Xmin+l,0}-min{μR-r,0}]
(11)
(12)
f3=-ZP+M[max{Xmax-h,0}-min{Xmin+l,0}-min{μR-r,0}]
(13)
步骤3(非支配排序和拥挤度) 根据个体的适应度计算其非支配排序和拥挤度。进而,根据非支配等级对个体进行分层,记Li,m为同一层中个体i的第m个目标的拥挤度,具体计算方式如下:i)初始化所有个体的拥挤度为零;ii)每一层的I个个体按第m个目标函数值升序排列,排序边缘的个体设置拥挤度为无穷大,即L0,m=L1,m=∞;iii)排在中间的个体的第m个目标的拥挤度计算如下:
(14)
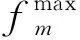
步骤4(选择操作) 根据排序结果及拥挤度大小,执行锦标赛选择操作。
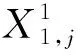
(15)
(16)

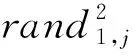
(17)
(18)

步骤7(合并种群) 合并父代和子代种群,并进行非支配排序和拥挤度计算。选择排序等级较低的进入下一次迭代,若排序等级相同,则选择拥挤度较大的个体。共选择pop个个体组成新的种群。
步骤8(终止条件) 若迭代次数达到最大迭代次数genmax,则输出结果,算法结束;否则,返回步骤4。
3 实证研究
3.1 数据选择和参数设定

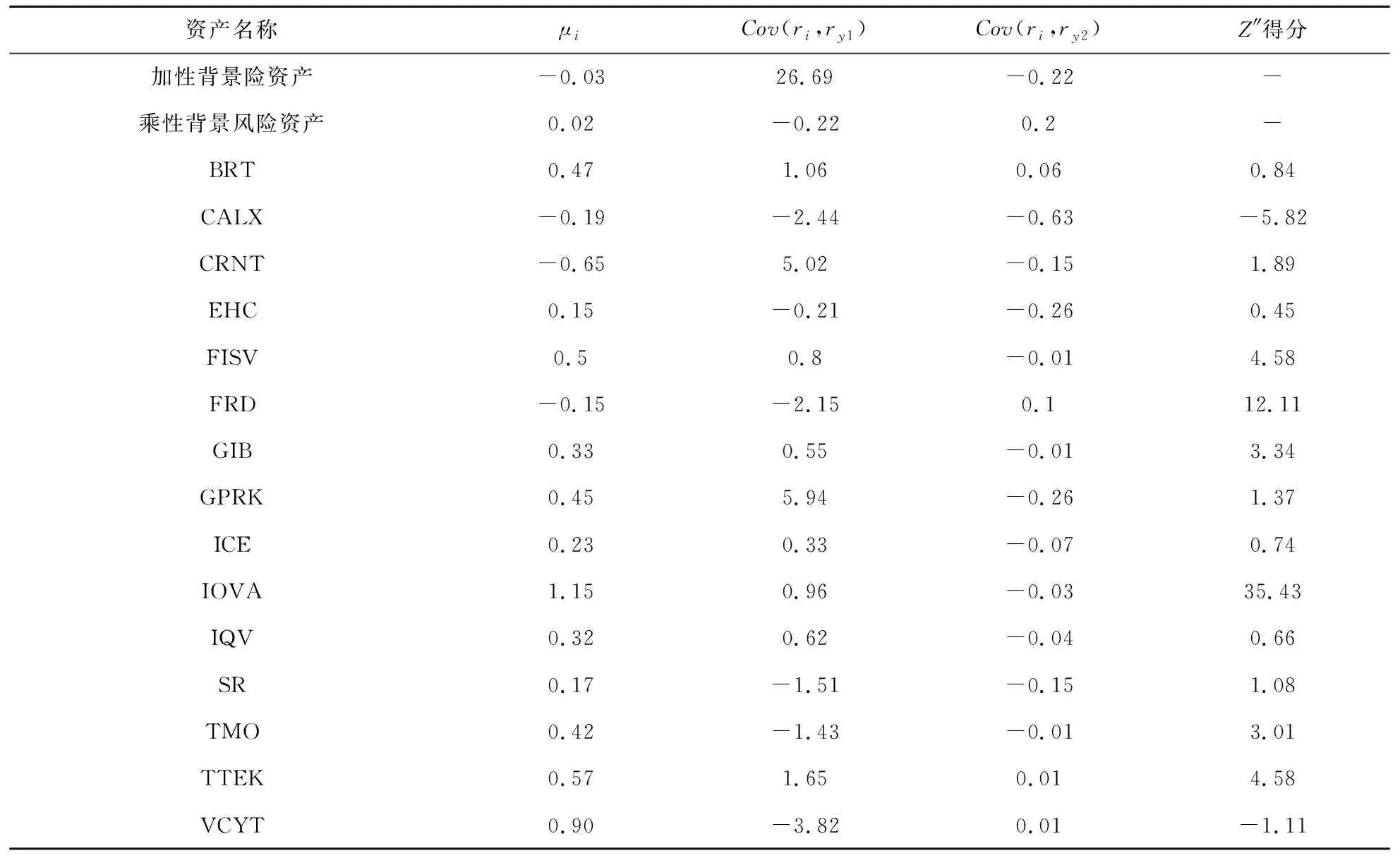
表1 相关统计指标及财务困境预测结果

表2 股票收益率的协方差矩阵
假定加性背景资产的投资比例为0.5,即ω=0.5;每只股票投资比例的上、下界分别为1和-1,即l=-1和h=1,空头头寸超出的水平为0.2,即γ=0.2。假定投资者对资产组合净收益率最低要求水平为0.0035,即r=0.0035。对于上述问题,利用本文所设计的NSGA-II算法求解对模型进行求解。算法参数设定如下:种群规模pop=500,最大迭代次数genmax=500,交叉概率Pc=0.9,变异概率Pm=0.1,交叉参数uc=1,变异参数um=20,惩罚因子M=105。
3.2 实证结果

由图2可知,当给定ZP″时,有效前沿表现为风险越大,收益越大,这与传统的均值-方差模型的有效前沿一致。由图3可知,在一定的μR下,ZP″越大则资产组合风险也越大。这是因为财务困境程度越小,表明财务困境程度低的资产的投资头寸较大,这使得资产组合分散化程度降低,进而导致资产组合风险增大。由图4可知,在一定的σR水平下,资产组合财务困境程度越大,则其预期收益也随之变大。
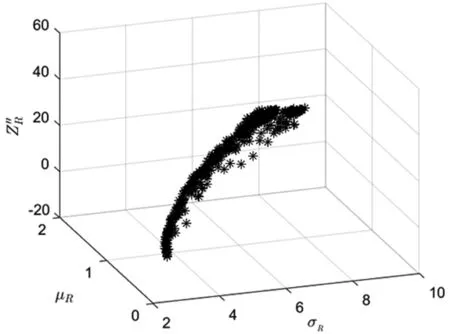
图1 关于(σR,μR,ZP″)有效前沿面

图3 当μR=0.35时(σR,ZP″)有效前沿
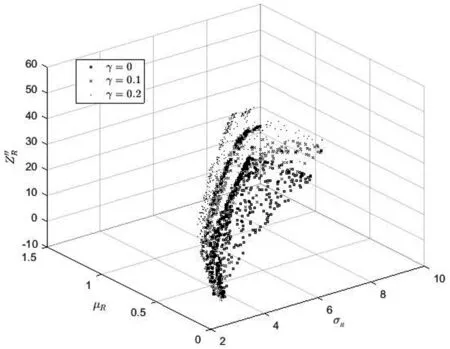
图5 不同γ水平下有效前沿面
3.3 参数分析

由图5可知,不同的保守卖空γ水平导致了不同的有效前沿面,这表明卖空保守程度影响了投资者的投资策略。由图6不难发现,随着γ的增大,(σR,μR)有效前沿将向上方移动,这表明γ增大有利于投资者获得更大的收益。图7刻画了给定在资产组合期望收益μR=0.35情形下,不同γ下(σR,ZP″)的有效前沿。由图7可见,在给定的风险水平下,随着γ的增大,资产组合的ZP″值越大;当资产组合ZP″值一定的情况下,资产组合风险将随着γ的减少而增大。由图8可见,当σR给定的情形下 (μR,ZP″)有效前沿随着γ的增大向右边移动,相应的资产组合收益也随之增大。这表明在资产组合风险一定的情况下,γ越大将有利于投资者获得更大的投资组合收益。
接下来,我们以γ=0.2为例分别分析加性背景风险和乘性背景风险变化对投资决策的影响。在这里,我们将加性背景资产的标准差变化α倍。不妨将α分别设置为0.5,1和2。通过对这三种情形进行计算得出结果见图9所示。为了分析乘性背景风险变化对投资策略的影响,我们不妨假定ZP″=20,进而将ry2的标准差和均值分别变动β倍和ε倍。在这里,我们讨论了(β,∈)=(0,0),(2,0)和(2,3)三种情况,通过计算得出的相应均值-方差有效前沿如图10所示。
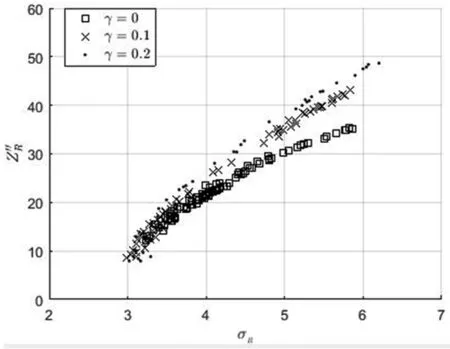
图7 当μR=0.35时不同γ下(σR,ZP″)有效前沿
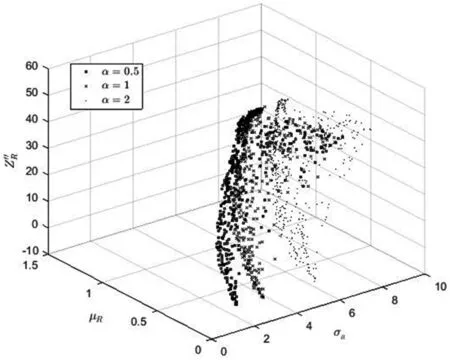
图9 不同α下有效前沿面
由图9可知,随着α的变化有效前沿面将随之变化。这表明当加性和乘性两种背景风险共同存在时,若投资者面临的加性背景风险增大,则投资者将获得更少的投资收益,同时资产组合的财务困境程度也将随之增加。综上可知,加性背景风险对投资有显著负面影响。由图10可见,不同乘性背景风险参数设置导致了不同的投资组合策略,这说明乘性背景风险影响投资决策。
4 结论
针对具有加性和乘两类背景风险的投资组合问题,本文考虑证券发行主体的财务困境因素、资产保守卖空限制及投资收益要求约束等现实市场限制,构建具有保守卖空和财务困境的背景风险投资组合模型。进而,利用NSGA-II算法对模型进行求解。最后,借助实证分析阐述了所构建模型的实用性。研究结果表明:卖空保守程度对投资有影响,保守卖空为投资者提供收益更大的可行投资策略。加性背景风险和乘性背景风险均对投资产生影响,两类背景风险变化均导致投资有效前沿面发生移动。由于保守卖空和两类背景风险对投资产生影响,并且考虑证券发行主体的财务状况能够更加客观地反映投资者的现实行为,故在投资组合问题中考虑卖空、财务状况和背景风险是实际而且重要的。

