基于改进型GERT网络的供应链突发事件风险传递研究

景 熠, 曹 柳, 张闻秋

(重庆理工大学 管理学院,重庆 400054)

0 引言

随着经济全球化进程不断加快和社会分工进一步细化，供应链成员企业的数量越来越多，相互依存关系日益紧密，其地域分布也更加广泛。供应链网络上任何一个成员企业遭受突发事件的冲击，其影响都会很快传递到与之相连的上下游合作企业，进而扩散到整个网络，严重时甚至会引起整个供应链运作进程的中断。例如，2014年由于美国高通公司受到“反垄断”制裁和英伟达公司决定退出手机芯片市场，造成小米手机连续超过五个月处于严重实质性缺货状态；2016年由于日本爱知钢铁工厂爆炸，迫使丰田汽车全面停产三周，本田和日产等其他汽车企业也中断了部分生产线。

目前，对供应链突发事件风险的研究，主要集中在供应链脆弱性评价[1,2]、突发事件风险因素[3～5]、响应策略[6,7]等方面。同时，由于突发事件对供应链局部节点的冲击会形成连锁反应，传递至整个网络，并且间接影响往往比直接影响更为剧烈，供应链突发事件的风险传递问题也越来越受到关注。

Bueno-Solana等[8]针对一个全球性供应链网络，基于系统动力学建模理论，以各级库存量和需求短缺量作为测量指标，分析了恐怖袭击引起的供应链风险扩散对运作绩效的影响。刘纯霞等[9]引入小世界网络模型分析了供应链中断风险传导路径对风险传导速度、传导广度和传导稳定三方面的影响。唐亮等[10]对关联供应链的无向信息层和有向物理层网络进行了结构分析，并研究了突发事件引起的网络级联失效传递机理。魏海蕊和盛昭瀚[11]考虑了供应链各节点之间的依赖关系，以不可运作性和经济损失为指标，对突发事件导致的扰动连锁传播而形成的间接影响进行了量化。曹岩等[12]利用图论和设计结构矩阵对供应链网络进行描述，并通过聚类分析，预测系统中突发事件的扩散路径和影响范围。Chen等[13]在强连接和弱连接视角下，运用无标度网络模型分析了供应链中断风险的传到通道与密度、传导鲁棒性、传导路径、传导范围等方面的特性。付焯等[14]针对企业供给间断和需求下滑引发的系统风险，以多式联运网络为研究对象，基于离散时间马尔科夫链构建了风险传导扩散模型，从风险传递速度、网络组织受染阈值等多个方面进行了深入分析。

图示评审技术(Graphical Evaluation and Review Technique，简称GERT)是在外部随机变化环境和系统内部随机因素共同作用下对系统的一种描述方法，为分析和解构复杂网络系统提供了有效工具[15]。王瑛等[16]根据复杂装备系统的风险特点，基于机会理论构建了不确定随机GERT网络模型，对不同类型的风险设计了对应的描述方法。郭本海等[17]构建了基于价值流动的乳制品全产业链质量管控GERT网络模型，分析了核心企业主导对于整个产业链质量管控的作用。王欢等[18]针对复杂产品质量价值的形成机理，构建了质量价值GERT网络模型，并提出了复杂产品供应链质量成本优化方法。

由多主体参与的多阶段、多环节供应链运作过程，具有网络化协作特点，并且在遭受突发事件冲击后，各个环节的运作将出现较大的不确定性，契合GERT网络的应用场景。因此，本文将GERT网络引入到供应链突发事件风险传递问题的研究中，针对问题特性，构建模型组，并设计相应的分析策略，对供应链突发事件风险传递进行定量化描述。

1 GERT网络模型构建

在供应链网络中，上下游节点企业(原材料供应商、制造商和分销商等)之间存在物料(原材料、零部件和产品等)的交付关系。如果供应链运作正常，各个环节的物料交付时间将在合理范围内波动，并不会产生明显的运作风险。然而，当某一节点企业遭受突发事件冲击后，通常会出现明显的运作中断，导致对下游企业的交付延迟。如果进一步衍生出次生事件或者节点企业应对不当，延迟情况可能会进一步加剧，并不断向下游叠加传递，进而造成巨大的断供风险，因此，为了定量化描述供应链突发事件的风险传递过程，本文首先运用随机网络理论，依次建立供应链正常交付模型、延迟交付模型和突发事件风险传递模型。

1.1 基于GERT网络的供应链正常交付模型

供应链正常交付模型的基本构成单元如图1所示，由节点、箭线和流三要素组成。节点i表示上游企业，节点j表示相邻的下游企业；箭线(i,j)表示节点企业i对节点企业j的物料交付活动；pT.ij表示正常情况下节点企业i对节点企业j完成物料交付的概率，tij表示节点企业i对节点企业j完成物料交付所需的时间。如果GERT网络完全由此类单元构成，即为供应链正常交付模型。

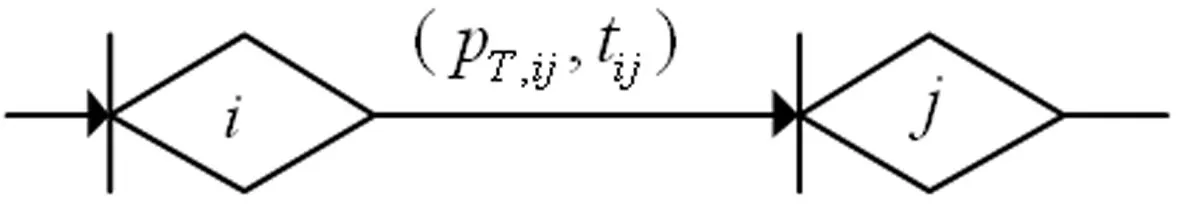
图1 供应链正常交付模型的基本构成单元

假设从节点企业i到节点企业j完成物料交付活动(i,j)的概率密度函数为fT(tij)，则随机变量tij的矩母函数可以表示为

(1)

其中，s为任意实数。此时，物料交付活动(i,j)的传递函数为

WT,ij(s)=pT,ij·MT,ij(s)

(2)

1.2 基于GERT网络的供应链延期交付模型

供应链延期交付模型的基本构成单元如图2所示。节点表示直接遭受突发事件冲击的上游企业，sti表示风险源点企业i遭受突发事件直接导致的交付延迟或中断时间；pLT,ij表示延迟情况下风险源点企业i对节点企业j完成物料交付的概率，pLT,ii表示风险源点企业i自身应对不当或次生事件导致延迟加剧的概率，pLT,jj表示节点企业j应对不当导致延迟叠加的概率。其他符号含义与1.1节相同。在供应链延期交付模型中，遭受突发事件冲击和影响的节点企业由此类单元表示。

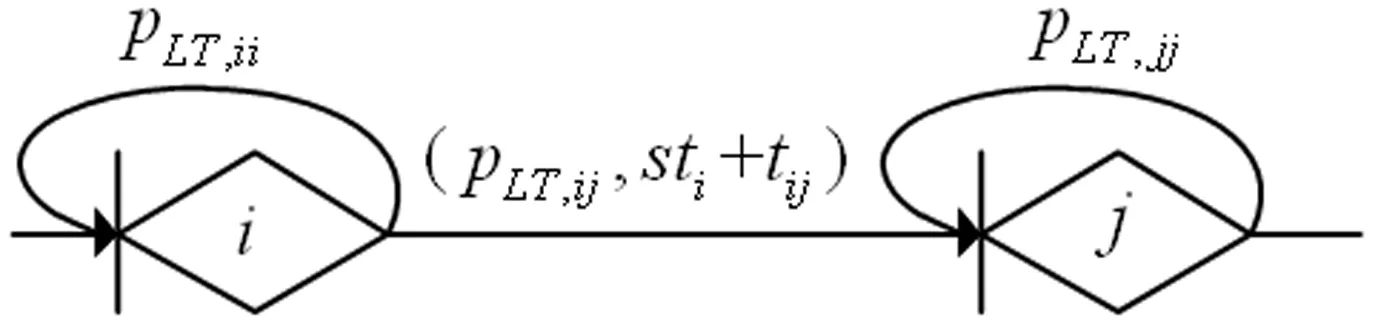
图2 供应链延期交付模型的基本构成单元

假设sti为常数，随机变量ltij=tij+sti的概率密度函数为fLT(ltij)，则相应的矩母函数可以表示为

(3)

此时，物料延期交付活动(i,j)的传递函数为

WLT,ij(s)=PLT,ij·MLT,ij

(4)

1.3 基于GERT网络的供应链突发事件风险传递模型

供应链突发事件风险传递模型的基本构成单元如图3所示。节点i表示直接遭受突发事件冲击的上游企业，节点i和k表示下游沿线企业；箭线(i,j)和(j,k)表示节点企业之间的风险传递过程；pR,ij表示风险源点企业i对节点企业j的风险传递强度，pR,jk表示节点企业j对节点企业k的风险传递强度；rj,ij，rk,ij,…,rn,ij,表示在(i,j)环节风险源点企业i向下游沿线各个节点企业j,k,…,n传递的风险量；rk,jk,…,rn,jk表示在(i,j)环节节点企业j向下游沿线各个节点企业k,…,n传递的风险量。随着交付时间不断延迟，供应链节点企业面临的风险也会不断加剧。因此，风险量rk,ij，rk,ij,…，rn,ij可以视为(i,j)环节最终延迟时间Δtij的函数，即rj,ij=rj(Δtij),rk,ij=rk(Δtij),…,rn,ij=rn(Δtij)。

图3 突发事件风险传递模型的基本构成单元

假设随机变量rj,ij和Δtij的概率密度函数分别为fR(rj,ij)和fΔT(Δtij)，则相应的矩母函数可以表示为

(5)

其中，h(rj,ij)为rj(Δtij)的反函数。

证毕。

此时，风险由节点企业i传递至节点企业j的传递函数为

WR,j,ij(s)=pR,ij·MR,j,ij(s)

(6)

2 模型求解

基于信号流图理论，依据梅森公式和矩母函数的基本性质，对上述模型进行数值解析。以供应链正常交付模型为例，从节点企业x到下游任意关联节点企业y逐级交付的等价传递函数为

(7)

从节点企业x到任意节点企业y逐级交付的等价传递概率和等价矩母函数分别为

pT,xy=WT,xy(o)

(8)

(9)

进一步，节点企业x到任意节点企业y逐级交付的期望时间及其分布方差分别为

(10)

(11)

供应链延期交付模型与突发事件风险传递模型的数值解析过程与上述过程基本相似。特别的，在突发事件风险传递模型中，风险由节点企业x传递至下游任意关联节点企业y、并以其为风险量化对象的等价传递函数为

(12)

其中，WR,y,d(s)表示以节点企业y为风险量化对象，由节点企业x到节点企业y的第d条直达路径的等价传递函数；WR,y,g(Lm)表示以节点企业y为风险量化对象，m阶环中第g个环的等价传递函数。

3 分析策略

通过对比供应链正常交付模型和延期交付模型的求解结果，可以得到各个环节的最终延迟时间；基于此，通过突发事件风险传递模型的拟合计算，进一步定量化描述风险在逐级传递过程中的扩大程度。具体分析步骤如下：

(1)分析目标供应链的结构特征和上下游物料交付关系，并通过历史数据，得到pT,ij交付完成概率，拟合正常交付时间tij的概率密度函数fT(tij)，从而构建基于GERT网络的供应链正常交付模型。

(2)计算正常情况下各环节交付活动(i,j)的矩母函数MT,ij(s)和传递函数WT,ij(s)，并在此基础上，计算期望时间ET(tij)。

(3)根据突发事件的性质和严重程度，预估受直接冲击企业的运作中断时间sti，并保留下游沿线节点企业及其箭线活动。依据节点企业自身实际和历史数据，预估各项概率数据，从而构建基于GERT网络的供应链延期交付模型。

(4)计算延期情况下各个环节交付活动(i,j)的矩母函数MLT,ij(s)和传递函数WLT,ij(s)，并在此基础上，计算期望时间ELT(ltij)。

(5)计算各环节的最终延迟时间Δtij=ELT(ltij)-ET(tij)。如果Δtij>0，说明物料交付活动(i,j)已经出现明显的延迟情况；如果Δtij=0，则说明物料交付活动(i,j)没有遭受断供风险。

(6)根据节点企业的实际情况，拟合风险函数rj(Δtij),rk(Δtij)，…，rn(Δtij)，从而构建基于GERT网络的供应链突发事件风险传递模型。

(7)计算风险传递过程(i,j)的矩母函数MR,j,ij(s),MR,k,ij(s),…,MR,n,ij(s)，以及传递函数WR,j,ij(s),WR,k,ij(s),…,WR,n,ij(s)。在此基础上，计算从风险源点企业i向下游沿线各个节点企业j,k,…,n传递的累加期望风险量ER(ri→j)，ER(ri→k)，ER(ri→n),以及分布方差VR(ri→j),VR(ri→k),…,VR(ri→n)。

4 案例分析

本文选取某汽车供应链网络为案例分析对象。该供应链网络由4个二级供应商、3个一级供应商、2个主制造商、3个经销商和5个零售商组成。依据结构特征和上下游物料交付关系，构建供应链正常交付模型，网络关系如图4所示，各个交付活动的相关参数如表1所示。依据式(1)和式(2)，可以得到各个交付活动的矩母函数MT,ij(s)和传递函数WT,ij(s)，如表2所示。

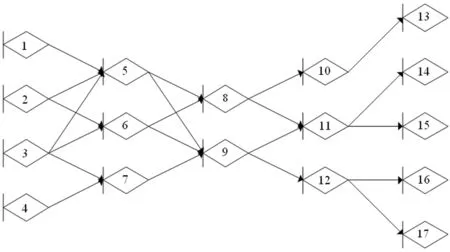
图4 基于GERT网络的供应链正常交付模型

表1 供应链正常交付模型各环节活动参数

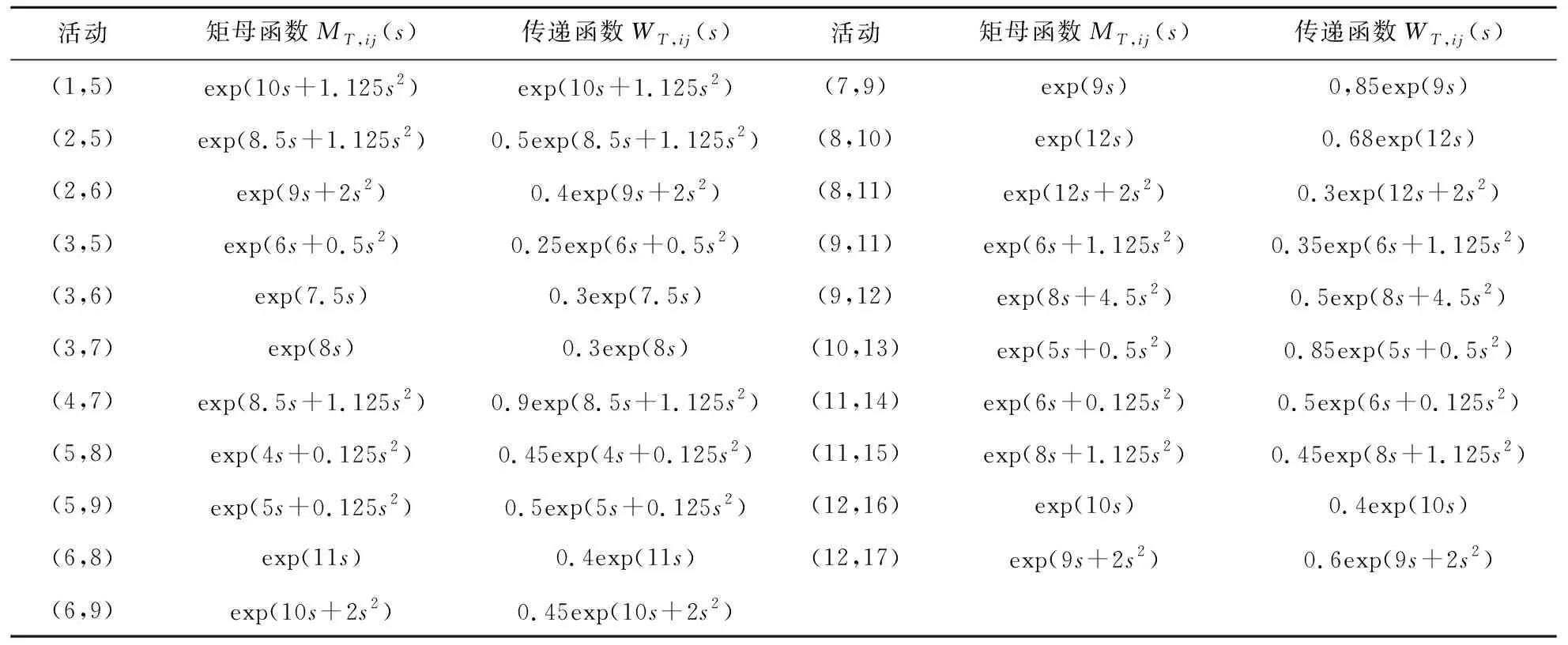
表2 供应链正常交付模型各环节矩母函数与传递函数

假设节点企业5直接遭受突发事件冲击，预计直接中断时间st5=21，下游沿线节点企业均有可能受到影响，形成自环结构，由此得到供应链延期交付模型，网络关系如图5所示，自环活动参数如表3所示，各环节的延期交付概率如表4所示。

图5 基于GERT网络的供应链延期交付模型

表3 供应链延期交付模型自环活动参数

表4 各个环节的延期交付概率

表5 各个环节的最终延迟时间

从表5可以看出，当节点企业5直接遭受突发事件冲击后，延迟时间不仅会依次向下游传递，并且下游沿线各个节点企业在各自的交付环节中还会产生新的延迟。进一步，基于各个环节的最终延迟时间，构建供应链突发事件风险传递模型，网络关系与图5类似，各个节点企业的风险量与最终延迟时间的函数关系如表6所示。

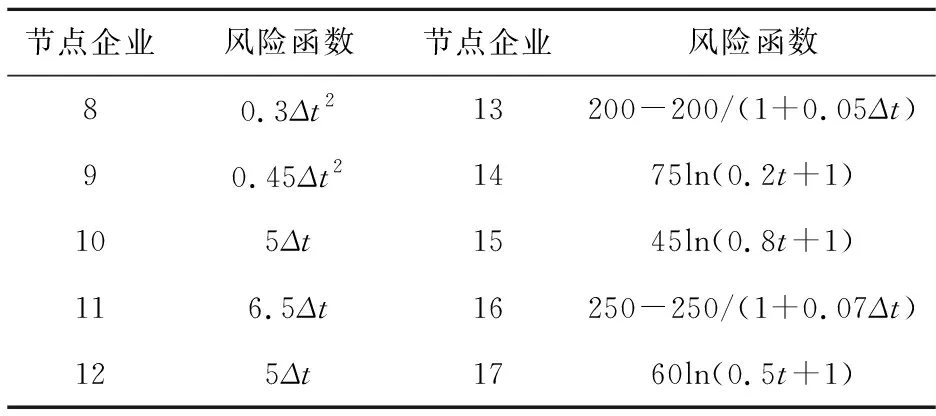
表6 各个节点企业的风险函数

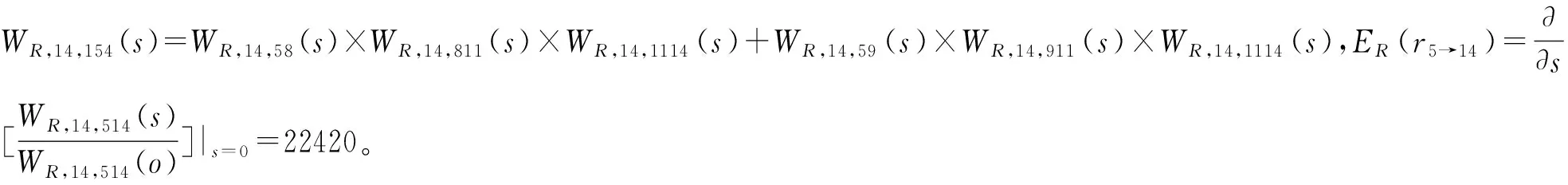
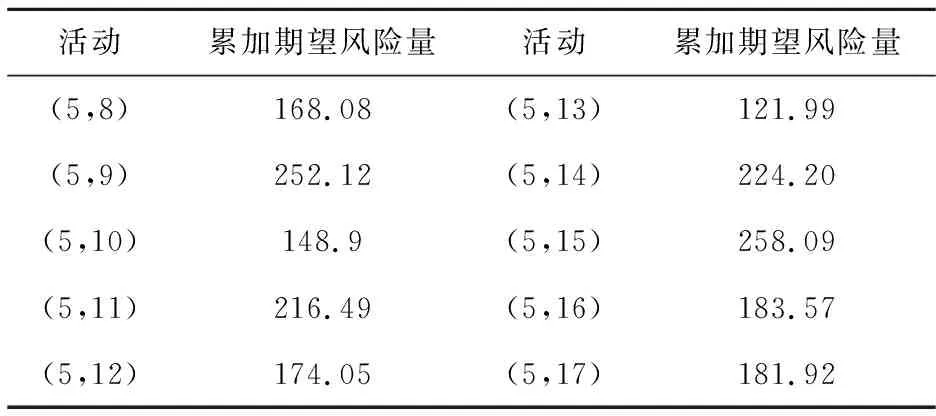
表7 各个节点企业遭受的累加期望风险量

从表7可以看出，在主制造商中，由于节点企业9对延迟时间的敏感程度较高，可能遭受的风险量较大；在经销商中，由于节点企业11同时受到两个主制造商的影响，可能遭受的风险量较大；在零售商中，节点企业15在经过多阶段较严重的延迟叠加之后，可能遭受的风险量较大。一旦供应链网络遭受突发事件冲击，这些企业均需要在风险管控中重点关注。

5 结束语

本文针对供应链突发事件的风险传递问题，分别构建了基于GERT网络的供应链正常交付模型、延期交付模型和突发事件风险传递模型，并推导了相应的矩母函数和传递函数表达式。在模型解析的基础上，设计了供应链突发事件风险传递的定量化分析策略。最后，通过一个简化的汽车供应链网络案例，验证了模型和分析策略的适用性。

本文主要研究了延迟交付风险从风险源点企业向下游沿线企业的传递过程，而没有考虑突发事件对上游沿线企业的影响。在实际运作中，上游企业可能会出现物料积压等风险。同时，对风险函数的分类和拟合分析，也需要更深入的研究。