“货到人”拣选系统中电商订单分批优化研究
李昆鹏, 刘腾博
(华中科技大学 管理学院,湖北 武汉 430074)
0 引言
近年来,随着电子商务的发展以及移动支付的普及,网络购物已经成为人们生活中不可或缺的一部分。数据显示,2019年“双十一”购物节天猫平台24小时成交额达2684亿元,订单量也从2009年的26万件增长到了12.92亿件,十年来增长4970倍,巨大的订单增长量对电商企业物流系统提出了更高的要求。据统计,在传统配送中心内部,拣选作业成本占总成本的60%,订单处理时间占比高达30%~40%。由此可见,订单拣选已成为制约电商发展的物流瓶颈。亚马逊在2012年斥资7.75亿美元收购Kiva Systems公司,其研发的Kiva系统可通过机器人搬运货架实现自动化拣选作业,该系统为其节省运营费用20%以上,且准确率高达99.99%,这也激发了我国大型电商企业开始积极研发仓储机器人(AGV)系统,并将其应用于订单拣选作业,实现“由人取货物”到“货物送到人”的转变。近两年,我国AGV技术发展迅速,面对不断趋于“多品种、小批量、高时效”的电商订单拣选挑战,如何对订单合理分批,更好地发挥AGV在拣选效率、作业准确率等方面的优势,已成为电商企业应用“货到人”系统进一步提升拣选效率的新途径。
在采用AGV的“货到人”拣选系统中,主要流程如图1中(a)所示。对于一定时间内的订单,首先根据商品需求和库存确定需要搬运的货架,并将搬运任务分配至AGV;然后AGV将货架运送至拣选站台,由拣选人员从货架上拣取商品并放入订单对应的周转箱;最后AGV再将货架运回原位,该模式可极大提高拣选效率。随着消费者需求不断趋于多样化,每个订单通常由多台AGV搬运多个货架才能满足,不仅浪费仓库资源,而且AGV数量的增加还导致发生碰撞的可能性增大。如果能建立订单与货架之间的联系,如图1中(b)所示,将调用货架相似度较高的订单合并为一个批次拣选,则AGV搬运货架一次可供应多个订单需求。订单合理分批不仅能够提高AGV工作效率,而且货架搬运次数的减少可有效缩短作业完成时间。基于此,本文以最小化AGV搬运货架次数为目标,深入研究“货到人”拣选系统的订单分批问题。该问题不仅要考虑订单的货架选取方法,还要设计批次划分标准,是一个十分复杂的NP-Hard问题,也是目前学术界和企业界关注较少但十分有必要优化的环节。
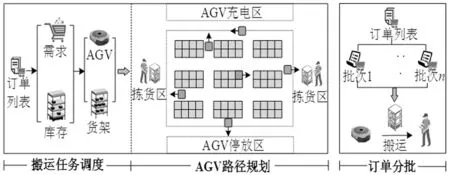
图1 “货到人”拣选系统流程
订单分批的概念早在1997年就由AcKerman[1]首次提出,目前在传统“人到货”拣选模式下关于订单分批问题的研究较多。在行走距离方面,郜振华等[2]、王转等[3]、Koch[4]等以拣选距离最短为目标,分别采用萤火虫分批算法、基于里程节约的方法、遗传算法求解。在拣选时间方面,Henn等[5]以最小化总延迟时间为目标提出变邻域搜索算法;王旭坪等[6]考虑订单平均服务时间最短构建模型;Lenoble等[7]和于岚等[8]以最小化订单完成时间为目标建立模型。在订单相似度上,李诗珍等[9]提出了基于储位、巷道及面积的相似系数计算方法;罗晓萌等[10]将通道重合数作为订单相似系数。Gademann等[11]通过复杂度分析证明了订单分批问题属于NP-Hard问题。
近年来,随着AGV技术的不断成熟,国内外学者对“货到人”拣选系统的订单分批问题开展了初步研究。范继东[12]以货架搬运次数最少为目标设计基于k-means聚类算法的订单分批算法;李珍萍等[13]以人工拣货成本和AGV搬运成本之和最小为目标建立模型。部分学者将订单分批问题与其他问题相结合进行探索。Xiang等[14]和李晓杰[15]结合储位分配问题,前者以最大化订单关联度和最小化货架访问次数为目标构建模型;后者以减少AGV往返运送货架次数为目标设计拣选策略。Boysen等[16]和吴颖颖等[17]考虑拣选顺序,前者优化目标为最小化AGV搬运货架次数;后者为最大化单拣选站台订单耦合因子之和。Ardjmand[18]研究了订单分配、订单批处理及拣选路径问题。
综上所述,国内外学者主要研究了传统“人到货”拣选模式下的订单分批问题,而采用AGV的“货到人”拣选系统与其具有本质区别,很多研究成果和算法不能直接应用。目前关于“货到人”拣选系统订单分批问题的研究较少,已有文献多在订单与货架对应关系已知的情况下构建数学模型并设计启发式算法求解,且多假设每种商品只能存储在一个货架上。而在实际中,电商订单信息通常包括所需商品及数量,且商品库存在多个货架上均有分布,应首先根据订单需求选取供应货架。鉴于此,本文在构造模型时考虑订单需求与商品库存之间的联系,在设计算法时定义货架相似度作为订单选取货架的评价指标,最终形成一套能够最大化减少AGV搬运货架次数的订单分批方案。
基于以上分析,本文考虑在订单需求多样化、商品库存多货架分布、订单与货架供需关系未知等更符合实际的背景下研究订单分批问题。首先,构建以最小化AGV搬运货架次数为目标的整数规划模型;然后,设计两阶段订单分批启发式算法,并提出两种方法创建新批次;最后通过实验验证本文模型和算法的有效性,分析两种批次创建方法的适用性,采用灵敏度分析探讨周转箱的合理配置数量。实验证明本文提出的两阶段算法能够在短时间内得到较优分批方案,在实际应用中具有一定的可行性。研究成果不仅可以扩展订单分批问题的现有理论,而且能够为企业采用AGV进一步提升拣选效率提供新的思路。
1 考虑货架搬运次数订单分批模型
1.1 问题描述及假设
本文研究“货到人”拣选系统的订单分批问题,描述如下:在采用AGV的智能仓库中有t个拣选站台、r个货架,共存储h种商品。每个货架有多个储位,每个储位存放一种商品,每种商品存放在多个货架上。每个拣选站台配备d个周转箱,每个周转箱对应一个订单。某段时间内共接收到n个需求已知的订单拣选任务,如何对这些订单进行分批以实现批次拣选作业。在“货到人”拣选系统中,作业完成时间主要取决于AGV搬运货架的行走时间,若能调用较少货架满足所有订单的商品需求,则可最大程度减少作业完成时间。基于此,本文以最小化AGV搬运货架次数为目标,决策多订单的批次分配及批次与货架的服务关系,并计算批次的商品需求量及货架的供应量。为方便建模,考虑以下假设:
①AGV电量充足,且数量足够多;②商品库存量充足能够满足订单集合需求;③在给定的时间段内每个货架只能被AGV搬运一次;④同一订单不能被分配至多个批次;⑤每个拣选站台完成一个批次的拣选作业,即批次数等于拣选站台数t,批次的最大订单数等于周转箱数d。
1.2 模型建立
根据问题描述,符号及变量定义如表1所示,数学模型构建如下:

表1 模型符号变量定义
(14)
目标函数(1)表示最小化AGV搬运货架次数;式(2)保证每个订单均被分配至批次;式(3)保证每个批次均会被货架服务;式(4)表示每个批次至少包含一个订单;式(5)为批次的最大订单数限制;式(6)表示每个货架最多服务一个批次;式(7)表示批次需求等于其所包含订单的商品需求量之和;式(8)表示批次需求可被多个货架供应;式(9)表示货架的供应量不能超过其存储量;式(10)保证批次的商品需求都能被满足;式(11)表示货架是否被搬运取决于其是否供应批次商品需求;式(12)表示0-1变量;式(13)、(14)表示整数变量。
2 基于货架相似度的两阶段订单分批算法
订单分批是将订单集合划分为包含一个或多个订单的批次进行拣选,本文提出了基于货架相似度的两阶段订单分批算法SSTOBA(Shelf Similarity based Two-phase Order Batching Algorithm),如图2所示。第一阶段,包括新批次创建和订单加入批次两个步骤:(1)采用两种方法创建新批次。法一:计算两两订单的货架相似度并将相似度最大的合并作为新批次,若最大相似度为0,则将订单各自作为拣选批次;法二:计算每个订单的所需货架数并将数值最大的作为新批次。(2)订单加入批次。计算订单与当前批次的货架相似度并将相似度最大的订单加入,直至订单数达到周转箱数,在此过程中若最大相似度为0,则将当前批次作为拣选批次。通过以上两个步骤将所有订单分配至批次。然后,遍历每个订单作为第一个初始批次得到各自分批方案,将较优方案作为初始解。第二阶段,设计局部搜索算法改进初始解,通过两种移除算子和修复算子不断更新当前解,得到最优解或近似最优解。

图2 求解框架
为建立订单与货架之间的供需匹配关系,在算法中考虑两种规则为订单选取货架,然后定义货架相似度函数作为评价指标。本节先对货架选取规则和相似度函数进行说明,在此基础上介绍算法两个阶段的具体步骤。
2.1 两种订单选取货架规则
电商订单所需商品通常来自多个货架,同种商品在多个货架存储,因此每个订单对应多种货架组合。在实际中订单与货架的匹配关系未知,需首先对货架量化作为选取依据。本文结合订单需求量和商品库存量的关系提出两种货架量化标准。其中,Om表示订单需求商品m的数量,Skm表示货架存储商品m的数量,具体描述如下。两种标准为货架存k储或可满足订单需求商品的类型数,分别表示为Mk和Nk。当订单对商品m有需求,若货架k存储商品m,即Om>0,Skm>0,则Mk值加一;若货架存储商品且库存量满足需求量,即Om>0,Skm>Dm,则Nk值加一,检测所有商品需求得到货架k的Mk值和Nk值。
为得到较优组合,在对货架量化基础上,提出两种货架选取规则,区别在于Mk和Nk的计算次序不同,如图3所示。对于货架集合S={1,…,r}。首先,根据订单需求Om,计算每个货架的Mk值(Nk值)并选择最大值货架。若存在h个货架具有最大值,则比较货架的Nk值(Mk值)并选择最大值货架。若仍存在t个货架两数值均最大,则从中随机选择货架。然后,使该货架尽可能满足订单需求,更新Om和Skm。最后,按照两种规则不断选择供应货架,直至订单的所有商品需求均被满足,由此得到订单的两种供应货架组合。
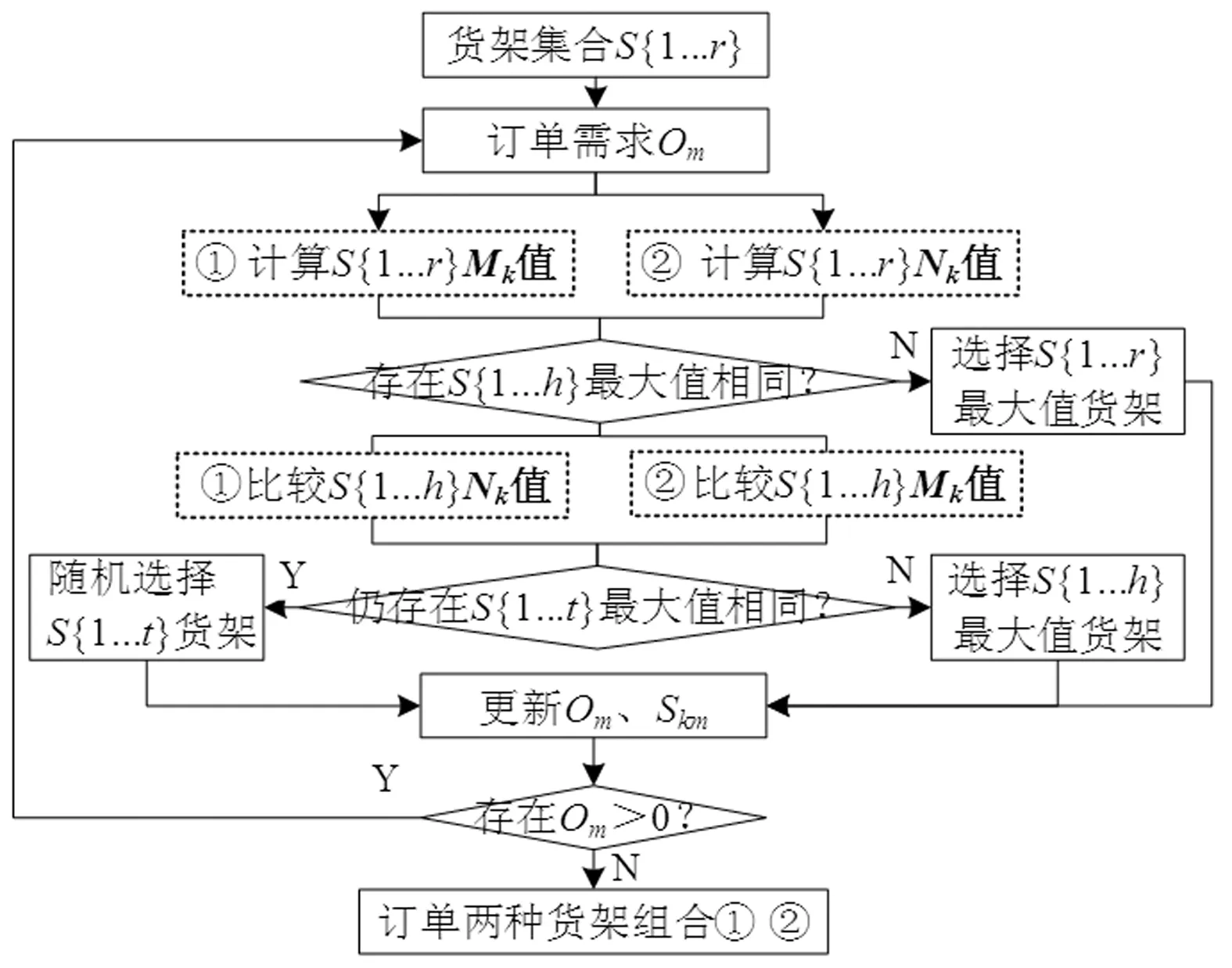
图3 两种货架选取规则
2.2 货架相似度函数
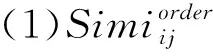
(15)

(16)
(17)
2.3 两阶段算法步骤
2.3.1 第一阶段生成初始解
本文算法基于订单选取货架规则和货架相似度函数,在第一阶段,根据批次中是否已有订单进行新批次创建及订单加入批次,提出两种方法创建新批次,①两订单货架相似度最大;②单订单所需货架数最多,分别表述为法一和法二。为扩大搜索空间,遍历订单集合,各订单依次作为第一个批次,得到基于每个订单的分批方案。由于订单在两种规则下选取货架对应两种货架组合,最终得到2n种分批方案。鉴于每个方案均建立在第一个批次已有订单的基础上,为更清楚展现算法逻辑,描述顺序为订单加入批次和新批次创建,主要流程如图4所示,具体步骤如下。
(1)订单加入批次

Step2若批次中订单数小于周转箱数,返回Step1,继续加入订单;若已达到周转箱数,则当前批次为拣选批次,删除其供应货架,执行Step3。
Step3若集合中订单数大于1,则生成新的空批次,执行Step4采用两种方法创建新批次;若订单数为1,则该订单为拣选批次,终止算法。
(2)新批次创建

Step4(法二) 当批次为空,按所需货架数对集合中订单排序,将所需货架数最多的订单作为新批次,并将其从集合中删除,返回Step1。
同理得到O={1,…,n}中每个订单的两种货架组合分别作为第一个批次的分批方案,共得到2n种订单分批方案,计算每个方案中AGV完成所有订单拣选任务的搬运货架次数,将搬运次数最少的作为第一阶段初始解s0。
2.3.2 第二阶段局部搜索算法改进初始解
基于第一阶段所得初始解,为提高算法寻优能力以获得高质量的解,在第二阶段加入局部搜索算法,包括破环与修复两个步骤,通过两种移除算子和修复算子改进当前解,主要步骤如下。
两种移除算子:①移除批次订单。在当前解中,随机选择20%的批次,从每个批次中随机移除一个订单,得到破坏解sd。将移除的订单存入未分批集合R,对应货架存入可用货架集合S;②移除订单货架。在当前解中,随机选择30%的货架移除,存入可用货架集合S,同时将对应订单删除,存入未分批集合R,得到破环解sd。
修复算子:基于货架集合S,对订单集合R,计算各订单与破坏解sd中所有未饱和批次的货架相似度(订单数未达到周转箱数),将相似度最大的订单插入,并将其从集合R中删除,同时将其所需货架从集合S中删除。继续执行插入,直到集合R中的订单均分配至批次,得到修复解se。
Step1参数初始化。输入第一阶段初始解s0,初始目标函数值为AGV搬运货架次数r0;初始化当前解rc和当前目标函数值sc,使sc=s0,rc=r0;设置l=0,L=0,当前解最大未改善次数lmax,算法最大迭代次数Lmax。
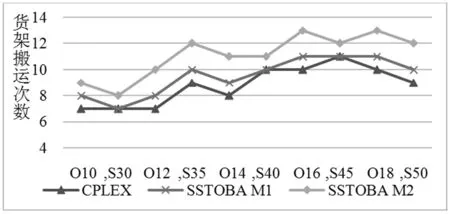
Step2若L Step3若l Step4通过移除算子得到破环解sd,然后采用修复算子得到修复解se。计算修复解se的货架搬运次数,作为其目标函数值re,如果re Step5输出近似最优解s*=sc,近似最优目标函数值r*=rc。 本文所有测试在Intel Core i5 2.2GHz CPU with 4GB RAM的计算机上运行,采用CPLEX作为模型求解器,启发式算法采用C++编码,实验部分设置最大迭代次数为100。 为验证本文数学模型和算法中两种批次创建方法的有效性,采用小规模算例对比分析CPLEX与算法求解结果。为使算法所得批次数等于拣选站台数,以不影响货架搬运次数为前提改进算法所得方案,在符合周转箱数范围内将包含订单数较少的批次合并。本文考虑订单需求多样化、商品库存多货架分布的特点随机生成数据,对5组不同规模的算例测试。其中,总商品类型数为8,拣选站台数为5,周转箱数为4。 结果如表2所示,以AGV搬运货架次数(Out)为衡量指标。M1、M2分别表示第一阶段新批次创建的法一和法二;CS1、CS2分别表示最优解与法一、法二求解所得百分差,等于“(SSTOBA-CPLEX)/SSTOBA*100%”;time1、time2、time3分别表示CPLEX、法一、法二的求解时间。 表2 小规模实验结果 图5 三种方式下货架搬运次数对比图 结果表明,(1)对于货架搬运次数,如图5所示,在不同算例规模下,CPLEX求解模型可最大程度减少搬运次数。在两阶段算法中,采用不同方法创建新批次对求解结果有所影响,法一比法二能够获得更少的搬运次数。此外,对于表现较好的法一,搬运次数与最优解仅相差1~2次,平均相差7.4%,且在有些情况下能够获得最优解,说明算法具有合理性和有效性。(2)在求解时间上,如图6所示,当订单数由14、货架数由40不断增加时,模型求解时间呈指数型增长,由于电商配送中心对时间要求极高,CPLEX在求解大规模问题时耗时较长,因此很有必要探索高效的启发式算法,而本文算法能够在短时间内获得AGV搬运货架次数较少的订单分批方案,具有很好的实用性。由此可见,本文建立的数学模型是正确且有效的,两阶段算法中的法一能在短时间内获得最优解或近似最优解。 为分析本文在第一阶段提出的两种批次创建方法的适用性,以及局部搜索算法对初始解的改进效果,本节采用两阶段算法对更大规模算例测试。在衡量分批效果上,选取AGV搬运货架次数(Out)和分批后的批次数(Batch)两个指标评价。实验结果如表3所示,其中,P1、P2分别表示第一阶段和第二阶段;P1O、P2O分别表示在第一阶段和第二阶段法一与法二在搬运次数上的差异,计算分别为“(P1 M1-P1 M2)/P1 M2*100%”和“(P2 M1-P2 M2)/P2 M2*100%”,负号表示相对减少;M1O、M2O表示法一和法二在两个阶段结果的百分差,计算分别为“(P1 M1-P2 M1)/P2 M1*100%”和“(P1 M2-P2 M2)/P2 M2*100%”;BGap表示法一与法二在批次数上的差异,等于“(M1-M2)/M2*100%”。 表3 大规模实验结果 由结果可知,(1)对于货架搬运次数,如图7所示,由P1O、P2O可知,法一与法二的搬运次数相差较大,在第一阶段法一比法二平均减少40.3%,在第二阶段平均减少38.5%;由M1O、M2O可知,采用局部搜索算法能在一定程度上改善初始解,与第一阶段相比,法一与法二分别平均节约搬运次数23.4%和32.4%。法二改进后的解仍比法一初始解的搬运次数多,主要原因是,在第一阶段,法一将货架相似度最大的两个订单合并作为新批次,更能节约搬运次数,初始解与近似最优解差距较小。(2)对于批次数,如图8所示,法一得到的批次数较多,由BGap可知法一比法二平均增加42.9%,最大差距为66.7%。主要原因是,法一考虑当不存在两订单所需货架相同时将订单各自作为拣选批次,故出现批次中仅包含一个订单的情况较多导致批次数增加。综上,采用法一的两阶段算法能够获得更少的搬运次数,从而有效缩短AGV搬运货架行走时间。 图7 两种方法不同阶段货架搬运次数差异图 图8 两种方法批次数差异图 在采用“货到人”拣选模式的仓库中,每个拣选站台配备一定数量周转箱,分别对应一个订单。周转箱作为物流容器,数量过多将会占用空间且增加采购成本,因此,本节基于两阶段算法探讨周转箱的合理配置数量。随机生成一组中等规模算例:总商品类型数为20、订单数为30、货架数为60。结果如表4所示,其中,time1、time2分别表示法一和法二的求解时间;P2O、BGap分别表示法一与法二在货架搬运次数、批次数上的差异,负号表示相对减少。计算分别为“(P2 M1-P2 M2)/P2 M2*100%”和“(M1- M2)/M2*100%”。 表4 周转箱数量灵敏度分析 由结果可知,随着周转箱数的增加,两种方法在货架搬运次数和批次数上基本呈现由下降到平稳波动的变化趋势,如图9和图10所示。主要原因是,订单加入批次的停止条件包括两个,订单与批次不存在所需货架相同以及批次订单数达到周转箱数。(1)当周转箱数较少时,即使存在订单与批次的所需货架相同,由于最大订单数限制可能无法继续加入批次。(2)当周转箱数由4增加至10时,批次可包含订单增多,将相似度最大的订单加入批次能有效减少搬运次数,同时,批次中订单数的增多导致总批次数减少。(3)当由10逐步增加时,批次最大订单数的限制作用不明显,订单停止加入批次主要是由于不存在所需货架相同,此时周转箱数的增加对搬运次数和批次数的影响很小。由此可知,在中等规模下合适的周转箱数为9~10个,此时货架搬运次数较少且周转箱利用率较高。综上,通过对周转箱数量进行灵敏度分析,可为不同仓库规模的周转箱数量配置提供参考,达到合理利用仓库资源、提高企业经济效益的目的。 图9 不同周转箱规模下货架搬运次数变化图 图10 不同周转箱规模下批次数变化图 本文研究了“货到人”拣选系统的电商订单分批问题,考虑订单需求多样化、商品库存多货架存储以及订单与货架匹配关系未知等实际因素,以最小化AGV搬运货架次数为目标构建数学模型,并设计基于货架相似度的订单分批算法求解。最后通过实验验证了本文模型和算法的有效性和实用性,实验结果表明,(1)采用法一基于两订单货架相似度最大的两阶段算法能获得更少的搬运次数,在有些情况下能够获得最优解。(2)本文算法能够在具有110个货架、28种商品的仓库中对55个订单分批处理,在第二阶段,法一和法二比初始解分别平均减少搬运次数23.4%和32.4%。(3)在中等仓库规模下周转箱合理配置数量为9~10个。综上,本研究不仅扩展了“货到人”拣选系统中订单分批问题的相关理论,而且可为企业通过订单分批进一步提高AGV拣选效率提供参考。此外,考虑多种实际因素对智能仓库建设具有重要理论价值和现实意义。未来的研究中,可以考虑将AGV路径规划与订单分批相结合进行深入探讨,此外,还会考虑在线订单分批问题。3 仿真实验及数据测试
3.1 小规模仿真实验

3.2 大规模仿真实验
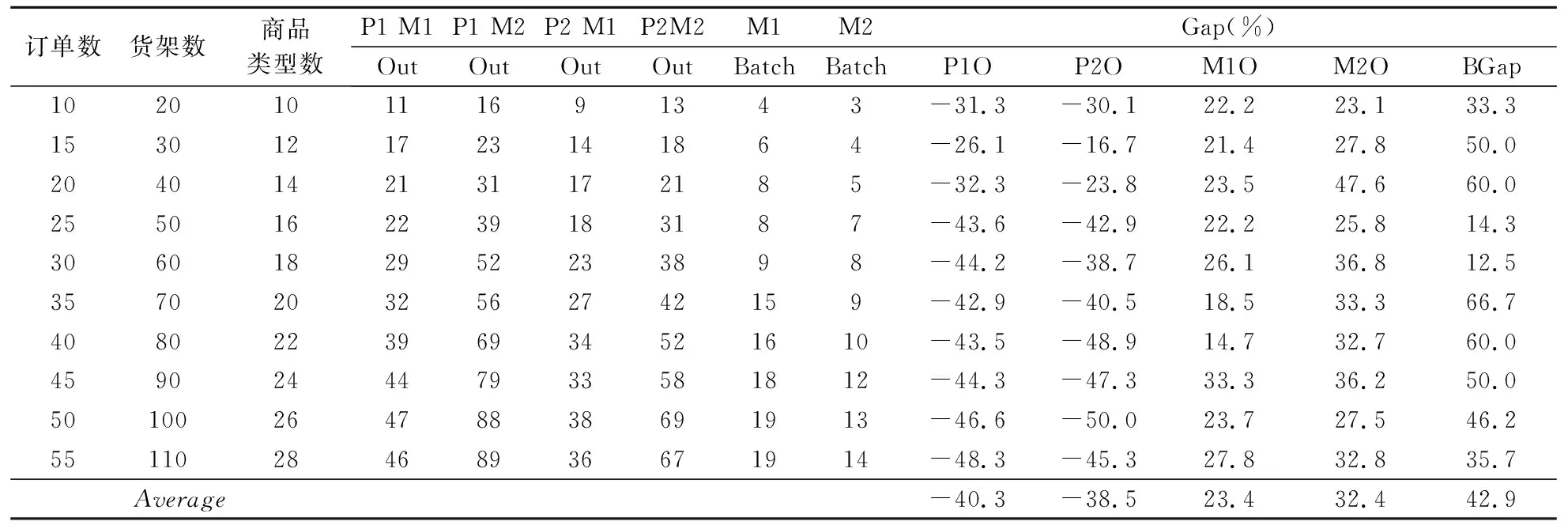
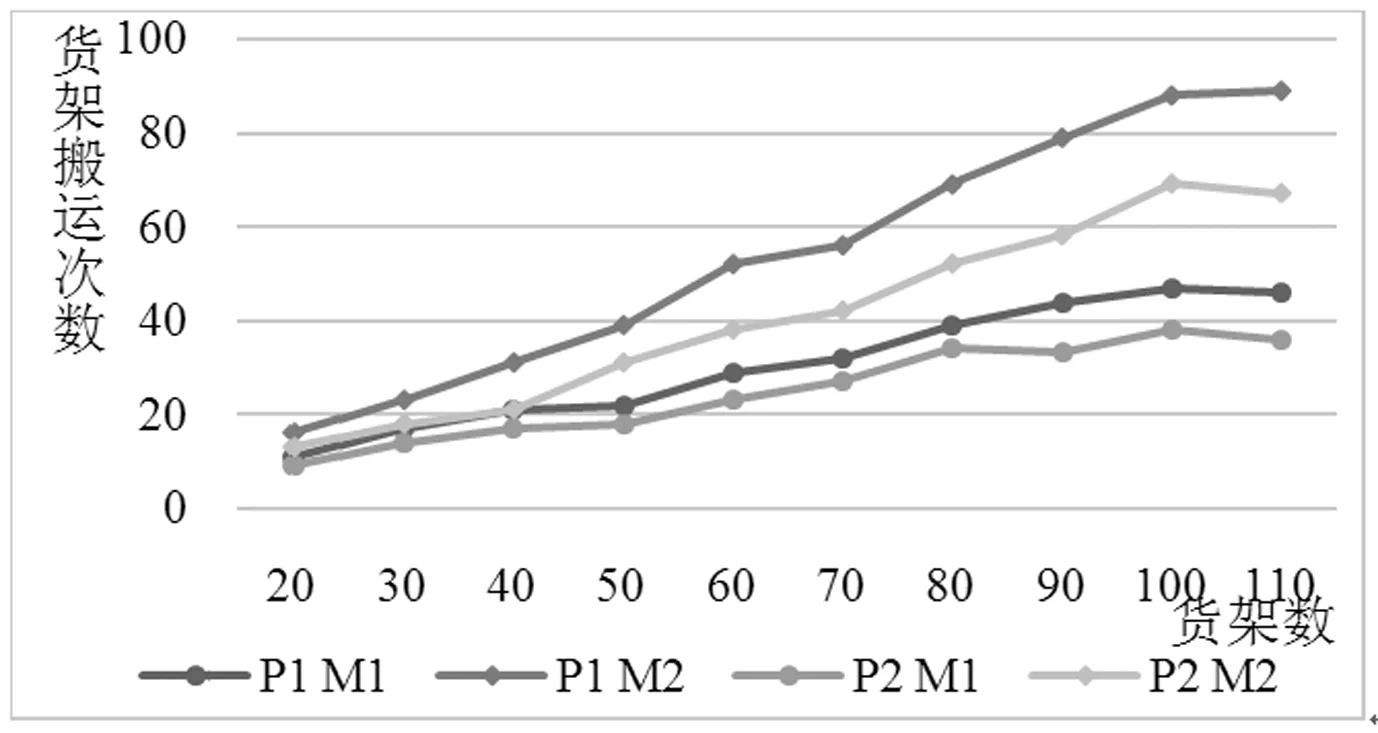

3.3 周转箱数量灵敏度分析

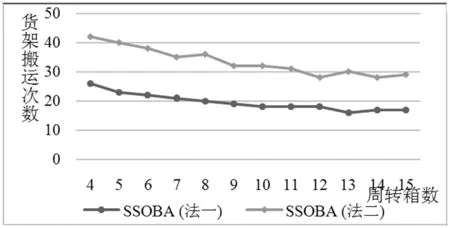
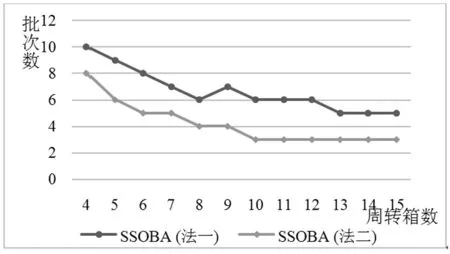
4 结论

