基于高光谱植被指数的水稻LAI遥感估算

张 敏, 郭 涛，刘 轲，黄 平，喻 君，刘仕川，刘泳伶,李源洪

(1. 四川省农业科学院遥感应用研究所/农业农村部遥感应用中心成都分中心，成都 610066；2.凉山彝族自治州昭觉县农业局，四川 昭觉 616150)

【研究意义】叶面积指数(Leaf area index, LAI)反映农作物对太阳光能的截取能力，是作物水肥调控、长势监测和产量评估的重要指标[1-2]。遥感技术以其经济、高效和无损的优势，已成为LAI估测(又称“反演”)的有效技术手段[3-4]。高光谱遥感利用众多窄而连续的通道获取光谱信息，能够更准确地反映植被特征[5-6]。因此，实现高效、准确的LAI高光谱遥感估算，对于现代农业的数字化、智能化生产和管理具有重要意义。【前人研究进展】基于统计模型的LAI高光谱遥感估算简便易行，中、小尺度上精度较高，应用较为广泛。然而，统计模型对于具体的环境和作物状况，大尺度上适用性较差[7]。因此，应针对具体的研究区域和目标作物，充分考虑LAI统计估算模型的影响因素，以提高模型的适用性。相关研究表明，以下三方面因素对基于统计模型的LAI高光谱估算具有重要影响。①表征LAI的特征参量。LAI特征参量即LAI统计估算模型的自变量。植被指数(Vegetation index, VI)能够突出植被特征，减少大气和土壤背景等因素的干扰，加之其计算便捷，因此，是最为常用的LAI特征参量[8-9]。现有研究通常采用前人推荐的波段(以下简称“默认波段”)计算高光谱VI[10-12]。然而，LAI的敏感波段往往因环境和植被类型而异[13]。为确保LAI估算精度，Xing等[14]首先选择LAI敏感波段，进而利用敏感波段计算VI；Peng等[15]和Wang等[16]利用任意波段组合计算VI，进而构建VI与LAI之间的关系矩阵，遴选令相关系数最大的波段组合。比较而言，后一种方法能更直观地反映VI与LAI之间的相关程度。②回归建模方法。参数回归常用于构建基于VI等一维变量的LAI统计估算模型[7]。以Verrelst等[9]为代表的一些研究认为，机器学习算法比常规的参数回归具有更好的鲁棒性和泛化能力，更适合于拟合高维度、非线性的统计关系。近十几年来，研究者尝试基于全波段或特征波段的冠层反射率或光谱导数等多维特征参量，利用机器算法开展LAI高光谱反演[7]。林卉等[11]和姚雄等[17]尝试结合VI与机器学习来估算LAI。 ③训练样本量。用于建模的训练样本量对基于统计回归模型，特别是基于机器学习的LAI反演精度与稳定性有显著影响[18-19]。然而，训练数据往往通过田间实测来获取，其过程费时费力，成本较高。因此，往往需要找到满足应用需求的适宜建模样本量[19]，或选择适于小样本的机器学习算法[19-21]。【本研究切入点】应针对具体的研究区域和目标作物，合理确定各影响因素，探索本地化的LAI高光谱遥感估算模型。本文以四川省凉山彝族自治州昭觉县水稻为例，基于不同样本量的3套训练样本，基于单一VI，利用指数回归(Exponential regression, ER)和人工神经网络(Artificial neural network, ANN)开展VI波段选择和LAI统计估测模型构建。【拟解决的关键问题】探索VI及其波段选择、回归建模方法和训练样本量对基于统计模型的LAI高光谱遥感估测的影响，研究适用于昭觉县水稻LAI遥感监测的模型和建模技术流程，为园区至县域尺度LAI遥感监测开展关键技术试验，积累研究经验。

1 材料与方法

1.1 材料获取

1.1.1 研究区域和田间测量 研究区域位于四川省凉山彝族自治州昭觉县地莫镇，地处102.772° ～ 102.787°E，27.865°～ 27.915°N(图1)。昭觉县地处凉山州中部东侧，为低纬度高海拔中山和山原。

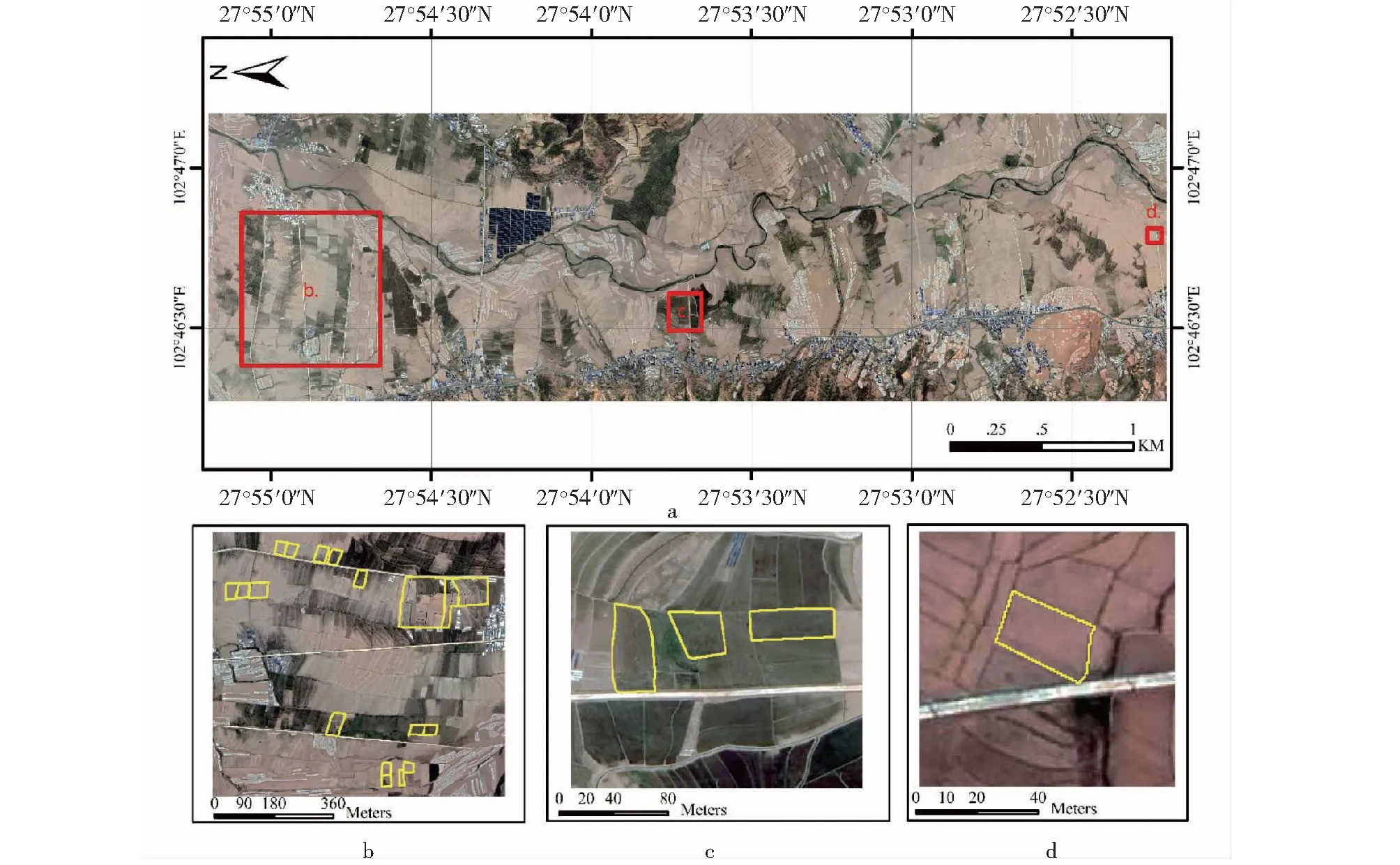
图1 样方分布Fig.1 Study sites

具有冬季干寒而漫长、夏季暖和湿润的高原气候特点，年平均气温10.9 ℃，常年平均日照 1865.5 h[22]，适宜开展遥感监测。

田间测量分别于2018年7月18—21日(拔节期)和8月14—18日(抽穗期)开展。在研究区域内选取22块稻田(图1)。在面积较小或内部LAI较均一的田块内随机布设2～3个样方；在面积较大且LAI分布较不均的田块内，按LAI的分布梯度布设4～6个样方。每个样方面积约为1 m(顺垄方向)× 4垄(垂直垄方向)，在其中开展测量。利用美国 ASD FieldSpec 4 光谱仪，采用视场角为25°的裸光纤，距冠层顶部高度约1 m，垂直向下测量其冠层反射率，每个样本点重复观测5次。农作物LAI的敏感波段多集中于可见光—近红外区间[7]。因此，为减少数据冗余，截取光谱范围为400～1220 nm，光谱分辨率重采样为5 nm。为减少可能的随机噪声，利用Savitzky-Golay(SG)滤波器对光谱数据滤波[23]。利用英国Delta T SunScan 冠层分析仪测量LAI。2次测量一共获取103个样本点。

1.1.2 样本划分 首先，按常规方法，随机选取103个样本点的70%(72个)作为训练样本，30%(31个)作为测试样本。为探索样本量对LAI估算精度的影响，从72个训练样本中再随机抽取24、48个样本点，形成样本量不同的3套训练样本。采用同样的31个测试样本点来验证所有试验的LAI估算精度，以确保验证的公平性。

1.2 高光谱植被指数的计算及其波段选择

选取4种具有代表性的VI用于水稻LAI高光谱遥感估算，包括归一化植被指数(Normalized differential vegetation index, NDVI)、修正比值植被指数(Modified simple ratio index, MSR)、增强型植被指数(Enhanced vegetation index, EVI)和修正三角植被指数2(Modified triangular vegetation index 2, MTVI2)，如表1所示。

采用前人研究中提出的默认波段，计算高光谱VI。按以下步骤，选取高光谱波段组合来计算各个VI(记为VIopt)[10-11,27]。首先，采用如下光谱范围内所有可能的波段组合计算目标VI。Rblue：420～ 490nm，Rgreen：500 ～ 590 nm，Rred：630 ～ 720 nm，RNIR：720～1220 nm。其次，分析各波段组合计算的VI与实测LAI之间的相关性，得到VI-LAI关系矩阵。最后，选取产生最大相关系数(Correlation coefficient,R)的波段组合作为计算该VI的优选波段组合。针对本研究采用的4个VI，利用样本量不同的3套训练样本，分别开展波段选择。

表1 植被指数及其表达式

1.3 LAI统计估算模型构建

为了探索VI波段选择对LAI反演的影响，基于样本量为72的训练样本，利用默认和优选波段组合，计算NDVI、MSR、EVI和MTVI2。分别将上述VI之一作为自变量，对应的实测LAI为因变量，利用指数回归(ER)和人工神经网络(ANN)构建LAI单变量统计估算模型。为测试训练样本量对LAI反演的影响，再分别基于样本量为48和24的训练样本，重复上述试验，但仅利用优选波段组合计算的VI之一作为自变量。

本研究选用的ER和ANN分别是极具代表性的一元参数回归算法和机器学习回归算法，均广泛应用于LAI遥感估算[7],ER模型见公式(1)。

LAI=α×exp(b×x)

(1)

式中，a和b为模型参数，本研究利用最小二乘法求解；x为输入自变量(亦即VI)。

ANN是对人脑组织结构和运行机制的抽象、简化和模拟，通常由输入层、输出层以及1个或若干个隐含层构成，可以逼近任意连续函数[28]。本研究使用反向传播(Backpropagation，BP)神经网络模型。该模型属于多层状型的ANN，每一层包含若干神经元(节点)，层与层之间的神经元通过连接权重及阈值互连，每层神经元的状态只影响下一层的神经元状态，同层的神经元之间没有联系(图2)。BP 神经网络利用训练样本数据，采用误差逆传播算法(Error back propagation)修正网络权值和阈值，使网络实际输出值和期望输出值构建的误差函数(损失函数)沿负梯度方向下降到最小，从而获得满足需求的网络模型[29]。

图2 BP神经网络结构Fig.2 BP neural network structure

表2 ANN超参数设置

本研究中，ER和ANN均利用Python语言(Scikit-Learn软件包)[30]编程实现。利用网格搜索法对ANN模型超参数(表2)进行组合调优；通过k折交叉验证法(取k=15)确定最佳超参数值组合。k折交叉验证即将训练样本集随机划分为k个子集，每次使用k-1个子集训练模型，剩余1个子集进行验证。交叉验证重复k次，取k次精度指标的平均值作为该套超参数值组合的精度。

1.4 LAI估算精度评价

LAI估算完成后，采用测试样本LAI估算值与实测值之间的决定系数(Coefficient of determination,R2)和均方根误差(Root-mean- square error, RMSE)作为LAI估算精度的评价指标。R2表征实测LAI估算值与实测值之间的线性拟合优度(Goodness of fit)，R2越接近1，LAI估算的准确率(Accuracy)越高,表示LAI估算值与实测值之间的差距越小，估测精度(Precision)越高。

(2)

(3)

2 结果与分析

2.1 高光谱植被指数优选波段组合

从表3可知，优选波段组合与前人提出的默认波段组合间存在明显差异：优选近红外波段为1110或1115 nm，适用于全部VI；优选红光波段为720或675 nm(因VI而异)。EVI的蓝光波段以及EVI和MTVI2的红光波段的优选波段与默认波段较接近。基于不同训练样本量得到的优选波段组合差异极小。仅有基于24与48个(以及72个)训练样本选出的MTVI2红光波段存在 45 nm的差异。

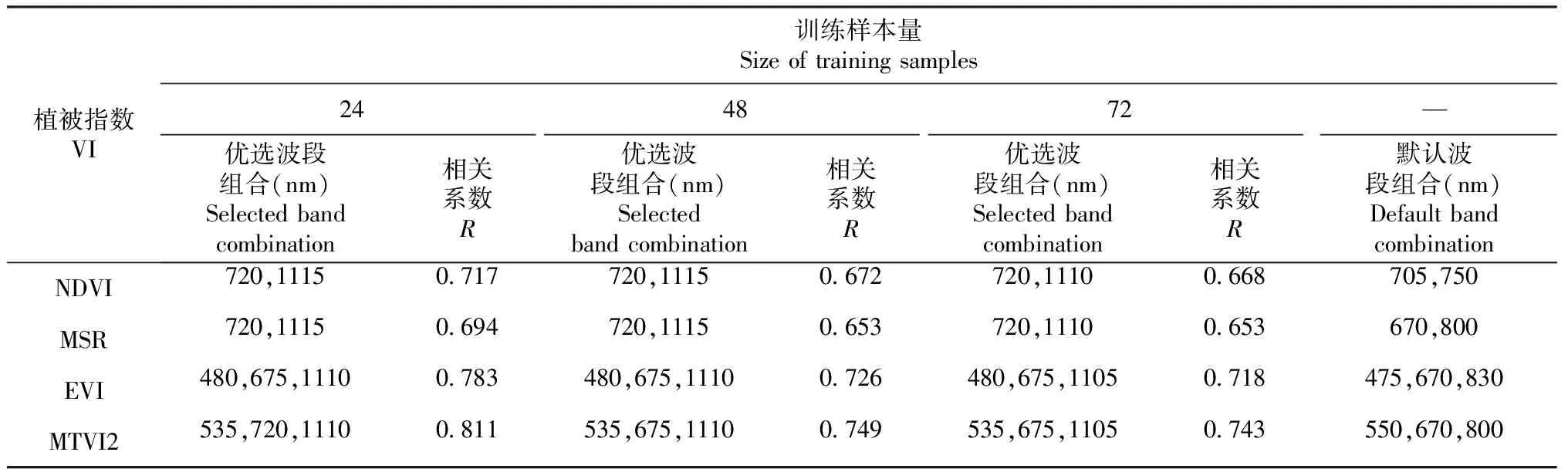
表3 基于不同训练样本的VI优选波段组合及VIopt与LAI的最大相关系数

2.2 LAI反演精度及其影响因素分析

2.2.1 植被指数选择对LAI反演的影响 为探索VI波段选择对反演精度的影响，基于样本量为72的训练样本，利用默认和优选的波段组合，计算NDVI、MSR、EVI和MTVI2，并分别构建LAI单变量统计估算模型。采用默认波段组合计算的VI按照其LAI估算精度升序排列，依次为NDVI、MSR、MTVI2、EVI(图3)。利用ANN模型，基于后一个VI的RMSE较前者的降幅依次为13.09%、3.73%、2.58%。采用优选波段组合计算的VI按照其LAI估测精度升序排列，依次为MSR、NDVI、EVI、MTVI2。利用ANN模型，基于后一个VI的RMSE较前者的降幅依次为0.82%、8.58%、6.32%。由此可见，无论是否开展波段选择，基于EVI和MTVI2的反演结果均优于NDVI和MSR。可能是因为不同VI 随LAI的增加而“饱和”的程度不同。当LAI≥2时，ANN和ER模型都低估了LAI(图4-a、4-b、4-e、4-f)。除了一定程度上的模型拟合能力不足的影响，该现象直接原因即为NDVI和MSR的“饱和”。相对而言，EVI和MTVI2(图4-c、4-d、4-g、4-h)虽然低估了LAI，但程度较弱。

2.2.2 植被指数波段选择对LAI反演的影响 对比图3～4可知，不论基于何种VI，采用何种回归建模方法，基于优选波段组合的反演结果(平均R2为0.574，平均RMSE为0.598)均优于基于默认波段组合的结果(平均R2为0.424，平均RMSE为0.694)。针对各个VI而言，利用ANN模型，经过波段选择后，基于MSR、NDVI、EVI、MTVI2的LAI反演值与实测值之间的R2较波段选择前分别提高24.73%、11.73%、60.62%和9.38%；RMSE分别降低16.29%、8.28%、18.22%和5.12%。此外，VIopt-LAI之间的R(表3)与对应的LAI反演精度基本呈正相关。由此可见，依据VI与LAI之间的关系矩阵选择VI最优波段组合的方法是可靠的。

基于样本量为72的训练样本;ANN_NDVI 表示基于NDVI，利用ANN模型的LAI反演，以此类推Experiments illustrated above were conducted using training samples of which sample size is 72; ANN_NDVI means the result based on NDVI and ANN model, etc.图3 基于各个VI默认波段组合的LAI反演精度Fig.3 Accuracies of LAI estimations based on VIs computed using their default band combination

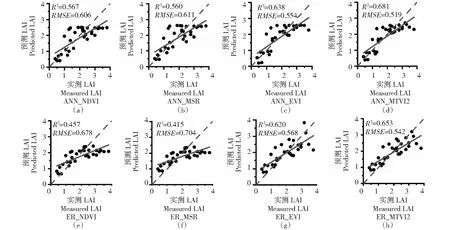
基于样本量为72的训练样本;ANN_NDVI 表示基于NDVI，利用ANN模型的LAI反演，以此类推Experiments illustrated above were conducted using training samples of which sample size is 72; ANN_NDVI means the result based on NDVI and ANN model, etc.图4 基于各个VI优选波段组合的LAI反演精度Fig.4 Accuracies of LAI estimations based on VIs computed using their selected band combination

2.2.3 建模样本量对LAI反演的影响 为研究训练样本量对LAI反演精度的影响，基于样本量为24和48的训练样本构建LAI估算模型，测试样本固定不变。由图4和表4可见，当训练样本量低至24时，基于EVI构建的ANN模型仍可取得较好的测试精度(R2=0.660, RMSE=0.537)，仍然优于ER模型(R2=0.597, RMSE=0.585)。上述现象表明，训练样本量对LAI反演精度影响不明显。

2.2.4 回归建模方法对LAI反演的影响 基于样本量为72的训练数据，较之ER模型，计算利用ANN模型带来的R2与RMSE变化百分比(表5)。可知，ANN模型得到了更高的R2(意味着LAI遥感估算值与实测值一致性更高)与更低的RMSE(意味着LAI遥感估算值与实测值间误差更小)。该规律在建模样本量较小的情况下依然存在。尽管波段选择对基于ER模型的LAI估算精度提升更为明显，但基于ER的精度仍逊于ANN。

表4 基于不同训练样本量的LAI估测精度

表5 ANN模型对LAI反演精度改进的百分比(相较于ER模型)

3 讨 论

3.1 关于表征LAI的特征参量

(1)鉴于表征LAI的特征参量对于反演精度有明显的影响。因此，应更广泛地尝试各种VI、红边参量、光谱主成分等多种光谱特征参量，择其优者作为LAI的特征参量。或者充分利用机器学习适于拟合高维度、非线性关系[7]的优势，将一种或多种类别的单一光谱特征参量组合成为表征LAI的特征向量，以期减小VI“饱和”问题对LAI反演的影响，提高LAI估算精度。

(2)根据VI“饱和”现象的特点，可以考虑将LAI的取值范围划分为几个较小的区间，分段开展特征参量选择和LAI估算模型构建。在作物长势正常的情况下，影响LAI的主要因素为作物的生育期(物候期)。目前，涉及生育期对LAI遥感估算影响的研究较少，结论也不尽相同[10,31-33]。将来可以尝试构建针对单一生育期的LAI估算模型，缩小LAI的取值范围，有可能减少VI“饱和”问题的影响。

3.2 关于植被指数波段选择

本研究表明，位于红边的720 nm有时比默认的670 nm更适于作为 “红光”波段(Rred)，用于计算NDVI和MSR，进而估算LAI。该结果与Wang等[10]、林卉等[11]，以及Hansen和Schjoerring[34]的结论一致。因此，在基于VI的LAI遥感估算的波段选择中，应将红边波段加入VI的Rred的备选波段范围。同时，优选的近红外波段为1110或1115 nm，位于水分吸收带附近。该现象可能与稻田水体对太阳辐射的吸收有关。鉴于本研究的实验规模，1110或1115 nm能否作为水稻LAI、覆盖度等几何结构参数的特征波段，仍有待后续更为全面和定量探索。

3.3 关于样本量的影响

本研究中，训练样本量对LAI反演精度未产生显著的影响。这与机器学习需要较大的训练样本量的一般认识不尽相符。究其原因，首先，本研究总的训练样本量及不同训练样本之间样本量的梯度均较小，可能不足以充分体现样本量的影响。其次，本研究验证样本量较小，反演精度评价结果可能存在偏差。尽管如此，本研究仍可看作一个特例，即使基于较小的训练样本，机器学习算法仍有可能得出较好的LAI估测结果，且优于参数回归。在未来研究与遥感数据产品生产中，可以更多地尝试基于小样本机器学习的LAI遥感监测，以测试相关方法的应用潜力。为了更全面地评价建模样本量的影响，有必要基于足够大的建模和训练样本开展试验；或借用k折交叉验证的思路，不断交换训练样本与验证样本，以平均的R2和RMSE来评价样本量的影响。

4 结 论

表征LAI的VI及其波段选择，以及回归建模方法均对LAI遥感估测精度有较为明显的影响。鉴于此，针对特定区域的目标作物，尝试利用任意可能的波段组合来计算多种VI，遴选与LAI相关系数最大的VI及其波段组合，有益于提高基于VI的LAI高光谱遥感估算精度。其间，采用红边波段代替默认的红光波段计算的VI有可能更好地表征LAI。此外，即使基于小样本训练数据，机器学习算法仍有可能得出优于参数回归的结果。

未来，应尝试更为广泛的光谱特征参量，或尝试构建表征LAI的多维特征向量，以发挥机器学习算法的优势，提高LAI反演精度。同时，可以尝试针对目标作物关键生育期，分别建立LAI估算模型。并应进一步探索基于小样本机器学习的作物参数遥感估算。