基于地面光谱测量和主动微波遥感的反演土壤水分研究

尹承深，刘全明，王春娟，王福强

(内蒙古农业大学水利与土木建筑工程学院，呼和浩特 010018)

【研究意义】传统的土壤水分监测主要依靠大量野外布点采样与事后数据处理、分析，但其以点代面、费时费力并且无法代表大面积动态实时监测效果[1]。大面积动态监测灌区土壤水环境对科学指导盐碱化严重的河套灌区农业可持续发展具有重要意义[2]。受植被覆盖、云层和大气干扰因素的影响，根据标量辐射方程，仅能记录较少地面物体信息的反射辐射能量[3]，导致光学遥感反演土壤水分的精度无法达到要求。因为微波波段土壤介电常数和含水量关系密切[4]，主动微波遥感能够通过后向散射系数反演水分，微波遥感-合成孔径雷达是对地观测的主要前沿技术之一[5-7]。【前人研究进展】刘伟[8]运用L波段全极化影像，在有植被土地的一阶离散植被模型上把有低矮植物土地的后向散射分为两块：地表与植被相关的散射项，结合光学厚度、植被层单散射反照率与裸露地表参数，利用改进的积分方程、Dobson与Ulaby的农作物覆盖模型，建立后向散射模拟数据库。在此基础上应用基于特征根与特征向量的极化分解方法将地表散射项从植被覆盖区总后向散射中分离出来，利用多时相、多极化数据建立了植被覆盖的水分反演模型。实测验证表明：该方法考虑了植被-土壤间的双次散射，可以较好地反演土壤水分[9]。Bourgeau-Chavez等[10]利用Radarsat-2雷达卫星构建了阿拉斯加地区土壤水分反演算法。李相等[11]通过获取102个土壤含水率数据和34组植被反射率光谱曲线，运用多元线性回归法构建了基于遥感影像与田间实测数据的高光谱植被指数土壤含水量反演模型。结果表明实测高光谱植被指数模型较优，判定系数0.668。刘全明等[12]采用野外试验、数据分析、遥感反演建模相结合的方法定量估计河套灌域表层土壤水盐含量，但未扩及至多源遥感数据协同模拟研究。郭交等[13]基于哨兵数据，利用广义神经网络模型、支持向量回归、Oh模型定量反演土壤水分，发现加入海拔高度、双极化雷达后项散射系数、局部入射角等多特征参数组合的支持向量回归模型反演效果最优，相关系数、均方根误差为0.903、0.015。刘晓静等[14]以高光谱数据为基础建立基于植被指数土壤含水率模型，发现以植被指数为VOG1和mNDVI705的模型估算最佳。张晓光等[15]采用高光谱技术建立与含水率的偏最小二乘回归模型，发现平滑+变量归一化后的光谱模型可以直接用于盐渍土水分的反演。【本研究切入点】现有的土壤水分遥感反演研究大多建立理论、经验或半经验的散射模型，模型受极化方式、地表粗超度、波段、入射角和植被覆盖等因素的限制[16]。为此需要研究如何融合地面高光谱与微波遥感多源数据，创新土壤水分监测应用的新方法和新手段。【拟解决的关键问题】采用高光谱土壤水分特征波段，联合后向散射参数，建立以多源遥感为基础的水分反演模型及人工智能模型，从而将多源遥感参数转换为水分值，为反演土壤水分提供科学基础，以提高土壤水分监测的精度与广适性[17]。

1 材料与方法

1.1 研究区概况

河套灌区位于40°12′～41°20′N，106°10′～109°30′E。该区地形较为平坦，海拔约1007～1050 m。年降水量为100～250 mm，蒸发量高达2400 mm，温带大陆性气候。灌区灌溉面积5583 km2，不仅降水少而且蒸发量大、土壤次生盐渍化现象严重[18]。

1.2 数据获取与处理

研究区为巴彦淖尔市的解放闸灌域，试验时间2016年4月4—8日。遥感数据是2016年4月6日RADARSAT-2雷达卫星拍摄的精细四极化SLC影像[19]，8 m的分辨率。结合土壤盐分统计资料选取89个采样点，制定采样路线，采样点分布见图1。实验过程中通过手持GPS仪测量各采样点经纬度坐标，利用剖面板上有厘米网格的方法测量地表粗糙度，测量过程详见王学[9]的方法，在各个取样点及其左右5 m处共取土壤表层土(0～10 cm)3份土样装入编号铝盒，烘干法测定土壤含水率，取平均值得到最终各点土壤含水率。

在SAR Scape模块对雷达数据进行如下操作：多视、滤波、地理编码和辐射定标[20]，在相关影像对雷达数据几何配准，获得四极化后向散射系数[21]，研究区部分取样点后向散射系数、地表粗糙度与含水率值如表1所示。

Field Spec4便携式光谱仪用于取样点土壤反射率光谱数据的采集，详细采样过程见孙宇乐[22]的方法。在光谱仪本身自带软件中将光谱反射率R变换3种不同形式：一阶导数、二阶导数和以10为底的对数形式，输入数据是3种变换光谱及地面反射率，后期将4种输入值与对应取土点位含水率进行相关性分析[23]。

图1 研究区雷达影像Fig.1 Radar image of experimental area

表1 雷达影像后向散射系数与土壤含水率原始数据

1.3 数学方法

主成分回归(Principal component regression, PCR)、多元逐步回归分析法(Multiple stepwise regress, MSR)、偏最小二乘回归(Partial least squares regression, PLSR)详见冯雪力等[23]的方法。BP人工神经网络(Back Propagation Artificial Neural Network, BP ANN)详见刘全明等[24]的方法。

BP ANN模型综合土壤含水率、地表粗糙度ZS、高光谱光学特征波段、后向散射系数(SHH、SVV、SHV、SVH)存在明显响应关系，输入层由SHH、SVV、SHV、SVH、SHH/SVV、SHV/SVH、地表组合粗糙度和光学特征波段反射率变换值组成；输出层是1个神经元与各点含水率对应；隐含层神经元个数根据试算法结果来确定。由Matlab中的神经网络工具箱来完成运算，训练值70%，验证值15%，模拟值15%。

前3种方法从众多波段筛选出特征波段，利用特征波段构建经验模型和人工智能预测模型，反演土壤水分。

2 结果与分析

2.1 特征波段选取

从图2可以看出，土壤含水量与光谱的一、二阶导数有较高的相关性。发现在一阶导数变换的1188～1192、1191～1193、2167～2171和2184～2188 nm相关性较高，为-0.46、-0.46、0.52和0.57。二阶导数的450～454、1412～1416、1421～1425、2208～2212 nm的相关系数为0.50、-0.49、0.55和-0.59，4个波段相关性较高，为显著波段。

图2 光谱及其变换形式对土壤水分的相关系数Fig.2 Correlation coefficient between soil moisture and 4 forms of spectra

对光谱的一、二阶导数特征波段进行主成分分析(图3)，一阶导数的1个特征波段累积贡献率可达98.32%，二阶导数的2个特征波段的累积贡献率为96.89%；其中，第一主成分一阶导数变换特征波段(2184～2188 nm)与二阶导数变换特征波段(2208～2212 nm)的特征值为1.19E-5、2.01E-7，因子贡献分别达到98.32%、90%，皆具有较高代表性，为显著波段。

逐步回归分析光谱一、二阶导数特征波段，光谱一阶导数的2184～2188 nm特征波段与二阶导数的450～454、1412～1416、2208～2212 nm特征波段为显著波段。

偏最小二乘法选择特征波段及拟合土壤含水率，用波段权重值表示波段对含水率的敏感度。该方法选取的波段不同于前两者回归分析方法选择的波段(图4)，有极为敏感波段，如一阶导数中1800～1870 nm波段权重达1.3，二阶导数变换中1835～1839与1870～1874 nm权重分别可达-6.6和-6.2，为显著波段。

从表2可知，相比一阶倒数变换，二阶导数拟合度更好，RMSE均有下降，显示出二阶导数变换拟合含水率较合适。对比光谱形式二阶导数的3种方法，可见逐步回归分析法效果最好，R2、RMSE为0.482、0.027，主成分分析法次之，偏最小二乘法最差。因此可以选择前两者来建立方程。

2.2 建模

对主成分回归和逐步回归分析法选取地表组合粗糙度、特征波段反射率与后向散射系数及其组合值，建立含水率和二阶导数的回归方程。

(1)

式中，X1414、X2210分别为光谱二阶导数1412～1416、2208～2212 nm的波段的算术平均数。

图3 特征波段的主成分分析Fig.3 Principal component analysis of characteristic bands

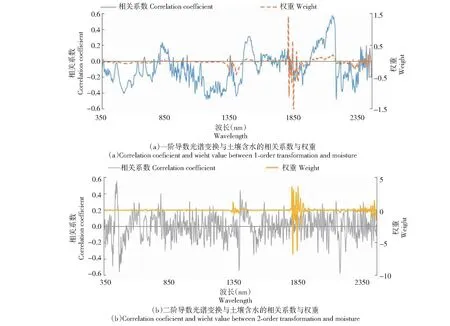
图4 土壤含水率和反射率导数变换的偏最小二乘法权重和相关性Fig.4 Analysis of weight between reflectance derivative transformation and soil moisture

表2 相关系数法与偏最小二乘法拟合结果对比

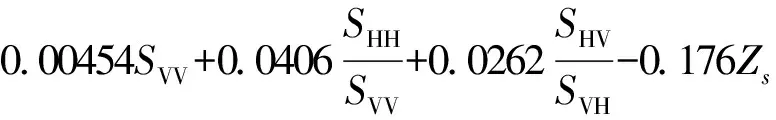
(2)

式中，X452、X1414、X2210分别为光谱二阶导数450～454、1412～1416、2208～2212 nm波段的算术平均数。

同时建立神经网络模型，由图5-c可知，神经网络模型R2值为0.792，远高于上述相关系数法光谱二阶导数的回归方程，体现了神经网络模型的优越性。

2.3 土壤水分预测

按照土壤含水率(0～50 g/kg)每5 g/kg划分一类，共划分10类的分类方法，将河套灌区盐渍化土壤进行分类。逐步回归分析法建立的回归方程模拟的土壤含水率如图6所示，模拟结果如表3所示。可见，研究区整体土壤含水率较高，主要分布在20～25 g/kg，占全局的70.44%，这可能是研究区内土壤盐碱化程度较为严重的一个主要原因, 在今后的土地治理及农业生产活动中要着力降低土壤的含水率, 以保证农业生产的可持续发展。

图5 土壤含水实测与模拟值Fig.5 Measured and simulation value of soil moisture

图6 研究区土壤含水量反演Fig.6 Inversion result of soil moisture image in study area

表3 土壤含水率反演分类占比

3 讨 论

在土壤水分反演过程中，相比于多元逐步回归分析，BP神经网络方法在精度上更高，其R2为0.792，这与孙宇乐等[25]R2达到0.796及王启元等[26]R2均值达到0.754的研究结果基本相同。其原因可能是土壤光谱信息与土壤性质之间不是单一的线性关系，SMLR模型只能进行线性回归预测，而BPNN模型同时具备线性和非线性处理能力，因而模型精度更高。

分析中对光谱反射率做数学形式的变化后，有效地削弱遥感影像中噪声的影响，提高与土壤含水率的的相关性优于原始数据，这与马驰[27]、李鑫星等[28]、赵飞飞[29]、Yin等[30]的研究观点相同。

本研究认为土壤含水量的特征波段为450～454、1412～1416、1421～1425、2208～2212 nm。姚艳敏等[31]认为400～410、1400～1850、2050～2200 nm为吉林黑土含水量敏感波段；张锐等[32]认为原状水稻土水分敏感波段集中在1450、1950和2220 nm附近；于雷等[33]认为浙江土壤水分敏感波段为443～449、1408～1456、1916～1943、2209～2253 nm；尚天浩等[34]通过逐步回归分析与灰色关联度分析法筛选出宁夏银北地区盐碱化土壤水分的敏感波段集中在1460、1950和2200 nm附近；韩陈等[35]认为1400、1900、2200 nm为紫色土和黄壤含水率敏感波段。以上研究与本研究水分敏感波段基本一致，其中与姚艳敏等[31]的研究结果更为接近，但在不同土壤类型下，各研究者所提取的具体波段均有所不同。除土壤本身性质影响外，研究区域、采用的分析模型方法、光谱获取方式及筛选方式等有所差异也有较大影响。

下一步盐碱地水分遥感预测模型须加强和中高分辨率卫星光学影像的结合，针对植被覆盖条件下的灌区土壤条件，试验多尺度、多时相的多源遥感大数据动态监测，能够对大区域盐碱地水分的准确反演[36]，以丰富灌区土壤墒情监测的技术手段。

4 结 论

通过不同形式的光谱变换处理可以使光谱反射率与土壤含水量的关系得到提升，相关性较好的是光谱一、二阶导数，特别是二阶导数的450～454、1412～1416、1421～1425、2208～2212 nm 4个波段相关性高，相关系数分别为0.50、-0.49、0.55和-0.59。PCR二阶导数变换的1412～1416、2208～2212 nm 2个特征波段累积贡献率为96.89%；MSR二阶导数的450～454、1412～1416、2208～2212 nm 3个特征波段为显著影响波段；PLSR筛选的特征波段较主成分分析以及逐步回归分析法选取的波段有所不同，且存在极为敏感的波段，如二阶导数变换中1835～1839与1870～1874 nm权重值较大。

通过协同河套灌区解放闸灌域盐渍化土壤光谱特征波段反射率二阶倒数、雷达后向散射系数及其组合与地表粗糙度，对比含水率的PCR、MSR与PLSR 3种反演模型，发现MSR模型的R2、RMSE为0.482、0.027，优于另外2种模型。而BP神经网络模型最佳，R2为0.792。