安全级DCS机柜抗震性能时程分析及试验研究

代俊安，魏新宇，王东伟，胡利鸿，吴 霄，刘 丽

(1.西安交通大学 能源与动力工程学院， 西安 710049；2.中国核动力研究设计院 核反应堆系统设计技术重点试验室， 成都 610041)

0 引言

核安全级数字化控制系统(digital control system， DCS)对核电厂的运行工况进行监测，同时在事故工况下驱动相应的设备执行保护功能，以确保反应堆、核电厂设备、人员和环境的安全。考虑到核电站通常建立在沿海地震频发地带，且由于福岛事故的恶劣影响，核安全级DCS系统机柜在地震工况下保持结构和功能的完整尤为重要，因此抗震性能是考核DCS机柜结构设计可靠性的关键因素之一[1]。

目前，关于核安全级DCS系统机柜的抗震分析得到了国内外核工业领域研究者的大量关注[2-8]。Tran等[2]使用对数正态法构建出核电仪控机柜的易损性曲线，重点探讨了构成易损性曲线的各关键要素对机柜抗震性能的影响。Lin等[3]采用了类似简化的弹簧—质量模型，模拟了在地震作用下核电仪控机柜内部响应特性，计算结果与试验结果匹配较好。Cho等[5]使用梁单元简化机柜受力模型，并充分考虑非线性因素对模型的影响，大大节约计算资源和减小计算量，并且成功预测了机柜的振动模态和相应的地震响应行为。考虑到响应谱分析法难以对机柜的高频模态响应进行评估，Gupta等[6]提出了Ritz向量法用于评估机柜的高频动态响应。刘明星等[7]采用响应谱法对机柜进行校核，而后进行抗震试验分析机柜的结构响应特性与抗震性能，研究结果表明抑制机柜的横向运动是改善结构抗震性能的关键。

上述研究为认识核电机柜的抗震性能研究提供了重要参考依据。但是上述研究通过响应谱分析法计算机柜结构的整体应力，无法探究机柜的振动响应特性。而通过试验研究，相关工作[7]未对机柜的振动信号、演变特征进行深入探讨。因此，有必要进一步对机柜在地震动工况下的行为进行分析，探索结构可能存在的振动演变特征，并将仿真分析结果与试验研究进行对比，揭示机柜受到地震激励下的响应行为，从而为机柜的结构设计和抗震性能评价提供更为可靠的理论依据。

基于以上研究，本文结合响应谱分析法和时程分析法对核安全级DCS系统机柜进行仿真分析，在认清结构频率响应和时程动态响应特征的基础上，严格按照核电设备试验标准对机柜样机进行抗震试验。进一步地，对仿真与试验结果进行对比分析探讨，揭示机柜结构的地震响应特征。本研究结果能为后续的机柜设计和分析研究提供参考和理论依据。

1 机柜有限元模型及边界条件

核安全级DCS系统机柜主要由焊接框架、柜门、机箱和柜内安装零部件组成。焊接框架采用厚度为2.5 mm的Q235B(密度7.8 g/cm3、弹性模量205 GPa、泊松比0.3)钢板折弯焊接而成，其主要承力结构由上围框、下围框、左侧片和右侧片构成，三维模型如图1所示(X为横向、Y为纵向、Z垂向)。基于三维模型，建立机柜的有限元模型如图2所示。

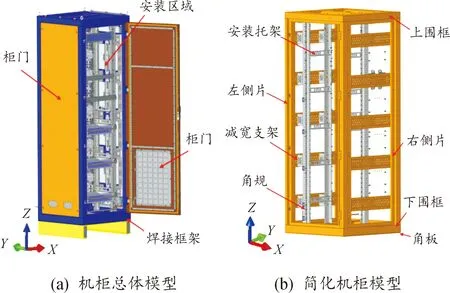
图1 机柜三维模型

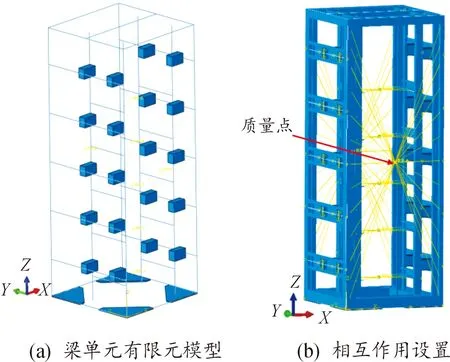
图2 机柜有限元模型

为了节省计算资源，需对有限元模型进行简化处理，具体如下：

1) 焊接框架、内部安装部件、角规和托架等采用梁单元，并对零部件设置相应的属性。

2) 减宽支架采用壳单元。

3) 在机柜的柜门、机箱和其他部件相应位置设置参考点，将参考点与焊接框架的壳单元耦合，对参考点设置相应的质量值，并以模拟相应配置的重量，得到有限元模型质量为500 kg。

4) 结构之间的螺接简化为固定约束，并约束机柜底部所有方向自由度。部件网格特征如表1所示。

表1 部件网格特征

进一步地，通过质量矩阵和刚度矩阵的组合确定结构的瑞利阻尼，包含α和β两个参数[11]，如式(1)所示：

[C]=α[M]+β[K]

(1)

式中：α为质量阻尼系数；β为刚度阻尼系数。α和β的简化计算公式分别为：

(2)

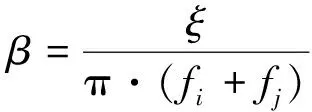
(3)

式中：fi为第i阶阵型的固有频率；fj为第j阶阵型的固有频率；ξ为阻尼比。本文中使用结构第1阶和第2阶阵型的固有频率。

2 有限元分析

2.1 模态分析

首先对机柜进行模态分析，结构模型的前10阶自然频率分布如图3所示。可见机柜的前10阶模态频率与振型相对独立，不存在相邻自然频率非常接近的现象，这在一定程度上避免了模态集中可能存在的振动放大等问题。对机柜的前3阶模态进行分析，结果见图4，机柜在底部约束状态下的第一阶模态振型表现为机柜整体沿X方向的偏摆运动，频率为9.258 7 Hz；第2阶整体模态振型是机柜整体沿Y方向的偏摆运动，频率为26.617 Hz，第3阶整体模态频率为29.24 Hz，模态阵型表现为机柜框架整体沿Z方向的扭转运动。

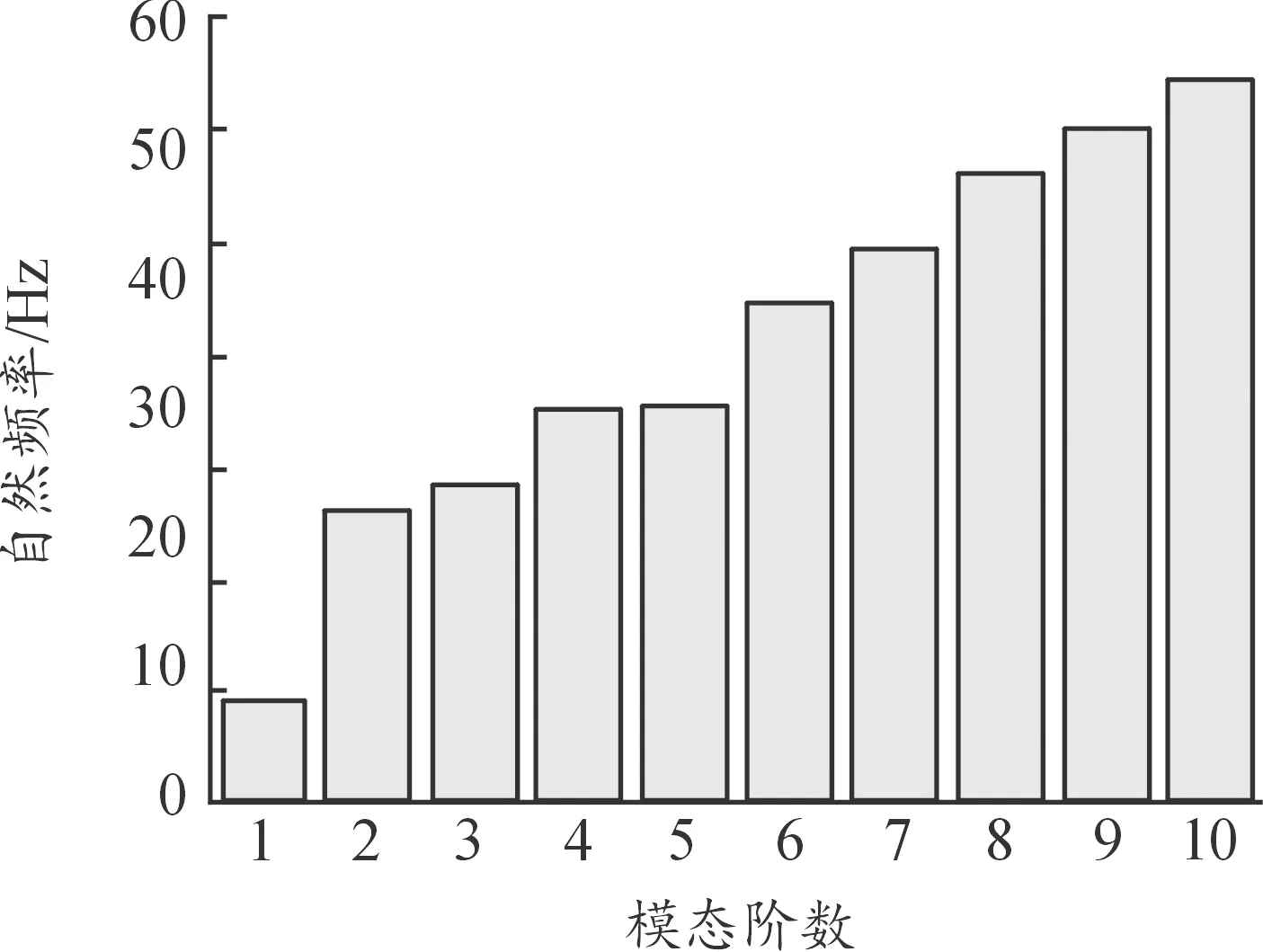
图3 机柜自然频率分布图

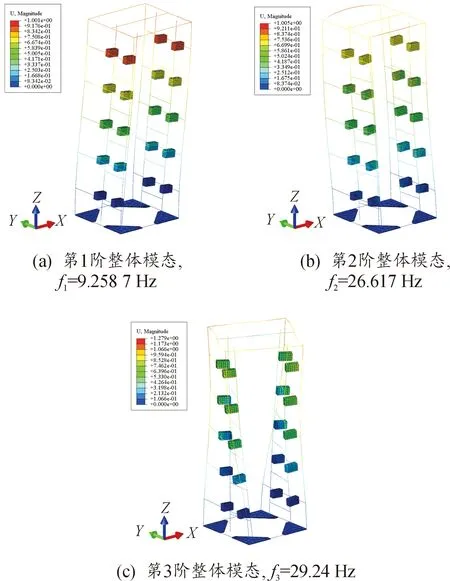
图4 机柜前3阶模态阵型

考虑到机柜所在地区地震响应谱的幅值放大区域通常集中在2～10 Hz[12]，而机柜的第1阶频率位于该放大区内，因此，无法通过简单的模态分析对机柜的抗震能力进行判断，故需进行进一步分析和探讨。

2.2 响应谱分析

考虑到在后续实际试验过程中，机柜需要依据标准HAF J0053分别进行5次OBE(运行基准地震)试验和1次SSE(安全停堆地震)试验(阻尼比取5%)[12]。考虑到SSE地震响应谱在水平和竖直方向的信号均能包络OBE的响应谱，因此，在仿真中以SSE地震作为计算的地震响应谱计算的输入。另外，鉴于机柜在核电站现场的具体安装方向未定，因此使用水平X、Y方向合并绘制的水平包络谱进行水平方向上的计算，图5为SSE在阻尼比为5%时水平(X、Y向)和竖直(Z向)2个方向的地震响应谱曲线。采用响应谱分析法中的SRSS(square root of the sum of squares)对机柜在地震作用下的响应进行分析[7]，计算结果如图6所示。可以看出，机柜在地震载荷作用下，呈现出的最大Mises应力为151.7 MPa，位于前门右立柱底部。这是由于机柜的第1阶模态表现为沿X向的左右偏摆运动，同时由于机柜前侧布置机箱及各类器件，使得整体重心前移，因此机柜前端底部承受较大的应力，导致该处应力最大，但该最大应力值小于Q235B的屈服极限235 MPa，因此在该地震激励作用下，机柜具有较好的抗震能力，不会出现明显的塑性变形和开裂等现象。机柜的最大位移出现在其顶部区域，最大位移值为16.4 mm，这也是机柜在地震信号作用下第一阶模态特性导致的。

图5 SSE地震响应谱曲线

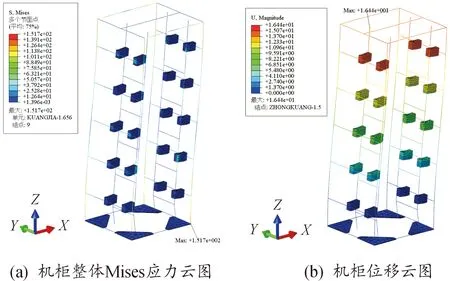
图6 机柜地震应力云图和位移响应云图

考虑到机柜在实际使用过程中，机柜内安放有重要的电子器件和众多功能PCB板块，因此，在明确机柜结构的承载能力和抗震能力后，有必要对机柜结构在地震激励下的时程响应信号进行进一步探究，从而根据响应信号对电子设备的安装位置和可靠性进行深入判断。

2.3 时程分析

2.3.1时程分析原理

采用ABAQUS隐式求解器对机柜在地震激励下的信号演变进行分析求解，系统的动力学平衡方程可以表达为：

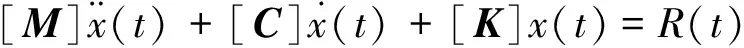
(4)

式中：[M]为结构质量矩阵；[C]为结构阻尼矩阵；[K]为结构刚度矩阵；x(t)为振动幅值矢量；R(t)为外部载荷。

假定在时间间隔[t,t+Δt]内，加速度线性变化，即速度和加速度公式可表示为：

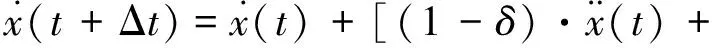
δ·x(t+Δt)]Δt

(5)

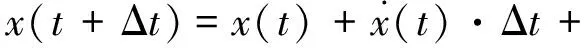
(6)

式中δ和ε是按积分的精度和稳定性要求可以调整的参数。

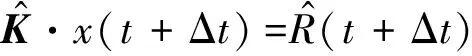
(7)

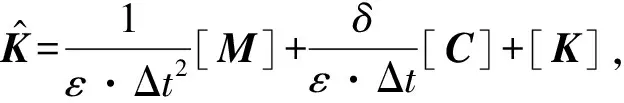
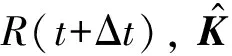
2.3.2时程输入信号

对图5中的地震响应谱进行时程转换，结果如图7所示。需要说明的是，输入时程是通过RRS(要求反应谱)用计算机生成的SSE状态下的人工模拟加速度时程，在生成人工模拟加速度时程时，对要求反应谱考虑了10%的裕量，时程持续时间为30 s，强震时间超过15 s。计算时程时反应谱的频率间隔为0.1 Hz，满足HAF·J0053[14]建议的用于计算要求楼板反应谱的频率间隔的要求。生成的SSE人工模拟加速度时程3个方向之间的相关系数如表2所示，各向之间相关系数满足HAF·J0053中小于0.3的要求。

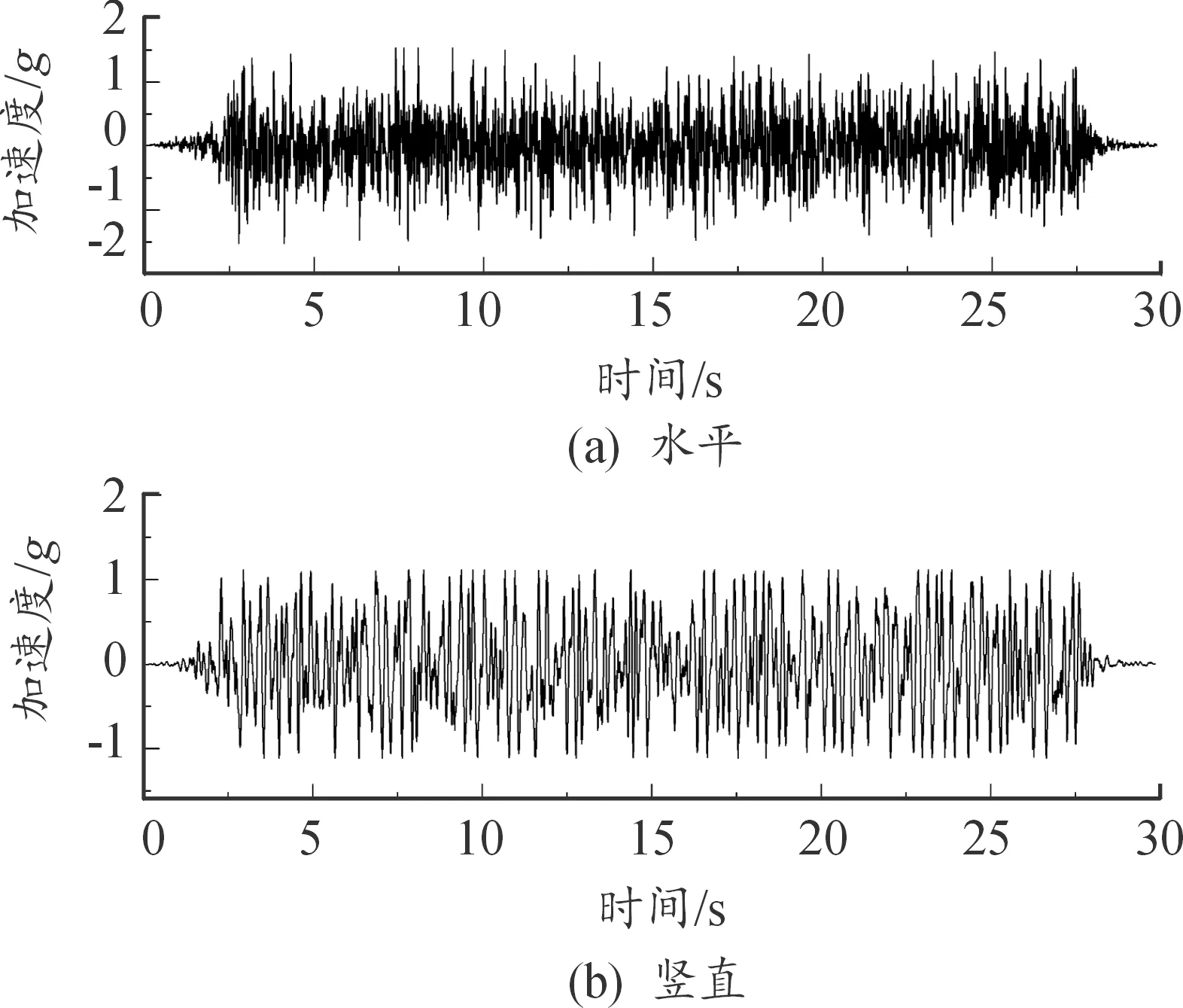
图7 SSE地震试验输入时程

表2 SSE 3个方向之间的相关系数

将3个方向的时程曲线(SSE状态下)加载到模型上，并在有限元模型上建立如图8所示的3个观测点(F1，F2，F3)，所建立的观测点位置与后续试验中加速度计安装位置保持一致。计算得到各测试点的加速度幅值时程曲线如图9所示，计算得到各测试点的最大加速度幅值如表3所示。

图8 仿真观测点位置

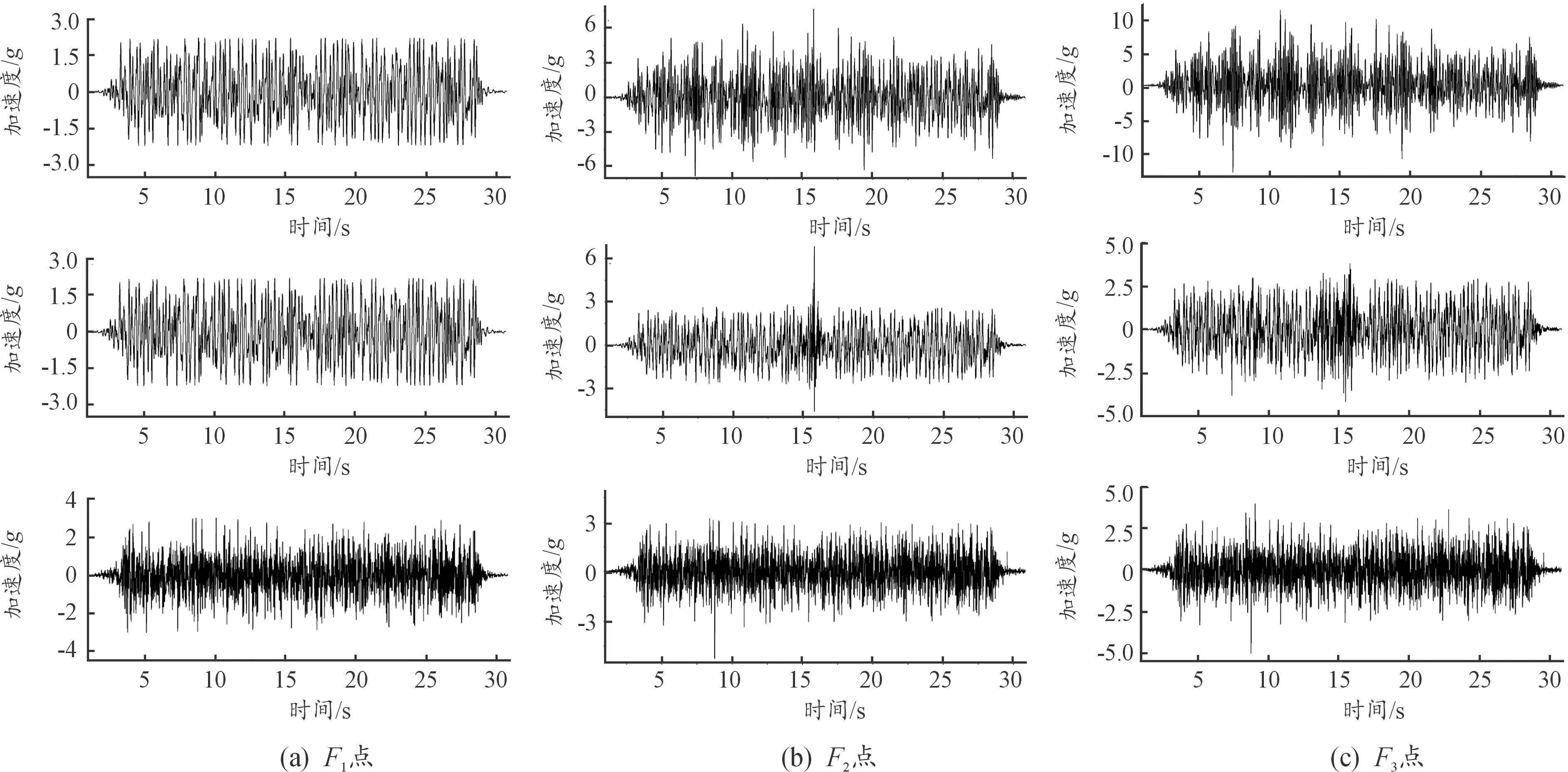
图9 各观测位置的三向加速度时程图

表3 时程分析各测点的加速度响应最大值 g

可以看出，振动台面上的观测点(F1)在3个方向的振动幅值均是最低的，这时由于机柜底部测点距离振动台面较为接近，直接接收来自台面的振动信号，因此机柜底部的振动幅值相较于振动台面基本无明显增大。

在X方向上，台面振动随着机柜高度的上升，经过一定的放大传递到机柜的重心，后传递至柜顶。随着振动信号向上传递，机柜的振动加速度幅值逐渐增大，其中最大加速度幅值(F3点处)为地面振动加速度幅值(F1点处)的5.87倍。相比之下，机柜结构在Z(垂向)向上的振动放大非常微弱，这也说明地震动在垂直方向对机柜的影响相对较弱。因此，纵向运动和横向运动对机柜的振动响应影响较大，其中抑制横向运动是改善结构抗震性能的关键[7]。

3 地震试验分析

3.1 试验流程与设备

在数值模拟的基础上，本研究依据HAF·J0053等相关鉴定试验标准，进一步开展机柜的地震相关试验研究。地震试验在最大承载60 t的6 m×6 m大型高性能地震模拟试验台上进行，试验台水平方向的最大位移±150 mm，竖直向最大位移±100 mm，水平向和垂直向满载最大加速度分别为1.0、0.8g，地震输入频率范围为0.1～100 Hz。试验中采用Kistler公司生产的8395M06型加速度计测量台面和被试设备上的运动加速度，使用LMS数据采集仪采集加速度数据。

试验首先需搭建测试环境及安装机柜。目视检查机柜结构完整后，将机柜焊接到底座钢板上，底座钢板与地震试验台通过M30地脚螺栓螺栓刚性连接。在机柜重心、顶部及地震台台面分别安装一组加速度传感器(X、Y、Z3个方向)。地震试验环境搭建示意图与真实试验照片如图10所示。实测试验机柜重量约为490 kg，与有限元模型质量500 kg非常接近。

图10 机柜地震试验示意图和照片

依据标准HAF J0053相关规定，试验流程如图11所示。首先通过动态测试对结构的自然频率进行分析。随后进行5次OBE试验，OBE试验时台面的加速度值是SSE试验的1/2倍，在完成OBE试验后，对机柜结构进行检查，确认结构框架无损坏后再进行SSE试验，SSE试验完成后再次检查结构框架。检查过程中若结构或焊缝出现撕裂、扭曲等现象，则试验结束，判定试验失败。

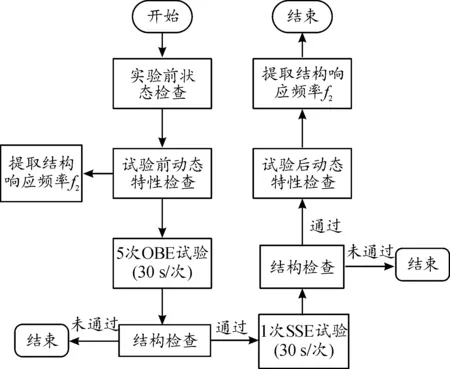
图11 核级电气设备地震试验流程框图

3.2 试验结果分析

3.2.1试验前动态特性分析

在机柜的3个正交轴向输入加速度幅值为0.2g的白噪声信号进行扫频，扫频范围为1～100 Hz，扫频速率为1 oct/min，持续时间为120 s。测试结果与模拟结果见表4。

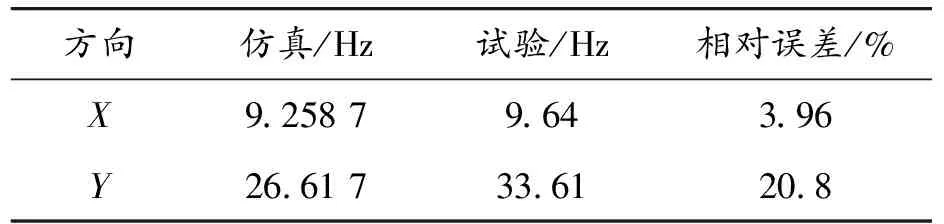
表4 仿真结果与试验结果相对误差

可见机柜的X向一阶固有实测频率为9.64 Hz，同计算所得的一阶频率9.258 7 Hz非常接近，误差为3.96%；相比之下，虽然Y向一阶实测固有频率为33.61 Hz，同计算所得的26.617 Hz存在一定的差异，这是由于机柜计算过程中对模型存在一定的简化，以及质量分配同真实设备存在一定的差异所导致。考虑到大于25 Hz的自然频率对地震响应的作用非常微弱，且实验和计算的模态振型二者具有很好的一致性，因此可以认为，本研究建立的有限元仿真模型能够真实仿真结构的动态特性。

3.2.2地震试验结果分析

地震试验在机柜样机的3个正交轴向同时进行激振。表5中列出了5次OBE和1次SSE地震工况下试验台面响应时程信号与输入时程信号之间的相关系数，可以看到相关系数均接近于1，即地震台的信号能够很好模拟地震试验的要求时程信号。

表5 台面加速度时程与要求加速度时程的相关系数

表6统计了各测试点在各个工况下的最大加速度响应，从表中可以看出，地震台台面的加速度幅值在3个方向均是最低，在地震试验过程中，地震信号通过地震台台面传递到机柜的各个位置，并在传递过程中加速度信号有不同程度的放大。该试验结果同模拟分析结果(图9)非常一致。

表6 地震试验中各测点的响应最大值 g

进一步地，将OBE试验各测点响应的最大振动加速度幅值进行统计，如图12所示。在X方向上，随着振动逐步向上传递，各测试点的振动加速度幅值逐步增大，其中A3点处的振动加速度振动幅值超过了台面A1点处振动加速度幅值的4.7倍，且各测试点在横向的振动放大最为明显。在Y方向上，随着机柜框架上测试点高度增加，结构振动加速度幅值逐步增大，但放大幅度较低，测点A3的振动加速度幅值约为柜底加速度的1.5倍。相比之下，在垂直方向上，各测试点的振动放大相对较弱。

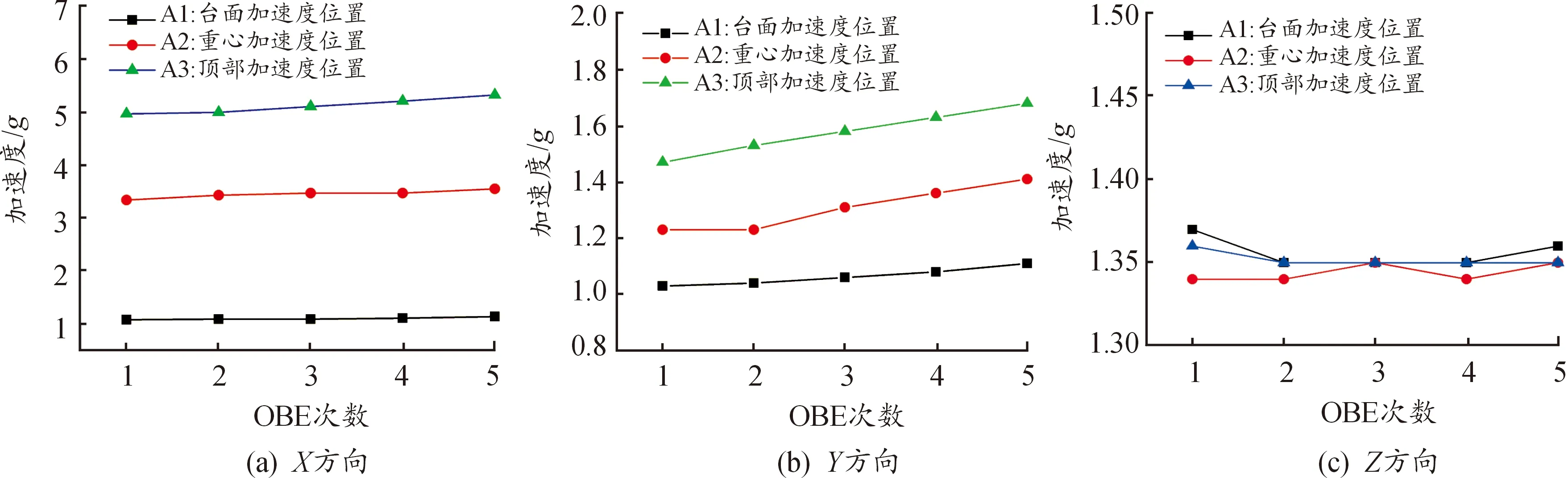
图12 5次OBE试验中结构各测试点3个方向最大加速度幅值

SSE试验的台面加速度值为OBE试验的2倍。从图13中可以看到， 机柜在X向振动强度增加显著，尤其A3点处的振动加速度振动幅值超过了台面A1点处振动加速度幅值的5.2倍。相比之下，Z向上机柜各测试点的振动加速度幅值的增益不明显，这也进一步说明，改善机柜结构的抗震性能主要需抑制机柜在X方向上的运动。对比测试点的仿真结果和试验结果可以看到，测试点仿真和试验的振动加速度最大值能够很好地对应，并且都是X向振动增益最为显著，证明仿真结果能够很好的预测机柜结构在地震工况下的振动特性。

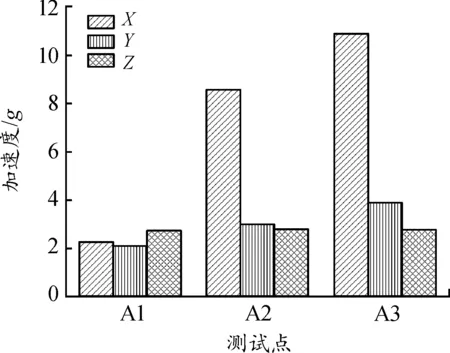
图13 SSE试验时机柜各测试点3个方向最大加速度幅值直方图

3.2.3试验后动态特性分析

SSE地震试验后，采用白噪声对该机柜进行动态特性检查。表8对比了机柜试验前后各方向的一阶固有频率及对应阻尼比，可见试验机柜在X方向的固有频率为9.64 Hz变为9.6 Hz，Y方向的固有频率由33.61 Hz变为33.79 Hz，Z方向的固有频率始终大于100 Hz，即各向固有频率均无明显变化。对被试机柜进行结构检查，机柜整体结构无变形和破裂，各个连接件无松动和脱落，被试机柜样机地震试验合格，从而证明本次研究设计的机柜具有良好的抗震性能。

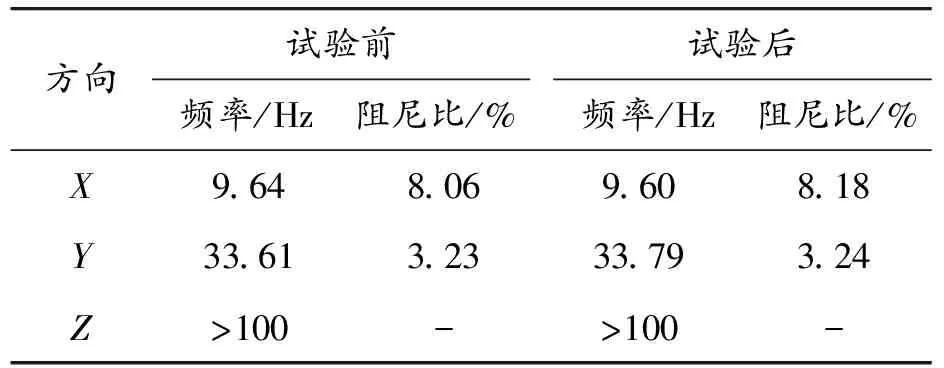
表7 试验前后机柜的动态特性参数

4 仿真与试验结果分析

4.1 高度对结构振动的影响

4.1.1高度与振动加速度关系

根据时程分析结果，绘制3个观测点的加速度时程曲线如图9所示，对应的振动加速度均方根值见表8。可见机柜横向和纵向的振动加速度的均方根会随着机柜的高度增加而增加，在横向方向上，加速度均方根随高度方向的变化趋势为先快速放大，随后放大趋势随高度逐渐变缓；柜底到重心位置加速度均方根放大了约2.03倍，从重心位置到柜顶加速度均方根放大约1.62倍。在纵向Y方向上，加速度均方根值会随着机柜的高度增加而增加，但增大幅度较小，维持在1.05倍。综合分析和试验结果，可知随着机柜高度增大，机柜水平方向上的加速度会呈现递增趋势，横向X方向加速度均方根随高度方向的增大趋势为先快后缓，而纵向方向加速度振动强度呈均匀递增趋势。基于以上分析，建议在后续设计中考虑对机柜框架横向X方向的刚度进行加强，增加框架横向支撑，增加机柜顶部与底部的连接位置的柔性过度，从而减小横向加速度放大幅度。

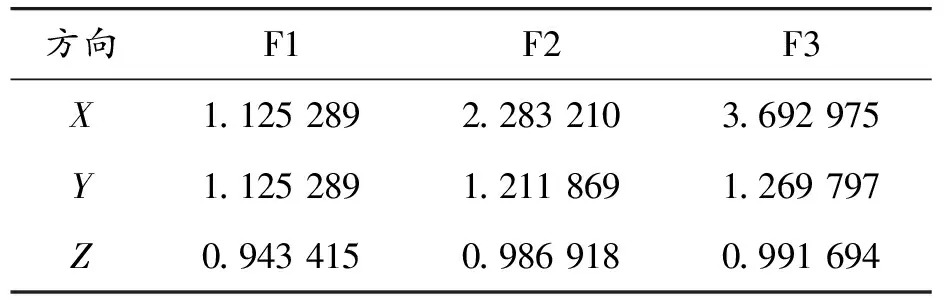
表8 各观测点的时程加速度的均方根 g

4.1.2高度与频谱关系

由于机柜重心上下两侧布置了多个功能机箱，且柜顶布置有机柜的散热系统和保护性的电气件，故有必要对重心附近区域和柜顶区域的结构响应特性进行深入讨论。本研究选取F2和F3点的横向振动加速度信号进行时频分析，结果如图14所示。

图14 X向时频图

可以看出，2个区域的振动时频信号存在显著的差异，柜顶处F3点的振动能量明显强于机柜重心处。另外，可见当机柜横向振动在5～10 s过程中，机柜在5 Hz附近存在明显的多频振动现象；当振动持续进行时，振动能量有所减弱；但是当振动持续至20 ～25 s过程中，机柜结构响应在3 Hz附近处出现明显的振动能量集中现象。综合以上，柜顶处的振动强度明显强于机柜重心处，且机柜振动的演变存在多频且时变的特性，在振动初期，振动强度持续增大，多频振动现象出现；在振动后期，随着阻尼对能量的耗散以及振动趋于稳定，结构在某些特定的频率处存在能量明显集中的现象。基于以上分析，建议在后续设计中增加机柜框架上部刚度，以减小柜顶振动强度，规避振动初期的低频状态的多频振动现象和振动后期的振动能量集中现象。

4.2 机柜底部受力对安装影响

机柜通过焊接方式固定在核电厂指定厂房的预埋件上，机柜在地震工况下产生的反作用力大小会直接影响预埋件的选型。各角板反作用力分布如图15所示，每块角板在机柜前后门方向上有两处较大的反作用力集中点，随着距离集中点的距离增加，反作用力不断减小。其中前门右下角和后门左上角的反作用力略大于其他角板。通过python脚本读取角板上各结点的反作用力，提取各节点RF python流程图如图16所示。

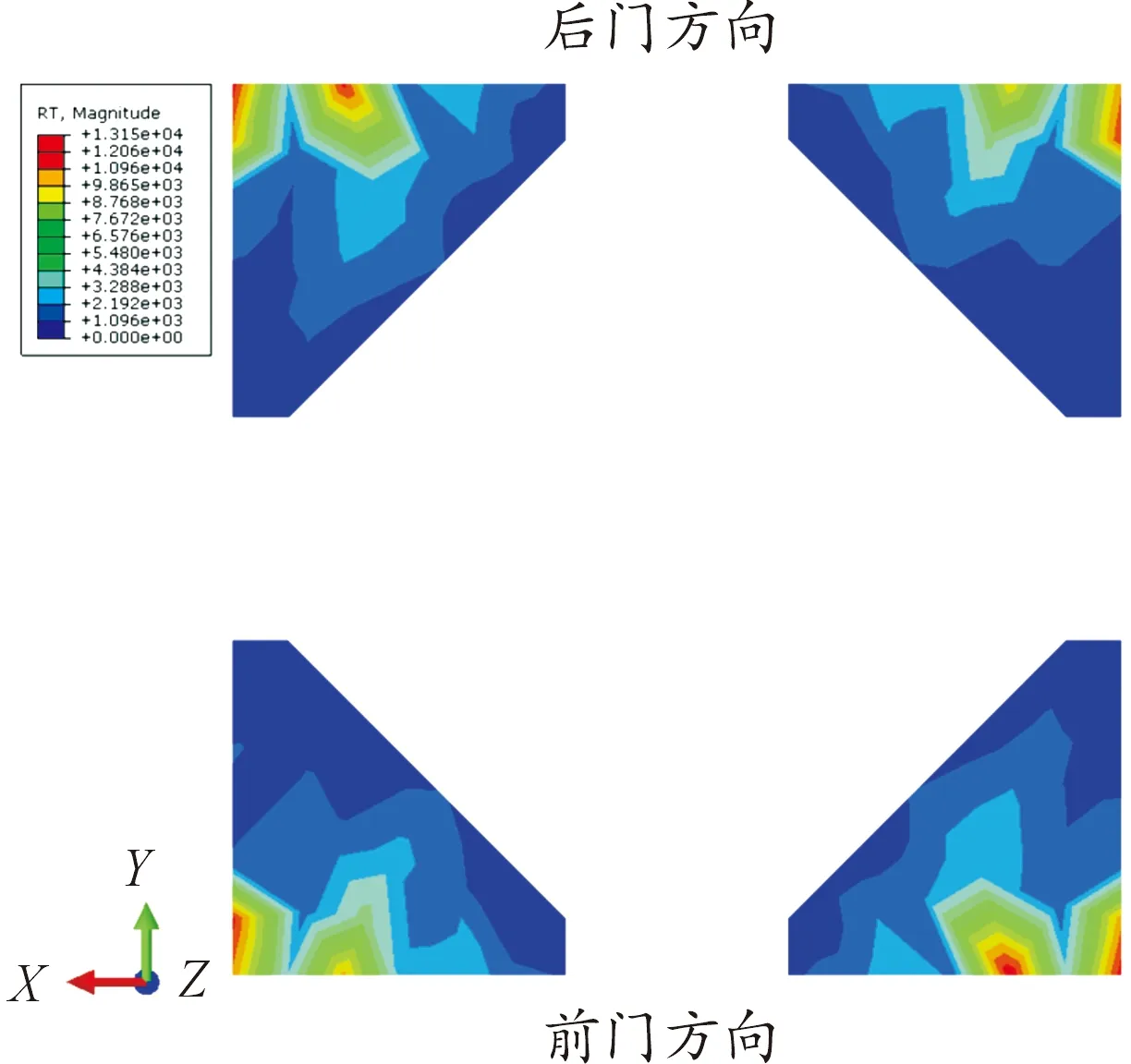
图15 角板反作用力分布图

图16 提取各节点反作用力python语句流程图

表9总结对比了机柜底部四角的反作用力，在机柜前门方向上的底部焊缝受到的反作用力与机柜后门方向相差较小。当前机柜配置的重量分布情况较为合理。反作用力的提供有助于后续预埋件的选型和安装提供参考。

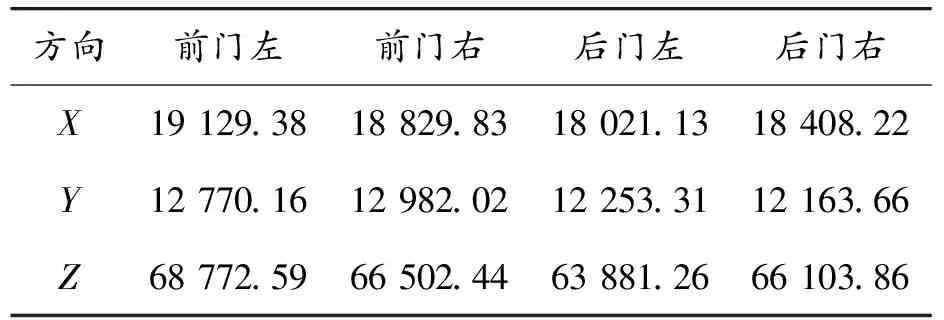
表9 机柜底部角板反作用力 N

5 结论

1) 安全级DCS系统机柜的一阶模态振型为机柜沿X方向的左右偏摆运动，频率为9.258 7 Hz。响应谱分析获得结构的最大Mises应力为151.7 MPa，位于机柜框架前门方向右下角，小于Q235B的最大屈服极限，因此机柜具备较好的抗震能力。

2) 时程分析结果表明，随着机柜高度增大，结构振动强度逐步增大，X方向(横向)上的振动幅值增益最为显著，机柜顶部处的振动加速度均方根为地面振动加速度均方根的3.28倍。相比之下，竖直Z方向上的振动加速度变化不明显。因此，抑制机柜横向运动是增强结构抗震性能的关键。

3) 时频分析结果表明，柜顶处的振动强度明显强于机柜重心处，且机柜振动的演变存在多频且时变的特性。在振动初期，结构在频率5 Hz附近处出现多频振动现象；在振动持续到后期，机柜在频率3 Hz出现明显的振动能量集中现象。

4) 通过时程分析法可获取机柜结构在地震工况中各时间点机柜的实际加速度大小、加速度变化趋势等，可分析机柜各频域的响应情况和能量集中情况。

5) 提取机柜底部4个角板的反作用力，机柜前门方向上的底部焊缝受到的反作用力与机柜后门方向相差较小，反作用力的提供有助于后续预埋件的选型和安装提供参考。

6) 仿真和试验的振动加速度趋势能够很好地对应。仿真结果能够很好预测机柜结构在地震动工况下的振动特性，试验结果确认了仿真结果的正确性，验证了机柜结构的抗震性能。该机柜的分析方法与试验流程和结果为核安全级机柜的后续深入研究提供了参考依据。