牌型预测与蒙特卡洛模拟结合的麻将博弈策略

李淑琴,冯浩东

(1.北京信息科技大学 计算机学院， 北京 100101；2.感知与计算智能联合实验室， 北京 100101)

0 引言

自古以来，博弈就是一个经典的研究领域，人类生活中每时每刻都在做着平衡与决策。每天的衣食住行、升学就业时的选择、购物消费时的优惠折扣、国与国之间的经济竞争和军事竞争，等等，这些问题场景都可以抽象成博弈决策问题。根据不同的角度，可以把博弈分为不同类型。根据博弈参与者对整个博弈状态的了解程度可以把博弈分为完全信息博弈和非完全信息博弈。在麻将游戏中，玩家只能看到自己的手牌信息和一些公共信息，而对手的手牌信息以及牌库中的信息都是不可见的。因此，麻将是典型的非完全信息博弈。

在完全信息博弈领域，当前最出名的是谷歌公司DeepMind团队开发的Alpha系列程序[1-4]，彻底击败了人类选手。与其不同，非完全信息博弈的解决面临诸多难题。第一，状态空间巨大。由于在非完全信息博弈中没有办法得知当前局面的全部信息，所以需要进行大量模拟来求解未知信息。非完全信息博弈的决策动作一般也不是固定的，例如德州扑克和斗地主中可以采取过牌操作，麻将中可以进行吃、碰、杠等操作，这都会使局面信息更加复杂。这些原因导致非完全信息博弈的状态空间非常庞大。第二，信息缺失。不同于完全信息博弈，非完全信息博弈的参与者并不知道对手的私有状态。这就意味着在完全信息博弈中的求解局部最优解方法不适用于非完全信息博弈，且没有办法准确评估自己在整个博弈局势中的优劣。例如在象棋、五子棋等完全信息博弈中可以通过搜索和遍历来得出最优决策，但这在非完全信息博弈上是不可行的。

在非完全信息博弈中，德州扑克是最受欢迎的研究对象。参考文献[5-7]使用反事实虚拟遗憾最小化算法在两人有限注德州扑克上取得了近似纳什均衡的效果。这是因为两人有限注德州扑克的状态空间小，因此反事实虚拟遗憾最小化算法是行之有效的。随后，卡耐基梅隆大学的TSandholm团队于2017—2018年提出了Libratus系列[8-9]程序，将改进的反事实虚拟遗憾最小化算法与安全子问题求解方法相结合解决了多人无限注德州扑克问题。Libratus没有采用当时流行的深度学习方法和神经网络模型，尽管取得了良好的效果，但是需要极大的计算资源。显然，德州扑克的解决方法在麻将这种状态空间爆炸的游戏中并不适用，因为其取得纳什均衡的成本是极其高昂的。

在麻将领域，Cheng等[10]在2017年使用数学模型通过基本组合理论研究麻将游戏。王亚杰等[11]根据先验知识和手牌信息给出麻将出牌决策，并使用蒙特卡洛模拟方法模拟对手手牌来防止点炮。虽然取得了不错的效果，但其核心方法是大量的领域知识模型。对于弃牌信息的利用率不高，也没有根据游戏状态来动态调整先验知识。针对非完全信息博弈和麻将游戏的特点，本文的工作目的就是充分利用麻将中的局面信息，尤其是弃牌信息，依此预测对手手牌和需求牌来缩减未知状态空间，从而降低麻将游戏的难度。并使用动态游戏状态划分方法适时调整局面信息利用方法，提升其准确性。将本文方法应用于麻将程序后，大幅提高了麻将程序的胜率，并降低了点炮风险。

1 麻将的规则和术语

麻将作为一项智力竞技运动，集益智性、趣味性、博弈性于一体。麻将自发明来一直深受社会各阶层的喜爱。

1.1 麻将规则

本文的研究对象为大众麻将，它是以国标麻将为基础简化而来。大众麻将的特点为牌型组合多、番型多，几乎涵盖所有麻将番型，十分考验麻将技巧与策略。牌库中有万、筒、条3种，点数分别为1～9，每个样式的牌有4张，总共108张牌。庄家起手14张牌，其他3位起手13张牌。行牌过程，可吃、碰、杠和听，并都可获得直接收益。行牌过程的优先级为：胡>杠>碰>吃。当有玩家成功胡牌或牌库摸完后，牌局结束并给出总分。

1.2 麻将术语

本节对后文中将要提及的术语进行统一解释。

顺子：3张连续的牌称为顺子；

相关组：2张连续的牌或间隔为1的2张牌称为相关组；

刻子：3张相同的牌称为刻子；

对子：2张相同的牌称为对子；

吃：当上一位玩家丢出一张牌，且可以与玩家手中的牌构成顺子时，可以吃牌；

碰：当其他玩家丢出一张牌，且玩家手中有2张相同的牌时，可以碰牌；

杠：当其他玩家丢出一张牌，且玩家手中有3张相同的牌时，可以杠牌；

副露：玩家吃、碰、杠后，可以被所有玩家观察到的牌型称为副露；

庄家：第一个打牌的玩家被称为庄家；

听牌：当玩家只剩一张牌就可以达到获胜状态时，可以宣布听牌；

向听数：向听数指玩家的手牌还差多少张牌可以听牌。

胡：当玩家组成获胜牌型，即4个顺子或刻子、一个对子时称为胡；

点炮：当玩家丢出的牌使对手达到胡牌状态时，称为点炮。

2 局面信息利用方法

在麻将中，因为玩家的弃牌与手牌具有一定的联系，玩家的信息会随着游戏进程的发展而不断暴露。在麻将中转换局面信息不仅可以帮助麻将程序做出更合理的出牌决策，也可以降低点炮风险，进而提高自己的收益。本文首先根据大众麻将领域知识提出弃牌信息利用方法和对手牌型概率计算方法，然后进行蒙特卡洛模拟得到对手的手牌分布，实现对麻将局面信息的最大化利用。

2.1 弃牌信息利用方法

本小节将把对手玩家的弃牌信息转换为可利用信息，并推算对手玩家持有某张牌的概率。在大众麻将中，同一花色的连续牌是具有强关联性的。针对大众麻将的规则特点，本文将在游戏的前后期采取2种不同的弃牌信息利用方法。

按照当前局面的情形，根据式(1)计算每一张牌的剩余牌数。

Ni=4-NOi-NMi

(1)

式中：Ni表示牌i的剩余张数；NOi表示对手弃牌中牌i的张数；NMi表示我方手牌及我方弃牌中牌i的张数。

大众麻将游戏前期，各个玩家都追求快速达到听牌状态，一般不会将关联牌拆分打出，所以前期的方法将围绕这一理念展开。与之对应，本文提出相依牌的概念。例如，若玩家丢弃某一花色的5点数牌时，其手牌中应该不会还有5，且在弃牌前应该没有「4、5」、「5、6」、「3、5」、「5、7」等组合牌。因此，若某一玩家弃牌中有5，应降低该玩家持有该花色牌中3、4、5、6、7的概率。其中，持有5的概率最小，其次是4和6、3和7。类似的，以此为依据可以得出相依牌表，如表1所示。表中相依牌与弃牌的相依程度依次降低，随着博弈的进行，相依程度还会进一步降低。此外，相依程度还与玩家的听牌时机高度相关，需要动态调整。

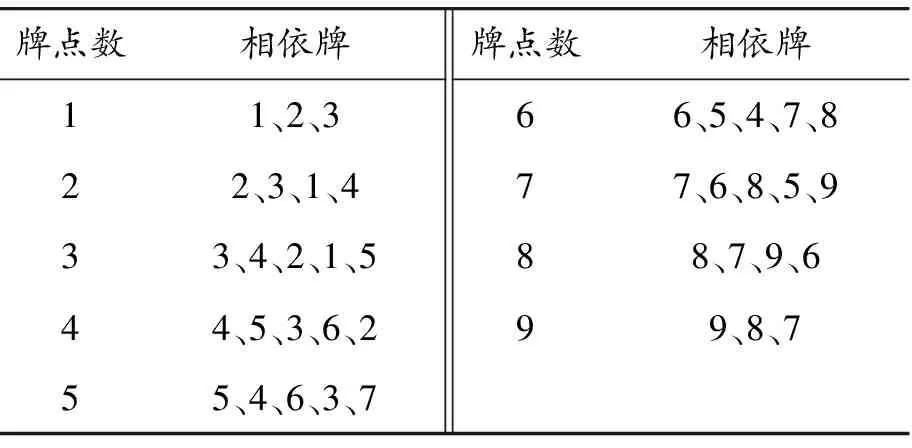
表1 相依牌表

根据弃牌的数量和相依程度，可以得到某一张牌对所预测牌的影响度。计算方式如式(2)所示,式中Ai, j指牌i对牌j的影响度，Ni指弃牌中牌i的张数，Ri, j指牌i与牌j的相依程度。

Ai, j=Ni×Ri, j

(2)

根据某一玩家的弃牌信息可以给出该玩家拥有某一张牌i的可能性PRi，计算方法如式(3)所示。当牌的点数不同时，其对应的相依牌数目也不同，因此式(3)按牌的点数将牌分为了5类。

(3)

游戏进入中后期时，玩家的手牌已基本成型，玩家丢出的牌多数都是与手牌无关的。当玩家弃牌时，理论上也不需要跟这张弃牌相关的牌。与之对应，提出非需求牌的概念。例如，由于1可以跟2、3组成顺子，当玩家打出1时，可能是该玩家手中并没有「2、3」这个组合，或是手牌中已有「1、2、3」的顺子，或是已经跟相邻的4组合成「2、3、4」的组合，而不论是上述哪一个状况，都可以推论该玩家对4的需求会降低。类似的，以此为依据可以得出非需求牌表，如表2所示。

表2 非需求牌表

非需求牌主要在防守阶段使用，通过其他玩家的弃牌信息来推算其不需要的牌，并且在游戏终盘时根据非需求牌调整手牌的权重分，使其他玩家不需要的牌更容易被打出去，挑选弃牌时的依据会从进牌收益最高的牌，变成兼具进牌收益与防守收益的牌，以此降低自己的点炮概率。

2.2 对手牌型概率计算方法

在2.1小节中，已经得到了玩家手牌中持有某张牌的概率计算方法。以此为依据，下面对玩家手中持有刻子、顺子、对子和相关组的概率进行计算。玩家手牌中拥有刻子牌型的概率计算方法如公式(4)所示。当牌A的数量小于3时，此时不可能存在由牌A组成的刻子；当牌A的数量大于等于3时，将根据牌A的数量和该玩家拥有该牌的可能性综合计算拥有牌A刻子的概率。玩家手牌中拥有顺子牌型的概率计算方法如式(5)所示。计算该玩家手牌中拥有顺子中每张牌的可能性，选最小值作为拥有该顺子的概率。与刻子和顺子不同，本文在对子和相关组牌型的概率值计算上还考虑了弃牌中其需求牌的非需求牌数量，若其需求牌的非需求牌数量很多，说明对手玩家手中有此牌型的概率极低，如式(6)—(8)所示。

(4)

PABC=min(PRA,PRB,PRC)

(5)

(6)

PAB=min(PRA,PRB)-(NN(A-1)+NN(B+1))/2

(7)

PAC=min(PRA,PRC)-NN(A+1)

(8)

式中：PAB指连续相关组的概率计算方式；PAC指间隔相关组的概率计算方式；NNi指的是牌i的非需求牌数。

至此，手牌中各种牌型的概率计算方法已经成型，但对手玩家手中各种牌型的数目仍然无法确定。接下来需要模拟对手玩家的向听数来确定玩家手牌分布。向听数将根据由大量真实对局数据得出的每轮向听数分布和玩家副露数计算得出，为

WN=1+GWN-F

(9)

式中：GWN指根据真实对局统计的向听数概率分布随机选择得到的向听数；F指玩家副露数。

2.3 对手手牌模拟方法

通过蒙特卡洛模拟方法来模拟对手手牌，不仅可以降低给对手打出需求牌的概率，还可以辅助判断我方的需求牌数量，使我方牌型更加合理，增加获胜概率。蒙特卡洛模拟是一种统计学方法，用来模拟大量数据。其核心思想就是通过模拟出来的大量样本集或者随机过程去近似想要研究的实际问题对象。对于那些由于计算过于复杂而难以得到解析解或者根本没有解析解的问题，蒙特卡洛模拟是一种有效的求出数值解的方法。

在麻将游戏初期，暴露的信息过少，若在初期进行蒙特卡洛模拟，只会增加模型复杂度而不会产生收益，因此蒙特卡洛模拟将在游戏中后期进行。下面给出基于局面信息和蒙特卡洛的对手手牌模拟算法流程，将整个模拟过程迭代X次至结果收敛便可以得出对手手牌，还可以根据对手手牌模拟剩余牌库分布。这样，麻将游戏中的信息不透明度会进一步降低，便于麻将程序对博弈局势做出更准确的判断。对手手牌模拟流程如算法1所示。

算法1对手手牌模拟方法

输入：我方手牌H，对手弃牌Di，对手副露Fi，轮数Round

输出：对手玩家的手牌分布DHi

01：根据式(1)计算每一张牌的剩余牌数Ni

02： while(X-->0) do

03：根据式(9)计算出Round轮的向听数WN

04：根据向听数WN，随机选择刻子数NAAA、顺子数NABC、对子数NAA、相关组数NAB

05：随机生成刻子、顺子、对子和相关组，根据公式(4)—(8)计算其持有概率，若概率极低则重新生成

06：根据随机结果更新DHi

07：end while

08：returnDHi

3 动态游戏状态划分方法

在麻将游戏中，玩家的出牌与出牌时的游戏状态是有密切联系的，合理的前后期游戏状态划分方法可以提高局面信息利用的准确率。在以往类似的研究中[12-13]，常常以对大量数据样本统计后的向听数为1时的最大轮数分布为游戏前后期界线。该方法虽然可以代表多数情况，但其对于部分牌局情况的适应性较差，会降低局面信息转换的准确性。所以本文提出了一种动态划分游戏前后期界线的方法，可以根据当前局面信息对游戏前后期做出更为合理的分界，这会进一步提升局面信息的利用效率，从而提高麻将程序的出牌水平。

和以往的方式不同，本文以动作数为标准划分游戏前后期，而不是游戏轮数。此处的动作包括摸牌、吃牌和碰牌。本文统计了3 000局真实对局中4位玩家每次动作后的向听数分布，统计结果如图1所示，频次指在对应动作数下的指定向听数出现次数。从图中可以看出，部分牌局在执行一次动作后，就有玩家达到了1向听状态。显然，如果只依据向听数为1的最大轮数分布进行前后期划分，将使麻将程序进入歧途。而且在执行动作3、4、5、6次后，都有很大概率达到1向听状态，显然不能仅仅以1向听的最大分布动作数4为前后期分界。

图1 大众麻将中向听数随动作数变化的分布图

根据大众麻将的游戏规则，吃、碰动作对向听数的影响远大于摸牌操作。因此本文还对吃、碰动作进行了额外的分析，统计了3 000局真实对局中4位玩家每次吃、碰动作后的向听数分布。因为在执行一次吃、碰动作后4向听的频次极低，因此在统计时将其忽略，最终的统计结果如图2所示。从图中可以看出，当玩家执行2次吃、碰动作后，向听数基本在2及2以下。

因此，本文将以向听数为1时的最大分布动作数4为前后期分界基准，以每轮游戏中玩家的吃、碰动作次数为辅，对每轮游戏中各个玩家的前后期界线进行动态划分，如式(10)所示。式中Di指针对i玩家的游戏前后期分界动作数，CPi指玩家i的吃碰次数。

Di=4-(CPi-1)

(10)

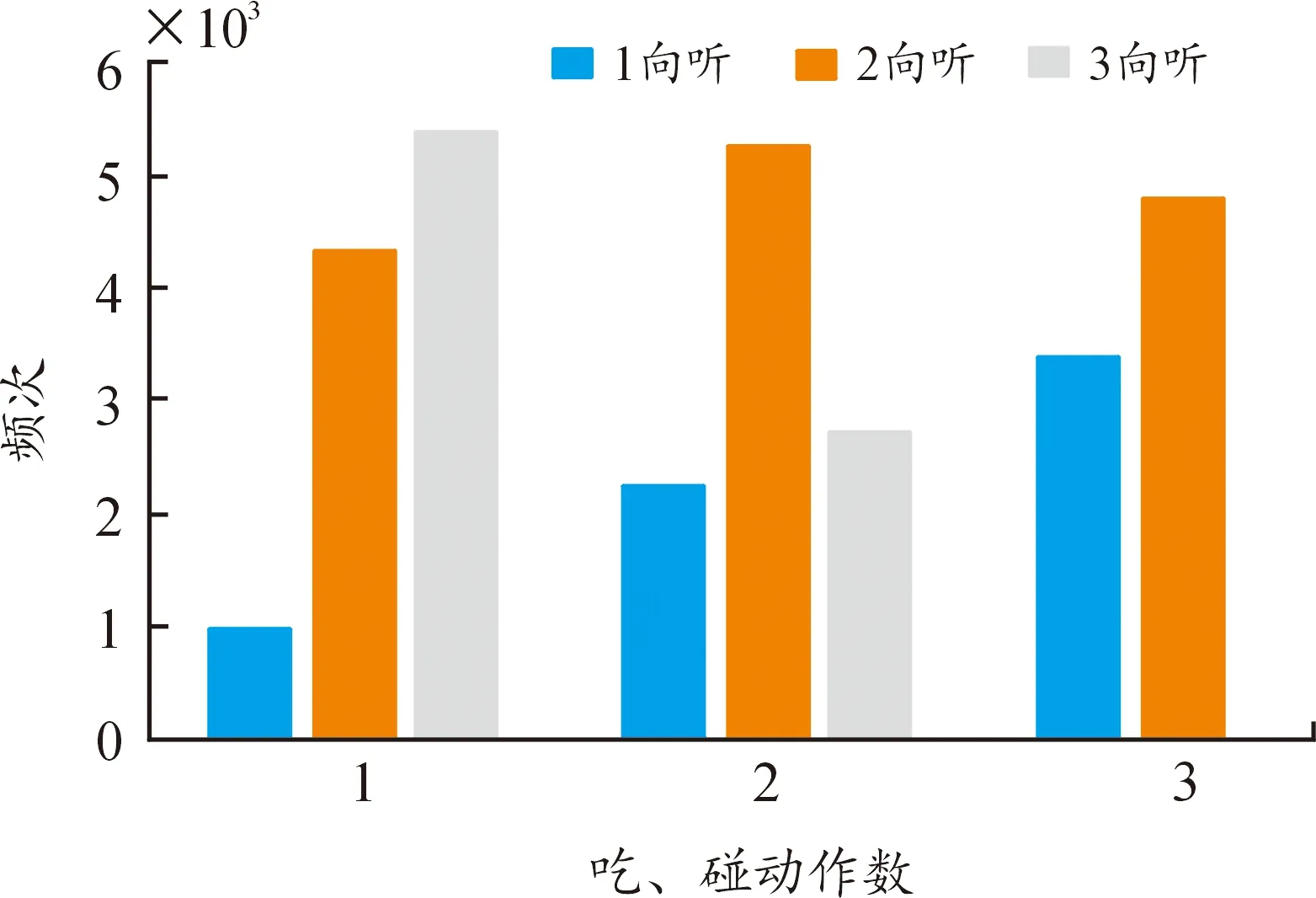
图2 大众麻将中向听数随吃、碰动作数变化的分布图

4 实验结果与分析

本文结合局面信息利用方法和动态游戏状态划分方法构造了一个麻将AI程序，为了证明其可靠性，在本节进行了大量实验。在每轮对局中，采用2+2的对战策略，即2位使用A方法的麻将程序和2位使用B方法的麻将程序进行对战。为了消除麻将游戏中靠运气取得胜利的因素，本文设定了1 000局对局为标准来验证各个方法的有效性。根据麻将规则，玩家只能吃上家的牌。因此需要考虑不同程序之间的座位顺序，在实验时通过调换每轮游戏中麻将程序的座位顺序加以解决。为了便于对比，将2个使用相同程序的对局结果累加，将点炮率、获胜率和得分作为比较标准，给出实验结果。

4.1 对比实验

4.1.1局面信息利用方法的影响

正如前文所说，局面信息利用方法的目的是通过转换局面信息降低麻将游戏局面的不透明度，从而提高麻将程序的出牌水平，并降低麻将程序的点炮率。为了证明其有效性，本文将其与传统的使用追求快速听牌方法的麻将程序[14-15]进行对比，将2个使用本文方法的麻将程序和2个使用传统方法的麻将程序进行了对战，结果如表3所示。容易看出，使用局面信息利用方法的麻将程序得分大幅领先于使用追求快速听牌方法的麻将程序，在点炮率和获胜率上都优于追求快速听牌方法的麻将程序。

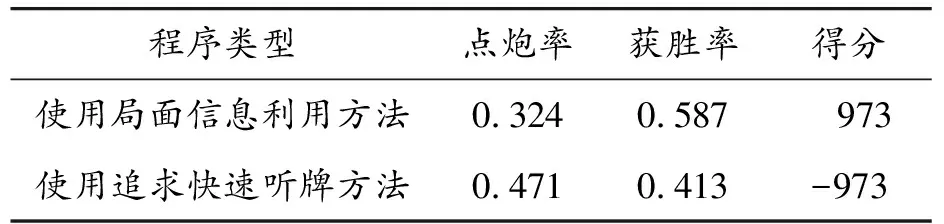
表3 局面信息利用方法的影响

4.1.2动态游戏状态划分方法的影响

为了证明动态游戏状态划分方法是必要的，本节将动态游戏状态划分模块替换为传统的静态麻将对局前后期划分方法进行对比试验。使用统计数据中向听数为1时的最大动作数分布，即玩家采取第4个动作时为前后期分界，在这里将之称为静态游戏状态划分方法。每场比赛包括2个使用动态游戏状态划分方法的麻将程序和2个使用静态游戏状态划分方法的麻将程序，结果如表4所示。使用动态游戏状态划分方法后，点炮率大幅下降，其获胜率和得分也随之提高。此外，使用静态游戏状态划分方法的麻将程序在游戏后期常常会做出不符合游戏规则的决策，这与其对游戏局面信息的错误利用有关，而动态游戏状态划分方法避免了这一问题。

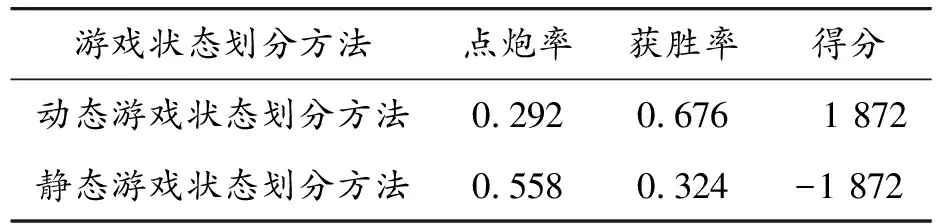
表4 游戏状态划分方法的影响

4.2 与高水平麻将AI之间的比赛

本节使用本文方法构建的麻将程序与在2020年中国计算机博弈锦标赛麻将项目中取得冠军成绩的程序[11]进行了比赛，每场比赛包括2个使用本文方法的麻将程序和2个冠军程序，统计了不同程序的点炮率、获胜率和最终得分。该冠军程序针对麻将游戏规则设计了一种基于弃牌优先级表的麻将决策方法，为不同牌型设定了不同的弃牌先后顺序。实验结果如表5所示，得益于本文的局面信息利用方法，使用本文方法的麻将程序点炮率相比冠军程序降低了11.9%，获胜率提升了7.6%。这表明使用本文方法构建的麻将AI达到了较高水平。

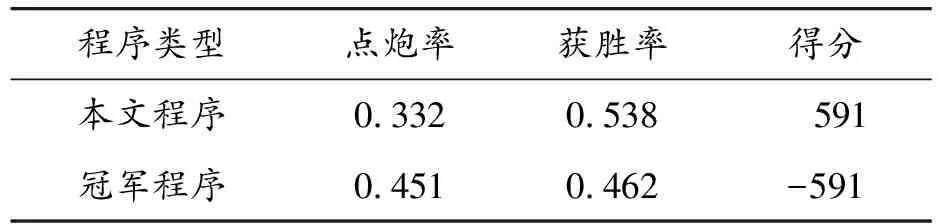
表5 与高水平麻将AI比赛

5 结论

本文提出了多种方式来充分利用麻将游戏对局信息，并使用动态游戏状态划分方法划分游戏前后期，以保证弃牌信息利用方法、对手牌型概率计算方法和对手手牌模拟方法的准确性。实验结果显示，本文的方法最大程度利用了麻将游戏中的局面信息。但是这些方法都是根据大众麻将的游戏规则而设定的数学模型。为了摆脱人类知识的局限性，今后将尝试结合深度学习方法，将数学模型与神经网络模型相结合，使麻将程序的出牌决策更加合理。