一种多重优先经验回放的麻将游戏数据利用方法
李淑琴,李 奕
(1.北京信息科技大学 计算机学院, 北京 100101; 2.感知与计算智能联合实验室, 北京 100101)
0 引言
计算机博弈一直是验证人工智能理论的试金石,也是人工智能最活跃的研究领域之一。计算机博弈相关理论和技术被广泛应用于金融、交通、军事等领域。计算机博弈通常包括完全信息博弈[1]和非完全信息博弈[2]。非完全信息博弈问题相对于完全信息博弈,其研究更为困难也更加具有挑战性。深度强化学习凭借深度学习的感知能力与强化学习的决策能力成为解决非完全信息博弈问题的主流方法[3-5],目前深度强化学习的研究点主要集中在样本利用效率,奖励函数设计以及决策方法上。
在样本利用方面,以往的经验回放机制中最早采用的随机经验回放,即将多条经验样本存储在经验池中,然后随机采样更新深度神经网络,以便克服数据之间的相关性,这在一定程度上提高了数据利用率,但不符合人的学习习惯。人们在日常的学习中,往往对一些重要的经验记忆深刻,而忽略那些不重要的经验。文献[6]首次提出了优先经验回放机制,对于经验池中的样本,根据经验重要性赋予不同的优先级,样本优先级越大则其被采样到的概率就越高,即希望越重要的经验使用次数越多,从而增加学习效率。文献[7]提出根据经验样本的时序差分误差(temporal-difference)的不同,赋予每个样本不同的优先概率,误差值越高,表明模型评估的差异越大,越需要训练,重要性越大。文献[8]不仅考虑时序拆分误差,还引入了Q值作为划分标准。文献[9]采用了回合平均奖励作为优先级进行样本选取。可见优先经验回放机制中对经验样本的划分方法并不统一,一般与具体领域有关。
本文从提高大众麻将AI训练样本利用率角度出发,通过改进强化学习算法中样本利用方法,以便提升麻将AI的训练速度。
1 大众麻将游戏术语及规则
麻将是中国古代发明的一种不完全信息博弈游戏,在中国各地区都十分流行,不同地区有着不同的玩法。本文针对2021年中国计算机博弈锦标赛中大众麻将[10-11]进行研究,大众麻将游戏基本术语及规则如下:
玩家:大众麻将游戏由4名玩家组成。
牌库:牌的总张数。大众麻将分为条、筒、万三门,共计108张。
牌墙:开局发完初始手牌后,剩下的牌为牌墙,共55张。
局面:某位玩家在某一个时刻可以观察到的所有信息。
条:条子牌共有9种,由序数牌一条至九条组成,每一种都有4张,共有36张。
筒:筒子牌共有9种,由序数牌一筒至九筒组成,每一种都有4张,共有36张。
万:万字牌共有9种,由序数牌一万至九万组成,每一种都有4张,共有36张。
顺子:指同一花色中,顺序相连的3张牌,如“一万二万三万”。
刻子:指同一花色中,3张相同的牌,如“一万一万一万”。
对子:指同一花色中,2张相同的牌,如“一万一万”。
摸牌:玩家从牌墙中摸1张牌。
出牌:玩家从手牌中选择1张打出。
吃牌:当上家打出的1张牌和自己手牌中的2张牌构成顺子时,则可进行吃牌操作。
碰牌:其他玩家打出的1张牌和自己手牌中的2张牌相同,则可以进行碰牌操作。
明杠:指其他玩家打出的1张牌和自己手牌中的3张牌相同,则可以进行明杠操作。
暗杠:指自己手中有4张相同的牌,则可以进行暗杠操作。
补杠:指自己手牌中有1张和自己已经碰过的牌相同,则可以进行补杠操作。当牌墙中有剩余牌时玩家可以进行杠牌,玩家摸完牌墙最后1张牌不能杠牌。
和牌:分为点炮、自摸、和抢杠胡,点炮是指其他玩家打出某张牌结合我方的手牌组成和牌牌型,自摸是指自己摸牌后的牌型为和牌牌型,抢杠胡是指其他玩家补杠的某张牌结合我方手牌组成和牌牌型,和牌牌型通常是An+B的格式,A为顺子或刻子,B为对子,此外还包括七对(7个对子)和牌方式。
听牌:当玩家手牌打出某张牌后,还差1张牌就可以和牌时,此时的手牌是听牌状态。玩家可选择是否进行报听操作。报听后,虽然可以直接获得分数奖励,但是此后不可吃、碰操作,后续摸什么牌就打什么牌,直到场上胡的那张牌出现,才可进行和牌操作。且在不影响原来听的牌的情况下,当场上有合法的杠牌出现时,可以选择进行杠牌操作。
开局时4位玩家分东南西北入座,每人起手摸13张牌,庄(东风位置)玩家起手多摸1张牌,共计14张。之后由庄家位玩家开始按逆时针出牌操作,行牌过程中可进行摸牌、出牌、吃牌、碰牌、杠牌、报听和和牌操作。其中,吃牌、碰牌、杠牌、报听和和牌都可获得直接收益。且同一时刻可能会出现多种决策动作,各动作的优先级为:和牌>杠牌>碰牌>吃牌。当有玩家成功和牌或牌墙中的牌出完时,牌局结束,根据玩家动作以及和牌牌型的番种,统计各玩家的总分,麻将游戏番种如表1所示。

表1 麻将游戏番种
2 多重优先经验值的设计
由于大众麻将真人打牌数据有限,目前主要采用迁移学习[12-13]和深度强化学习的方法来进行研究,但在样本的使用上,存在两个问题:
1) 经验样本存在时序相关的特点,不符合独立同分布的假设,因此网络模型很难稳定地去学习。
2) 经验样本被利用一次后就被丢弃,样本利用率差。
为解决上述问题,将经验样本存入经验池,从经验池取出均匀采样用于训练的方法,但是这样做会导致经验样本浪费,效率也低。为了提高经验样本(Si,a,r,Si+1)的利用率,对重要的经验重复利用,本文综合考虑经验样本中局面Si的复杂程度D(Si)、时间差分误差δi、动作的即时奖励值ri三个因素。首先计算出经验样本中各个因素的优先值概率,然后通过对3个因素的概率值线性加权,计算出经验样本的总优先概率,概率值越大,被抽取的概率越大。本文通过提高重要样本的抽取概率,提高数据利用效率,加快网络的训练速度。
2.1 基于局面复杂程度的优先级
结合大众麻将游戏的特点,麻将游戏属于多人博弈游戏,游戏隐藏信息多,对手策略隐蔽,出牌不确定性程度高。由于距离和牌近的游戏局面往往比较容易取得胜利,局面相对简单,而距离和牌越远的游戏局面不确定性程度大,局面比较复杂。因此,本文在选择样本重要程度时考虑了不同时刻局面的复杂程度,并根据局面复杂程度给出优先级。
定义:麻将局面的复杂程度
一个局面的复杂程度为当前局面与游戏结束局面时的距离。即当前麻将局面下玩家替换若干手牌后可以和牌的最小值。
某个局面Si的复杂程度D(Si)计算。本文除了考虑计算4个搭子加1个对子的所有基本和牌牌型外,还考虑了七对这种特殊牌型,计算方法如式(1)所示。
D(Si)=min(D1(Si),D2(Si))
(1)
其中:D1(Si)表示计算4个搭子加1个对子的基本和牌牌型,计算方法如式(2)所示。
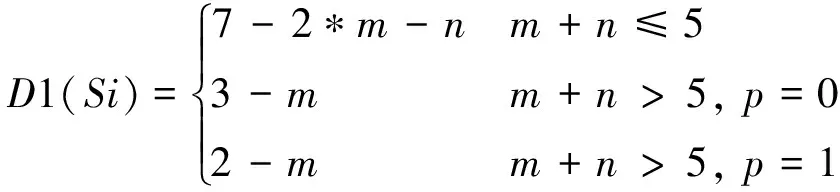
(2)
其中:m表示手牌中搭子(不相交的刻子数和顺子数);n表示手牌中不相交的搭子数(包括两面搭子、边张搭子、嵌张搭子和对子);p表示除去面子和搭子后手牌中是否还有一对子。
和牌不仅包括基本胡,还包括七对这种牌型,计算如式(3)所示。
D2(Si)=7-q
(3)
其中q表示当前局面的手牌中的对子数。
样本中局面复杂程度的优先概率计算首先通过式(1)先得到每个局面复杂程度大小D(Si),然后根据式(5)计算该时段局面复杂程度重要性值Mi,最后通过式(4)归一化得出样本局面复杂程度的选取概率PD。Mi表示样本i的复杂程度对应的数值大小。相关定义如下:
(4)
Mi=-e(D(Si)-φ)2+f
(5)
式(5)表示不同时刻下样本局面复杂程度大小,其中,e,φ,f为调节参数,e使得不同复杂程度优先级间隔平滑,f保证局面复杂程度对应的重要性值为正,φ使得AI在不同时间局面复杂度的优先级不同。起初φ=0,表示局面复杂程度为0的经验样本概率最大;随着游戏局数的增加,φ逐渐增大,局面复杂程度位于(0,φ)之间值的重要性逐渐变小;局面复杂程度最高为7,所以值位于(φ,7)的样本重要性逐渐增大,表明随着学习的时间增加,学到的局面复杂程度越来越大。
2.2 基于立即回报的优先级
在麻将游戏对局时刻t,对于状态St做出了动作a,并转移到下一个状态St+1时,会获得的立即回报为r。回报的绝对值大的样本往往反应映AI动作过好或者过坏,重要程度较高。因此,在选择样本重要程度时考虑动作的立即回报。立即回报选择概率如式(6)所示。

(6)
其中:i表示为经验样本中即时奖励的下标;ε是一个很小的常数,防止即时奖励为0的经验被抽取到的概率为0。
2.3 基于时间差分误差的优先级
在t时刻,状态为St,动作为at, AI的状态动作价值函数Q(St,at)与事先预估的状态动作价值函数Q(St+1,at+1)的差值称为时间差分误差。时间差分误差越大,表明AI对该局面动作选取越差,越需要学习更新。因此,在选择样本重要程度时考虑了样本时序差分误差。时序差分选择概率如式(7)—(9)所示。
δt=r+λQ(St+1,at+1)-Q(St,at)
(7)
pi=|δi|+ε
(8)

(9)
其中:λ为衰减率;ε是一个很小的常数,防止时序差分误差为0的经验被抽取到的概率为0。
2.4 样本多重优先级的计算方法
综合考虑局面的复杂程度、动作即时奖励以及时间差分误差,采用线性加权的方式计算样本总优先概率值,多重优先级计算方法如式(10)(11)所示。
(10)
(11)
其中:PTD(i),PR(i),PD(i)分别表示第i条经验样本的时序差分误差、奖励、复杂程度概率;a∈[0,1],b∈[0,1],c∈[0,1]为三者的权重,它们的大小随时间的增加而减小。随着游戏对局的增加,AI对经验的学习越来越不依赖于这些优先经验,当对局数目增大时μj减小。
2.5 降低学习率方法
提出的多重优先级回放方法改变了经验的抽样方式,但是它引入了偏差,不利于神经网络的训练。为此,通过使用重要性抽样(importing sample)对高概率样本降低学习率,以防止过拟合。
重要性采样权重如式(12)所示:
(12)
其中β∈ [0,1],网络刚开始训练时,β设置较小,随着网络训练β值逐渐增加至1。
2.6 优先级计算优化方法
相比于随机经验回放,优先经验回放在计算经验样本的优先级上需要额外的时间。所以,本文在经验样本优先级的计算以及经验样本的抽取上进行了时间优化。主要方法包括:
1)当一条新经验样本覆盖经验库时,需要重新计算经验库中每条经验样本的优先级,此时经验库中总局面复杂程度、总即时奖励以及总时序差分误差不必重新累加,优化方法如式(13)所示,其中W表示经验库中局面复杂程度、即时奖励或时序差分误差:
W总=W总+W移入-W移除
(13)
2) 当计算出个样本的总优先级值时,常用做法是对样本排序后按概率进行抽取,这种做法的平均时间复杂度为nlog2(n),本文通过构建sum-tree进行经验样本的抽取,时间复杂度为log2(n),如图1所示。

图1 sum-tree示意图
叶子节点表示经验库中样本的总优先级值,父节点为子节点之和,构建sum-tree时,当叶子节点不为2n时,用0节点补至2n,自下而上构建整棵树。节点旁红色数字为节点标号,叶子结点下面是他们各自对应的数值区间,叶子结点数值越大(优先级越高)其区间长度就越大,因此从0~11中均匀抽样一个数据落到这个区间内的概率也就越大,这就是按照优先级进行抽样的原理,具体抽样过程如下:
a) 给定0~根节点范围随机数s将根结点作为父亲结点,遍历其子节点;
b) 如果左子节点大于s,将左子节点作为父亲结点,遍历其子节点;
c) 如果左子结点数值小于s,将s减去左子结点的数值,选择右子结点作为父亲结点,遍历其子节点;
d) 直到遍历的叶子结点,该叶子结点的数值就是优先级,下标对应的数值下标,可以从经验库中找到对应的数值。
例如,图1给出随机数8.5,选择节点0作为父节点。8.5与节点1比较,8小于8.5,得到结果0.5,将节点2作为父节点, 0.5与节点5比较,0.5小于1,选择节点5,所以抽取节点5代表的经验样本。
3 基于多重优先经验值的大众麻将博弈算法实现
强化学习就是一个智能体(Agent)在状态(State)采取行动(Action)获得奖励(Reward)与环境(Environment)发生交互并更新的自身循环过程。
对于大众麻将游戏而言,要训练的AI可以看作一个智能体,博弈信息可以看作是环境状态,吃、碰、杠、听、胡、弃牌可以看作是行动,是否获胜,以及获胜的番种可以看作为奖励。博弈过程会随着智能体根据博弈信息做出策略,而转移到下一个状态,并获得一定奖励。麻将是一个四人博弈游戏,在一个智能体做完动作后,需要等其余3名玩家做出回应后才能使得环境状态进行转移。因此,本文将其他3个玩家设置为环境一部分。采用DDQN(double deep Q-learning)方法结合优先经验回放进行麻将AI训练。由于麻将数据离散,需要对麻将牌面进行表示,以供神经网络的输入,牌面表示如图2所示。训练流程如图3所示,其中红色虚线框中多重经验回放机制部分是本文重难点研究的内容。算法主要流程见算法1所示。
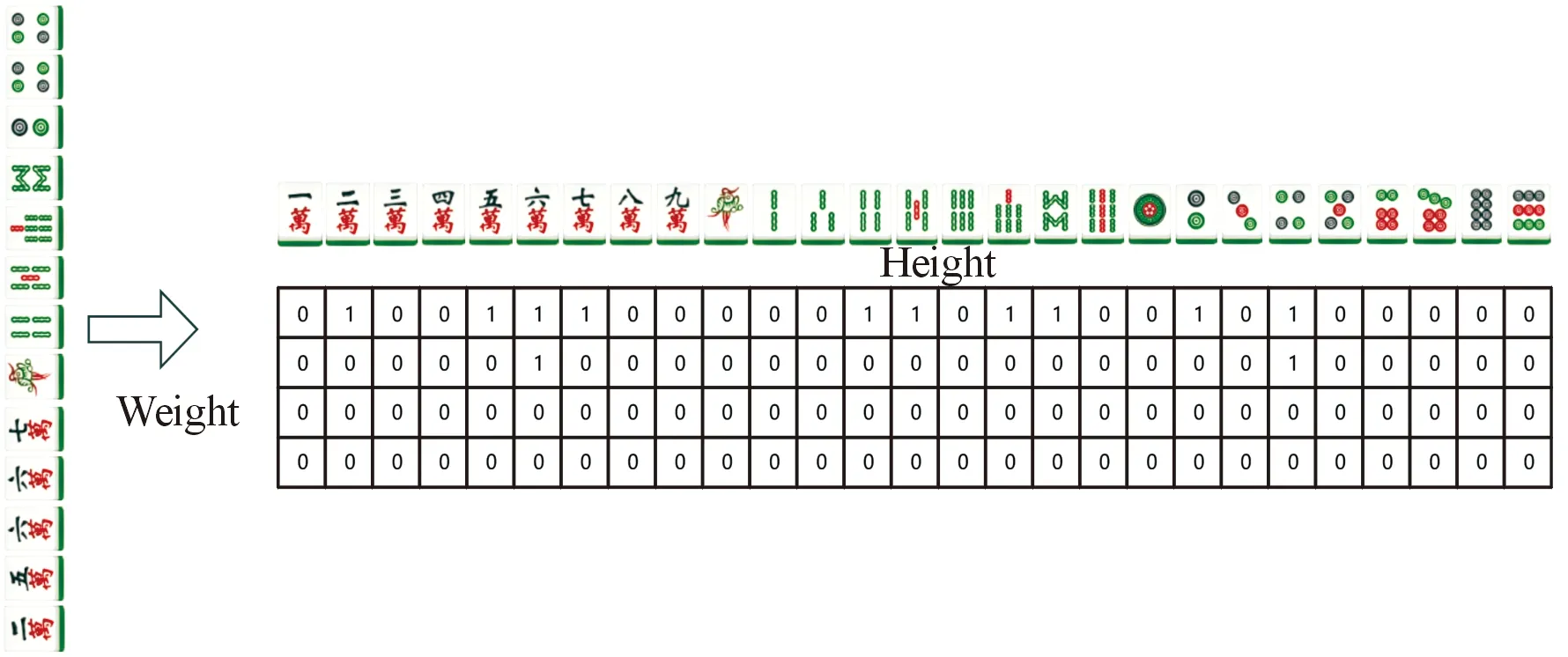
图2 牌面表示示意图

图3 DDQN算法训练流程框图
算法1:MPER-DDQN
1 输入:minibatch大小为k学习率为α,折扣系数γ,回放周期为K,存储数据大小为N,对局轮数M,单局对局时间T,探索率ε
2 输出:预测网络Q参数ε

4 for episode = 1 toMdo
5 fort= 1 toTdo
观察初始状态S0, 生成随机数n,n∈[0,1];
6 ifn<ε
选择随机动作at
7 else
at=maxaQ*(St,a;θ)
8 end
9 得到该动作奖励rt,以及下一状态St+1,并将经验样本(St,at,rt,St+1)存储在经验库H中;
10 forj= 1 toNdo
11 令yj=
//a为动作集,t′为时间步
12 计算δj=yj-Q(St′-at′);
13 计算P(j)D,P(j)r,P(j)TD;
14 计算优先级
15 iftmodK== 0 then
//间隔K步回放一次
fori= 1 tokdo
损失函数Loss:
计算样本的重要性权重ωj;
计算权重Δ←Δ+ωj·δj▽θ(St″,at″)
16 end for
17 更新预测网络参数θ←θ+α·Δ
18 更新有先经验权重系数μi=μi*μ
19 一段时间θ-←θ;
20 end if
21 end for
22 end for
23end for
在训练过程中,DDQN使用预测网络计算下一个状态下的对应各个打牌动作的Q值,并记录其下标,然后使用目标网络计算下一个状态里面的对应各个打牌动作,将预测网络预测的打牌动作索引对应的Q值作为目标Q值,避免了选取预测网络最大Q值的过程,从而一定程度上避免了对当前牌局下,对某个打牌动作过高Q值估计的问题,提高了训练的稳定性。Double DQN与DQN相同的是他们都有被称之为预测网络与目标网络的两个网络,只是在实作过程中,标签的计算过程做了修正,如式(14)。

(14)
yj表示模型训练时得到的Q值。如果当前一轮游戏结束,则rj值为最终Q值;否则,Q值不仅包含即时奖励rj,也包含预测网络对下一牌局状态预测的最大Q值。
与深度学习不同的是,DDQN输出的不再是预测出牌的概率,而是对于当前状态下每个动作的Q值,选取Q值最大的动作进行执行,进而利用eval网络得到最大Q值打牌策略的下标,然后利用target网络计算下一状态下执行该动作的实际Q值,进而计算当前局面下,执行该打牌动作后的收益,与预估收益的均方误差,作为DDQN的损失函数为:
(15)
4 实验平台搭建及实验结果
4.1 实验平台的搭建
在对智能体交互的环境进行搭建的文献中,OpenAI的gym[14]以及RLcard[15]给出了很好的范例,因此,本文借鉴其对智能体环境的搭建方式,并结合大众游戏自身的特点,建立一套大众麻将自博弈环境。其自博弈流程如下:
算法2大众麻将自博弈流程
1 输入:初始化玩家手牌hand,庄家位置dealer,该回合玩家p
2 输出:博弈结果
3p= 庄家;
4 while True do
5 ifp已经听牌 then
6 ifp和牌合法
7 直接胡
8 else ifp杠牌合法 then
9 获取p的动作内容
10 else
11 打出刚摸得牌
12 end if
13 else
14 验证p动作action合法性;
15 if action == 和牌 then
16 游戏结束计算得分
17 else if action == 杠牌 then
18 if 补杠 then
19 if 抢杠胡(判定动作是否合法)then
20 游戏结束
21 end if
22 end if
23 else if action == 弃牌 or 听牌 then
24 获取可行动作玩家动作;
25 判定优先级
26 Continue;
27 if 剩余牌数目大于0 then
28 摸一张(吃碰后不能摸);
29 else
30 游戏结束
31 end if
32 end if
33end if
4.2 实验结果与分析
在2080Ti服务器进行实验。实验的软件环境配置为:Windows 10,python 3.7,pytorch 1.4等,实验超参数如表2所示。

表2 超参数设置
为了验证本文方法的有效性,将提出的多重优先经验回放大众麻将程序 MPER-DDQN与基于随机经验回放麻将程序ER-DDQN各自博弈8万局,设置的对手麻将AI均为采用深度学习编写的2020年亚军程序[16]。由于麻将游戏对局初始手牌不同,每局游戏累计回报差异较大,故统计了每百轮平均奖励作为AI对局中的表现。实验过程中2个麻将AI程序对局中获得的累计回报如图4所示,横坐标为AI对局轮数,纵坐标为对局中获得的累计奖励。AI对局消耗的时间如图5所示,其中横坐标表现对局时间,纵坐标为对局所用时间。

图4 2种方法AI对局中累计回报
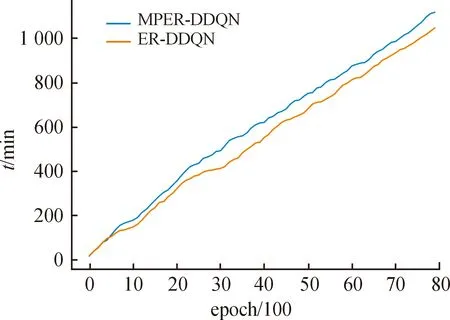
图5 2种方法AI对局中消耗的时间
从图4中可以看出,采用本文多重优先经验回放的方法AI在39 000轮对局可以达到收敛,而随机经验回放则大约需要61 000局。从图5可以看出,优先经验回放方法在8万个对局中总用时高于随机经验回放,分析其原因为计算优先级需要花费额外的时间。从实验数据得出,优先经验回放对局39 000轮收敛大约需要615 min,而随机经验回放则需要794 min。由此得出,本文所提出的方法将麻将AI的训练速度上提升了22.5%。
5 结论
通过分析麻将游戏的特点,提出了多重优先经验回放机制,给出了麻将游戏局面复杂程度的定义,通过时序差分误差、奖励以及局面复杂程度3个标准对经验样本优先值进行计算,并在笔者搭建的麻将自博弈平台进行对比实验。与传统的随机经验回放算法相比,麻将AI训练速度与稳定性大幅度提升。下一步,将在改进模型训练速度的基础上研究将麻将AI决策水平进一步提高。
——以中国、新加坡教材的三角形问题为例

