应用留数定理求解几道《美国数学月刊》的反常积分问题
范铭灿
(惠州学院 数学与统计学院,广东 惠州 516007)
柯西留数定理把计算周线积分的整体问题转化为计算各个孤立奇点处留数的局部问题。 基于该定理可以解决较复杂的一些反常积分,其技巧在于将其化归为周线积分。 经典的复变函数教材中,常见的反常积分类型包括有理三角函数型有 理 分 式 型或者多值函数型等[1-2]。然而许多反常积分并不总是以这些形式出现,例如《美国数学月刊》2021 年第8 期刊登的意大利R.auraso 提出的问题12274[3]、2021 年第9 期刊登的意大利P.Perfetti 提出的问题12281[4]、 2022 年第4 期刊登的沙特阿拉伯S.Stewart 提出的问题12317[5]、022 年第6 期刊登的爱尔兰F.Holland 提出的问题2332[6]、2022 年第7 期刊登的中国I.Mezo 提出的问题12338[7]尚未有正式参考解答。本文将结合换元法、分部积分法及含参量积分求导法将这几道复杂反常积分转化为常见类型,并应用留数定理给出解答,同时总结这类反常积分的计算技巧。将用到的引理陈述如下:
引理1(小圆弧引理[1])设函数 ( )f z 沿圆弧Cr: z - a = r eiθ(θ1≤ θ ≤ θ2,r 充分小)上连续,且z - a ) · f ( z )= λ于 Cr上一致成立,则
引理2(大圆弧引理[1])设函数 ( )f z 沿圆弧CR: z = R eiθ( θ1≤ θ ≤ θ2,R 充分大)上连续,且· f ( z )= λ于 CR上一致成立,则
引理3(若尔当引理[1])设函数 ( )f z 沿圆弧CR: z = R eiθ( θ1≤ θ ≤ θ2,R 充分大)上连续,且f ( z ) = 0于 CR上一致成立,则
问题12317[5]: 证明

与Tauraso[8]利用欧拉余元公式的解答方法不同,我们应用留数定理给出一种新的做法。
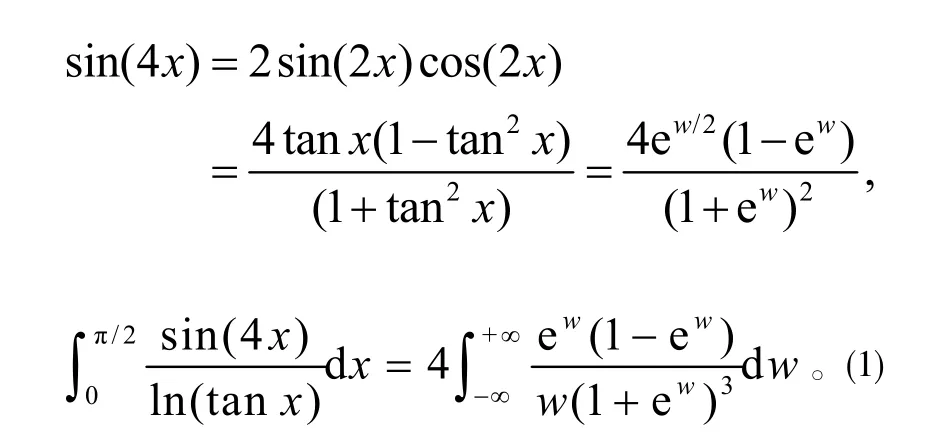
为了简化计算,应用分部积分法,得到


图1
注意到 1 + e(2k+1)πi= 0,k 为任意整数,得知函数f ( z )在闭曲线C 内具有一阶极点 zk= (2 k+ 1)πi ,k = 0,1,2, … ,N 。 应用留数定理,得到

令δ → 0+,N →+∞, 得到
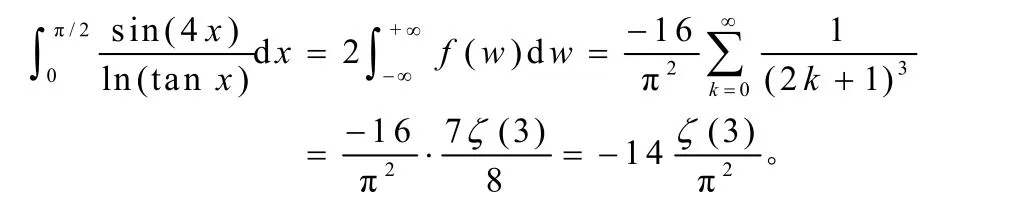
注1:这里利用换元法将瑕积分化为无穷积分(见公式(1)),方便构造闭曲线积分路径。积分的被积函数分母为ex的多项式与x 的多项式的乘积,易于求解孤立奇点。但是注意到式(1)中被积函数具有三阶极点,如果直接应用留数定理计算会比较复杂。这里利用分部积分法,降低了极点的阶数,从而使得函数的留数计算较为简便。另外,分部积分得到的新积分形式依然满足小圆弧和大圆弧引理,从而可以应用留数定理。
类似问题12317 的证明方法,可以证明问题12332。
问题12332[6]: 证明
证明 利用换元法,令x t=- ,则有
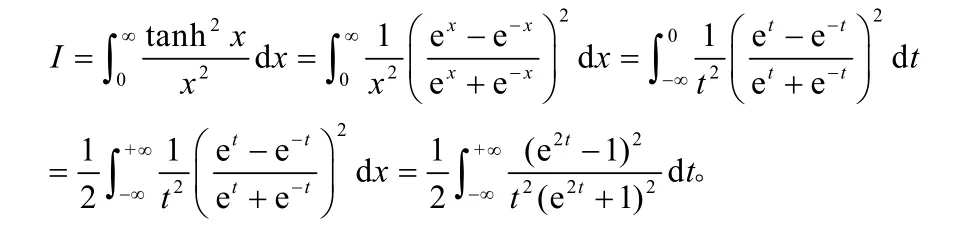
进一步利用换元法,令2t w= ,则有

类似问题12317 的证明过程,考虑函数

依然沿图1 所示的闭曲线路径C 的积分,得到

令δ → 0+,N →+∞, 可得
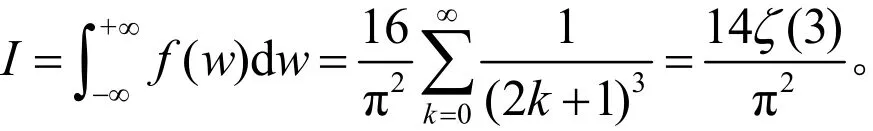
问题12281[4]: 计算积分
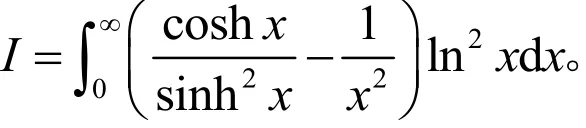
与Tauraso[8]利用Laplace 变换的解答方法不同,我们应用留数定理给出一种新的做法。
解 利用分部积分法化简原积分I ,得到

令 f ( z ) = g ( z ) · ln z ,其中

是偶函数。考虑函数 (f)z 沿图2 所示的闭曲线路径C 的积分。 利用洛必达法则, 易求得故由小圆弧和大圆弧引理,得到

图2
注意到 e2kπi- 1 = 0,k 为任意整数,得知函数f ( z )在闭曲线C 内具有一阶极点 zk= kπi ,k = 1,2, … ,N 。由留数定理,得到

进一步令 x = weπi,得到
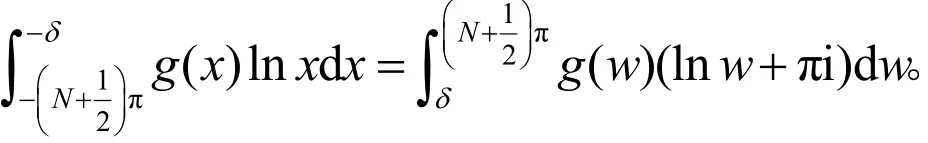
于是,


令 δ →0+,N →+∞,并对比公式(2)两端的实部部分,得到
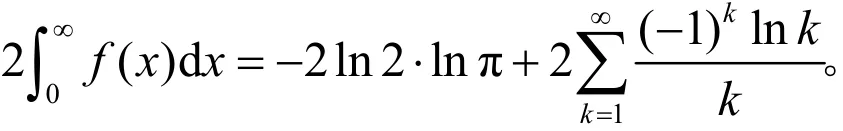
由于

下面将证明当n →∞时
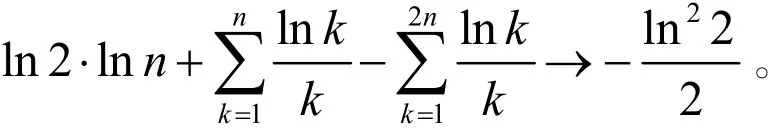
注意到
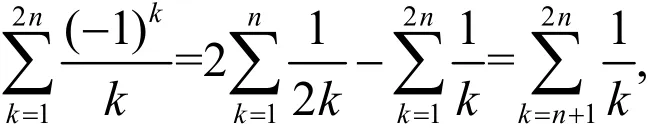
可得到
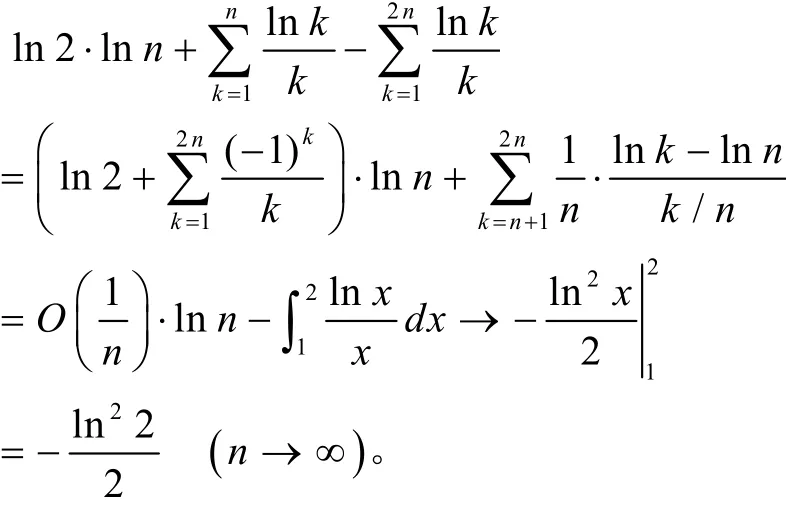
另外,由
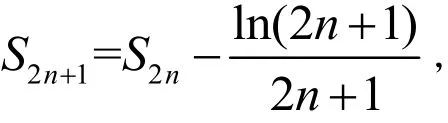
故积分

注3:使用分部积分法能够将原积分转化为类似多值函数型积分的形式。另外由于g ( z )为偶函数,该问题也可以考虑按照如图3 所示的闭曲线积分路径计算周线积分但是这样会使得留数的计算更麻烦。故选取恰当的周线积分形式非常必要。
问题12274[3]: 计算积分

与Tauraso[8]利用无穷级数的解答方法不同,我们结合换元法和留数定理给出一种较为简便的做法。
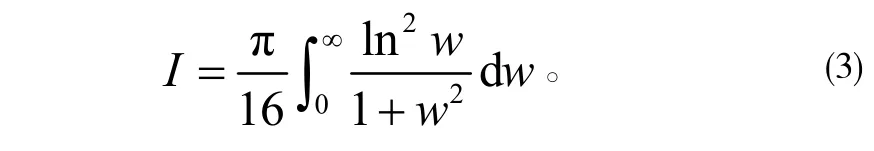
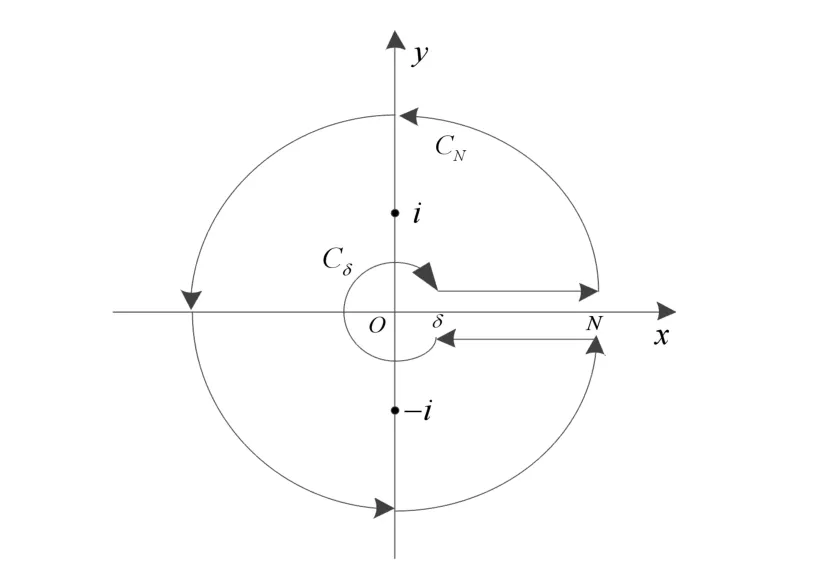
图3
显然 ( )f z 在闭曲线C 内只有一阶极点1iz =和2iz =- 。由留数定理,得到
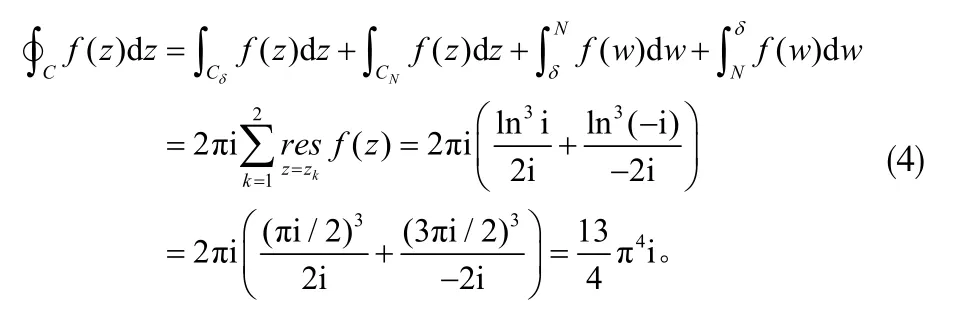
进一步令 w = xe2πi得到

令 δ →0+,N →+∞,并对比式(4)的两端,得
由留数定理,得到
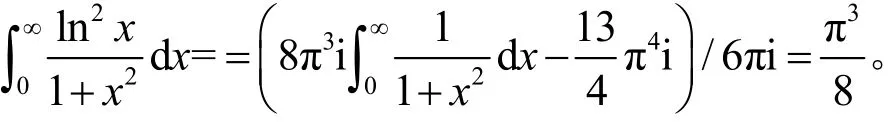
故积分
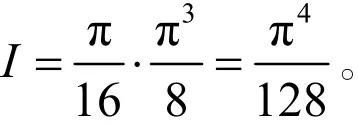
注4:此题也有其他简便的做法,例如可利用换元法, 令ln w x= ,使得公式(3)中被积函数的分母转化为ex的多项式与x 的多项式的乘积形式(可参考问题12317 的证明步骤)。而这里给出的做法是为了说明当反常积分为多值函数型积分形式且 g ( z )是偶函数时,考虑沿图3的周线积分将问题转化为计算积分以此递推,最后转化为计算积分从而使得留数的求解较为容易。
问题12338[7]: 证明
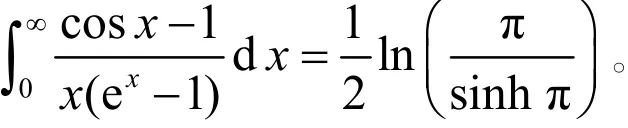
证明 定义含参量反常积分
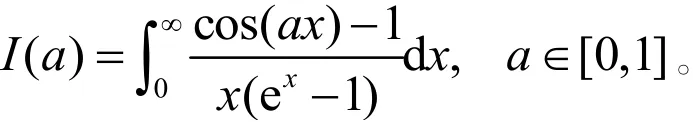
由于
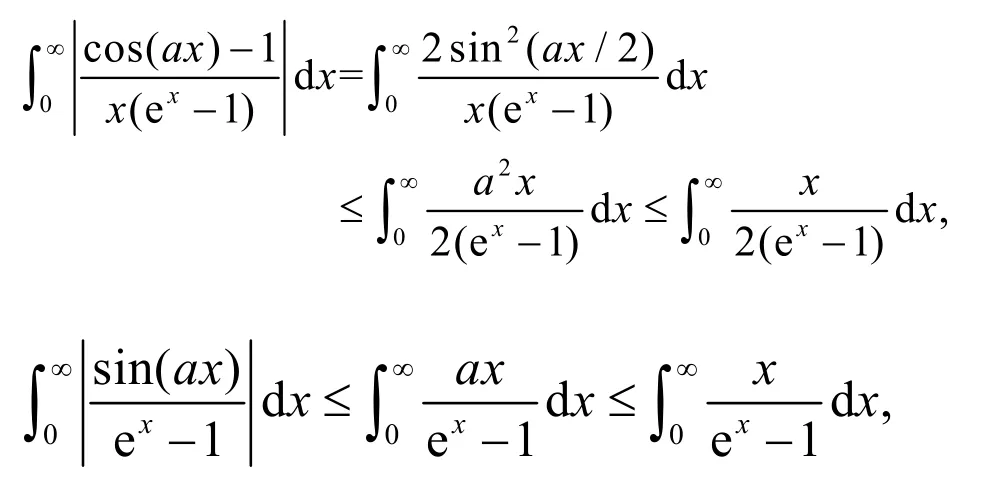

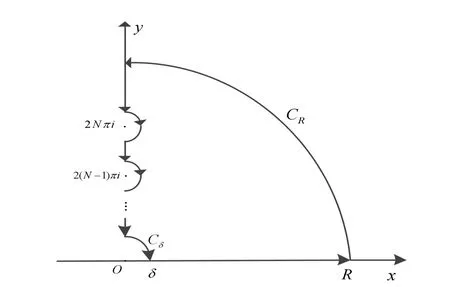
图4
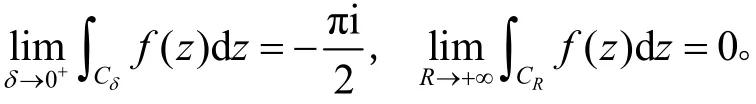
令 δ →0+,R →+∞,并应用小圆弧引理和留数定理,得到

由于
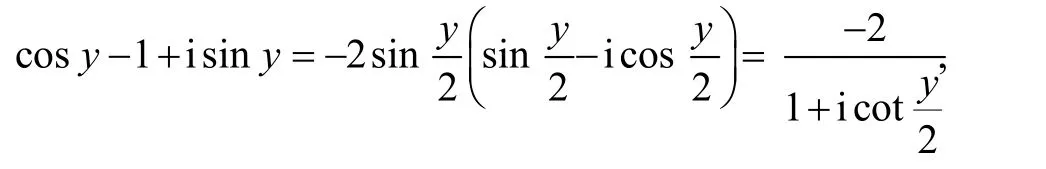
得到

对比公式(5)两端的虚部,得到

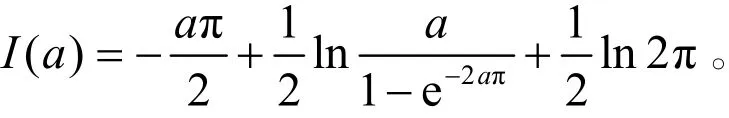
于是,

注5:这里利用含参量积分求导的方法,目的是将原积分转化为类似有理分式型的积分形式,从而方便使用若尔当引理和大小圆弧引理。之所以考虑沿虚轴的积分路径,是因为其相对于负实轴的积分路径,其对应的积分部分更容易计算虚部。

