非刚性点集匹配的机载下视图像目标定位方法

袁东华，赵化启，王宇春，程 岩，郭 浩，刘 琳，李国晶，刘晓敏

（1 佳木斯大学 信息电子技术学院，黑龙江 佳木斯 154000；2 佳木斯大学 材料科学与工程学院，黑龙江 佳木斯 154007）

0 引言

无人系统的感知与导航已经受到国内外广泛重视。美国发布了《无人系统综合路线图》，而中国科协将无人系统中高精度智能导航列为十大工程技术难题之一［1］。而基于视觉目标定位方法是无人机技术中研究的热点［2］。

本文研究的机载下视目标定位定义为给定目标图像（卫星图像）找到目标图像在参考图像（无人机图像）中的位置。目前基于深度学习的方法用于目标定位中，代表性的算法有Faster RCNN［3］、Strong-CNN［4］和CVM-Net［5］。相较于基于深度学习的目标定位方法，基于特征匹配的方法能够更好地完成智能定位任务［6］。传统的特征匹配方法是SIFT 特征匹配［7］，大量的改进算法用于自然图像的目标定位［8-11］已产生了好的效果。然而针对机载下视目标定位效果不好。微分同胚的非刚性点集匹配广泛用于医学图像处理，可解决大尺度形变问题［12-15］。综上所述，针对机载下视目标定位任务存在的问题本文提出有效方案，存在问题如下：

（1）传统点集匹配模型［7］具有固定自由度，无法解决大尺度形变的问题。

（2）现有的点集匹配算法［7］并未考虑噪声对变换模型的影响，当有异常点时得到的变换模型不准确。

（3）现有微分同胚大多为稠密微分同胚点集匹配方法［16］，无法用于机载下视目标定位中。

针对以上问题，本文提出以下创新：

（1）提出了新的非刚性变换的目标定位框架，创新在于随机采样微分同胚点集匹配的使用。

（2）现有微分同胚点集匹配通常是稠密的，本文创新提出关键点约束的微分同胚点集匹配用于机载下视目标定位。

（3）创新提出使用K-means 分类算法与随机采样结合的微分同胚点集匹配方法。

1 基于随机采样微分同胚点集匹配的目标定位方法

针对机载下视目标定位中的大尺度形变问题，本文提出了基于随机采样微分同胚点集匹配的目标定位方法，研究内容包括目标定位方法整体框架、图像关键点检测、特征匹配、随机采样微分同胚点集匹配方法以及目标定位相似性计算。

1.1 目标定位方法整体框架

本文提出了一种基于随机采样微分同胚点集匹配的目标定位方法，框架如图1 所示，该框架包括：关键点检测、特征点匹配、随机采样微分同胚点集匹配和目标定位相似性计算四个部分。给定目标图像和参考图像，首先利用SIFT 关键点检测方法确定目标图像和参考图像中的关键点集，通过随机K-D 树最近邻算法得到一致性关键点集，为了降低异常点对匹配性能的影响，如图1（b）所示，其中C11，C12，C13，C14表示每一个子集中的随机像素点，并构成C1像素点集合，使用微分同胚点集匹配方法拟合变换模型f1，迭代随机采样相同大小数据集，将数据集元素带入拟合变换模型，并统计符合模型的点集个数k1进行输出，使用同样方法确定点集C2至Cn，确定变换模型f2至fn，输出点集个数k2至kn，通过选择k1至kn中最大值确定最优变换模型，最后计算变换图像与参考图像的SSD 值确定目标定位结果。

图1 本文目标定位方法框架图Fig. 1 The framework of target localization method in this paper

1.2 关键点检测与特征点匹配

随机采样微分同胚点集匹配方法是基于关键点检测与特征点匹配基础之上，为了更好地确定目标图像和参考图像间的空间变换模型，本文使用SIFT算法检测目标图像和参考图像的关键点集。SIFT算法主要包括尺度空间极值检测、关键点的定位、确定特征点主方向和生成特征向量4 个步骤［7］：

（1）尺度空间极值检测：使用DOG（Difference of gaussian）算子构造尺度空间，并在尺度空间中搜寻极值点作为候选的特征点。

（2）关键点的定位：将候选的特征点定位到亚像素精度，并剔除不稳定的候选点。

（3）确定特征点主方向：利用特征点邻域像素的梯度分布特性确定每个特征点的主方向。

（4）生成特征向量：统计以特征点为中心的局部区域梯度，形成128 维梯度特征向量，并对其归一化。

为了获得一致性关键点集，本文使用随机K-D树最近邻算法计算特征点的相似性，随机K-D 树算法的主要思想是将K-D 树算法中的一棵树拓展为多棵树。首先，算法在数据集的所有维度上进行方差计算并按大小排序，然后在方差最大的前D个结果中随机选择一个维度来构建随机树。在搜索树时，首先用所有随机化的K-D 树构成一个优先队列，然后将此前一棵树的搜索变换成在多棵树上同时进行搜索，最后对结果进行排序获得最优相似性结果［14］，得到了一致性关键点集。

1.3 随机采样微分同胚点集匹配方法

微分同胚点集匹配属于非刚性点集匹配方法，与刚性点集匹配相比，非刚性点集匹配具有更多的自由度，这使得微分同胚更加适合具有大尺度形变的目标检测任务。然而在整个点集中直接使用微分同胚点集匹配方法会导致过拟合，使得定位结果不准确，因此本文引入K-means 聚类算法将一致性关键点集进行分类，并在多个子集上利用随机采样方法获得生成变换模型所需的子集，该方法有效地降低了异常点对目标定位性能的影响。以下内容针对微分同胚点集匹配和基于随机采样微分同胚点集匹配方法进行详细介绍。

1.3.1 基于微分同胚的点集匹配

给定二维图像的图像域是二维欧式空间，记为R2。目标图像X和参考图像Y的2 组对应特征点集，分别为：｛xi∈Ω1｜i ＝1，2，…，n｝和｛yi∈Ω2｜i ＝1，2，…，n｝，其中Ω1⊆R2和Ω2⊆R2。微分同胚点集匹配是要找到一个变换g：Ω1→Ω2，满足g（xi）＝yi，∀i ＝1，2，…，n。

微分同胚点集匹配有2 个重要特性：光滑性和拓扑保持性［15］。分别阐释如下。

（1）光滑性：当变换g的所有偏导数都存在且是连续的，那么变换g：Ω1→Ω2具有光滑性。

（2）拓扑保持性：匹配时如果Ω1和Img（g）＝｛x2∈Ω2｜∃y1∈Ω1，x2＝g（y1）｝有相同的拓扑结构，那么变换g：Ω1→Ω2具有拓扑保持性。

由微分同胚的特性可知，不仅能使图像在变换前后的拓扑结构不发生变化，并且还保留了原有几何结构的光滑性。因此，该类模型能拟合较大程度的非刚体形变。

微分同胚变换的构造先使用时间依赖的速度矢量场s（t）和相关联流来构造微分同胚变换群；再通过再生核希尔伯特空间方法来生成速度矢量空间S；在速度矢量空间S的约束下，计算能量泛函E（s）的最优解，生成满足微分同胚非刚体变换的形变场［16］。

假设s：［0，1］｜→S为时间依赖的速度矢量场，用其来构造微分同胚变换时，速度矢量场s（t，·）须满足下列方程：

使用再生核希尔伯特空间方法来构建速度矢量场空间S是构建微分同胚变换群的核心步骤。根据Riesz 定理，必存在空间S中Kx使得对于所有s∈S均有：

其中，＜·，·＞是希尔伯特空间S上的内积，记（x），则Kx（y）＝K（x，y）为S上的再生核。根据矢量空间样条插值相关原理可知，在空间S中插值问题的最优解形式可表现为：

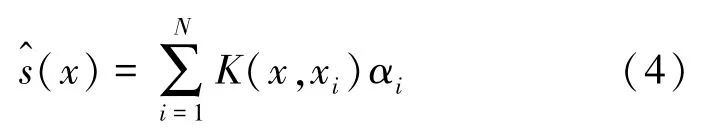
其中，α为再生核的系数矢量，这里根据希尔伯特空间S的范数定义可得：

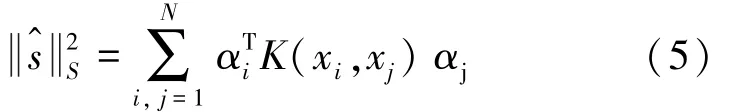
基于微分同胚非刚体变换的匹配的能量泛函如下：

1.3.2 基于随机采样微分同胚点集匹配方法

将微分同胚点集匹配方法直接用于一致性点集上会受到大量异常点的干扰，这导致微分同胚点集匹配结果很差，因此本文使用K-means 聚类方法有效地将一致性点集划分成若干子集，在多个子集上使用随机采样一致性算法来确定微分同胚变换模型，下面内容详细介绍了随机采样一致性算法、Kmeans 聚类方法以及基于K-means 随机采样微分同胚点集匹配方法。对此可做解析阐述如下。

（1）随机采样一致性算法。Fischler 等人［17］提出的随机采样一致性算法是一种通用的参数估计方法，用于处理数据中存在较大比例的异常值时，该方法具有一定的鲁棒性。假设可以被模型描述的数据称为内点（inliers），而无法适应模型的数据称为离群点（outliers）。随机采样一致性算法的思想是使用尽可能小的初始数据集得到初始解，并将可能的内点数据并入到内点集合中。不断重复，得到一个最大的内点集合，该集合对应的解为最佳解。

随机采样一致性算法的一般步骤如下：

输入数据集U，最大迭代次数N，判定为内点的阈值δ，内点数目阈值τ

输出内点集合U'

步骤1从U中随机选择确定模型参数所需最小的数据。

步骤2使用公式（1）求解模型参数。

步骤3从U中确定误差满足阈值δ的数据点，记为内点。

步骤4若内点与总点数的比值大于阈值τ，则用已找到的内点重新估计模型参数，输出内点集合U'并终止。

步骤5否则重复步骤1～4，最多不超过N次。

（2）K-means 聚类。K-means 算法是经典的基于划分的无监督聚类算法，能很好地将数据划分开，使得同一类中的数据具有较高的相似性，而不同的类之间的数据相似性较低，本文将一致性关键点集中目标图像的关键点集进行聚类，相应的一致性关键点集分成了若干个子集，接下来的微分同胚点集匹配方法将作用于若干子集上。

K-means 算法的核心思想如下：首先从数据集中随机选取p个初始聚类中心，计算剩余数据到每个初始聚类中心的欧式距离，选择距离最近的聚类中心形成p簇。接着，计算每个簇中数据的平均值来更新聚类中心并进行下一次迭代，直到聚类中心不再改变或达到预设的迭代次数才停止［18］。

（3）基于K-means 的随机采样微分同胚点集匹配。为了能够进一步降低一致性关键点集中的异常点对目标检测带来的影响，本文提出基于K-means聚类与微分同胚结合匹配方法，有效完成了目标检测任务。该方法首先通过K-means 聚类方法将一致性关键点集分成多个子集，在每个子集中随机采样关键点集，通过优化方法获得最佳微分同胚变换模型，基于K-means 的随机采样微分同胚点集匹配算法步骤具体如下。

输入一致性关键点集，最大迭代次数L，判定为内点的阈值σ，内点数目阈值T，相似性阈值S

输出微分同胚模型f

步骤1使用K-means 算法将一致性关键点集划分为m类。

步骤2分别从m类中随机采样，记为Ci1，Ci2，Ci3，Ci4，这里i ＝1，…，n，且合并为Ci（i ＝1，…，n）。

步骤3使用数据样本Ci（i ＝1，…，n）通过公式（1）和公式（6）拟合微分同胚模型fi（i ＝1，…，n）。

步骤4还未被采样的目标图像关键点通过fi（i ＝1，…，n）得到对应的映射点。

步骤5计算映射点与参考图像关键点之间的误差e，若e ＜δ，则判定为内点，否则为外点。

步骤6统计内点数目，记为ki（i ＝1，…，n）。

步骤7将ki与内点数目阈值T进行比较，若ki ＞T，输出对应的微分同胚变换模型fi，否则迭代次数加1，并重复步骤2～7。

步骤8若当前迭代次数为L、且ki ＜T，则输出ki中最大值对应的微分同胚模型fi。

1.4 目标定位相似性计算

记目标图像为I1，参考图像为I2。目标图像根据最优微分同胚模型进行变换得到变化后图像记为I3。变换后图像与参考图像之间相似性根据下面的公式进行计算：

其中，W和H分别为图像的宽和高；I3（x，y）为变换后图像在坐标（x，y）处的像素值；I2（x，y）为参考图像在坐标（x，y）的像素值。SSD值越小，说明相似性越高，当SSD小于设定阈值时，认为本次目标定位结果有效。

2 实验结果与分析

2.1 实验环境与实验数据

实验平台为：内存8 GB、处理器3.12 GHz、操作系统Win10 的PC。实验环境为：Matlab R2016b、Visual Studio 2015 和OpenCV 2.4.9。

实验数据为悉尼科技大学针对无人机地理定位问题发布的University-1652 数据集，该数据集以全球72 所大学的1 652 座建筑为目标位置，包含了卫星图像、无人机图像和每个位置的地面图像。University-1652 数据集具有多源、多视角特点，首先，该数据集的数据来源于3 个不同平台，分别是卫星、无人机和手机摄像头；其次，地面图像是从目标建筑的不同视角收集的，而无人机图像是从不同的距离和方向收集的［4］。本文实验选取University-1652 数据集的前101 类的卫星图像（每类1 张图片）及对应的101 类无人机图像（每类54 张图片），卫星图像和无人机图像大小均为512×512 像素。

2.2 评价指标

本文评价不同算法的优劣是通过比较相应的ROC曲线下的面积、即AUC值来判断的，AUC值越高代表算法性能越好。

ROC曲线的纵轴为真正例率，横轴为假正例率，两者定义如下：

其中，TP表示正类被预测为正类；FN表示正类被预测成负类；FP表示负类被预测成正类；TN表示负类被预测成负类。

假设ROC曲线是由有限个坐标为｛（x1，y1），（x2，y2），…，（xn，yn）｝ 的点按顺序相连得到，其中（x1＝0，xn ＝1），那么计算AUC值的公式可表示为：

2.3 基于微分同胚的非刚体变换模型与投影变换模型的比较

基于微分同胚的非刚体变换模型比投影变换模型具有更高的自由度，无论是刚体变换、还是非刚体变换，最小二乘法是最通用的模型拟合方法，本节使用最小二乘法对变换模型进行拟合，实验比较了微分同胚的变换模型和投影变换模型检测结果，结果如图2 所示。图2 中，曲线a）是基于最小二乘法的微分同胚点集匹配算法，曲线b）是SIFT＋最小二乘法投影变换算法。

图2 非刚性模型和刚性模型比较Fig. 2 Comparison of non-rigid and rigid models

图2 中，曲线a）对应算法的AUC值要远大于曲线b）对应算法的AUC值，因此基于微分同胚的非刚体变换模型比投影变换模型能更好地完成机载下视目标定位的任务。

2.4 随机采样微分同胚匹配实验结果与分析

本节使用随机采样一致性算法对基于微分同胚的非刚体模型和投影变换模型进行拟合，并与在一致性关键点集上直接进行微分同胚模型拟合加以比较，实验结果如图3 所示。图3 中，曲线a）表示随机采样微分同胚算法，曲线b）表示SIFT＋随机采样投影变换算法，曲线c）表示微分同胚点集匹配算法。

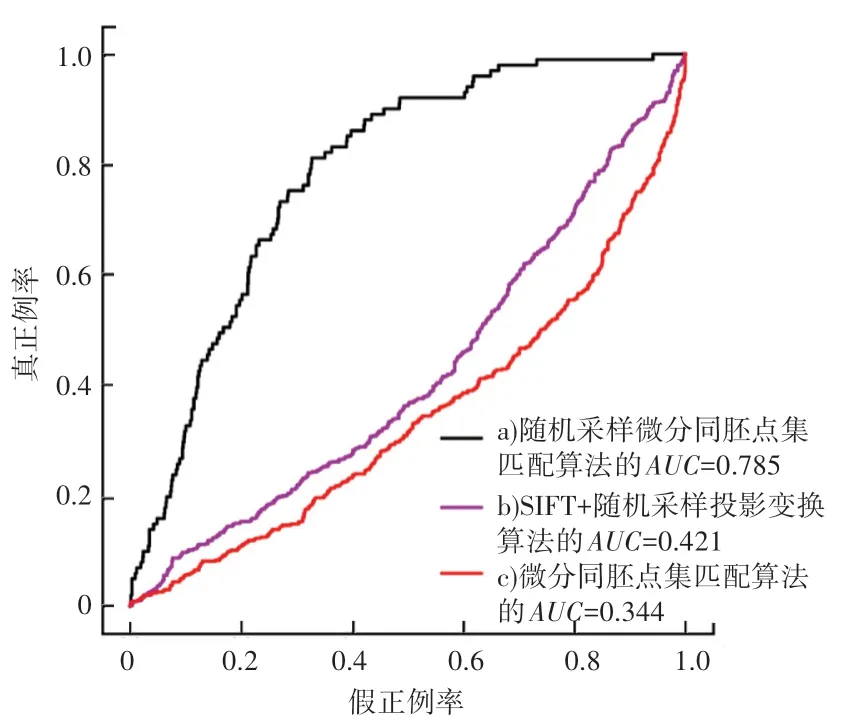
图3 随机采样微分同胚算法比较Fig. 3 Comparison of random sampling differential homozygous models

首先从图3 中曲线c）对应算法可以得出，直接在一致性关键点集上进行微分同胚模型拟合的结果是非常差的，因此需要对一致性关键点集进行处理。再比较图3 中曲线a）和曲线b）各自对应算法可得出，在一致性关键点集上使用随机采样一致性算法进行变换模型拟合效果更好，同时微分同胚比投影变换的随机采样算法要好。

2.5 K-means 聚类个数实验结果与分析

本节将讨论使用K-means 算法对一致性关键点集进行划分对随机采样微分同胚点集匹配算法的影响。

K 均值聚类是基于划分的聚类，该方法必须先指定聚簇个数，随后得到的聚类结果与初始选择的聚簇个数直接相关。虽然文献［16］指出最优的聚簇个数会落在的区间内（m为数据集大小），但经过实验发现一致性关键点集最大的聚簇个数为5。因此，本节实验分别将一致性关键点集划分为1（相当于未聚类）、2、3、4 和5 类，并在划分后的子集上使用随机采样微分同胚点集匹配算法进行实验对比，实验结果如图4 所示。

图4 不同聚簇个数的影响Fig. 4 Effect of different number of clusters

由图4 可看到，曲线b）、曲线c）、曲线d）和曲线e）各自对应算法的AUC值均大于曲线a）对应算法的AUC值，且曲线d）对应算法的AUC值最大。因此，使用K-means 算法对一致性关键点集进行划分，在每一个稀疏化子集中使用随机采样方法能有效提高随机采样微分同胚点集匹配算法的性能，且将一致性关键点集划分为4 类时，对随机采样微分同胚点集匹配算法性能的提升最大。

2.6 现有目标定位算法比较

为了证明本文提出的目标定位算法的优势，本节将建议的算法与DEMONS 算法、LDDMM 算法、CVM-NET 算法、Faster RCNN 算法、Strong-CNN 算法和基于SIFT 的随机采样投影变换算法进行比较，其对比结果如图5 所示。

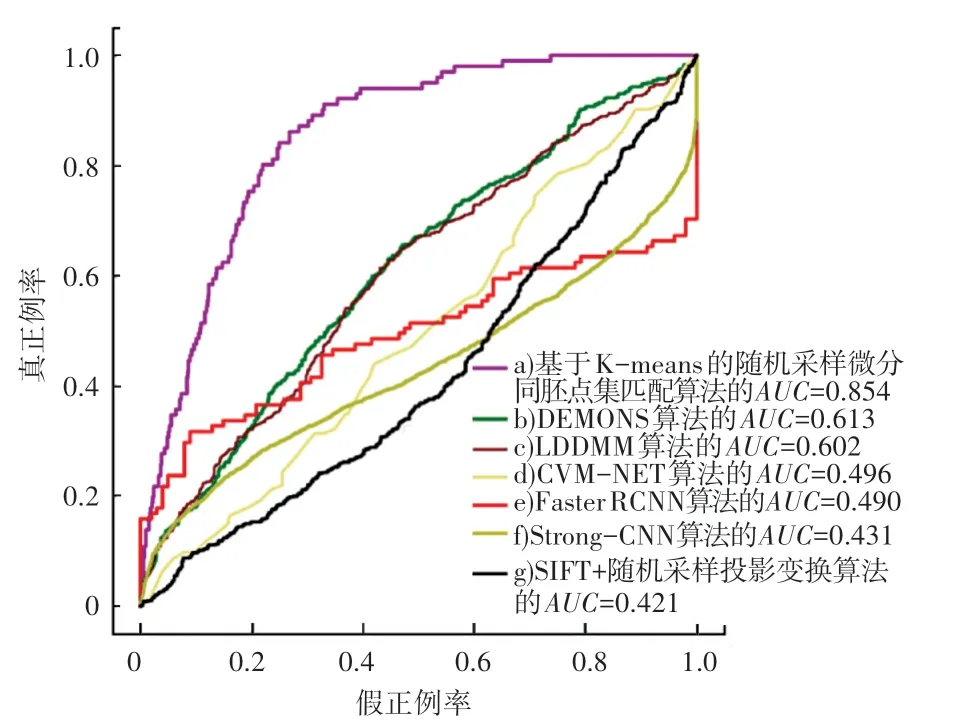
图5 主流算法比较Fig. 5 Comparison of mainstream algorithms

传统SIFT 投影变换方法具有最小的准确率；常用的几种目标定位方法CVM-NET、Faster RCNN 和Strong-CNN 算法优于SIFT 算法，但是准确率没有达到最高。从实验看出，基于微分同胚的目标定位方法DEMONS 和LDDMM 算法在本文任务中具有较大优势。而本文建议的方法比现有的微分同胚的目标定位方法准确率提高了24%，实验结果表明本文提出的方法可有效地用于机载下视目标定位任务中。

上述算法的时间效率对比见表1。由表1 可知，本文算法检测一幅图像所需的时间要高于DEMONS 算法、LDDMM 算法、Faster RCNN 算法、Strong-CNN 算法、CVM-NET 算法以及SIFT＋随机采样投影变换算法。因此需要进一步改进来提高算法的检测速度，这也是后续拟将探讨研究的方向。

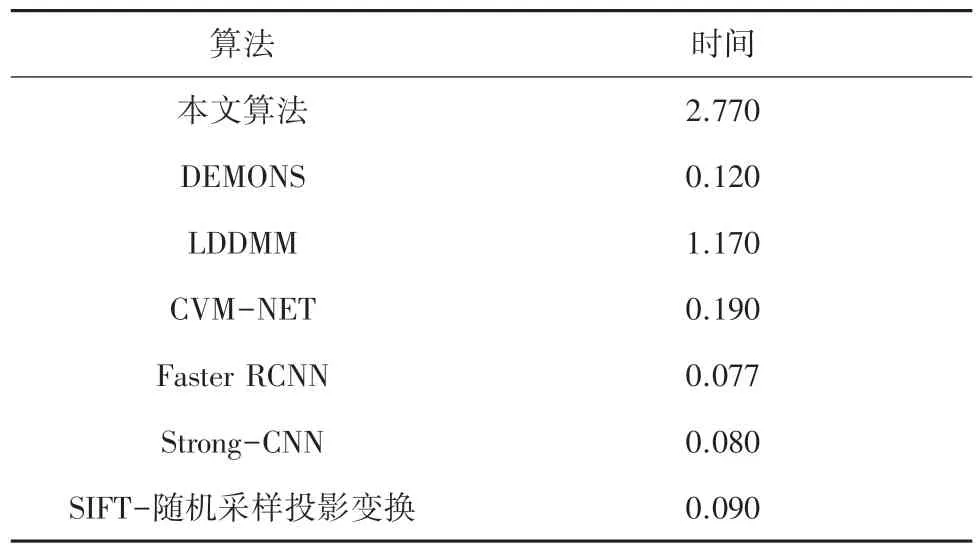
表1 时间效率对比Tab.1 Time efficiency comparison min

3 结束语

针对机载下视目标定位中目标图像与参考图像之间存在的大尺度形变问题，本文提出了一种非刚性点集匹配的目标定位方法。首先，使用SIFT 算法提取目标图像和参考图像的关键点，随机K-D 树最近邻算法用于获得一致性关键点集。然后，Kmeans 分类方法将一致性关键点集划分成多个子集，并在多个子集上使用随机采样微分同胚点集匹配方法优化空间变换模型。最后，通过SSD大小来确定最优目标位置。实验结果表明，本文提出方法的准确率比现有方法高24%，能够有效地完成机载下视目标定位任务。但是由于基于微分同胚的非刚性点集匹配自由度较大，因此算法运行时间较长，如何提高算法的实时性是下一步需要研究的内容。