核心素养下的设计思维在初中数学教学中的应用

李鹏程

核心素养的提出，是我国对人才质量标准的重新定位，也是教育发展赋予改革的新使命。如何在基础教育传统课程的课堂教学中，实现学生核心素养的提升，成为当下基础教育改革创新亟须解决的问题。

一、设计思维的概念及其在我国教育中的探究

核心素养以培养全面发展的人为核心，其综合表现为六大素养，即人文底蕴、健康生活、学会学习、科学精神、责任担当、实践创新。而设计思维的概念，最早由赫伯特·S·西蒙在1969年出版的《人工科学》一书中提出，他认为设计思维的核心是创造性，能够确定明确的目的，能够分析问题产生的背景，进而催生出理解问题、解决问题的想法，通过头脑风暴，能够对解决方案进行优化与深化。由此可见，设计思维与核心素养的教育理念高度一致，设计思维必然会作为重要的核心能力之一被导入基础教育阶段。

近几年，我国提出了关于设计思维的政策导向，教育部门积极提倡基础教育阶段的教育改革，促进基础教育阶段开展关于创客、STEAM、情景教学等新的教学模式，更新教学理念、教学内容和教学方式，积极进行课程改革。另外，教师需要利用信息技术积极建设众创空间的教学模式，形成具有地方和学校特色的校本课程，积极探究STEAM等新的教育模式。

目前，设计思维在基础教育阶段的应用还处于起步和探究阶段，很多地方的中小学联合社会力量开展了很多有益的尝试。2016年，同济大学的设计创意学院与黄埔区联合创办了“上海同济黄埔设计创意中学”;2018年，北京大学附属中学、南京外国语中学相继开设了设计思维课程。

随着国家和政府对教育投入的不断增加，教育改革也在积极开展，各学段中的传统课程是设计思维培养和发展学生核心素养的很好切入点，中小学已有的课程配置的师资、活动空间与传统的实验教学经验为开展核心素养下的设计思维与学科融合的教学探究提供了可能，实现了教学理念、教育思想的质的变化，适应了新时期提升中学生核心素养的需要。

二、设计思维有助于数学核心素养的实现

数学学科对培养学生形成正确价值观、必备品格和关键能力的贡献，就是发展学生的数学核心素养。在发展数学核心素养的过程中，学生逐渐学会了用数学的眼光观察世界，用数学的思维审视世界。

数学核心素养对理解数学学科的本质，设计数学教学都有着重要的意义和价值。核心素养的提出强调了教育改革的必要性，不仅要尝试改革目前基础教育阶段教育教学的内容和形式，还要注重培养学生的思维，引导学生学会解决问题，进而形成设计思维意识。

三、设计思维可以依托于实际问题来呈现

將设计思维渗透到初中数学教学中，教师需要依托实际问题来实现。例如，在教学六年级上册制作一个尽可能大的无盖长方体容器时，教师可以创设情境，提出问题：“如图1所示，用一张正方形的纸怎样才能制成一个无盖的长方形容器？”

图1

教师要给学生充足的思考时间，让学生展开头脑风暴，思考可不可以利用圆规、量角器等工具，可不可以将剪去的纸再贴上后折叠等问题。此时，教师不要过早介入学生的分析探讨过程，而应等学生表达完自己的想法后，再告知学生课上讨论的情况是：“在正方形的四个角上各剪去一个同样大小的小正方形，且剪下来的小正方形不再使用。”

然后，教师请学生观察自己制作的盒子，并思考被剪去的四个小正方形的边长与折成的长方体盒子的高之间有什么样的数量关系。

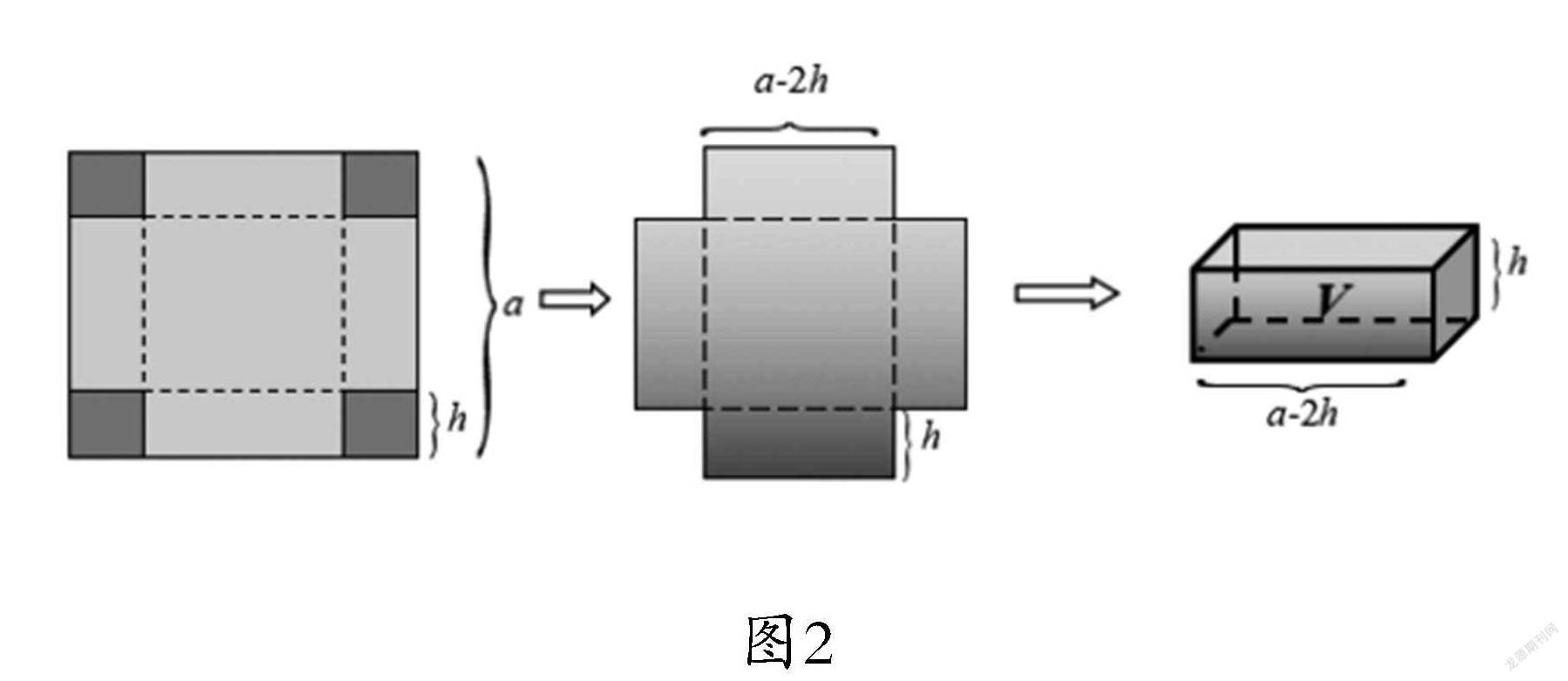
学生亲自经历画、剪、折等一系列操作活动，真实探究折成的无盖长方体纸盒的长、宽、高，以及原来纸片的边长与剪去的四个小正方形的边长之间的数量关系，如图2所示，为下一步求得长方体的体积扫清了障碍，认识到剪下的小正方形的边长对长方体的体积有较大的影响。

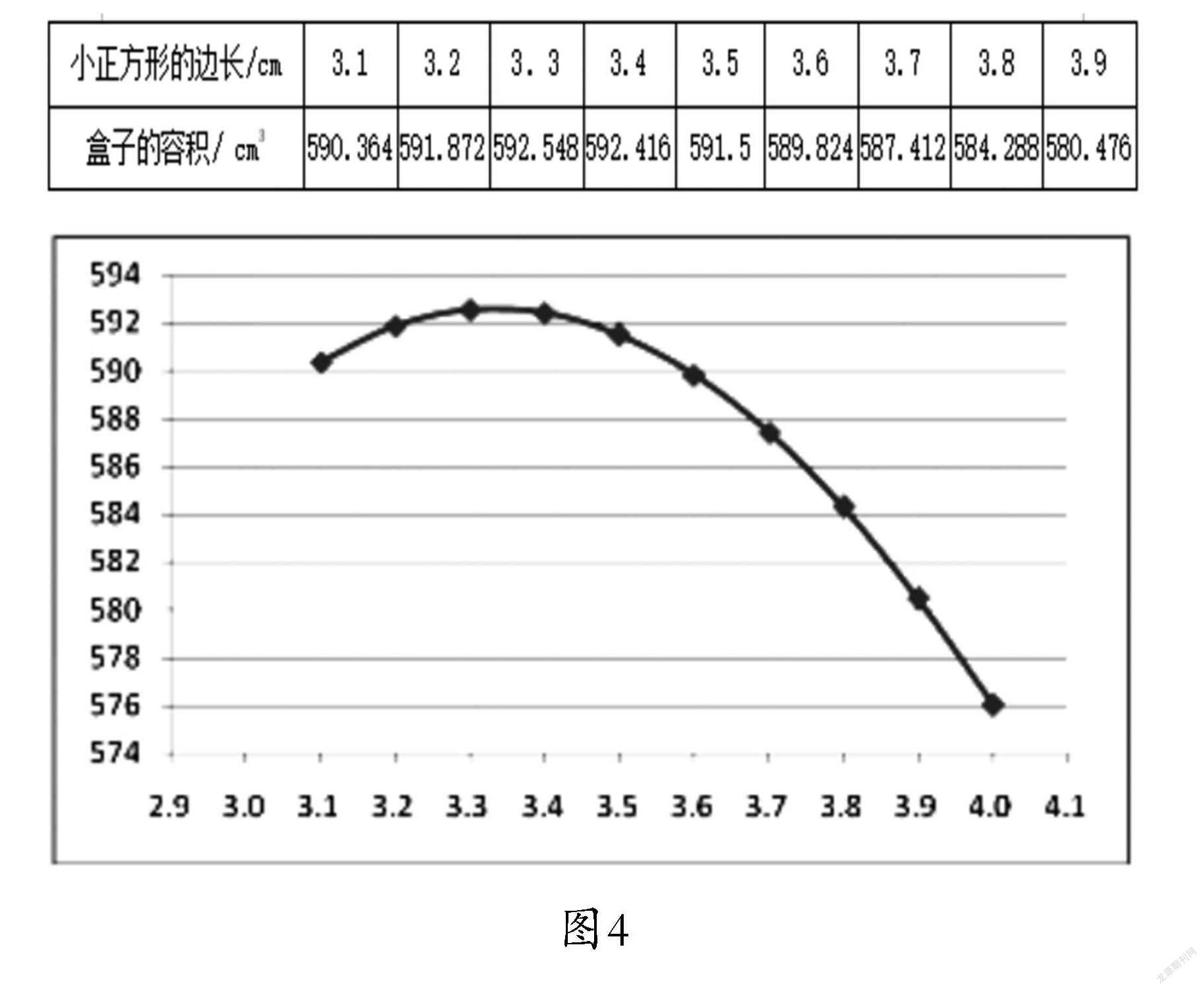
之后，教师又通过一系列问题引导学生思考如何剪、如何折，让学生经历试验、想象、猜测的过程，通过独立思考或小组合作交流感悟得到如下结论：随着剪去的小正方形的边长的增大，所折无盖长方体容器的容积是由小变大，再由大变小。通过小组分工合作的方式完成课本提供的表格，借助计算器制作统计表和统计图，如图3所示，进而得出正确的结论。

接着，教师又提出问题：“改变剪去的小正方形的边长，你能制作出容积更大的无盖长方体容器吗？”通过对问题的层层改编来引导学生思维层层递进，在不断改变的问题情境中激活创新思维。教师通过问题串式的提问，引导学生反思刚刚经历的数学活动，进一步明确了感悟研究方法、研究方向，也发现小正方形的边长取的都是整数值，进而引发思考：“如果剪去的小正方形的边长不都取整数值，那么相关的结论会不会有什么变化呢？”如图4，得出正确的结论。

教师可以让学生经历试验、想象、猜测的过程，感悟正确的探究方向，通过小组合作，探究当h取什么值时，V的值最大，归纳出结论，体会分割逼近的思想，掌握探究学习的方法，让学生经历“从实际问题抽象出数学问题—建立数学模型—综合应用已有的知识解决问题”的过程，体验建立模型、解决问题的方法，并在此过程中发展思维。

四、设计思维通过问题的解决过程得到不断强化

设计思维离不开真实的问题情境，从情境中发现问题到构思解决问题的方向和思路，到最终形成具体的解决问题的方案，设计思维体现出设计者如何针对问题进行有效合理的分析，如何综合使用已有的知识储备，以及如何在多种方案中权衡利弊，最终实现方案的最优化设计。

以九年级上册设计遮阳篷为例，首先，教师通过一个简单的实际问题，让学生体会具体问题模型化的过程，通过此问题使学生明确：实际应用问题和一般的数学问题不同，需要根据题意画出图形，分析已知条件与未知条件，然后再根据所学知识寻求解决问题的策略。

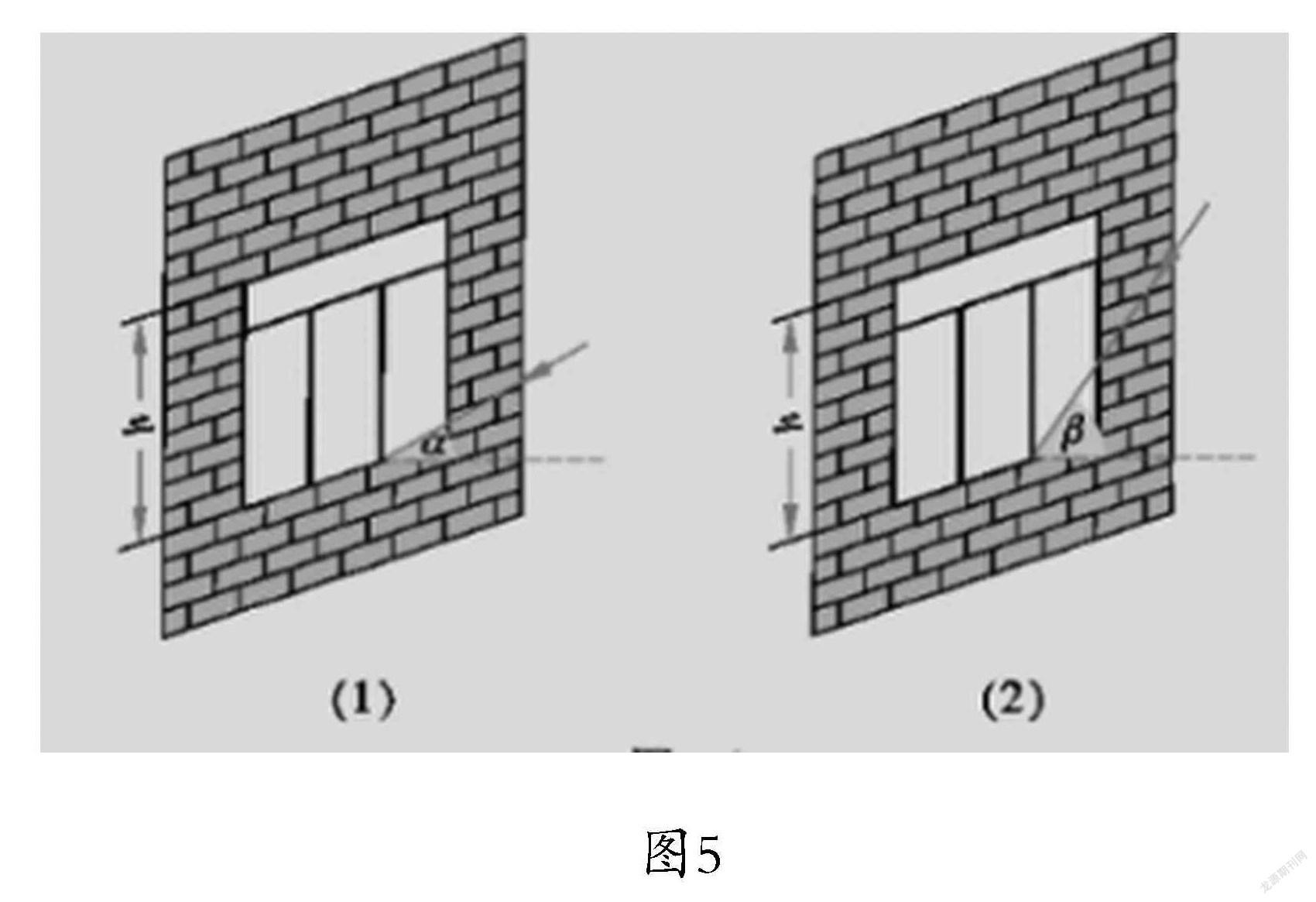
教师提问：“如图5所示，如果我们要做一个既能遮挡夏天炎热的太阳光，又能让冬天的阳关进入室内，固定的遮阳篷，那么遮阳篷应如何设计？

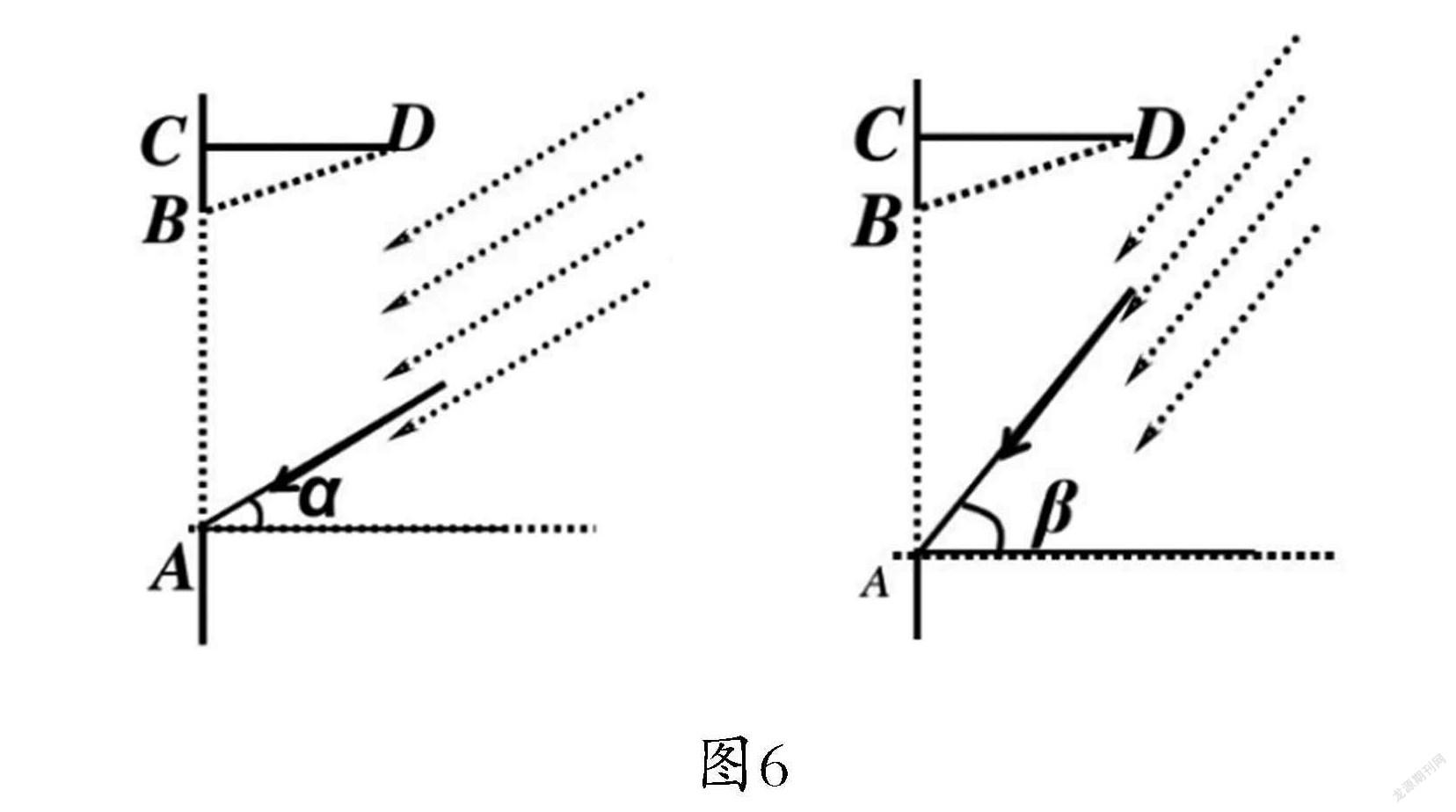
教师问：“如图6所示，冬天，我们都喜欢沐浴阳光，将太阳的光线与地面的夹角记为α，要想使太阳光刚好全部透过窗户射入室内，设计的遮阳篷BCD应该具备什么条件？ BC，CD唯一吗？（留给学生足够的思考时间）”

教师继续问：“夏天的阳光尽可能地留在外面，当太阳光与地平面的夹角为β时，要想使太阳光刚好不射入室内，此时的遮阳篷BCD又该如何设计呢？BC唯一吗？CD呢？”

教师接着问：“要同时满足上面两个条件，在冬天能最大限度地使太阳光照射到室内，而且在夏天又能保证最大限度地遮挡阳光，那么遮阳篷BCD又该如何设计呢？此时的BC唯一吗？CD唯一吗？请你尝试用含h、α、β的代数式来分别表示BC和CD。”

在设计遮阳篷时，学生往往要考虑夏日与冬日的不同需求。有了前面的铺垫，教师此时提出问题，学生就有解决问题的思路。当学生推导出最后结果时，教师可以展示生活中的遮阳篷图片，让学生对照自己的设计，判断是否符合实际。通过对比，学生很容易发现自己的设计过于理想化，在现实中遮阳篷还要考虑到防雨功能、安装防盗网等问题。随着不同问题的呈现，学生需要不断修改最初的设计方案，所以教师可以让学生进行组间的交流，或者让学生课下研究，留有充分思考与交流的时间。

五、结语

综上所述，设计思维的融入可以引导学生建立现实问题和已有知识储备之间的关系，锻炼学生的设计思维，提升解决现实问题的能力。因此，教师要将设计思维融入初中数学学科教学，运用具有启发性和创造性的教学模式，从而更好地培养中学生核心素养。

（作者单位：济宁市第十五中学）