线性代数课程思政元素的挖掘及教学改革实践

武慧虹 钱淑渠 黄宝勤 张汗洁 金文琼

(安顺学院数学与计算机科学学院, 贵州 安顺 561000)

2016年12月习近平总书记在全国高校思想政治工作会议上指出：要坚持把立德树人作为中心环节，把思想政治工作贯穿教育教学全过程，实现全程育人、全方位育人，努力开创我国高等教育事业发展新局面[1]。2020年6月，为深入贯彻落实习近平总书记关于教育的重要论述和全国教育大会精神，把思想政治教育贯穿人才培养体系，教育部印发《高等学校课程思政建设指导纲要》 (教高〔2020〕3号)的通知[2]。通知要求：建设高水平人才培养体系，必须抓好课程思政建设，解决好专业教育和思政教育“两张皮”问题。纲要强调：理学类专业课程，要注重科学思维方法的训练和科学伦理的教育，培养学生探索未知、追求真理、勇攀科学高峰的责任感和使命感；工学类专业课程，要注重强化学生工程伦理教育，培养学生精益求精的大国工匠精神，激发学生科技报国的家国情怀和使命担当。

线性代数作为理工科重要的基础课程，课堂教学如何融入课程思政是当前高等教育教学改革的重要课题。本文以《线性代数》这一具有代表性的大学数学基础课程为对象，探讨教师如何在课堂教学内容设计中融入思政元素，推动线性代数课程教学改革、落实立德树人根本任务，使相关专业基础课程与思想政治理论课同向同行，形成协同效应，同时也为其他类课程思政元素挖掘提供一定的思路和方法。通过课堂实施验证了线性代数课程融入思政教育对增强学生学习数学的积极性、调动课堂学习气氛等具有重要的作用，通过试验对比，表明课程思政融入课堂教学能有效提高学生对该课程的学习效果。

1 线性代数课程融入思政的研究现状

近年来，为贯彻落实专业课程在思政教育中的功能，专家学者积极开展专业课程思政建设，产生了许多优秀案例。如上海部分高校推出“中国道路”“大国方略”等一系列课程思政示范课[3]，这些成果的应用改变了专业课程任课教师的传统教育观念，创新了课程思政建设的新方法。但由于主要集中于人文社科类范畴，与在理工类课程中如何落实思政育人的方法有一定的差距[4]。因此，迫切需要探索理工类专业课程思政建设的新路径，当前具有影响的理论和实践成果较少。许淑琴等[5]认为课程思政建设的关键在于教师，她指出，教师首先要坚持立德树人理念，深入挖掘所授课程中蕴含的思政元素，围绕德智体美劳全面发展的理念开展课堂思政教学设计。文献[6]认为线性代数课程思政可围绕课程的发展历史和教学的知识点挖掘蕴含的思政元素，加强学生的世界观、人生观和价值观的教育，发挥线性代数在思政教育中的价值引领作用。文献[7]从线性代数课程思政的教学目标出发，提出个人修养、文化自信、勇于创新等五个思政教学融入点，设计了推动线性代数发展的数学家，教学知识点和课外拓展三个方面的思政案例。文献[8]从历史文化、美学思想和金融应用方面挖掘线性代数的思政素材。何薇等[9]围绕学习、文化、实践“三课堂”挖掘线性代数的知识点、数学史料、应用实例的思政素材，以激发学生爱国情怀和报效祖国的人生观和价值观。杨威等[10]分析了在大学工科线性代数课程教学中开展思政教育的优势与不足，从线性代数知识点出发，结合“特殊数字、数学发展史、科学家故事、马克思主义哲学思想”等深度挖掘思政元素，并给出了16个思政元素设计案例，为线性代数课程思政建设提供了很好的借鉴。王涛[11]等分析了开展线性代数课程思政建设的必要性，围绕行列式定义、线性方程组消元和向量空间概念设计思政教育案例，并强调了线性代数课程思政建设对落实理工类学生立德树人教育具有重要的意义。孙晓青等[12]认为开展线性代数思政教育是教学手段多元化的一种手段，有助于提高学生学习数学的兴趣，建立和谐、融洽的教学环境。

综上可知，诸多专家学者积极探索线性代数知识与思政的融合思路，产生了许多值得借鉴的思想方法，然而理工类课程思政建设尚未建立统一的模板，可复制、可推广的成功案例较少，线性代数课程思政元素仍未得到充分挖掘，在理工农医及经管类专业的线性代数课程教学中尚未得到广泛推广，对理工类学生的影响力还不够。本文结合已有的研究成果，对线性代数课程的思政元素进一步挖掘，基于该课程的教学内容，从知识点出发构建课程思政教学案例，激发学生学习数学的兴趣，有效在专业基础课教学中开展大学生的思想政治教育，进而在我校理工农及经管专业全面推广应用，着力将思政教育贯穿于线性代数课堂教学的主渠道，使线性代数课程与思政教育同向同行，形成协同效应，从而有效落实立德树人的根本任务。

2 线性代数课程思政元素的挖掘及教学改革

行列式和矩阵是线性代数课程中处理线性问题的重要工具，是研究线性方程组和变量的线性变换问题基础，贯穿于线性代数课程内容的各章节。本文重点围绕矩阵和行列式相关思政元素的挖掘和教学案例改革设计，从而为其他模块知识点思政元素的挖掘提供设计思路和方法。

2.1 由矩阵的定义挖掘思政元素

案例1. 定义矩阵加强红色教育。由于矩阵是由数字构成的数表，设计如下12个数字的数表

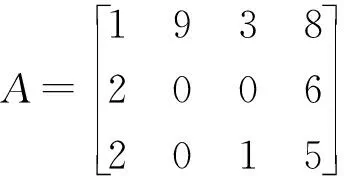
该数表的每行4个数字正是无产阶级革命家王若飞烈士经历的一个特别年份，1896是他的出生年，1922是他参与发起成立旅欧少年中国共产党之年，1946是他由重庆返回延安途中因飞机失事不幸遇难之年[13]。由1896、1922和1946这12个数字构成如下矩阵

本案例中给出王若飞烈士生平的重要时间节点，弘扬革命烈士的伟大精神，宣传教育学生铭记革命烈士王若飞，巧妙引出“红色安顺”。

案例2. 通过数字贯穿爱校教育及大学生使命感。安顺学院1938年成立于黔江师范学校，历经黔江师范学校、黔江中学、省立安顺师范学校、安顺师范高等专科学校等发展阶段，迄今已有80多年的历史。2006年经教育部批准，升格为本科层次。2015年安顺学院通过教育部普通高等学校本科教学工作合格评估。

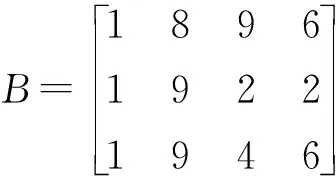
由学校成立、升本、通过合格评估的年份构成如下矩阵

让学生铭记学校的重要发展转折点，增强为校增光的使命感，铭记学习的发展史。

分析：案例1和2从数字出发，引出“革命传统”和“爱校意识”等思政元素，帮助大学生树立正确世界观、人生观和价值观，培养学生作为一名安顺人和安顺学院学子的责任感和使命感。

2.2 由行列式与矩阵概念引出思政元素

虽然形式上相类似，但其实质存在非常大的区别，通过分析实质，教会学生看问题要透过现象看本质，加深概念的理解，培养学生严谨的科学精神。

分析：矩阵A和行列式D虽然表示方法及形状极为相似，但其本质不同，矩阵A是一个数表，而行列式D是一个值。这就是说矩阵与行列式表面现象是相同，但其本质是不同，教会学生处理问题时要透过现象看本质，严谨治学作风。特别是当今社会之未有大变局，国家花费巨资将我们培养成为国之栋梁，毕业后有的学生选择了华为，攻克祖国芯片难题，为国排忧解难，而有的学生选择了google等国外公司，为追求个人利益透露甚至出卖国家技术机密，进行钱权交易，与未来国家接班人背道而驰，以此告诫学生，虽然我们的学生毕业后都找到了理想的工作，但其与初心和使命相违背，以此教育和引导学生毕业后“报效祖国，为国争光”的爱国情怀。

2.3 由单位矩阵的重要角色挖掘思政元素

案例4.单位矩阵存在如下性质 (1)AE=A； (2)EB=B；(3)B(E-A)=B-BA

由(1)～(3)等式看出，单位矩阵E可有可无，扮演着无关紧要的角色。但下列问题中单位矩阵E又发挥着重要的作用。

案例5.

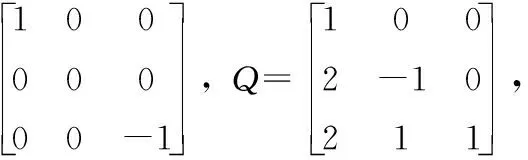
因为

所以Q是可逆矩阵，又因为AQ=QB⟹A=QBQ-1

所以

100个A

=QBQ-1Q)B(Q-)Q)B…(Q-1Q)BQ-1

=QB(E)B(E)B…(E)BQ-1=QB100Q-1

(1)

而

由此得

式(1)巧妙利用Q^(-1)Q=E的过度作用，将一个复杂的问题化繁为简，充分发挥E的重要角色，从而突破本问题的求解困难，对复杂的问题迎刃而解。

分析：案例4和5表明单位矩阵E在不同的场景发挥不同的作用，不需要的时候它会默默消失，需要的时候它会发挥顶天立地作用。引导学生要做单位矩阵式的人物，哪里需要就出现在哪里，不为功名利禄而学习，而是要在社会中发挥雷锋式、钱学森之精神，树立崇高的学习志向和科技报国的决心，树立积极的人生价值观，多为他人服务。

2.4 由矩阵初等变换折射思政教育

案例6. 矩阵的标准型是由一般矩阵经过有限次初等行变换，再经有限次初等列变换，最后成为标准型矩阵。标准型矩阵既美观、对称、简单，又体现原矩阵的很多性质。如矩阵

通过按行和按列的一系列初等变换，将一个不规则的、性质不清楚的矩阵化为标准型矩阵，转化过程中围绕标准型矩阵的目标经过多次反复的初等变换，要求学生必须保持科学的运算规则和严谨的转换思维，稍有不慎就不能得到正确的变换形式，经过反复多次精确计算后最终化为想要的标准型，达到理想目标。

分析：对标准型矩阵的转换和计算过程，引出要想成为一名标准(合格)的师范生如同标准型矩阵生成过程一样。刚开始从一名高中生进入大学时，没有人能知道自己将来适合做什么，能在哪些方面凸显出自己的内在价值，在大学阶段经历人格素养的教育，专业理论知识及技能的提高，最终成为标准的师范生(准人民教师形象)。由此激发学生人生奋斗的目标，体会成为合格人才的锤炼过程如下：

让学生体会到人需要经历各种能力的培养和提高，才能成为一个合格的人才，培养学生的数学核心价值观和价值取向。

3 教学实践

为了验证课程思政教学效果，2021-2022学年度第二学期在计算机科学与技术专业的(1)班(45人)和(2)班(48人) 线性代数课堂教学上进行试点。其中(1)班融入“课程思政”案例教学，(2)班采用一般的课堂教学，设置调查问卷题项如表1所示，所获结果统计情况如图1所示。

表1 调查问卷题项

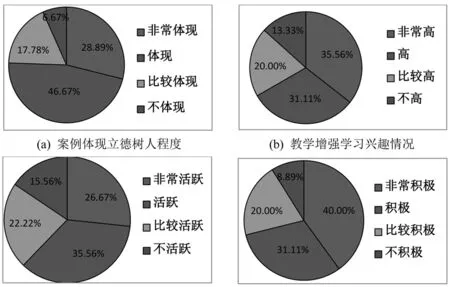
图1 调查结果统计饼状图

由图1的调查结果统计可以看出线性代数思政案例设计体现了立德树人根本任务，融入课程思政教育增强了学生的学习兴趣，调动了学生学习的积极性，增强了课堂教学的活跃性。对该试验班学生进行了访谈，很多学生表示原来害怕数学到现在喜欢数学，特别是对线性代数基础知识和基本方法记忆更深刻，概念更明确。

将(1)班和(2)班期末考试试卷成绩分析比较如图2所示。由测试结果表明，融合思政教育的(1)班在90-99分数段内占4.44%，而(2)班没有超过90分的成绩。在70-79、80-89和90-99三个分数段内，(1)班占比均超过(2)班，由此可见，融入思政元素后多数学生学习效果得到明显的提高，而(2)班学生中有突出的成绩较少，40-69分数段内学生数明显高于(1)班。

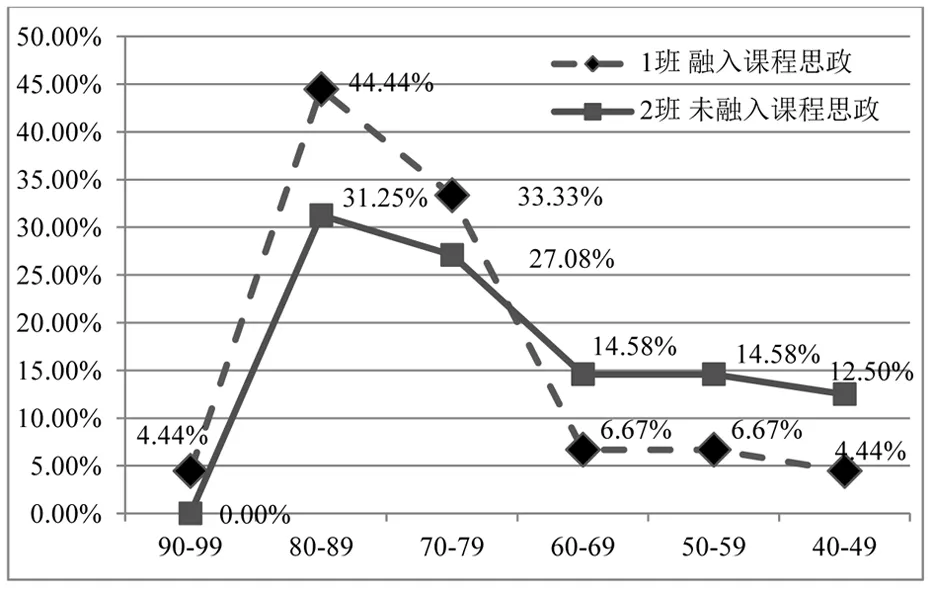
图2 融入课程思政的实践效果比较

4 总结

本文首先从国家政策分析了课程思政对人才培养的重要性，以线性代数课程为例，探讨了线性代数实施课程思政教育的优势，综述了国内外专家学者对线性代数课程思政建设的研究成果及成功案例，以线性代数课程中的矩阵、行列式和线性变换等知识点提出思政元素的挖掘策略和教学改革，结合这些知识点给出了6个课程思政教学案例设计，该研究结果对线性代数课程思政的设计方法提供一定的参考价值，同时也可对大学数学其他课程的设计提供一定的借鉴。通过对两个班级课堂教学实践，统计结果充分表明实施课程思政教学的班级取得明显的教学效果。本文对线性代数教学内容中线性方程组、向量及线性空间相关知识模块的课程思政元素的挖掘未进行讨论，这需要进一步深入探索，将在后期研究中继续呈现。