小学一年级儿童的非符号数量表征与数学成就

孙 霁 洪 梅 孙 沛

(1.安顺学院教育科学学院，贵州 安顺 561000；2.安顺经济技术开发区龙井小学，贵州 安顺 561000；3清华大学心理学系，北京 北京 100084)

数学是个体整个学习过程中的主要学习科目，也是科技教育相关学科(如物理、化学)的基础。2019年，科技部、教育部、中科院和自然科学基金委联合印发的《关于加强数学科学研究工作方案》(国科办基〔2019〕61号文件)明确提出“数学是自然科学的基础，也是重大技术创新发展的基础。数学实力往往影响着国家实力，几乎所有的重大发现都与数学的发展与进步相关”。从国家层面来看，经济合作暨发展组织(Organization for Economic Co-operation and Development，OECD)2010年提出如果将每个人的数学成就和科学能力提高半个标准差，那么整个国家的GDP将会提高0.87%。从个人层面来看，数学成就的高低直接关系到其未来的求学和就业，尤其是会影响个人未来是否会选择科学技术相关专业作为求学和就业目标[1]。但是数学学科的独特知识体系也让其成为个体最难学习的科目之一。如何有效培养个体的数学能力、提升学生的数学成就(即学生的数学测验得分)成为摆在心理学和教育学研究者面前的重要问题。小学阶段作为学生数学学科学习的起始阶段，也是其数学成就提升的关键时期。大量心理学和教育学研究从学校、家庭和个人等角度探讨了小学阶段学生数学成就的影响因素[2][3][4]。其中，备受关注的制约数学成就表现的个人因素之一是非符号数量表征(non-symbolic numerical representation)。已有研究发现非符号数量表征是个体数学成就的重要影响因素，但是同时也有研究者对个体非符号数量表征与数学成就间关系提出质疑[5]。目前对于二者的关系尚没有得出一致的结论[5]。因此，本研究拟以小学一年级儿童为对象，通过考察非符号数量表征、数学成就及其他相关控制变量，探索非符号数量表征与数学成就的关系。

近二三十年，非符号数量表征是数量认知和数学能力研究领域关注的重要因素[6][7]。非符号数量表征是指快速地、相对准确地估计物体数量的能力[8]，是人与动物共有的能力[9]。因为其对个体生存和发展具有重要作用，研究者也将其称为数量感知(number sense)[8]。关于非符号数量表征对个体数学成就具有重要影响的观点得到了以下三方面研究结果的支持。第一，大量研究发现，非符号数量表征与个体数学成就之间存在显著正相关[10][11][12]。例如，Wang等人[13]发现非符号数量表征能力较低的幼儿会有较差的数学表现。针对不同的年龄群体(如青少年、成年人)，非符号数量表征与数学成就间相关关系同样存在[14][15]。Halberda等人[14]发现5～11岁儿童的非符号数量表征与其不同数量测试成绩间呈显著正相关。这意味着，小学阶段儿童的非符号数量表征越好，其数学成就越好。第二，为了进一步验证非符号数量表征与数学成就间关系，研究者通过纵向研究设计发现了非符号数量表征对数学成就的预测作用。例如，2013年，Starr等人[16]研究发现，6个月大婴儿的非符号数量表征偏好与其3年后的数学测试得分有显著相关。这说明，非符号数量表征是后续数学表现的重要预测因素[10]。第三，最重要的是，还有研究者发现通过训练个体的非符号数量表征能力能够有效提升其数学成绩[17]。以上研究结果均有力地支持了非符号数量表征与数学成就间的关系。

然而也有研究对非符号数量表征与数学成就间关系提出质疑[5][18][19]。一些研究发现个体非符号数量表征与数学成就之间不存在相关[18]或只是弱相关[19]。例如，Soltesz等人[18]发现4-10岁儿童的非符号数量表征与计算能力测试成绩的相关关系不显著。另外，Caviola 等人[19]发现小学生的非符号数量表征与数学成绩之间只存在弱相关；相反，符号数量表征(symbolic numerical representation，即迅速、正确地加工数字的能力)和视空工作记忆(visuospatial working memory)能有效预测学生的数学成绩。为什么已有研究关于非符号数量表征与数学成就关系出现不一致结果？研究者认为可能有以下原因：第一，有研究者发现个体非符号数量表征与数学成就间相关关系的存在可能是有条件的[20][21]。例如，Gilmore等人[21]发现非符号数量表征与数学测试成绩间相关关系是源于非符号数量表征任务中抑制控制(inhibitory control)的作用。也就是说，当非符号数量表征任务同时考察被试的非符号数量表征与抑制控制时，被试的非符号数量表征任务得分才与数学测试成绩显著相关；当非符号数量表征任务只考察被试的非符号数量表征，不考察抑制控制时，被试的非符号数量表征任务得分与数学测试成绩无关。Fuhs和McNeil[20]研究也发现，当控制儿童的抑制控制能力得分后，儿童的非符号数量表征得分与数学成绩之间的相关就变得不显著。第二，有实证研究表明，个体非符号数量表征与数学成就之间可能存在中介变量[22]。例如，Guo 等人[22]发现个体非符号数量表征与数学测试成绩之间存在非符号-符号数量映射能力(numerical mapping ability，即个体将物体数量与相应数字对应起来的能力)这一中介变量。

综上所述，尽管当前关于儿童数学成就及其影响因素的研究很多，但仍缺乏一致的结论，尤其是个体非符号数量表征与数学成就的关系仍需实证证据。因此，本研究在以往研究基础上，以小学一年级儿童为被试，测量其非符号数量表征、数学成就及其他潜在的影响因素(包括符号数量表征、非符号-符号数量映射能力、视空工作记忆和抑制控制)，探索小学一年级儿童非符号数量表征与数学成就的关系，为小学生数量认知和数学成就研究领域相关理论提供实证依据，同时也为刚进入数学系统学习阶段的低年级小学生提供有针对性地促进数学学习、提升数学成就的方法和路径。

一、方法

(一)被试

研究选取安顺市某小学一年级23名学生作为被试，其中男生15人，女生8人，平均年龄6.68岁(SD = 0.63)。所有被试智力发育正常，无其他不良躯体疾病，视力或矫正视力正常。实验前，所有被试家长了解实验流程并提供知情同意书。被试完成实验的时间约为60～90分钟，因时间较长，为保证实验数据的质量和有效性，整个实验分为两次进行。实验后，每位被试均获得一份小礼物。

(二)实验材料与流程

本研究包括以下六个部分内容。

1. 非符号数量表征

采用 Halberda等人[23]提供的非符号数量表征比较任务(包含Panamath实验程序包)，由计算机呈现实验材料。每个试次中，电脑屏幕左右呈现两个方框，方框中分别是黄色圆点和蓝色圆点，圆点的数量在5～20个点范围内随机选择，呈现时间为200ms，要求被试判断：蓝色圆点的数量多还是黄色圆点的数量多。被试判断后进入下一试次。每位被试完成约8分钟实验后，实验程序包通过下列公式在线计算每位被试的韦伯系数(w)[23]：

其中，Pincorrect是被试反应的错误率，erfc是互补误差函数，n1和n2是黄点和蓝点的数量。计算1-w作为非符号数量表征得分。非符号数量表征得分范围为0～1，得分越高，非符号数量表征越好。

2.符号数量表征

采用 Batchelor等人[24]的符号数量比较任务，由计算机呈现实验材料。每个试次中，白色屏幕左右呈现两个黑色的阿拉伯数字，数字的数量范围为4～9，呈现时间为750ms，要求被试判断：左右两边的数字哪个更大。为了消除数量距离效应的影响，在一半试次中，两个数字的数量距离远，如4和9；在另一半试次中，两个数字的数量距离近，如8和9。每位被试完成40个试次后，计算其正确率，作为符号数量表征得分。符号数量表征得分范围为0～1，得分越高，符号数量表征越好。

3.非符号—符号数量映射能力

采用Mundy和Gilmore[25]的非符号-符号数量比较任务，由计算机呈现实验材料。每个试次中，白色屏幕上方呈现黑色圆点，下方左右两边呈现两个阿拉伯数字，圆点和数字的数量范围均为4～9，呈现时间为2000ms，要求被试判断：下方哪个数字的数量与上方圆点的数量是一致的。为了消除数量距离效应的影响，在一半试次中，圆点和正确数字的数量距离远，如4和9；在另一半试次中，圆点和正确数字的数量距离近，如8和9。每位被试完成40个试次后，计算其正确率，作为非符号-符号数量映射能力得分。非符号-符号数量映射能力得分范围为0～1，得分越高，非符号-符号数量映射能力越好。

4.视空工作记忆

采用Batchelor等人[24]的视觉搜索任务，实验材料为一个圆形托盘(直径为39cm)，11个不同颜色的纸杯(直径为6.5cm)，9张白色贴纸(2cm×3cm)和1张硬壳纸板(29cm×40cm)。实验开始前，主试随机将纸杯倒置摆放在托盘上，并告诉被试：“现在我们要去玩一个寻宝游戏。这是一些纸杯，它们都是不同的颜色。你能告诉我它们是什么颜色吗？”该问题是为了确认被试能够正确区分不同颜色的纸杯。然后，主试将每个贴纸放在纸杯上，并向被试指出，贴纸不够贴所有纸杯，有两个纸杯没有贴纸。接下来，主试告诉被试：“现在我要将贴纸藏在纸杯下面，请仔细观察。之后你需要去寻找它们。”主试把所有贴纸放到纸杯下面，并用硬壳纸盖住纸杯。主试告诉被试：“现在我旋转纸杯。然后，您可以选择一个纸杯，看看里面是否有贴纸。”主试旋转纸杯，然后取下硬壳纸板，让孩子选择。如果发现贴纸，则将纸杯拿出并放在旁边。如果没有发现贴纸，则将纸杯放回。之后，主试继续将纸杯用硬壳纸板盖起来并将托盘旋转，继续让被试重复选择。实验一直持续到被试找到所有9个贴纸或者直到旋转托盘18次为止。主试记录被试没有找到贴纸的次数(即错误次数)，理论上错误次数最大为18。将18减去错误次数作为视空工作记忆得分。视空工作记忆得分范围为0～18，得分越高，视空工作记忆越好。

5.抑制控制能力

采用Fuhs和McNeil研究[20]的“头-脚”Stroop任务和“敲-拍”Stroop任务。

“头-脚”Stroop任务：任务开始前，要求被试举起自己的利手，放于正前方。任务开始后，在主试说“头”这一口头指令时要求被试要迅速用手摸自己的脚，而在说“脚”这一指令时要用手摸自己的头。

“敲-拍”Stroop任务：任务开始前，要求被试将利手放于桌子上。任务开始后，当主试的手做出敲击桌面手势时，要求被试快速用手做出拍打桌面手势；当主试的手做出拍打桌面手势时，要求被试快速做出敲击桌面手势。

每个任务均有16个试次。实验过程中，两名主试记录被试的正确次数，被试给出的第一个反应被看作是他们的回答。例如，如果主试发出“头”的指令，被试将手移向他或她的头部，但在实际将手放在头部之前自我纠正并随后触摸了他或她的脚，那么这将被算作正确。但是，如果孩子实际上先摸了他或她的头，然后又摸了他或她的脚，这就被算作不正确。将两个任务正确次数的平均数作为抑制控制能力得分。抑制控制能力得分范围为0～16，得分越高，抑制控制能力越好。

6.数学成就

已有研究发现，数学课程测试成绩可以作为学生数学成就的有效指标[26]。因此，本研究收集所有被试最近一次数学课程测试成绩作为其数学成就得分。数学成就得分范围为0～100，得分越高，数学成就越好。

所有实验均在学生所在学校的一间空教室内进行。实验前，主试对教室进行布置，除必要的桌椅外，教室不能有任何包含文字或数字的装饰或物品，避免为被试的实验反应提供线索。每名被试单独进行一系列实验，实验时均有三名主试在场，一名主试作为实验者，负责引导被试进行实验，另两名主试作为记录者，记录被试的反应，实验全程保持安静。实验顺序与上方实验任务介绍顺序一致。每个任务开始前，实验员为被试讲解任务内容，并进行练习，直到被试正确理解任务为止。被试完成实验的时间为60～90分钟，因为时间较长，实验在连续两天内分为两次施测完成：第一次施测完成非符号数量表征比较任务、符号数量比较任务和非符号-符号数量比较任务；第二次施测完成视觉搜索任务、“头-脚”Stroop任务、“敲-拍”Stroop任务，并收集被试的人口学变量信息和最近一次数学课程测试成绩。

(三)数据处理

采用SPSS 27.0对所有被试数据进行处理，使用的统计方法包括描述性统计、Pearson相关分析和分层回归分析。

二、结果

(一)各变量描述性统计及相关分析结果

各变量描述性统计结果见表1。为分析变量间相关关系，对非符号数量表征得分、符号数量表征得分、非符号—符号数量映射能力得分、视空工作记忆得分、抑制控制能力得分和数学成就得分进行Pearson相关分析，具体结果见表1。结果发现，非符号数量表征得分与数学成就得分显著正相关，r = 0.46, p = 0.029。这说明，被试的非符号数量表征得分越高，数学成就得分越高(见图1)。此外，非符号数量表征得分与符号数量表征得分显著正相关，r = 0.44, p = 0.036。这意味着，被试的非符号数量表征得分越高，符号数量表征得分越高。其他变量间相关均不显著，ps > 0.29。

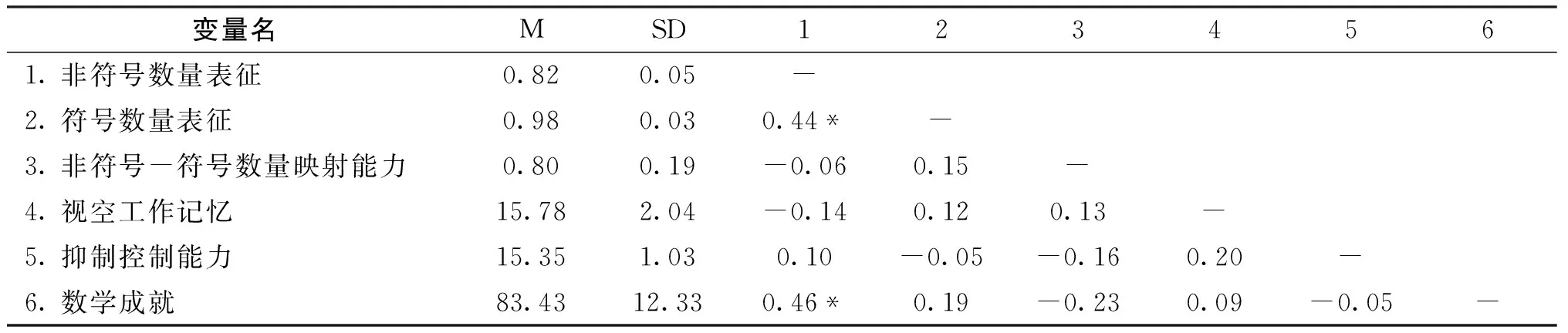
表1 各变量描述性统计分析和相关分析结果(n=23)

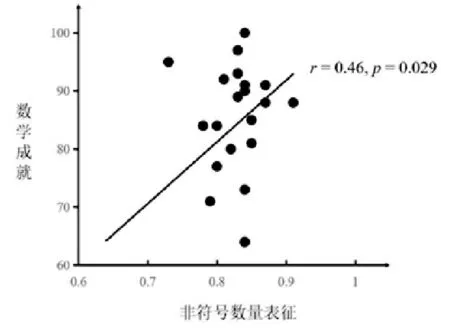
图1 非符号数量表征与数学成就相关关系散点图(注：每个实心黑点代表一个被试的原始数据，黑色直线为数据拟合线)

(二)各变量分层回归分析结果

为进一步探索非符号数量表征与数学成就的关系，以非符号数量表征得分作为预测变量，符号数量表征得分、非符号—符号数量映射能力得分、视空工作记忆得分和抑制控制能力得分为控制变量，数学成就得分作为结果变量进行分层回归分析。结果发现(见表2)，所有控制变量仅能够解释数学成就12%的变异率，p = 0.642，而非符号数量表征得分能够解释数学成就19%的变异率，非符号数量对数学成就有显著的预测作用(β=0.51，p=0.045)。这表明，非符号数量表征可能是数学成就最重要的预测因素之一。

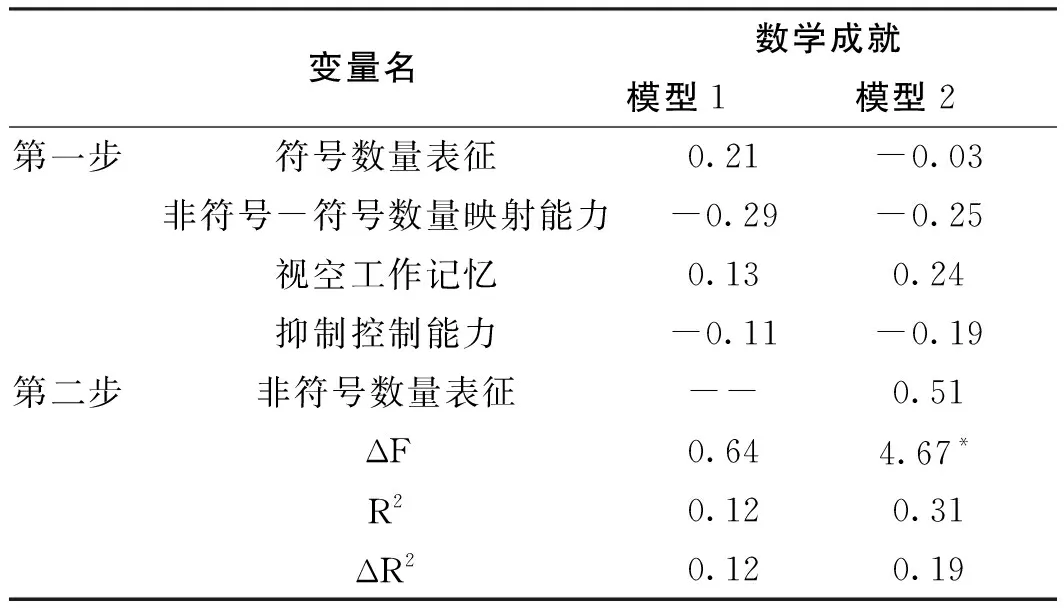
表2 各变量分层回归分析结果(n=23)

三、讨论

本研究考察了小学一年级儿童数学成就的影响因素，重点关注非符号数量表征的作用。实验结果发现，对于小学一年级儿童而言，非符号数量表征与其数学成就显著正相关，而符号数量表征、非符号-符号数量映射能力、视空工作记忆、抑制控制与数学成就之间均无显著相关。分层回归分析结果进一步发现，在控制其他变量影响条件下，非符号数量表征仍能够解释小学一年级儿童数学成就19%的变异率。研究结果支持了非符号数量表征对数学成就具有重要影响的观点，有助于为数量认知和数学教育研究领域提供相关理论依据，还有助于为刚进入数学系统学习阶段的儿童提供提升其数学成就的路径和方法。

首先，本研究发现小学一年级儿童非符号数量表征和数学成就显著正相关。这与已有研究结果一致[11][12][14][15]。也就是说，小学一年级儿童的非符号数量表征能力越好，其数学成就越高。最重要的是，分层回归分析结果进一步表明，即使控制了其他影响因素(包括符号数量表征、非符号-符号数量映射能力、视空工作记忆和抑制控制)作用的条件下，小学一年级儿童非符号数量表征仍能显著预测其19%的数学成就变异率。以上结果支持了以往研究的观点，即认为非符号数量表征是个体数学成就的重要预测因素之一[12][14]。一项汇集36项相关研究的元分析研究[10]结果发现，非符号数量表征与数学成就间存在中等强度的相关关系，并且非符号数量表征能显著预测数学成就。此外，上述结果还具有实践方面的意义。这意味着，通过提升非符号数量表征能力可能有助于提升小学一年级儿童的数学成绩。通过观察小学数学教学过程可以发现，对于小学一年级儿童来说，数学学习通常是以实物学习为主，通过直观的行动和具体的形象来理解和掌握数学知识。例如，人教版义务教育教科书《数学(一年级上册)》(2022年8月第2版)的“比多少”学习主题(第6页)，要求学生比较图画中的动物和物体的数量，如小熊的数量比木材的数量少。这一学习内容实际上就是一个非符号数量表征比较任务，涉及的就是非符号数量表征能力。这说明提升非符号数量表征已经是促进小学一年级儿童数学学习较为有效的方式之一。学校管理人员、教师和家长应该充分认识到儿童早期非符号数量表征训练的重要性，尤其是对家长而言，在生活中越早对儿童进行非符号数量表征相关的游戏活动，越能让儿童在数学系统学习中表现优异。

其次，本研究也发现符号数量表征、非符号-符号数量映射能力、视空工作记忆、抑制控制和数学成就之间均无显著相关。这一结果与已有研究不一致[19][20][22][25]。这可能有以下两个原因。第一，本研究的对象是小学一年级儿童，而以往研究的对象是幼儿园学生或小学其他年级学生[19][20][25]。年龄和年级差异可能带来符号数量表征、非符号-符号数量映射能力、视空工作记忆、抑制控制和数学成就关系的动态变化[5]。未来可以通过纵向追踪研究设计来探讨不同影响因素与数学成就间关系随着时间发展呈现出的新变化。此外，不一致结果还可能源于数学成就及其影响因素的测量方法与指标的不一致。例如，一项元分析研究[5]分析了45篇以“数量比较任务(包括非符号数量和符号数量)与数学能力关系”为主题的文章，发现数学成就及其影响因素测量方法和指标的差异可以解释14%不同文章间效应值的差异。同一实验变量(如符号数量表征)的不同测量方法和指标可能测量的该变量的不同组成部分或子变量。自然而然地，如果不同研究选取了数学成就及其影响因素的不同测量方法和指标，可能得出数学成就及其影响因素间关系的不同结果。未来研究可考虑使用多种方法和指标对数学成就和其影响因素进行测量，可以更全面地探讨数学成就与其影响因素间的关系。

虽然本研究系统探讨了小学一年级儿童非符号数量表征与数学成就的关系，但是本研究还存在一定的局限性。第一，本研究只是关注了影响小学一年级儿童数学成就的个人因素，未来研究还需要考虑人口统计学变量(如性别[27])和家庭因素(如家庭数学环境[28])的影响。第二，本研究对象是小学一年级儿童，如果想进一步了解整个小学学习过程中儿童数学成就的发展变化及其影响因素，未来研究还需增加被试群体和数量，将不同年级的学生纳入研究范围，探讨不同年级儿童之间的异同。第三，本研究将数学课程测试成绩作为数学成就指标，这样做增加了数学成就指标的生态效度，但同时也带来问题。因为数学课程测试内容非常复杂，例如根据《义务教育数学课程标准(2022年版)》的相关要求，一二年级数学课程测试内容应包括数与运算、数量关系、图形的认识与测量和数据分类等，涉及不同的数学学习领域。非符号数量表征到底是与哪种或哪几种数学成就内容相关仍是值得进一步考虑的问题。

四、结论

本研究关注小学一年级儿童数学成就的影响因素，发现非符号数量表征与数学成就显著正相关，而符号数量表征、非符号-符号数量映射能力、视空工作记忆、抑制控制与数学成就间相关不显著。在控制了符号数量表征、非符号-符号数量映射能力、视空工作记忆和抑制控制的条件下，小学一年级儿童非符号数量表征仍能显著预测其数学成就19%的变异率。这表明，非符号数量表征可能是影响小学一年级儿童数学成就最重要的因素之一，学校管理人员、教师和家长可以通过培养小学一年级儿童的非符号数量表征能力来提高儿童的数学学习质量，提升其数学成就。