低功耗嵌入式平台的SM2国密算法优化实现

刘赣秦，李晖，朱辉，黄煜坤，刘兴东

低功耗嵌入式平台的SM2国密算法优化实现

刘赣秦，李晖，朱辉，黄煜坤，刘兴东

（西安电子科技大学网络与信息安全学院，陕西 西安 710071）

随着无线通信技术的发展和智能终端的普及，越来越多的密码算法被应用到物联网设备中以保障通信安全和数据安全，其中，由国家密码管理局提出的SM2椭圆曲线公钥密码算法作为我国自主研发的椭圆曲线公钥密码算法具有安全性高、密钥短的优点，已在通信系统中广泛部署，应用于身份认证、密钥协商等关键环节。然而，由于算法涉及有限域上的大整数运算，计算开销较大，在低功耗嵌入式平台下的执行严重影响用户体验。因此，面向ARM-m系列处理器提出了一种低功耗嵌入式平台的SM2算法的高效实现方案。具体来说，通过Thumb-2指令集提供的支持处理进位和节省寻址周期，对大整数的模加、模减等基础运算进行优化，并结合平台可用寄存器的数量构建高效的基础运算模块；基于ARM-m系列处理器乘累加指令周期短的特点，优化蒙哥马利乘法实现，并结合CIOS算法设计高效的模乘方案，方案不再局限于梅森素数，极大地提高了模乘计算的速度和灵活性；在理论分析和实验测试的基础上，给出了嵌入式平台上多倍点标量乘法wNAF滑动窗法的窗长选取方法。实验测试结果表明，可有效提升资源受限的低功耗嵌入式平台中SM2算法的计算效率，不做预计算的情况下在Cortex-M3处理器上测试签名速度可达0.204秒/次，验签速度0.388秒/次，加密速度0.415秒/次，解密速度0.197秒/次。

信息安全；椭圆曲线密码体制；SM2；嵌入式平台；优化

0 引言

物联网技术出现后，因其具有使用成本低、部署难度小的特点，被广泛应用于各种领域，但在技术迅速得到发展和应用的同时，其安全问题逐渐成为关注重点。在低功耗嵌入式设备中， ARM-m系列处理器在包括微控制器、智能汽车系统、工业控制系统、智能家居以及无线网络和传感器等领域应用广泛，其中Cortex-M3处理器部署的IoT设备数量可达数十亿。为保障信息安全，需利用加密技术对信息进行保护，而通过公钥密码系统（PKC，public key cryptosystem）对数据信息进行加密或签名保护是保障网络信息安全的主要方法之一。椭圆曲线公钥密码（ECC，elliptic curve cryptography）算法的安全性基于椭圆曲线离散对数问题难以求解，在相同安全程度要求下密钥规模小于其他公钥密码系统，具有密钥短、运算快、传输效率高的特点，更适合各类资源受限的IoT设备。国家密码管理局于2010年12月17日提出了SM2椭圆曲线公钥密码算法[1]，不仅满足了各种商用密码的应用需要，也对我国信息安全体系建设有着重大意义。

然而，椭圆曲线底层运算较为复杂，执行签名、加密计算时将对资源受限的IoT设备产生大量运算压力，设计一种高效的椭圆曲线计算方案可以有效地降低服务商的设备部署成本，提升用户体验。近年来，研究人员对SM2算法针对不同应用场景需要提出了许多解决方案，大多侧重于应用方面[2-4]，对于优化实现关注较少。针对以上问题，本文基于ARM-m系列处理器特点设计并实现了一种SM2国密算法的高效计算方案。

SM2算法主要可分为4个层次，域运算层、点运算层、多倍点标量乘运算层、SM2协议层，如图1所示，其优化手段与传统ECC算法基本一致。域运算的优化实现研究主要针对计算量较大的模乘与模逆。数学家蒙哥马利（Montgomery）于1985年提出了蒙哥马利乘法[5]，极大地提高了大整数计算模乘的速度，Koc等[6]在此基础上对蒙哥马利约减算法的步骤进行整合，提出了5种优化的蒙哥马利约减算法，进一步提高了效率；文献[7]提出了梅森素数法，对于特定素数效率有所提高。而近年来对于模乘的优化研究偏重于硬件层面，Aashish等[8]设计了Montgomery 乘法器，有效地提高了模乘吞吐量，文献[9]设计了基于硬件的交叉模乘；面向嵌入式平台，王腾飞等[10]提出一种基于协处理器指令的优化方案，同样加快了计算速度；但基于硬件的方法存在灵活性缺陷，将现有的各类嵌入式设备进行硬件升级成本较大。两乘数相等计算大整数平方时，在一些算力较强的平台上表现较好的一种思路是利用Karatsuba算法和ToomCook算法[11]对平方计算进行加速；针对支持64位运算的平台，李斌等[12]提出了结合硬件KOA乘法和梅森素数法的模乘方案。对于大整数模逆的优化计算，Hossain等[13]提出了基于扩展Euclid算法的模逆算法，面向GPU等平台Zhou等[14]设计了利用费马小定理计算模逆的方案，文献[15]在此基础上进一步缩短了所需加法链。对于ECC的上层运算，文献[16]针对ECC的点运算进行优化，分析了各类坐标系下计算的优劣，取得了约 30%的计算速度提升。混合坐标法[17]由Cohen提出，讨论了求逆与模乘时间比不同时各类混合坐标系的优劣性。文献[18]提出了ECC标量乘法对使用预处理及窗口技术提高点乘计算效率的思想。由Longa提出的m-DBL算法[19]基于模乘与模平方效率不同，将重复倍点运算中的模乘转化为模平方来加速运算；文献[20]介绍了用预计算的查表法对固定点标量乘法进行加速；文献[21]利用可并行的蒙哥马利点乘加速了多倍点标量乘法运算。但此类方法大多针对强算力平台，对于各种资源受限的嵌入式平台，由于对平台的一些特点缺乏针对性，如存储受限、并行效率差，实测时计算缓慢，效果欠佳。

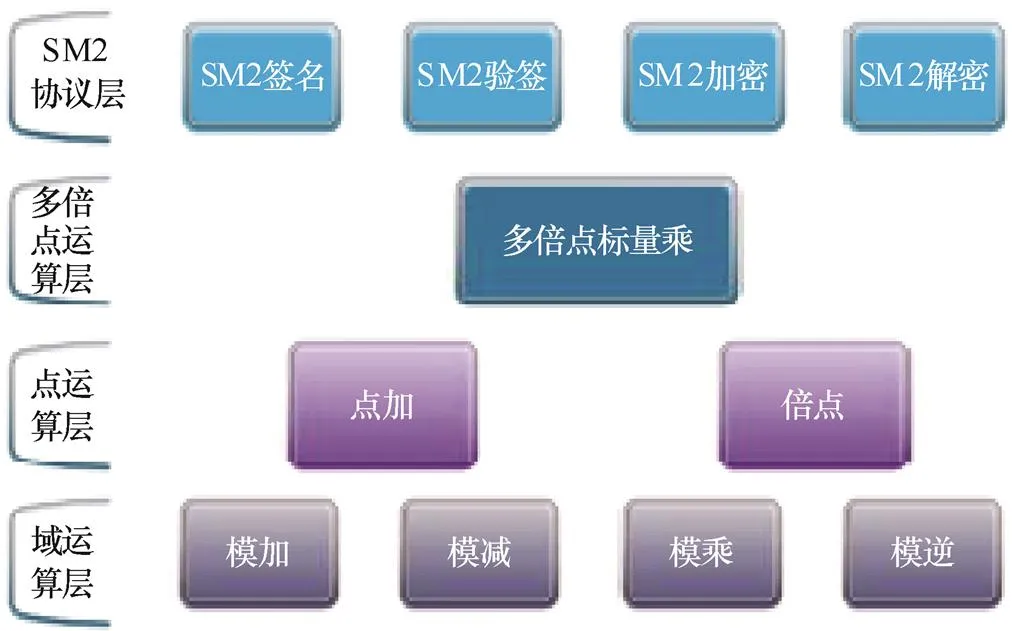
图1 SM2算法层次

Figure 1 Structure of algorithm SM2

本文针对SM2国密算法，充分利用低功耗嵌入式平台特点，对椭圆曲线密码体制的底层运算进行优化实现研究，对算法的一些关键步骤进行改进，主要贡献包括以下几个方面。

1) 结合ARM-m系列MCU访存开销大的特点，构建了基于Thumb-2指令集的大整数模加、模减基础运算模块，结合平台可用寄存器的数量进行高效分配，相比LibTomMath开源库实现的模加方案性能提升2.42倍。

2) 考虑平台并行效率不高以及访存较慢的特点，优化了蒙哥马利乘法，并结合CIOS算法设计了高效的模乘方案，效率超过了在大部分平台上表现较好的梅森素数法和其他各种公开算法，同时避免了梅森素数法对于特定素数的限制问题，提高了算法灵活性，签名效率相比梅森素数法提升约6.13%。

3) 为存储受限环境高效计算ECC多倍点标量乘法提供了解决方案，利用NAF算法计算多倍点标量乘法，分析了使得预计算和乘法阶段时间总和最短的窗长选取，并通过实验测试验证了结论。

4) 在搭载Cortex-M3处理器的开发板上应用优化方案实现了使用256位素域椭圆曲线的SM2签名、验签、公钥生成以及加解密算法，并进行了各项对比测试。实验测试证明提出的优化方案效果显著，达到了0.205次/秒签名，0.415次/秒加密速度，相比LibTomMath开源库实现的版本签名性能提升1.62倍，加密性能提升1.59倍。

1 背景知识

1.1 SM2数字签名算法

1.2 SM2加密算法

1.3 椭圆曲线定义及坐标表示

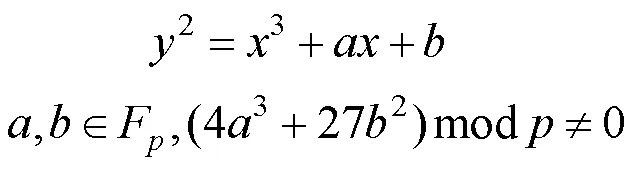
1.4 蒙哥马利乘法

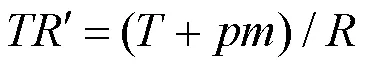
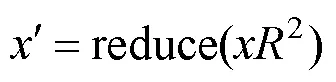
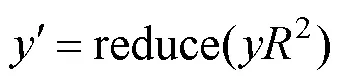
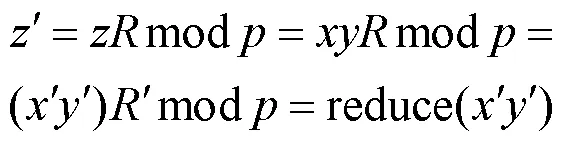
1.5 扩展欧几里得算法

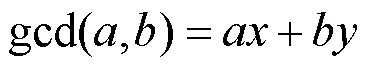
1.6 Cortex-M3及Thumb-2指令集

ARM公司为了更好适应微控制器和受限的节能应用需求，设计了ARM-m系列处理器，其中Cortex-M3处理器应用广泛，采用ARMv7-M架构，包括所有的16位Thumb指令集和基本的32位Thumb-2指令集架构。Thumb-2在Thumb指令集架构（ISA，instruction set architecture）上进行了大量的改进，它与Thumb相比，具有更高的代码密度并提供16/32位指令的更高性能。部分Thumb-2指令集如表1所示。

2 域运算优化

SM2算法中基础四则运算涉及的操作数均为256位大整数，运算在有限域中进行。根据Gura等[24]的研究，MCU平台开销最大的操作为访存，因此算法优化时应尽可能减少访存次数，将常用字段放在寄存器中。本节介绍面向低功耗嵌入式平台的域运算构建和优化方法，对资源有限的寄存器进行合理利用。

表1 部分Thumb-2指令集

2.1 快速模加减

模加减所得结果为有限域中的元素，在采用标准进制表示时，被存储在一组机器字中，以Cortex-M3平台的32位架构为例，机器字可表示为16、32位整型或64位浮点型。由文献[25]可知，浮点型对字的利用率低，仅有31.25%。而16位及32位带符号整型对字的利用率均不及32位无符号整型。因此，本文存储256位整数时均使用32位无符号整型。有限域中256位模加计算过程如算法1所示。

算法1 256位模加

输入 加数，加数，素域

3) 对从7到0，重复执行

5) 对从1到7，重复执行：

图2 指令集处理256位模加示意

Figure 2 The instruction set handles 256 bit modules plus

图3 指令集处理256位减法示意

Figure 3 The instruction set handles 256-bit subtraction

表2 通用寄存器的分配

2.2 改进的蒙哥马利模乘

模乘的执行过程通常可分为两个阶段，蒙哥马利乘法[5]和梅森素数法[7]。首先计算256位乘法，再计算模约减。考虑MCU平台通常搭载嵌入式实时操作系统，并行效率低；并且，测试中模平方的按位二次展开法效果不佳，因此舍弃了蒙哥马利乘法中的相关步骤。由1.4节介绍的蒙哥马利乘法，注意到

使用式(11)计算时，相比1.4节中介绍的蒙哥马利乘法，仅计算两次蒙哥马利约减和两次256位乘法。进一步，可将乘法和约减步骤结合考虑，本文基于CIOS（coarsely integrated operand scanning）算法[6]对蒙哥马利约减算法进行优化，调整蒙哥马利乘法的循环体和乘法计算顺序，整合了乘法和约减过程。整个计算过程分为一层外循环和两层内循环，基于大整数运算的分段思想，外循环拆解乘数至32位，第一层每次取的32位在结果数组中乘累加，第二层计算取约减数再次乘累加，由于结果数组的部分可常驻寄存器，相比先相乘后约减的模乘计算方式有效降低了访存次数。蒙哥马利约减算法如算法2所示。

算法2 蒙哥马利约减算法

对从0到7，重复执行

算法3 改进的蒙哥马利模乘算法

3 多倍点标量乘法优化

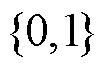
算法4NAF标量表示算法

输入 标量

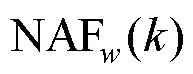
算法5NAF标量乘法算法

显然，算法效率与标量的汉明重量（非0元素个数）有关，标量表示算法可以有效降低标量的汉明重量。其他标量乘法算法亦可分为预计算和乘法执行两阶段，即通过预计算临时存储得到的结果对乘法执行过程进行加速。一般地，预计算得到结果越多，乘法执行时越快，预计算时间也会增长，所以考虑两阶段开销总和作为算法整体性能标准。计算固定点的乘法时，预计算所得结果可在多次乘法中重复使用，此时预计算所耗时间可忽略不计。考虑低功耗嵌入式设备中存储资源有限，存储一张预计算的乘法表会占用较多存储资源，因此假设预计算结果仅用于一次乘法。忽略对点求加法逆的开销，标量长度为256时，考虑最坏情形下（即标量二进制表示汉明重量为256）的NAF标量乘法计算量如表3所示。

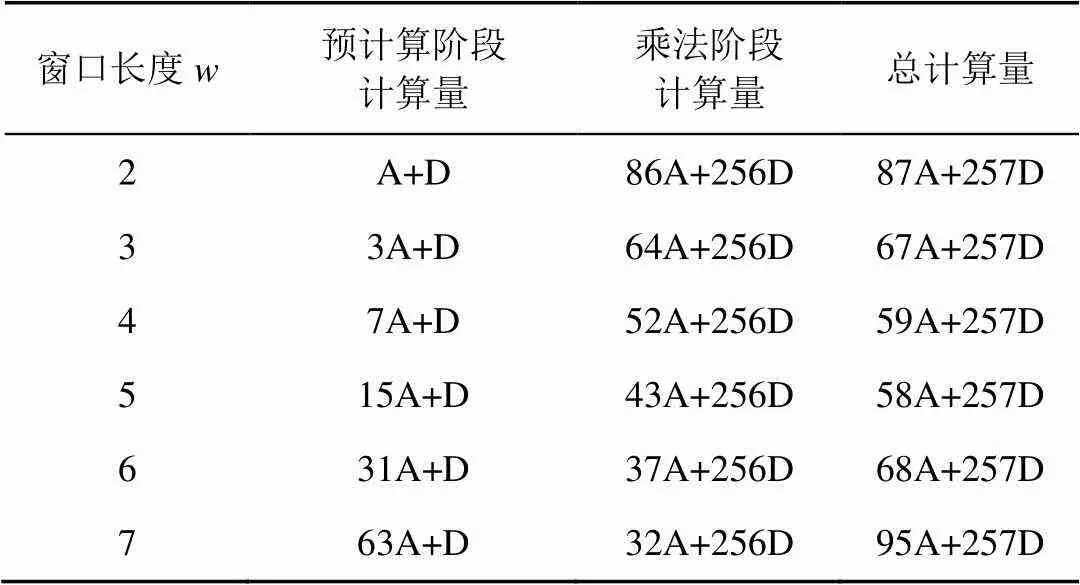
表3 256位标量计算量

注：A代表点加运算，D代表倍点运算

预计算阶段开销随增大呈指数型增长，同时乘法阶段计算量的减少量逐渐下降。算法实质上是通过NAF重编码算法获得的标量中的汉明重量减少，从而减少点加计算次数，提高了多倍点标量乘法的整体性能。

4 实验分析

本节给出优化实现的SM2国密算法的性能数据，使用了基于Tom StDenis编写的LibTomMath开源大数运算库实现的SM2国密算法作为对比。测试时使用椭圆曲线及有限域参数均为文献[28]中给定参数。

本文进行测试的硬件环境为搭载cortex-M3的STM32F103ZET6开发板和ST-Link下载器，系统时钟频率为72 MHz（STM32F103ZET6有5个时钟源，最大频率为72 MHz），存储flash为512 kB；软件环境为keil5.0编译器。编译参数使用了-O3、-Otime、--apcs=interwork，用于开启编译器优化和thumb指令集和ARM指令集混合调用。以运行时间作为评价指标，将设计的方案与一些其他公开算法进行对比评测。

对于基础运算模块，为避免次数较少、特殊数据的影响，通过重复执行10次公钥生成过程在keil5.0中的Simulator对本文实现的模加模块和LibTomMath开源大数运算库中的模加模块进行对比测试，由于库中大数结构体定义较为复杂，对其进行了精简，限定为256位整数，结果如表4所示，共执行44 200次，可见本文设计的基于Thumb-2指令集的优化方案使模加算法的执行效率提升明显，性能提升2.42倍。

表4 素数域模加测试结果

同样地，在开发板上实现设计的模乘方案和一些其他公开算法，进行对比评测。由于模乘在整个SM2算法中开销占比约70%，以随机生成的相同公私钥对整个SM2协议运行时间进行测试，通过JTAG调试模块记录时间，结果如表5所示。

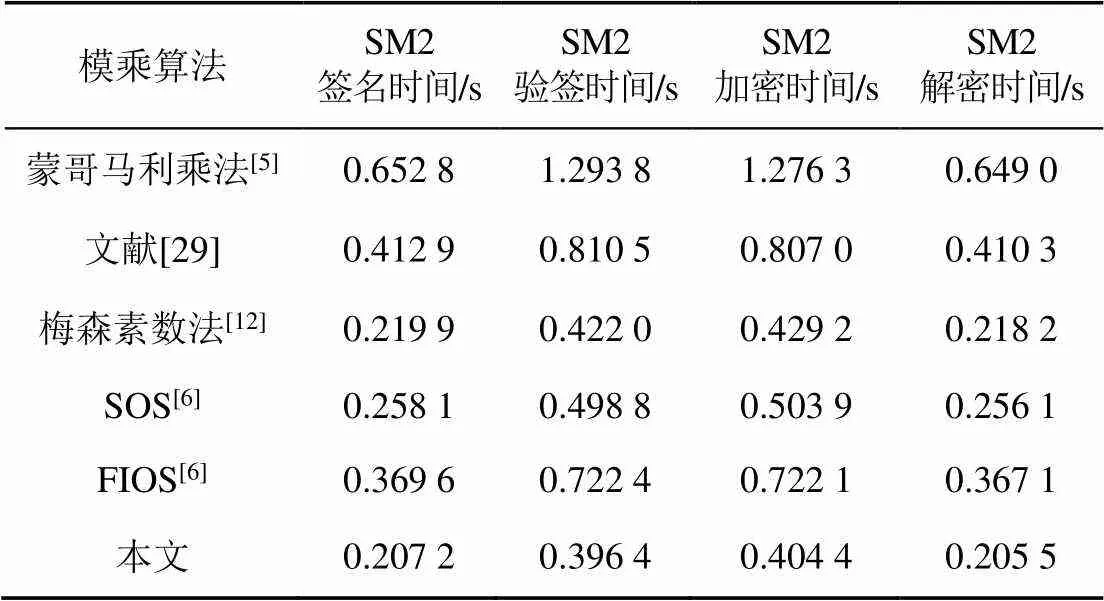
表5 不同模乘算法下SM2算法性能测试结果

由于平台本身不支持模平方的加速算法，同时结合MCU平台访存开销大的特点，设计的模乘方案优于强算力平台中表现较好的梅森素数法，且避免了对素数的限定，更广泛适用于实际环境中各种需要更换椭圆曲线参数来提高安全性的需求，同时兼顾SM2国密算法中的模运算和模运算，亦可在其他需计算大整数模乘的密码算法中推广。

为了测评多倍点标量乘法中的标量表示算法，对1 000次未知点多倍点标量乘法计算时间进行测试对比，结果如图4所示，其中预计算开销如表6所示。

图4 多倍点标量乘法测试结果

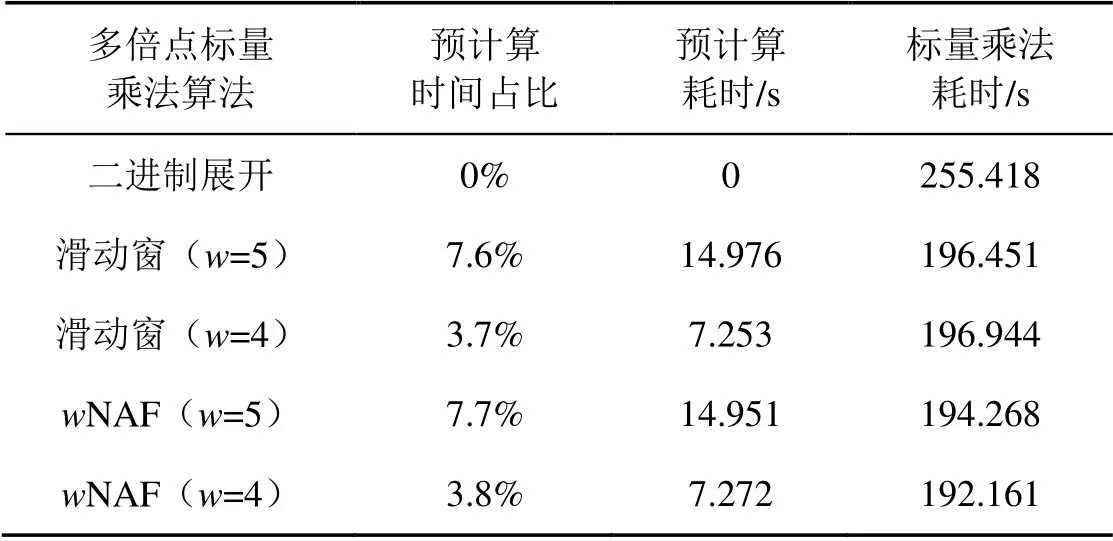
表6 预计算开销分析

结果表明，取=4时的NAF算法效果最佳。由表3可知，最坏情形时取5较取4少计算一次点加，但实际情况中标量的汉明重量通常少于最坏情形，故考虑预计算结果仅用于一次乘法时，应取=4，适用于未知点乘法，对于固定点乘法预计算时间可忽略不计，此时窗长取值可视存储情况而定。

与基于LibTomMath库构建基础运算的实现的SM2算法进行对比测试，同时对本文设计的SM2国密算法优化方案的整体性能表现进行评估。对签名、验签、公钥生成、加密、解密运算各执行1 000次取平均值，结果如图5所示，单次签名速度可达0.205秒/次，加密速度0.415秒/次，显著优于基于开源库LibTomMath实现的SM2国密算法，签名性能提升1.62倍，加密性能提升1.59倍。

图5 SM2算法测试结果

5 结束语

本文面向低功耗嵌入式平台设计了SM2算法的优化实现方案，其中通过Thumb-2指令集的支持构建了高效的模加减运算模块，对上层运算提供支持；结合低功耗嵌入式平台访存慢、并行效率低的特点，基于蒙哥马利乘法进行改良，并结合CIOS算法设计了高效的模乘计算方案，相比梅森素数法提高了灵活性和效率。实验结果表明，本文给出的优化实现能有效地提升SM2算法的计算速度，实验测试中达到了0.205秒/次签名，0.415秒/次加密速度，可以更好地满足在低功耗嵌入式设备上高效计算签名与加密的需求，具有非常高的实际应用价值。

[1] 国家密码管理局. SM2椭圆曲线公钥密码算法第1部分: 总则: GM/T 0003.1-2012[S]. 北京:中国标准出版社, 2012:8.

State Cryptography Administration. SM2 elliptic curve public key cryptography algorithm part 1: general provisions: GM/T 0003.1-2012[S].8 Beijing: China Standard Press, 2012: 8.

[2] 罗玙榕, 曹进, 李晖, 等. 基于SM2联合签名的电子发票公开验证方案[J]. 网络与信息安全学报, 2022, 8(2): 122-131.

LUO Y R, CAO J, LI H, et al. Electronic invoice public verification scheme based on SM2 joint signature [J]. Journal of Network and Information Security, 2022, 8(2): 122-131.

[3] 陈锋, 邹洪, 吴亚楠, 等. 基于SM2密码体系的电力信息安全监控系统设计[J]. 电子设计工程, 2022, 30(5):100-103, 108.

CHEN F, ZOU H, WU Y N, et al. Design of power information security monitoring system based on sm2 cipher system[J]. Electronic Design Engineering, 2022, 30(5):100-103, 108.

[4] 程朝辉. 基于SM2的无证书加密算法[J]. 密码学报, 2021, 8(1): 87-95.

CHENG C H. Certificateless encryption algorithm based on SM2 [J]. Journal of Cryptography, 2021, 8(1): 87-95.

[5] MONTGOMERY P L. Modular multiplication without trial division[J]. Mathematics of Computation, 1985, 44(170): 519-521.

[6] KOC C, ACAR T, JR B. Analyzing and comparing montgomery multiplication algorithms[J]. Micro, IEEE, 1996, 16(3): 26-33.

[7] SOLINAS J A. Generalized mersenne numbers[M]. Faculty of Mathematics, University of Waterloo, 1999.

[8] PARIHAR A, NAKHATE S. High-speed high-throughput VLSI Architecture for RSA montgomery modular multiplication with efficient format conversion[J]. Journal of the Institution of Engineers (India) Series B, 2019, 100(2): 217-222.

[9] RAHMAN M S, HOSSAIN M S, RAHAT E H, et al. Efficient hardware implementation of 256-bit ECC processor over prime field[C]//2019 International Conference on Electrical, Computer and Communication Engineering (ECCE). 2019: 1-6.

[10] 王腾飞, 张海峰, 许森. SM2专用指令协处理器设计与实现[J].计算机工程与应用, 2022, 58(2): 102-109.

WANG T F, ZHANG H F, XU S. Design and implementation of SM2 special instruction coprocessor[J]. Computer Engineering and Applications, 2022, 58(2): 102-109.

[11] DING J N，LI S G，GU Z. High-speed ECC processor over NIST prime fields applied with toom–cook multiplication[J]. IEEE Transactions on Circuits and Systems I, 2019, 66(3): 1003-1016.

[12] 李斌, 周清雷, 陈晓杰, 等. 可重构的素域SM2算法优化方法[J].通信学报, 2022, 43(3): 30-41.

LI B, ZHOU Q L, CHEN X J, et al. Optimization of reconfigurable SM2 algorithm over prime field[J]. Journal of Communication, 2022, 43(3): 30-41.

[13] HOSSAIN M S, KONG Y. High-performance FPGA implementation of modular inversion over F_256 for elliptic curve cryptography[C]//2015 IEEE International Conference on Data Science and Data Intensive Systems. 2015: 169-174.

[14] ZHOU L, SU C, HU Z, et al. Lightweight implementations of NIST P-256 and SM2 ECC on 8-bit resource-constraint embedded device[J]. ACM Transactions on Embedded Computing Systems (TECS), 2019, 18(3): 1-13.

[15] 朱辉, 黄煜坤, 王枫为, 等. 一种基于图形处理器的高吞吐量 SM2 数字签名计算方案[J]. 电子与信息学报, 2022, 44(10): 1-10.

ZHU H, HUANG Y K, WANG F W, et al. A high throughput SM2 digital signature computing scheme based on graphics processor[J]. Journal of Electronics and Information Technology, 2022, 44(10): 1-10.

[16] LONGA P, GEBOTYS C. Efficient techniques for high-speed elliptic curve cryptography[C]//International Workshop on Cryptographic Hardware and Embedded Systems. Heidelberg, 2010: 80-94.

[17] COHEN H, MIYAJI A, ONO T. Efficient elliptic curve exponentiation using mixed coordinates[C]//International Conference on the Theory and Application of Cryptology and Information Security. 1998: 51-65.

[18] SETIADI I, KISTIJANTORO A I, MIYAJI A. Elliptic curve cryptography: Algorithms and implementation analysis over coordinate systems[C]//2015 2nd International Conference on Advanced Informatics: Concepts, Theory and Applications (ICAICTA). 2015: 1-6.

[19] LONGA P, MIRI A. Fast and flexible elliptic curve point arithmetic over prime fields[J]. IEEE Transactions on Computers, 2008, 57(3): 289-302.

[20] HANKERSON D, MENEZES A J, VANSTONE S. Guide to elliptic curve cryptography[M]. Springer Science & Business Media, 2006.

[21] ISLAM M M, HOSSAIN M S, HASAN M K, et al. FPGA implementation of high-speed area-efficient processor for elliptic curve point multiplication over prime field[J]. IEEE Access, 2019, 7: 178811-178826.

[22] 国家密码管理局. SM3 密码杂凑算法: GMT 0004.4-2012[S]. 北京:中国标准出版社, 2012:8.

National Cryptography Administration. SM3 password hashing algorithm: GMT 0004.4-2012[S]. Beijing: Standards Press of China, 2012:8.

[23] RIVAIN M. Fast and regular algorithms for scalar multiplication over elliptic curves[J]. Cryptology ePrint Archive, 2011.

[24] GURA N, Patel A, Wander A, et al. Comparing elliptic curve cryptography and RSA on 8-bit CPUs[C]//International Workshop on Cryptographic Hardware and Embedded Systems. 2004: 119-132.

[25] Advanced Micro Devices, Inc. AMD graphic core next[R]. Advanced Micro Devices, Inc, 2011.

[26] DUSSE S R, KALISKI B S. A cryptographic library for the Motorola DSP56000[C]//Workshop on the Theory and Application of Cryptographic Techniques. 1990: 230-244.

[27] MUIR J, STINSON D. Minimality and other properties of the width-𝑤 nonadjacent form[J]. Mathematics of Computation, 2006, 75(253): 369-384.

[28] 国家密码管理局. SM2椭圆曲线公钥密码算法第5部分:参数定义: GMT 0003.4-2012[S]. 北京: 中国标准出版社, 2012.

National Cryptography Administration. SM2 Elliptic curve public key cryptography algorithm Part 5: Parameter definition: GMT 0003.4-2012[S]. Beijing: Standards Press of China, 2012.

[29] 闫闵. 基于GPU的SM2数字签名和验证算法的快速实现与优化[D]. 上海: 上海交通大学, 2020.

YAN M. Fast implementation and optimization of SM2 digital signature and verification algorithm based on GPU [D]. Shanghai: Shanghai Jiaotong University, 2020.

Public key cryptographic algorithm SM2 optimized implementation on low power embedded platform

LIU Ganqin, LI Hui, ZHU Hui, HUANG Yukun, LIU Xingdong

School of Cyber Engineering, Xidian University, Xi’an 710071, China

With the development of wireless communication technology and the popularization of intelligent terminals, more and more cryptographic algorithms are applied to IoT devices to ensure the security of communication and data. Among them, the SM2 elliptic curve public key cryptography proposed by the State Cryptography Administration is an elliptic curve public key cryptography algorithm developed domestically, which has the advantages of high security and short key. SM2 has been widely deployed in various communication systems and is used in essential parts such as identity authentication and key negotiation. However, since SM2 involves large integer operations on finite fields, the computational cost is high, and its execution on a low-power embedded platform seriously affects the user experience. Therefore, an efficient implementation scheme of SM2 algorithm for low-power embedded platform was proposed for ARM-m series processors. Specifically, Thumb-2 instruction set was adopted to handle carry and save addressing cycles, basic operations such as modulo addition and sub-traction of large integers were optimized, and the number of available registers on the platform was combined to build efficient basic operations. Besides, based on the short multiplication and accumulation instruction cycle of ARM-m series processors, the implementation of Montgomery multiplication was optimized, and an efficient modular multiplication scheme was designed in combination with the CIOS algorithm. The scheme was no longer limited to Mersenne primes, and greatly improved the speed and flexibility of modular multiplication. Based on the theoretical analysis and experimental test, the window length selection method of the multiple point-scalar multiplication wNAF sliding window method on the embedded platform was given. The experimental test results show that the proposed scheme can effectively improve the computational efficiency of the SM2 algorithm on the resource-constrained low-power embedded platform. Without pre-calculation, the test signature speed can reach 0.204s/time, the signature verification speed is 0.388s/time, the encryption speed is 0.415s/time, and the decryption speed is 0.197s/time.

information security, elliptic curve cryptosystem, SM2, embedded platform, optimization

TP393

A

10.11959/j.issn.2096−109x.2022080

2022−05−16；

2022−07−05

朱辉，zhuhui@xidian.edu.cn

国家自然科学基金（61972304, 61932015），陕西省重点产业创新链项目（2020ZDLGY08-04）

The National Natural Science Foundation of China (61972304, 61932015), Natural Science Foundation of Shaanxi Province (2020ZDLGY08-04)

刘赣秦, 李晖, 朱辉, 等. 低功耗嵌入式平台的SM2国密算法优化实现[J]. 网络与信息安全学报, 2022, 8(6): 29-38.

LIU G Q, LI H, ZHU H, et al. Public key cryptographic algorithm SM2 optimized implementation on low power embedded platform [J]. Chinese Journal of Network and Information Security, 2022, 8(6): 29-38.

刘赣秦（1998−），男，江西莲花人，西安电子科技大学硕士生，主要研究方向为密码算法的高性能优化。

李晖（1968−），男，河南灵宝人，博士，西安电子科技大学教授、博士生导师，主要研究方向为密码学、无线网络安全、云计算安全、信息论与编码理论。

朱辉（1981−），男，河南周口人，博士，西安电子科技大学教授、博士生导师，主要研究方向为数据安全与隐私保护、安全方案及协议设计、网络及应用安全。

黄煜坤（1998−），男，湖北襄阳人，西安电子科技大学硕士生，主要研究方向为密码算法的高性能优化。

刘兴东（1992−），男，湖南衡阳人，西安电子科技大学硕士生，主要研究方向为网络空间安全、可信执行环境、密码算法优化。