发动机主轴滚子轴承铣削加工稳定性模糊控制方法的研究

孟 扬

(淮南职业技术学院， 安徽 淮南 232001)

0 前 言

滚子轴承是发动机主轴的关键部件之一[1]，其可靠性、精度是决定发动机性能的关键因素。滚子轴承运行工况具有转速高、载荷轻、工作环境温度高、内外圈同向转动等特点。滚子轴承容易出现打滑、歪斜、摩擦等情况，从而使其出现一定程度的磨损，最终导致加工失效。

滚子轴承主要采用铣削加工的方式。在实际生产过程中，机床常常发生颤振，从而使滚子轴承的加工质量下降，最终影响滚子轴承的使用效果与寿命[2]。铣削加工颤振主要由机床部件、切削加工与外部振源产生，颤振不但会影响加工的表面形状与精度，还会使工件的生产率降低，并伴随着较大噪声，极易损害铣削加工人员的健康。由此可见，精准控制铣削加工的稳定性是提高滚子轴承加工质量的关键，也是滚子轴承铣削加工领域亟待解决的问题之一。为了满足上述需求，本次研究提出了轴承铣削加工稳定性模糊控制方法。

1 滚子轴承铣削加工稳定性研究

1.1 滚子轴承铣削加工模型构建

要提高铣削加工稳定性模糊控制的效果，首要任务是构建滚子轴承铣削加工模型，为后续稳定性控制的实现奠定坚实的基础[3]。

滚子轴承铣削加工主要包括正交切削、斜角切削与圆柱螺旋立铣刀切削等3种方式，滚子轴承铣削加工模型示意图如图1所示。

图1 滚子轴承铣削加工模型示意图

以滚子轴承铣削加工模型为基础，计算不同铣削加工方式的单位切削能，其表达式如式(1)-式(3)所示：

(1)

(2)

(3)

式中：Uo1、Uo2与Uo3分别表示正交切削、斜角切削、圆柱螺旋立铣刀切削方式的单位切削能；Uo表示标定单位切削能；θ与θo分别表示刀具等效前角及其标定值；a0表示标定切削厚度；fa表示每齿进给量；χ表示顺铣与逆铣的划分阈值[4]。

1.2 滚子轴承铣削加工颤振机理分析

以滚子轴承铣削加工模型为基础，深入分析铣削加工的颤振机理，为后续稳定性预测提供基础。在实际应用过程中，铣削加工颤振大部分属于自激振动的再生型颤振。滚子轴承铣削加工立面如图2所示。

图2 滚子轴承铣削加工立面示意图

铣刀是多齿结构，在滚子轴承加工过程中，铣刀对工件表面进行不连续切削，j刀齿工作在j-1刀齿加工过的工件表面，每个刀齿在作业过程中均会产生振纹，但相邻刀齿产生的振纹具有相位差异，两者无法完全重合，这会使切削厚度发生一定变化，进而对单位切削能产生影响[5]。随着滚子轴承铣削加工的进行，切削厚度实时发生变化。若切削厚度一直加大，就会使铣削加工的不稳定性增强，从而影响铣削加工的正常进行。当切削厚度变化维持在一定范围时，颤振不会对加工稳定性产生较大的影响，可以维持铣削加工的正常进行[6]。

1.3 滚子轴承铣削加工稳定性预测

以铣削加工颤振机理为依据，构建相应的滚子轴承铣削加工稳定性预测模型，并对其进行求解，以获得准确的铣削加工颤振频率。

滚子轴承铣削加工过程中，切削厚度处于实时变化的状态，其表达式如式(4)所示：

b(t)=(ΔR(t)sinψ-Δz(t)cosψ)g(φ)

(4)

式中：b(t)表示t时刻对应的切削厚度；ΔR(t)表示刀具整体动态位移；ψ表示切削位置的偏转角；Δz(t)表示z方向的动态位移；g(φ)表示单位跃阶函数，可反映刀齿切削的实时状态[7]。

单位跃阶函数g(φ)是求解切削厚度的关键参量，其取值规则如式(5)所示：

(5)

式中：φ0表示刀齿的切入角；φ1表示刀齿的切出角。

铣削力也是影响加工稳定性的关键因素之一[8]，其计算公式如式(6)所示：

(6)

式中：fx(t)、fy(t)、fz(t)分别表示x、y、z方向的动态铣削力；γ(t)表示方向因子；δ1、δ2、δ3分别表示切向、径向与轴向的切削力系数；c表示轴向铣削深度。

采用傅里叶级数[9]平均数表示初始方向因子，其表达式如式(7)所示：

(7)

式中：γ(0)表示初始方向因子；N表示刀具刃的数量；T表示铣削周期。

根据确定的初始方向因子，计算再生切削厚度产生的铣削力，其计算公式如式(8)所示：

(8)

式中：f表示再生切削厚度产生的铣削力；c′表示再生切削的厚度；Δη表示再生位移。

根据再生位移变化特征，构建铣削加工稳定性预测模型，其表达式如式(9)所示：

Δη=(1-μ-ωtT)G(ωt)f

(9)

式中：μ-ωtT表示预测模型辅助参量；ωt表示时刻t对应的颤振频率；G(ωt)表示颤振频率响应函数[10]。

通过求解式(9)可获得铣削加工颤振频率ωt，将其与设定阈值进行比较，即可确定铣削加工的稳定性，判定规则如式(10)所示：

(10)

式中：Γ表示设定阈值，需要根据实际工件情况设置。

通过铣削加工稳定性预测模型可获得铣削加工过程的颤振频率[11]，从而判定铣削加工稳定状态。

1.4 铣削加工稳定性模糊控制

以铣削加工稳定状态为依据，设计模糊PID控制器，制定颤振频率模糊PID控制流程，实现铣削加工稳定性的模糊控制[12]。

常规PID控制器不能同时整定参数ξP、ξI与ξD，无法满足铣削加工稳定性的控制需求，故引入模糊集合理论对参数进行自适应整定，使PID控制器具备更好的控制性能，这种控制器被称为模糊PID控制器。

模糊PID控制器可根据不同时刻的偏差与偏差变化率对参数ξP、ξI与ξD进行实时整定，实时输出控制参量，将颤振频率控制在安全范围内[13]。模糊PID控制器实质就是寻找参数、偏差与偏差变化率之间的模糊关系，建立相应的函数关系，其表达式如式(11)所示：

(11)

式中：η(·)表示模糊控制函数；λ与λe分别表示偏差与偏差变化率。

将λ与λe模糊化为τ与τe，结合铣削加工稳定性的控制需求，将其转化为计算机语言，τ,τe={A,B,C,O,D,E,F}，分别代表负大、负中、负小、零、正小，正中与正大[14]。将λ与λe的变化范围定义为一定的模糊论域，将其划分为7档，λ,λe={-5,-3,-1,0,1,3,5}。在滚子轴承铣削加工过程中，计算某时刻颤振频率与阈值之间的差值，将其作为偏差λ(t)，偏差变化率为λe(t)=λ(t)-λ(t-1)[15]。将λ(t)与λe(t)输入模糊PID控制器，输出数值即为控制参数整定数值ΔξP、ΔξI与ΔξD，从而确定最终的控制参数，其表达式如式(12)所示：

(12)

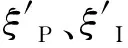
根据控制参数对铣削加工过程进行实时控制，可以保障铣削加工的稳定性，提升滚子轴承的加工质量。

2 实验结果分析

2.1 铣削加工框架的搭建与实验参数的标定

选取某型号铣削设备作为实验装置，将整个铣削加工过程设置为一个恒力闭环结构，铣削加工框架如图3所示。

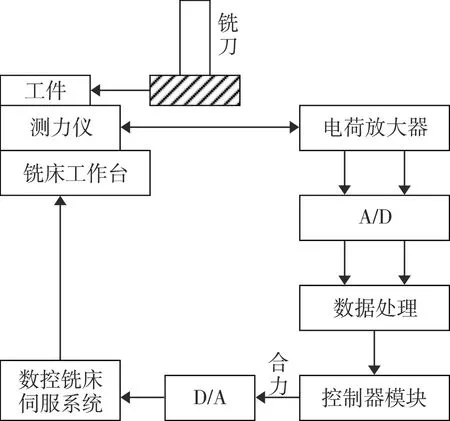
图3 铣削加工框架示意图

为了方便实验，标定滚子轴承工件的进给速度，其与伺服控制电压之间的关系如式(13)所示：

v=439.28u+15.38

(13)

式中：v表示标定的滚子轴承工件进给速度；u表示伺服控制电压。

2.2 模糊规则的确定

应用模糊集合理论，根据τ与τe设置相应的模糊规则，控制参量模糊规则如表1所示。

将如表1所示的控制参量模糊规则映射到{-5,-3,-1,0,1,3,5}论域中，即可获得控制参数查询表。

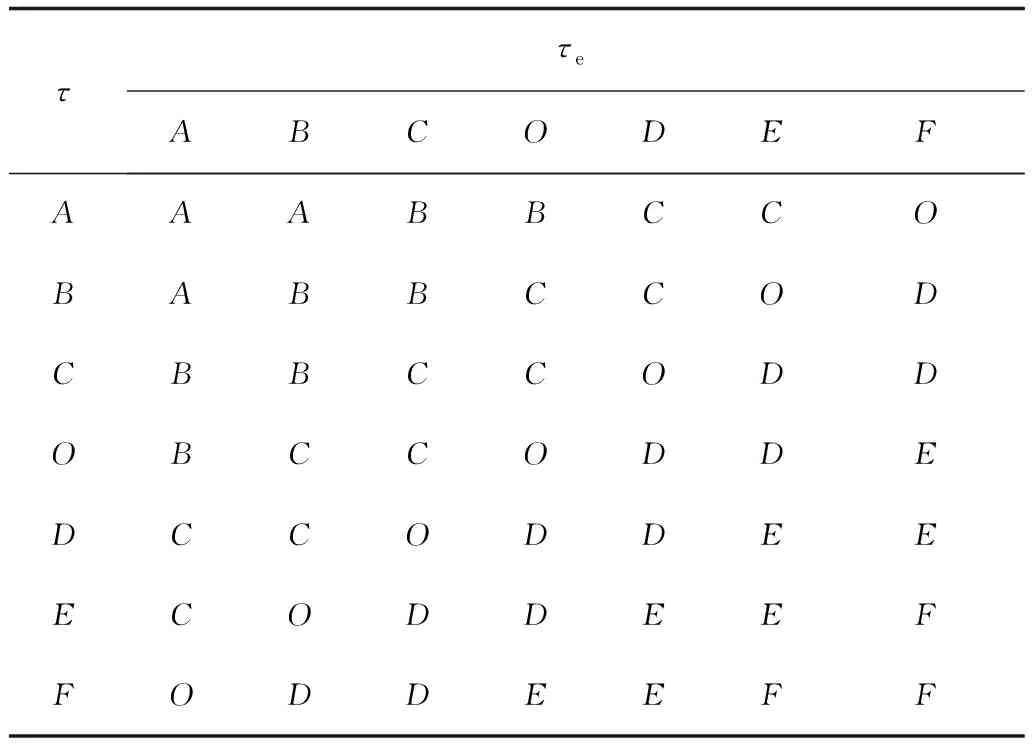
表1 控制参量模糊规则

2.3 结果分析

根据相关要求进行滚子轴承铣削加工稳定性模糊控制实验，通过铣削加工颤振频率与滚子轴承表面振纹情况来验证本次所提方法的稳定性控制效果。

2.3.1 铣削加工颤振频率分析

通过实验获得铣削加工颤振频率，如图4所示。模糊控制前铣削加工颤振频率大部分在稳定性判定阈值之上，铣削加工稳定性较差，符合稳定性控制实验需求。模糊控制后，铣削加工颤振频率得到了有效的控制，保持在稳定性判定阈值之下，最终稳定在10 Hz左右。

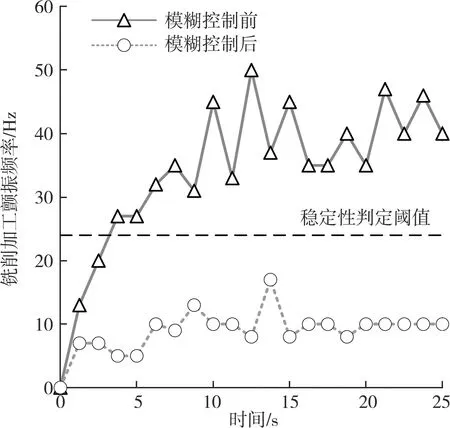
图4 铣削加工颤振频率图

2.3.2 滚子轴承表面振纹分析

滚子轴承表面振纹如图5所示。模糊控制前，滚子轴承表面存在大量振纹，影响了滚子轴承的加工质量与性能发挥。模糊控制后，滚子轴承表面振纹明显减少，甚至消失。

图5 滚子轴承表面振纹示意图

实验结果表明，模糊控制后，铣削加工颤振频率大幅度下降，并趋于稳定，滚子轴承表面振纹显著减少。充分证实了本次所究所提方法具备较好的稳定性模糊控制效果。

3 结 语

滚子轴承是发动机主轴至关重要的部件，铣削加工稳定性控制是保障发动机性能稳定发挥的关键。为了满足滚子轴承的应用需求，对滚子轴承铣削加工稳定性模糊控制方法进行了研究。本次研究基于模糊集合理论设计了模糊PID控制器，实现了对滚子轴承铣削加工稳定性的模糊控制，降低了铣削加工颤振频率，减少了滚子轴承表面振纹，为滚子轴承铣削加工提供更有效的支撑。