双轴压应力作用下混凝土徐变特性研究*

荣 华 范兴朗 耿 岩 董 伟

(1.中冶建筑研究总院有限公司， 北京 100088； 2.中冶检测认证有限公司， 北京 100088；3.大连理工大学， 辽宁大连 116024)

预应力混凝土安全壳结构是核电厂最后一道安全屏障，确保其在服役过程中的设计功能至关重要。安全壳属于双向预应力体系，预应力钢筋沿混凝土结构竖向及环向施加预压作用，在预应力长期作用下混凝土沿两个受力轴方向均产生徐变变形。如何准确评估双向压应力作用下混凝土的徐变特性是安全壳结构预应力损失时变分析的关键，也是安全壳结构全寿期安全性评价的重要基础。

目前对单轴受压作用下混凝土徐变预测模型的研究开展比较充分，按照其建立思路，可以分为三类：第一类根据试验结果对持载过程中混凝土变形规律进行整体描述，如我国的JTG 3362—2018《公路钢筋混凝土及预应力桥涵设计规范》及美国AASHTO LRFD 2007标准等；第二类依据外部作用所产生的徐变机理不同，将其区分为基本徐变与干燥徐变，如欧洲模式规范CEB-FIB(MC 2010)及Bažant提出的B3[1]、B4[2]模型等；第三类根据卸载后混凝土的变形恢复规律将其区分为可恢复徐变和不可恢复徐变，如欧洲模式规范CEB-FIP(MC78)徐变模型及我国TB 1002.1—99《铁路桥涵设计基本规范》。需要说明的是，这些模型所考虑的影响因素及选用的计算参数各有特点，与试验结果的吻合也相差较大[3]。

对于双轴受压混凝土徐变特性的研究，由于机理的复杂性及试验操作困难，目前开展的研究非常有限。Liu等开展了早龄期混凝土双轴受压徐变试验，结果表明，双轴荷载在早期更易压实整个水泥凝胶骨架，促进水化，进而形成新的胶结物使裂缝闭合[4]。Benboudjema等的研究表明，单轴应力线性徐变条件下，混凝土徐变与施加的应力成正比，而双轴应力下测得的应力、应变的体积分量与偏差分量之间存在相同的线性关系[5]。柯敏勇等采用十字交叉梁开展了2种应力组合条件下的高强钢筋混凝土双轴徐变试验，结果表明双轴应力比对高强混凝土徐变影响较大，双轴压缩情况下的徐变变形小于相同应力单轴徐变变形[6]。高虎等的试验研究也证明了相同应力下双轴徐变和单轴徐变变形差别较大[7]。Kim等研究了多轴应力下不同强度混凝土的徐变特性，结果表明，随着混凝土强度的增加，初始荷载时的泊松比和组合应变的泊松比略有增加，体积徐变应变和偏差徐变应变分别与体积应力和偏差应力成线性比例[8]。由以上分析可知，已有的报道基本停留在对试验现象的描述与分析，缺乏适用性的双轴受压徐变预测模型。

基于此，本文开展了双轴受压应力状态下混凝土徐变特性研究。首先根据混凝土双轴受压徐变特点，提出了徐变泊松比模型并构造了泊松比影响矩阵。修正了B4徐变模型并给出了高效数值算法。最后通过文献[8-9]中单轴、双轴试验结果以及某安全壳结构对模型进行了验证。

1 混凝土双轴受压徐变模型

对于核电厂安全壳等筒状预应力混凝土结构，双向轴压徐变效应显著。目前对双轴不同应力比作用下的徐变变形规律研究尚不成熟，还缺少有效的模型对这一特性进行描述。宏观机理上，长期双轴受压下任一受力轴混凝土的变形由该轴受力产生的徐变变形及另一轴泊松效应变形决定，因此需要将这两部分作用分别量化。下面将分别对双轴受压下徐变泊松比模型及徐变变形模型进行分别阐述。

1.1 徐变泊松比模型

单轴受压条件下，徐变泊松比定义为非受力轴及受力轴的徐变量之比。根据已有文献的报道[10]，在双向轴压应力σ1、σ2组合作用下，不同应力方向的徐变泊松比与应力状态相关，本文采用式(1)计算受力轴1、2的徐变泊松比νc1,2与νc2,1：

式中：νc1,2为受力轴为2轴、非受力轴为1轴的徐变泊松比；νc2,1为受力轴为1轴、非受力轴为2轴的徐变泊松比；a、b和c均为与混凝土强度等级相关的材料常数。

按照二维弹性矩阵进一步定义徐变泊松比影响矩阵Cν：

(2)

1.2 二维双向受压徐变非线性本构模型

对于在时刻τ开始作用不变应力σ(τ)的混凝土构件，任意时刻t的总应变可以写为：

ε(t)=εσ(t)+εn(t)

(3a)

εn(t)=εa(t)+εs(t)+εT(t)

(3b)

式中：εσ(t)和εn(t)分别为混凝土荷载作用应变和非荷载因素应变；εs(t)和εT(t)分别为混凝土的收缩应变以及温度应变；εa(t)为混凝土的老化应变，指由于混凝土弹性模量随时间变化而产生的力学应变。

当混凝土构件单轴受压时，混凝土轴向总应变可以进一步写为：

(4)

式中：J(t,τ)为徐变函数，表示构件τ时刻施加单位荷载持荷至t时刻的应变；σ(τ)为τ时刻构件所受应力。

当混凝土双轴受压时，徐变函数与双轴应力状态相关。因此，受力轴i=1、2的应变可写为：

ε(t)i=Jbi(t,τ,σ1,σ2)·σ(t)i+

(5)

式中：Jbi(t,τ,σ1,σ2)为双轴压力下受力轴i的徐变函数，本文通过修正Bažant的B4模型徐变函数来表示[2]：

(6)

式中：E0为渐近弹性模量；f(σ1,σ2)为双轴压力对徐变函数的影响；Jb(t,τ)和Jd(t,τ)分别为基本徐变函数和干燥徐变函数，其计算式如下:

(7a)

式中：q2、q3、q4和q5分别为材料参数，可通过相关试验确定。

函数Q(t,τ)的表达式为：

(8)

式中：m和n分别为常数，可事先确定。

2 混凝土双轴受压徐变数值计算方法

由于式(5)为积分方程组，对于式(6)表达式的Jbi(t,τ,σ1,σ2)无法获得解析解，实际计算时应对其进行离散求解。目前比较通行的算法是率数值算法[11]，该算法的主要思想是采用Kelvin链模型来表征混凝土的黏弹性行为，即采用Dirichlet 级数的有限项和来近似表示混凝土的徐变函数，即：

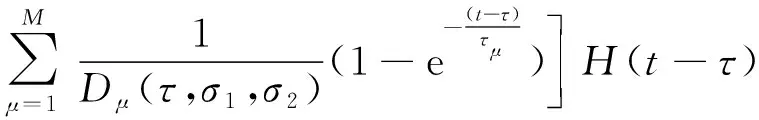
(9)

采用式(9)对徐变函数进行近似后，结合泊松效应的影响，可以构造出双轴压应力下混凝土徐变量计算算法。具体过程如下：

1)当t=t1时，内变量为σvμ,其中，μ=1,2，…，M置零；

3)徐变应变增量计算：

(11)

4)基于给定应变增量来计算应力增量：

(12)

5)更新应力：

σvμ,k+1=λμkΔσk+βμkσvμk

(13)

6)增大时间步，重复步骤2)～5)。

通过编制umat子程序，即可将上述算法集成于ABAQUS有限元平台。结合混凝土收缩模型以及钢束松弛模型，能够实现双向预压应力作用下安全壳结构变形时变演化分析。

3 数值验证

为了验证本文提出模型，将本文计算结果与文献中既有试验结果进行对比。算例1比较了双轴受压条件下混凝土徐变理论计算值与试验结果，验证模型在不同双轴压应力组合条件下的准确性。算例2比较了单轴高应力作用下理论计算值与试验结果，验证模型预测混凝土非线性徐变变形的可靠性。算例3通过在ABAQUS平台中集成本文所提混凝土徐变模型以及混凝土收缩模型和钢束松弛模型，对预应力安全壳结构进行预应力损失时变演化分析，验证本文材料徐变模型在分析结构响应中的有效性。

3.1 算例1

算例1数据来自文献[8]完成的系列多轴受压徐变试验。该试验共对3种混凝土强度等级的27个试件在密封条件下分别进行单轴、双轴和三轴受压试验。试件为边长200 mm的立方体试块。本文选取其中的CIII混凝土的部分双轴试验结果与理论计算结果进行对比。CIII混凝土强度fc为54.3 MPa，弹性模量为34 GPa。图1比较了双轴压值(σ1,σ2)分别为(0.22fc,0.07fc)以及(0.18fc,0.035fc)时的主轴ε1和次轴应变ε2的试验值与理论值。可以看出，理论计算结果和试验结果吻合良好，说明理论模型能够较好地反映不同双轴压组合情况下混凝土的徐变变形。

图1 不同双轴压组合混凝土徐变变形理论值与试验值比较Fig.1 Comparisons of theoretical and experimental creep strain under biaxial compression

3.2 算例2

算例2数据来自文献[9]完成的一系列混凝土圆柱体试件持续单轴受压试验。试件在浇筑完成后28 d开始持荷，荷载范围为(0.2～0.65)fc，其中fc为混凝土单轴抗压强度。计算中，混凝土弹性模量为21.5 GPa，泊松比为0.2，fc为47.5 MPa。图2比较了不同持续应力水平下的试验结果和理论计算结果。可以看出：理论计算结果在各应力水平下均与试验结果吻合良好。图3表示不同应力水平下混凝土最大应变值，可以看出，在高应力水平下，试件变形表现出明显的非线性趋势，理论计算结果能够较好地反映出高应力水平下非线性徐变行为。

图2 不同应力水平下试验与理论计算结果对比Fig.2 Comparisons of theoretical and experimental creep strain under different uniaxial load levels

图3 不同应力水平下混凝土最大应变试验结果Fig.3 Maximum strain of specimens under different stress levels

3.3 算例3

将上述开发的经过验证的徐变模型用于某实际安全壳结构分析，采用ABAQUS有限元分析软件进行数值计算。安全壳筒身内径11.25 m，壁厚0.30 m，高度为15.98 m，穹顶厚度为0.67 m。安全壳结构内共设置了3种型式的预应力钢束：1)γ型预应力钢束(V)；2)筒身竖向垂直预应力钢束(V)；3)筒身环向水平预应力钢束(H)。γ型预应力钢束两端分别锚固在穹顶环梁和共用筏板基础上，共计100束；竖向垂直预应力钢束两端分别锚固在穹顶环梁和共用筏板基础上，共计44束；环向水平预应力钢束经扶壁柱一侧起环绕筒身一周后锚固在同一扶壁柱对侧，相邻的两束水平预应力钢束锚固端所在扶壁柱分别位于133°、313°，呈交错状布置，共计98束。水平预应力筋截面面积为56×10-5m2，竖向和γ型预应力筋截面面积为60×10-5m2。按照安全壳图纸进行精细化建模，模型(图4)包含混凝土壳体、钢内衬、基础、廊道、预应力钢筋、预应力施加端口的垫块及3个闸门(1个设备闸门、2个人员闸门)。混凝土、垫块均采用Solid 45单元，预应力钢筋采用Truss单元，单元长度控制在0.1 m左右。

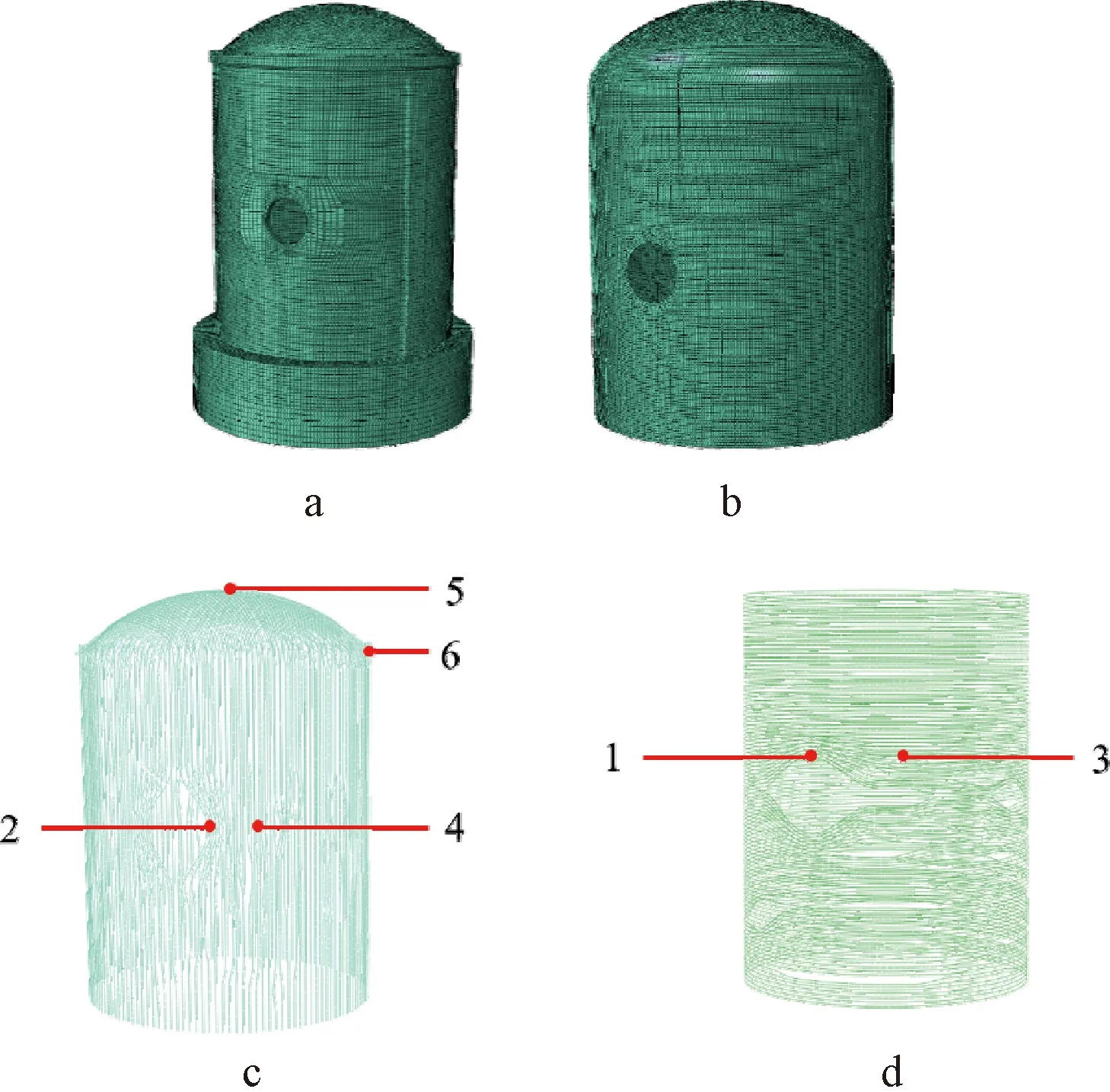
a—安全壳混凝土； b—内衬； c—竖向及γ钢筋； d—水平钢筋。1～6为钢束位置。图4 有限元模型Fig.4 FEA model

计算中，除了混凝土徐变分析采用本文提出的徐变本构模型外，同时还考虑了混凝土的收缩变形，采用Bazant提出的B4收缩模型进行模拟。计算时，周围环境湿度为85%。预应力钢筋采用基于黏塑性理论的钢束松弛模型进行模拟，通过Embedded方式嵌入混凝土内部，不考虑钢束与混凝土之间的黏结滑移效应，预应力效应利用降温法进行模拟，预应力钢筋的端部与垫块利用绑定约束进行耦合，垫块与混凝土表面采用绑定约束进行连接。安全壳筒身及穹顶采用C60混凝土，底板采用C40混凝土，垫块采用Q235钢，预应力钢束采用1 860 MPa级钢绞线，材料参数见表1。

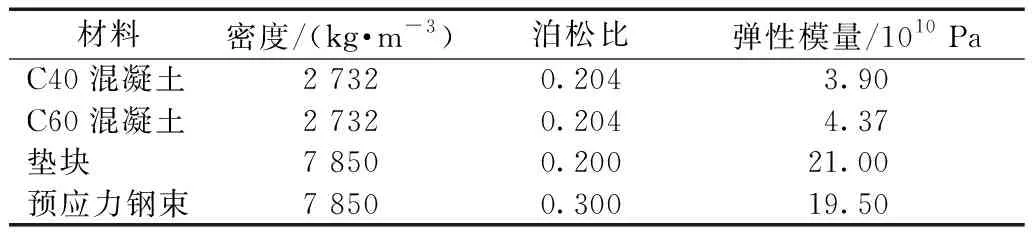
表1 数值计算材料参数Table 1 Material parameters for numerical calculation

结构施加预应力后，考虑混凝土收缩、徐变对预应力损失的影响，在预应力加载1 000 d后，不同位置钢束的预应力损失情况见图5。从整体上讲，1 000 d内的预应力损失最大不超过70 MPa。具体来说，预应力损失最多为闸门洞口附近的水平钢束(69.9 MPa)，预应力损失最少处为筒身连续处的竖向钢束(23.6 MPa)，穹顶钢束中部和端部的损失分别为45.6 MPa和53.5 MPa。已有文献报道，实测安全壳结构的预应力损失值远远小于目前既有的预应力损失计算方法的计算值，既有方法计算结果严重偏保守[12-13]。通常情况下，预应力主要损失出现在服役前5年。本文计算结果表明，各个部位预应力损失值在前3年均小于张拉值的8%，这与相关文献报道趋势相符，说明了本文预应力损失分析方法的合理性。

a—洞口附近钢束预应力时变损失； b—筒身连续处钢束预应力时变损失； c—穹顶钢束预应力时变损失。图5 预应力加载1 000 d后预应力钢束时变损失情况Fig.5 Time-dependent prestress loss of prestressed tendons after 1 000 days of prestressing

需要指出的是，在对实际安全壳结构预应力损失进行评价时，还需要对预应力损失的不确定性进行量化。由于不确定输入参数较多，进行不确定性量化分析时需要消耗大量的计算资源。一个相对好的解决方案是利用采样技术和有限元仿真构造一个高精度自适应kriging等代模型，然后再利用监测系统数据对该等代模型参数进行识别并实时对等代模型进行更新。在等代模型基础上进行不确定性量化分析，从而大大提高了分析效率。该方法已经集成于本文作者开发的预应力安全壳结构性能评价分析平台，限于篇幅，此处不进一步展开。

4 结束语

预应力安全壳结构混凝土长期处于双向受压高应力状态。混凝土双轴受压徐变变形特征与单轴受压差别较大，目前大多数基于单轴受压徐变试验的徐变模型不能准确预测混凝土双轴受压徐变变形，从而不能精确预测安全壳结构预应力损失时变行为。研究提出了徐变泊松比模型，发展了应力状态下混凝土徐变非线性模型并构造了高效算法。文中模型与文献试验结果吻合良好，能够准确反映双向受压徐变变形特征和高应力状态的非线性特征，能够用于预测安全壳结构等双向受压混凝土结构的徐变变形特征。