风力机塔架-叶片耦合结构与单个叶片模态参数对比研究*

李志军，董 彬，马江波，李 刚

(1.西安工业大学 建筑工程学院，西安 710021；2.西安工业大学 机电工程学院，西安 710021)

随着我国风电技术的快速发展，到2020年，我国的风电新增装机容量在全球排名第一[1]。风力机主要由塔架、机舱、叶片、轮毂等结构组成。其中叶片是获取风能的核心结构。随着风力机大型化，叶片的长度越来越大，从而呈现刚度低、阻尼弱的特点[2]。叶片应具有更加良好的翼型结构、材料和加工工艺，保证叶片具有足够的结构刚度和韧性，以便提高风能利用率以及承受更大的外部载荷。否则，因工作环境因素产生的叶片振动会导致叶片开裂或者折翼，更严重时会导致叶片折断报废，造成倒塌[3]。

文献[4]对单个叶片进行了模态分析和风致振动控制分析，仿真结果有良好的控制效果，但研究中没有考虑机舱、塔架对叶片振动的影响。文献[5]对5 MW风力机单个叶片基于叶片根部固定进行了动力响应分析，通过加载不同工况的风荷载，结果表明随着风速的增大，叶片根部的应力是增大的，但是叶片根部按理想的固定端约束处理会引起一定的计算误差。文献[6]对风力机叶片平面内的振动进行了主动控制研究，采用欧拉-拉格朗日法计算了塔架对叶片的耦合结构的模态分析，随后进行了振动控制，但未考虑塔架对叶片振动的影响。文献[7]对风力机风轮的气动特性以及风力机组振动特性进行了研究，考虑了多个叶片结构，但没有考虑塔架对叶轮的影响。文献[8]同样研究了叶轮的流固耦合仿真分析，通过ANSYS WorkBench软件搭建了叶轮流固耦合模型，通过加载风荷载，对风轮的整体稳定性进行研究，但并未结合实际工况研究塔架、机舱对叶片振动的影响。文献[9]对大型风力机塔架进行了风-沙工况响应分析，主要探究了风力机塔架叶片耦合结构在风沙共同作用下的动力学响应，对塔架叶片耦合结构的模态分析缺少研究。文献[10]研究了风力机塔架的振动特性，分别对风力机停机和运行两种工况进行了仿真分析，结果表明风力机的运行对塔架的振动频率有一定的影响。同样是仅对塔架进行了振动响应分析，没有考虑叶片与塔架的耦合作用。考虑到风力机组工作环境的复杂程度，传统的对单个叶片进行振动分析相比实际工况下的叶片振动有较为明显的差距，忽略了对于风力机本身模态的研究。

为获得复杂工况下的叶片风致振动响应，需要对风力机进行整体结构建模，以考虑塔架、机舱、轮毂对叶片振动的影响，文中建立了塔架-叶片-机舱的整体三维模型和动力学模型。将机舱底部固定在塔架上端，将叶片固定在轮毂上，然后通过机舱与塔架连接，按产品的实际参数建模，从而实现仿真分析过程中考虑塔架对叶片振动的耦合作用，并对单个叶片和塔架-叶片耦合结构两种不同的模型进行模态分析，为风力机叶片振动控制技术发展提出依据。

1 风力机塔架-叶片耦合模型

1.1 风力机参数选取

文中采用目前技术成熟的NREL-5 MW涡轮风力机作为研究对象，其机组性能和结构参数[11-12]具体见表1。

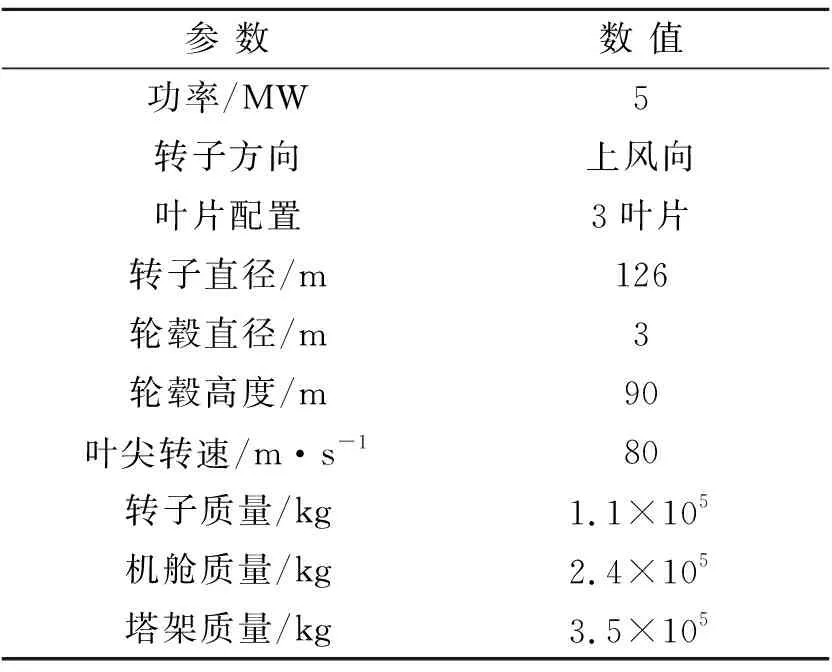
表1 NREL-5 MW风力机参数Tab.1 Structural parameters of the NREL-5 MW wind turbine

1.2 单个叶片三维模型

通过NREL-5 MW涡轮风力机的性能参数，计算可得到叶片各翼型参数见表2。对于Cylinder1，DU40_A17系列以及NACA64_A17翼型坐标，可通过翼型设计软件来对叶片翼型截面的二维坐标进行查询，但是二维坐标难以完整表述叶片的三维形状，因此，需要将二维坐标转换成三维坐标去进行三维建模。坐标变换法正是通过已有的每个叶片的弦长和扭矩，将二维坐标数据进行坐标变换计算，得到相应的三维坐标，将三维坐标保存为.bat文件，导入到Solidworks中，最终生成叶片三维模型，再对边缘接缝处进行处理，具体操作步骤如下：通过坐标变换法得到叶片的截面三维空间坐标，将其保存为.bat文件，.bat文件可以直接加载进Solidworks软件中。通过一系列的草图绘制，得到了叶片各截面的草图，通过曲线拟合建立完整的叶片三维模型。

以文中采用的5 MW风力机叶片为例，其额定功率设计P=5 MW，叶片截面弦长等参数见表2，将从profili中获取的多种翼型二维坐标按照相应的截面在Solidworks中绘制草图，通过曲线自动将各截面端部依次连接起来，从而完成翼型图的绘制，最终完成叶片模型的建立。叶片模型具体如图1所示。

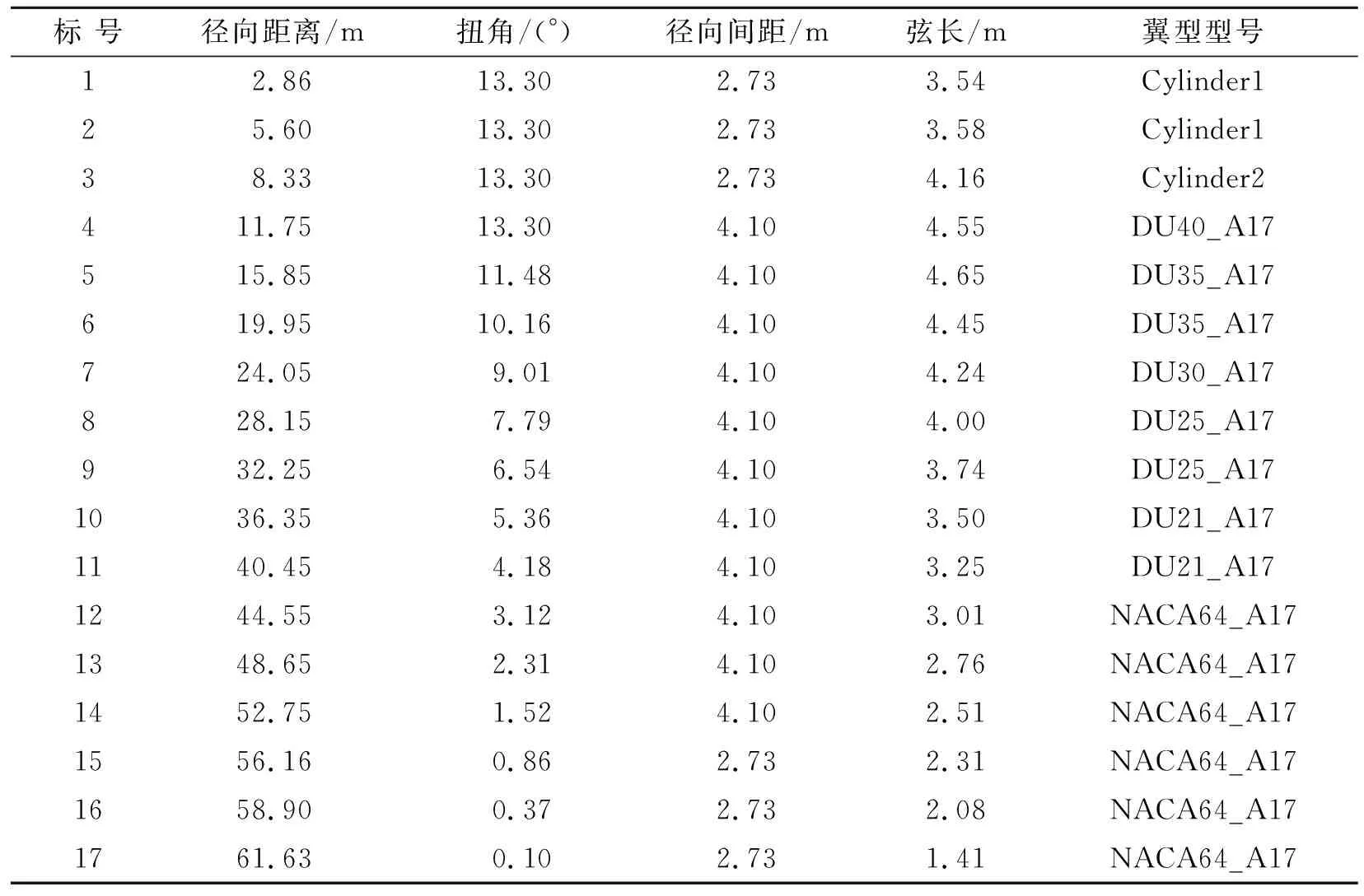
表2 NREL-5 MW风力机叶片结构参数Tab.2 Structural parameters of the NREL-5 MW wind turbine blades

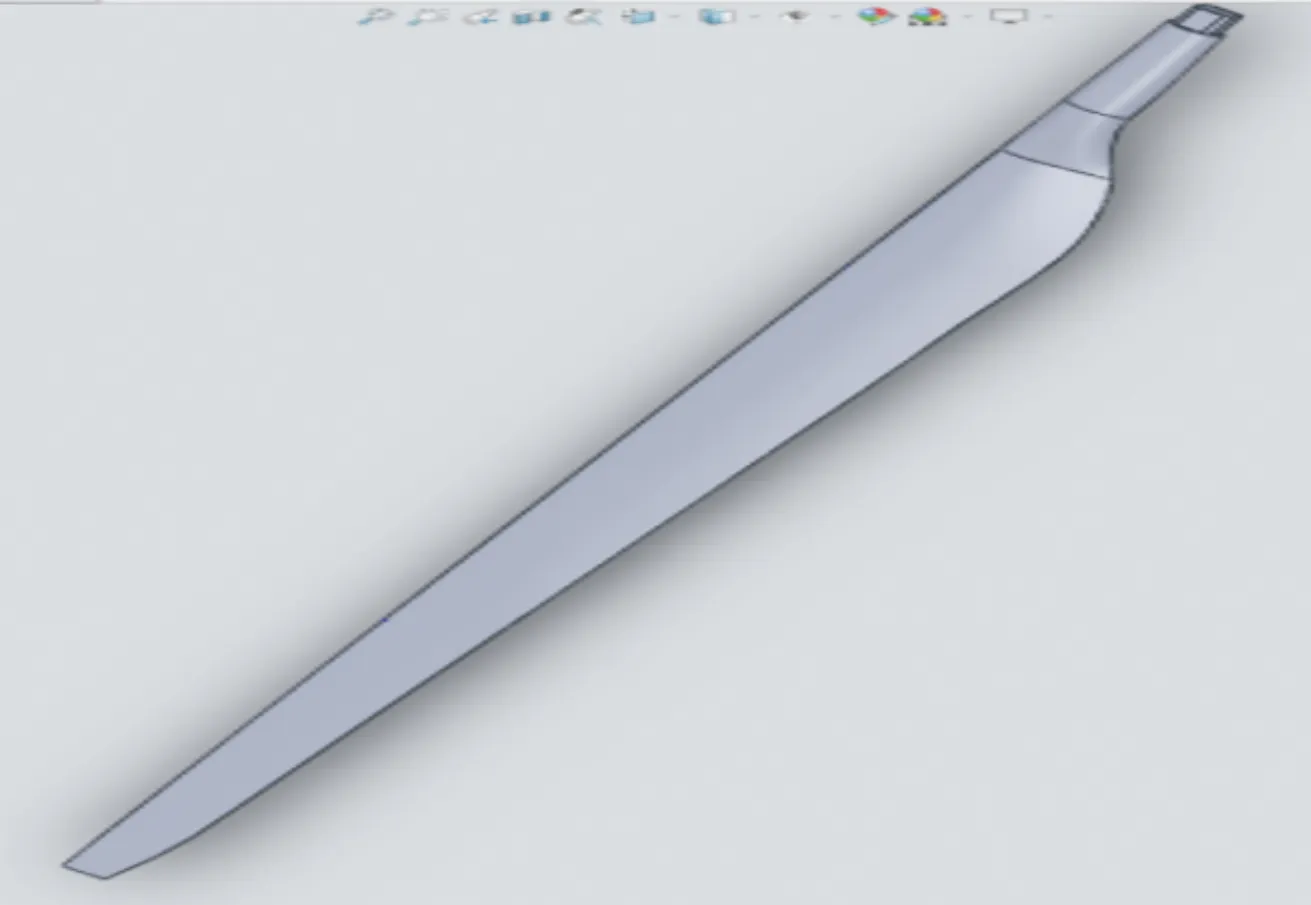
图1 风力机叶片三维模型Fig.1 Three-dimensional model of a wind turbine blade

叶片结构具体其根部截面最大，叶尖处截面最小，中间段逐渐变小，从结构上看，叶片的叶尖附近承载能力较小，振动产生的位移比较大。

1.3 塔架-叶片耦合三维模型

NREL-5 MW风力机的塔架性能主要取决于安装转子和机舱等的支撑结构，支撑结构的类型取决于安装地点，其属性参数主要有土壤类型、风力等级等参数来确定。文中选取的5 MW风力机的塔架、机舱、轮毂参数具体见表3。

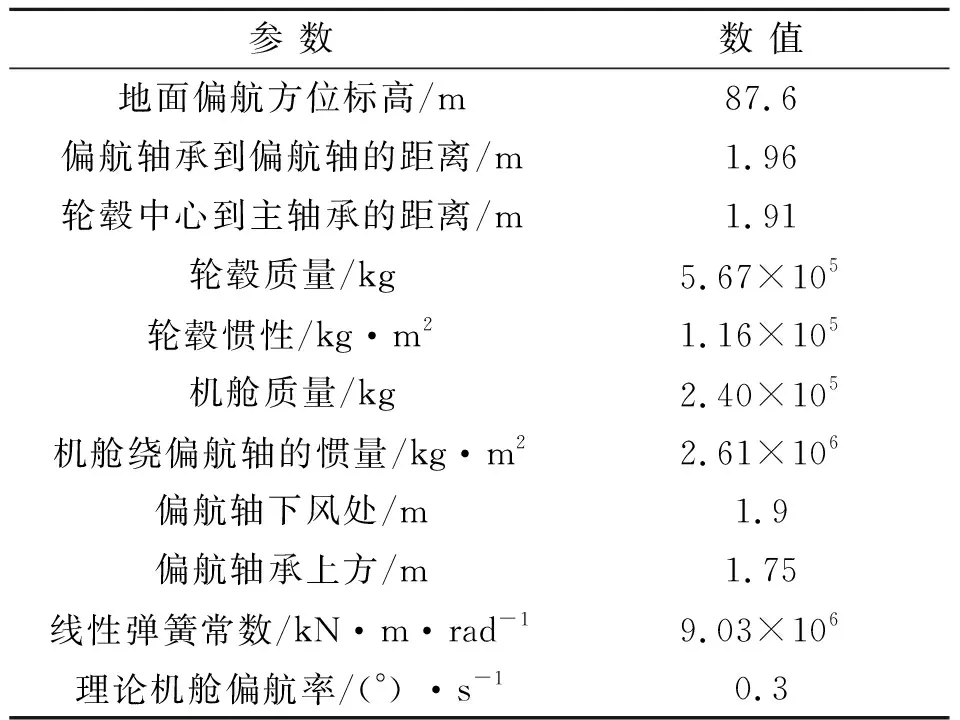
表3 机舱和轮毂参数Tab.3 Parameters of the nacelle and the hub

根据上述风力机各零部件的结构参数，在Solidworks三维建模软件中建立并装配风力机塔架-叶片耦合结构，具体如图2所示。

图2 风力机塔架-叶片耦合结构三维模型Fig.2 Three-dimensional model of the wind turbine tower-blade coupled structure

1.4 动力学模型

针对风力机叶片的振动问题，采用假设模态法，基于拉格朗日方程通过系统的动能、势能和一般荷载建立塔架-叶片耦合运动模型。动力学低阶矩阵微分方程如式(1)所示[13-14]。

(1)

式中：q={q1,in,q2,in,q3,in,qn,in}T为位移矢量；M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；Ql为风荷载；Qg为重力荷载；Um为控制力。单个叶片质量矩阵[15]为

(2)

单个叶片阻尼矩阵[15]为

(3)

单个叶片刚度矩阵[15]为

(4)

式中：y为叶片划分为n个单元中的第y个微单元。基于模态空间，单个叶片质量可以表示为

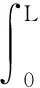
(5)

式中：μ(x)为叶片距叶根x处的单位质量函数。叶片面内振动一阶、二阶模态质量分别为

(6)

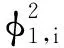
(7)

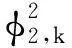
Mtj,h=3m0+Mjc+mtj,h。

(8)

塔架前后振动耦合结构总等效质量为

Mtjf=3m0+Mjc+mtjf,1。

(9)

风力机塔架-叶片耦合结构的质量[16-17]为

(10)

式中：O为2维零矩阵；M2=diag(m1,21,m2,21)为叶片模态质量矩阵；Mtj=diag(Mtj1,Mtjf1)为塔架模态质量矩阵；Mjφ=diag(Mj11,Mj12)为叶片与塔架耦合模态质量矩阵；其中Mj11=cos(φj)m1,1i,Mj12=m2,11;φj为叶片在t时刻的偏转角度。

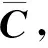
(11)

Cjg=diag[cb,cb,cb,c4],

(12)

式中，cb=diag(c1,c2),c4=diag(ctj,ctjf);

(13)

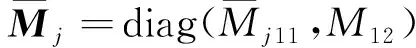
(14)

j=1,2,3,

式中：K1(ωr)=k1,21;K2(ωr)=k2,21;Kio=kio,11;K4=diag(Ktj,Ktjf)

式中：k1,21为叶片面内弹性重力及离心力导致的刚度；k2,21为叶片面外弹性重力及离心力导致的刚度；kio,11为叶片面内与面外耦合导致的刚度。

2 模态分析

2.1 有限元分析模型

1) 导入三维模型。Solidworks建模完成后保存的文件格式为.SLDPRT文件，通用有限元软件可以直接打开.SLDPRT文件，在菜单栏中选择要分析的类型，选择要分析的模型单击确定，即可载入要分析的三维模型，在Geometry工作空间中单击Generate进行模型生成[16]，生成的模型如图3所示。

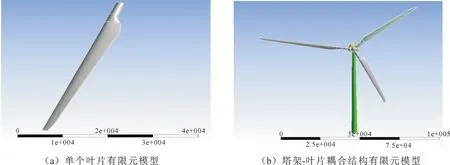
图3 导入有限元分析软件中的模型Fig.3 Finite element models

考虑叶片平面内外的模态分析，可得出耦合结构的第1，2阶叶片面内面外的振型函数为

φ1,i(x)=-0.6923x6+1.3754x5-3.5963x4+

2.5421x3+0.3549x2

φ2,i(x)=-2.3855x6+4.8723x5-3.38528x4+

1.7102x3+0.0623x2

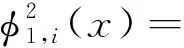
1.7528x3+1.3759x2

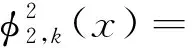
3.1796x4+0.6879x2

2) 基本设置。结构构件的材料、密度、弹性模量及泊松比是形成结构有限元模型的基础物理参数，各构件单元类型是影响结构模型动力特性的重要参数。主要构件采用的材料及物理参数见表4。

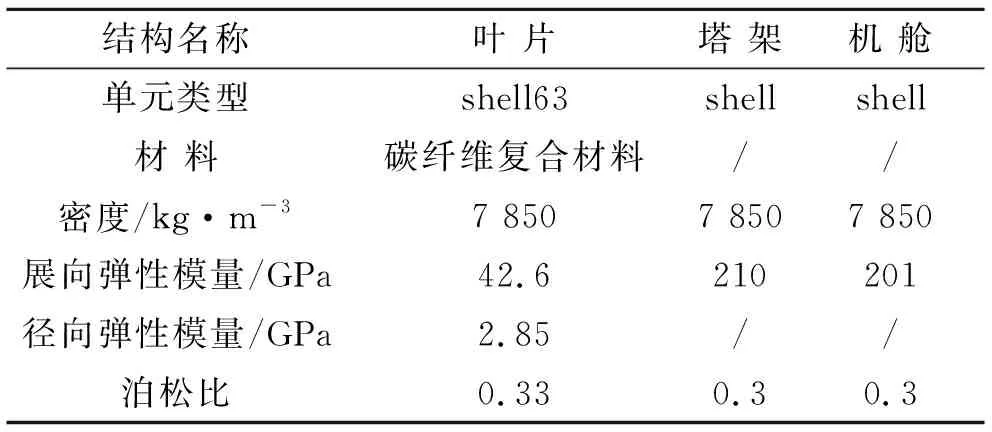
表4 结构材料与物理参数Tab.4 Material and physical parameters of each structural member

3) 塔架-叶片的网格划分及施加约束。设置好各部分结构材料参数后，对模型进行网格划分以及施加约束。为保证结构模态分析的精确性，文中对叶片划分网格时选用自适应网络来进行划分。

风力机叶片根部固定于轮毂上，设置水平和扭转约束；轮毂连接轴安装在机舱端部，设置水平约束；舱底部固定于塔架顶部，设置水平约束和扭转约束。

2.2 数值模拟及分析

大型风力机为避免发生共振，要避免结构主要模态频率接近风载主要频率。对单个叶片和考虑塔架耦合作用的叶片进行模态分析，计算出两种模型的主要模态频率和振型图，风力机叶片振动的能量主要集中在前6阶振型内，因此选取前6阶模态频率和振型进行研究，模态频率具体数值见表5，振型如图4和图5。

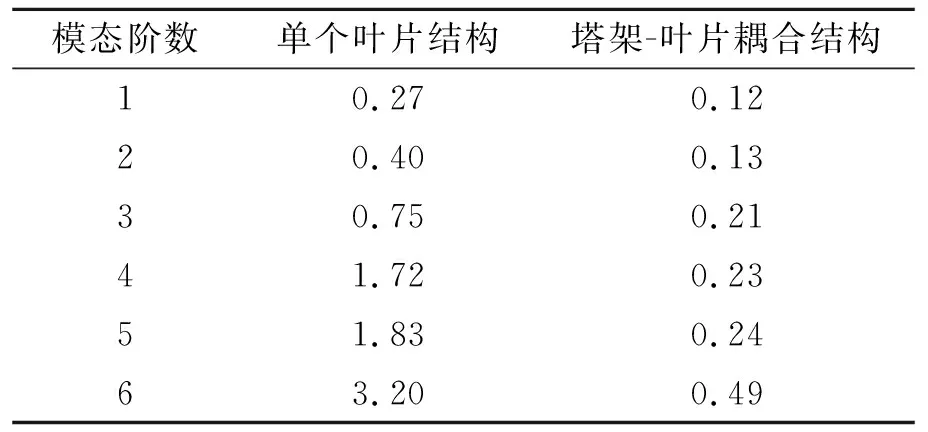
表5 单个叶片和塔架-叶片的耦合结构前6阶模态频率分析Tab.5 The first six order modal frequencies of the single blade structure and the tower-blade coupled structure

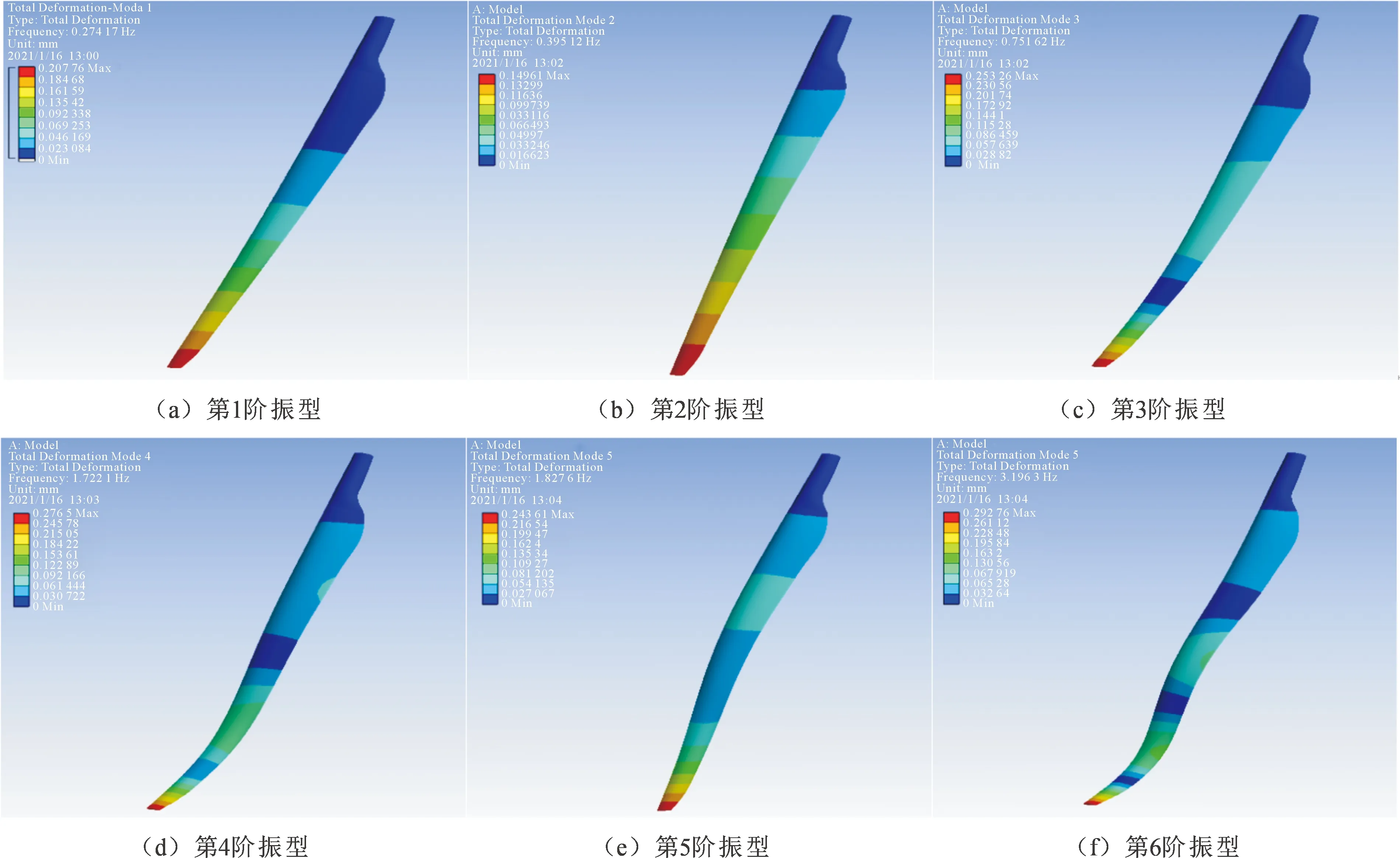
图4 单个叶片结构前6阶振型图Fig.4 The first six vibration modes of a single blade

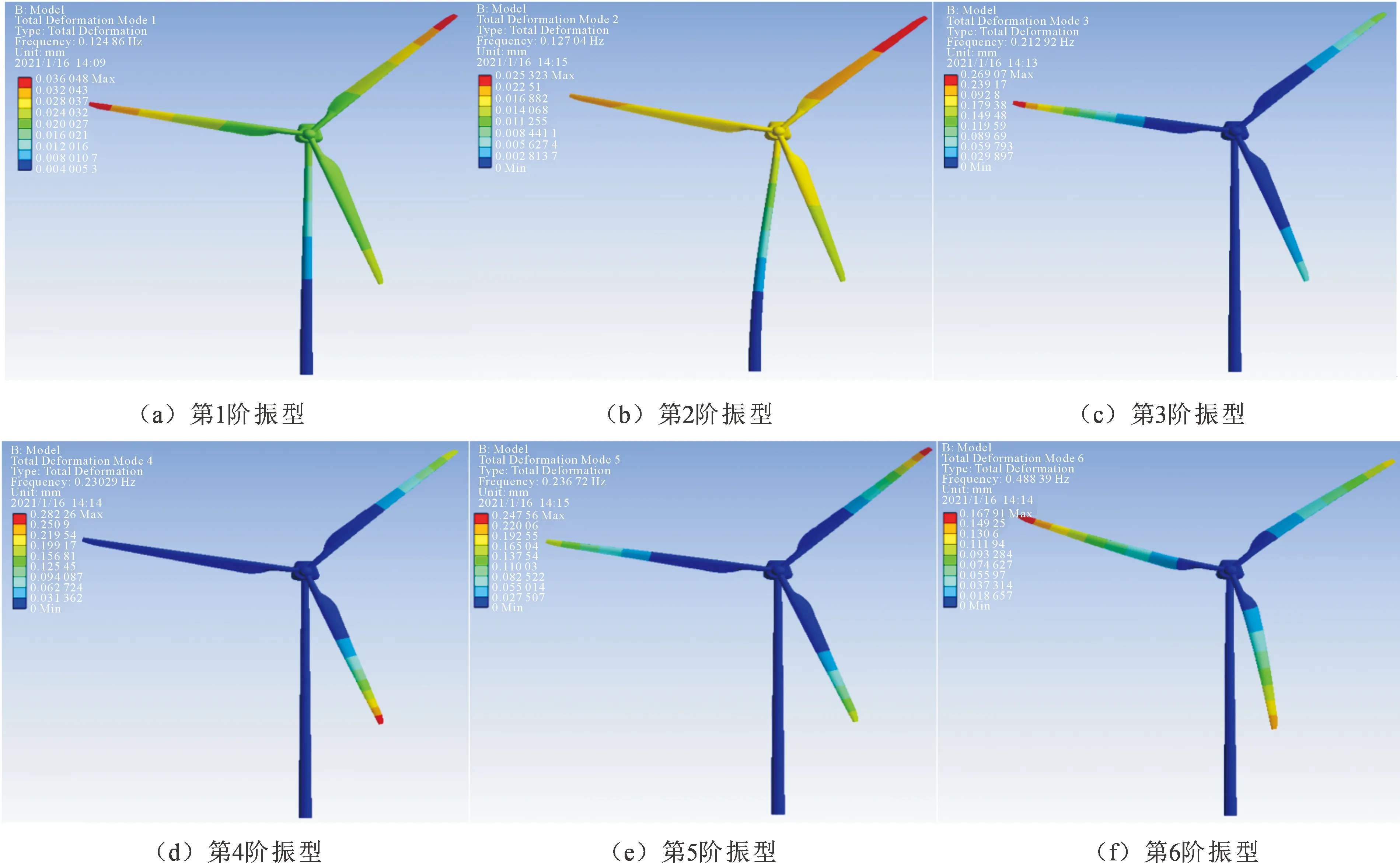
图5 风力机塔架-叶片耦合结构前6阶振型图Fig.5 The first six order vibration mode of the tower-blade coupled structure

由表5可知，对于单个叶片和塔架-叶片耦合结构模型，对比这两组固有频率可以得出：塔架-叶片耦合结构相比于单个叶片的固有频率在第一阶模态时只有单个叶片的44.44%，在第二阶模态时只有单个叶片的32.50%，在第三阶模态时只有单个叶片的28.00%，在第四阶模态时只有单个叶片的13.37%，在第五阶模态时只有单个叶片的13.11%，在第6阶模态时只有单个叶片的15.31%。

由图4对单个叶片的前6阶振型分析可知，单个叶片在前6阶模态中主要以挥舞和摆振两种振型为主，扭转振型次之，仅发生在第6阶模态中，但从单个叶片的前6阶振动形式来看，主要振动形式还是以平面内振动和平面外振动为主。由单个叶片振型图可知，单个叶片的模态振动最大位移集中发生在叶片的尖部，到叶片尖部顶端距离约是叶片总长度的20%。

经过对风力机塔架-叶片耦合结构前6阶振型图5进行分析，耦合结构的叶片的第1，第2阶模态为挥舞振动，第3，第4阶模态为摆振，第5，第6阶为扭转振动。由振型图可知，耦合结构叶片的模态位移发生最大处集中在叶片的尖部。

通过对表5、图4和图5的对比分析可知，单个叶片和风力机塔架-叶片耦合结构中叶片在前6阶的模态振型有差异。考虑塔架等结构对叶片的影响，叶片出现挥舞振动的模态阶数要小；但单个叶片和风力机塔架-叶片耦合结构的叶片模态振动位移最大处基本一致，这说明耦合结构对叶片结构的薄弱部位不产生影响。

从模态频率来看，考虑风力机塔架-叶片耦合结构时，风力机叶片的振动频率比只考虑单个叶片振动的固有频率要低，考虑到风谱频率主要集中在0～1 Hz的低频区，1～10 Hz也有一定的比例，这表明在实际工作环境中，风力机塔基-叶片耦合结构中的叶片更容易与风产生共振，因此考虑风力机塔架-叶片耦合结构对风力机叶片的振动是非常有必要的。

从振型图来看，叶片发生扭转振动的模态阶数提前了，这说明风力机塔架-叶片耦合作用会导致叶片在工作环境中更容易发生最不利振动形式，导致叶片损坏等情况。进而说明考虑风力机塔架-叶片耦合结构对风力机叶片的振动是非常有必要的。

3 结 论

1) 仿真结果表明，单个叶片的固有频率在一阶时最小为0.27 Hz，二阶为0.4 Hz，三阶为0.75 Hz，四阶为1.72 Hz，五阶为1.83 Hz，在六阶时最大为3.2 Hz；塔架-叶片耦合结构的叶片固有频率同样在一阶最小为0.12 Hz，二阶为0.13 Hz，三阶为0.21 Hz，四阶为0.23 Hz，五阶为0.24 Hz，在六阶最大为0.49 Hz。塔架-叶片耦合结构的叶片固有频率相比单个叶片的固有频率在一阶时减小55.55%，在二阶时减小67.5%，在三阶时减小72%，在四阶时减小86.63%，在五阶时减小86.89%，在六阶时减小84.69%。

2) 两种模型的振型图表明，叶片的振动位移最大处均在叶片的前端，两种工况下叶片在前6阶模态振型图中均以平面内的摆振和平面外的挥舞振动为主要振动形式。其中单个叶片在两种工况下第1，2阶模态为挥舞振动，第3，4阶模态为摆振，第6阶模态为扭转振动；第5阶模态略有不同。

3) 综合考虑，由于风荷载的频率较低，塔架与叶片的耦合会导致叶片的固有频率降低，叶片运行时会更容易产生风致振动。因此，在对叶片进行振动响应分析时，需要考虑塔架、机舱、轮毂对叶片风致振动产生的耦合作用，从风力机整体建模分析叶片的振动和振动控制。