灵巧型大孔径四反星敏感器镜头设计*

王永宪，朱俊青，张瑞平,2

(1.中国科学院长春光学精密机械与物理研究所 空间光学研究一部·长春·130033；2.中国科学院大学·北京·100049)

0 引 言

星敏感器是组成高精度姿态轨道控制系统的重要单机，其以星图中恒星的位置作为参考基准，确定飞行器自身的姿轨控参数，具有体积灵巧、定位精度高、自主度高、无累积误差、功耗低等优点，是目前所有姿轨控导航系统中精度和稳定性最高的，其长时间连续工作依然可以保障导航精度满足角秒量级[1-5]。

星敏感器镜头是星敏感器的前端组件，是星敏感器的关键部分，其对恒星的成像质量直接决定了星敏感器整机的测量精度。捕捉到足够的恒星数量是星敏感器正常工作的前提，恒星发光微弱，需要光学镜头具有大相对孔径、宽光谱范围和高杂散光抑制性能，以此来发现内视场更多的恒星作为飞船定姿的参考基准。传统的星敏镜头多采用双高斯型全透射的光学结构，这种结构以孔径光阑为中心，前后光学元件的数量和光角度成对称分布，能够很好地校正系统的畸变和色差。复杂化的双高斯光学结构会在孔径光阑后加入一片到两片正光角度透镜，增强系统的像差平衡能力，提高镜头的成像性能。但随着视场和相对孔径的增加，为了校正系统的轴外像散和畸变，双高斯结构会变得非常复杂，造成系统的体积增大、质量增加，并同时为后期镜头的装配增加难度，并且透射系统的工作波段还受限于光学材料的选择，在力热性能方面也增添了一些限制。为了在保证系统像差校正能力的前提下，增加星敏镜头的集光面积，出现了折反混合的星敏镜头。折反混合的镜头多以卡塞格林结构作为初始结构，并在后面加入了2～3片校正镜组，以克服卡塞格林系统作为星敏镜头视场小、轴外慧差无法校正的问题。卡式折反混合系统在一定程度上增加了系统的集光面积，但由于其中心遮拦的存在，系统的集光面积与直径50mm以下的纯透射星敏镜头相比无明显优势，包络尺寸上系统经过一次折反，在一定程度上压缩了镜头的体积，但后端校正镜组为星敏镜头的装配增加了难度[6-9]。

近几年来，出现了全反射式的星敏镜头。全反射式的星敏镜头中无透射光学元件，彻底消除了色差对镜头性能的影响。得益于镀膜技术的发展，全反射式星敏能够实现较宽的工作谱段范围；得益于大口径非球面加工技术的发展，设计者能够利用非球面甚至自由曲面面形增加全反射系统的优化自由度，提升镜头的像差平衡能力，并且更容易实现大集光面积，提升星敏整机的探测能力[10-13]。

基于全反射星敏的诸多优势，设计得到了一种灵巧型、大相对孔径四反星敏感器光学系统。光学系统在卡式结构的基础上，增加了两片非球面反射镜，而非球面的使用压缩了轴向尺寸，扩展了视场，同时提升了镜头轴外像差的校正能力。通过全局优化将系统的主镜和三镜设计为一块反射镜，降低了加工成本和装配难度。系统能够配合适当的机械结构，有效降低空间环境温度变化、地面安装误差等造成的像面离焦对弥散斑质心位置计算的影响。镜头具有内、外两层遮光罩，能够很好地抑制轴外3°～42°范围的杂散光，保障整机在工作时像面具有良好的信噪比和灰度层次。

1 参数分析

星敏镜头被用于对远处的恒星进行成像观测，属于点目标探测光学系统，最主要的性能指标就是镜头的探测能力，其探测能力与恒星目标本身的尺寸、亮度以及光学系统的口径及探测器的性能有关，以7.5等星、信噪比3、弥散斑直径20μm计算，得到积分时间与镜头口径(集光面积)的关系曲线如图1所示，同时得到信噪比与积分时间的关系曲线如图2所示。

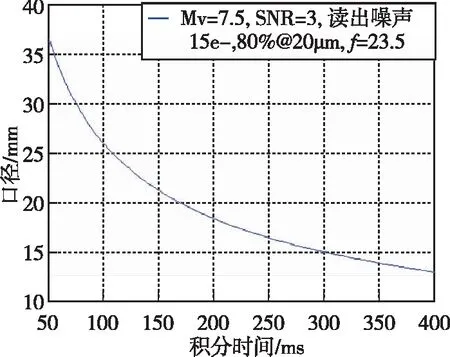
图1 积分时间与镜头口径关系曲线Fig.1 Curve of integration time and aperture

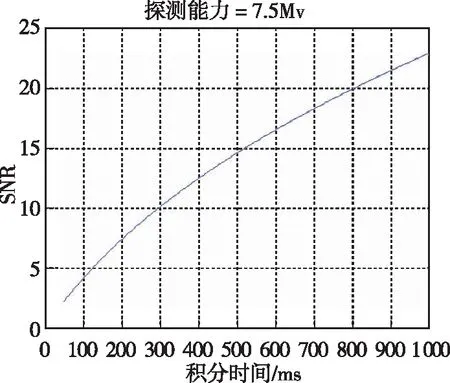
图2 信噪比与积分时间关系曲线Fig.2 Curve of integration time and SNR

根据对信噪比、积分时间和镜头口径的分析，可以得到在图像探测器一定时，星敏镜头的集光面积越大，光学传递函数越高，系统透过率越高，可探测的星等就越高，需要的积分时间就越短。相对来说，系统也就越复杂。在考虑了目前现有的光学元件加工、检测以及机械结构设计装配能力等综合因素的条件下，拟定四反星敏镜头的设计指标如表1所示。

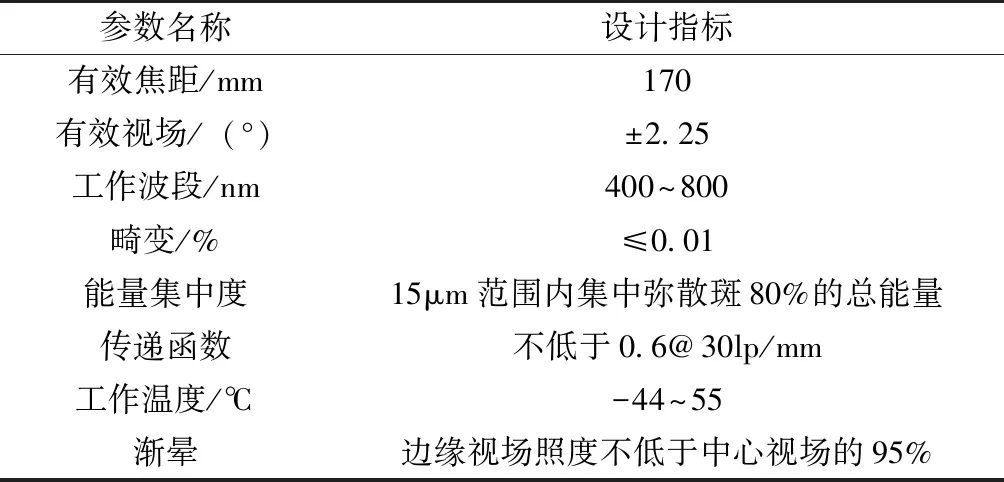
表1 星敏感器光学镜头设计指标

2 设计与优化

2.1 初始结构选择

设计方案是在卡式结构的基础上增加了三镜和四镜，并加入非球面校正系统的像差，使系统最终达到预计目标。因此，设计及优化过程主要分3个过程，首先需要计算得到合适的卡式结构作为初始结构，然后以弥散斑及传递函数作为评价标准，建立评价函数进行优化，最后加入边界条件进行全局优化。

设计初期根据像差理论[14-15]，可以得到完全消球差和慧差的同轴两反中，主镜二次系数和次镜二次系数的表达式如下

式中，e1为主镜二次系数，α为主镜遮拦比，β为主镜放大率；e2为次镜二次系数，α为次镜遮拦比，β为次镜放大率。

根据以往的设计，选择主、次镜遮拦比为0.377，得到主、次镜的二次系数分别为-1和10.766；根据目标焦距分配主、次镜光焦度，设定主镜曲率为191.82mm；根据主、次镜焦距的代数关系，可以计算得到次镜的曲率为153.73mm，同时得到主、次镜间隔为60mm。至此得到了镜头的初始结构，如图3所示。

图3 初始结构二维光路图Fig.3 2D layout of initial structure

2.2 星敏镜头的优化

星敏镜头对于成像弥散斑形状没有明确定义，但星敏镜头的弥散斑需要便于后期的质心提取。因此，从其图像处理算法来看，慧差小、像散小、圆度高、成旋转对称的弥散斑，对整机的功能实现和性能提升更有利。

在初始结构的基础上，为了进一步压缩轴向距离，扩大视场，提升系统性能，在初始结构中加入三镜和四镜，同时以各个反射镜的非球面系数作为变量，以系统的弥散斑和传递函数作为评价标准进行本地优化和全局优化。经过设计实践，最终得到了弥散斑能量集中度高、圆度高的四反光学系统，如图4所示。

图4 四反系统光路图Fig.4 The four-system optical path diagram

3 性能及公差分析

3.1 性能分析

经优化设计后的四反射式星敏感器光学系统为像方远心结构，通过主镜及次镜遮拦比可以计算出系统有效入瞳直径为52mm，极大提高了观察视场内暗星的能力。系统场曲及畸变如图5所示，系统的场曲优于200μm，畸变优于0.01%。点列图如图6所示，全视场弥散斑RMS直径在5～13μm之间。其弥散圆能量分布如图7所示，全视场下80%弥散圆能量集中在15μm以内。

星敏镜头采用全反射设计，其中无透射材料，无垂轴色差与倍率色差，能够实现全波段质心位置无偏差，本星敏感器弥散圆能量质心位置统计如表2所示。

图8所示为星敏镜头的传递函数曲线，全视场传递函数曲线在35lp/mm处大于0.6，并且接近衍射极限，子午和弧矢方向传递函数接近。

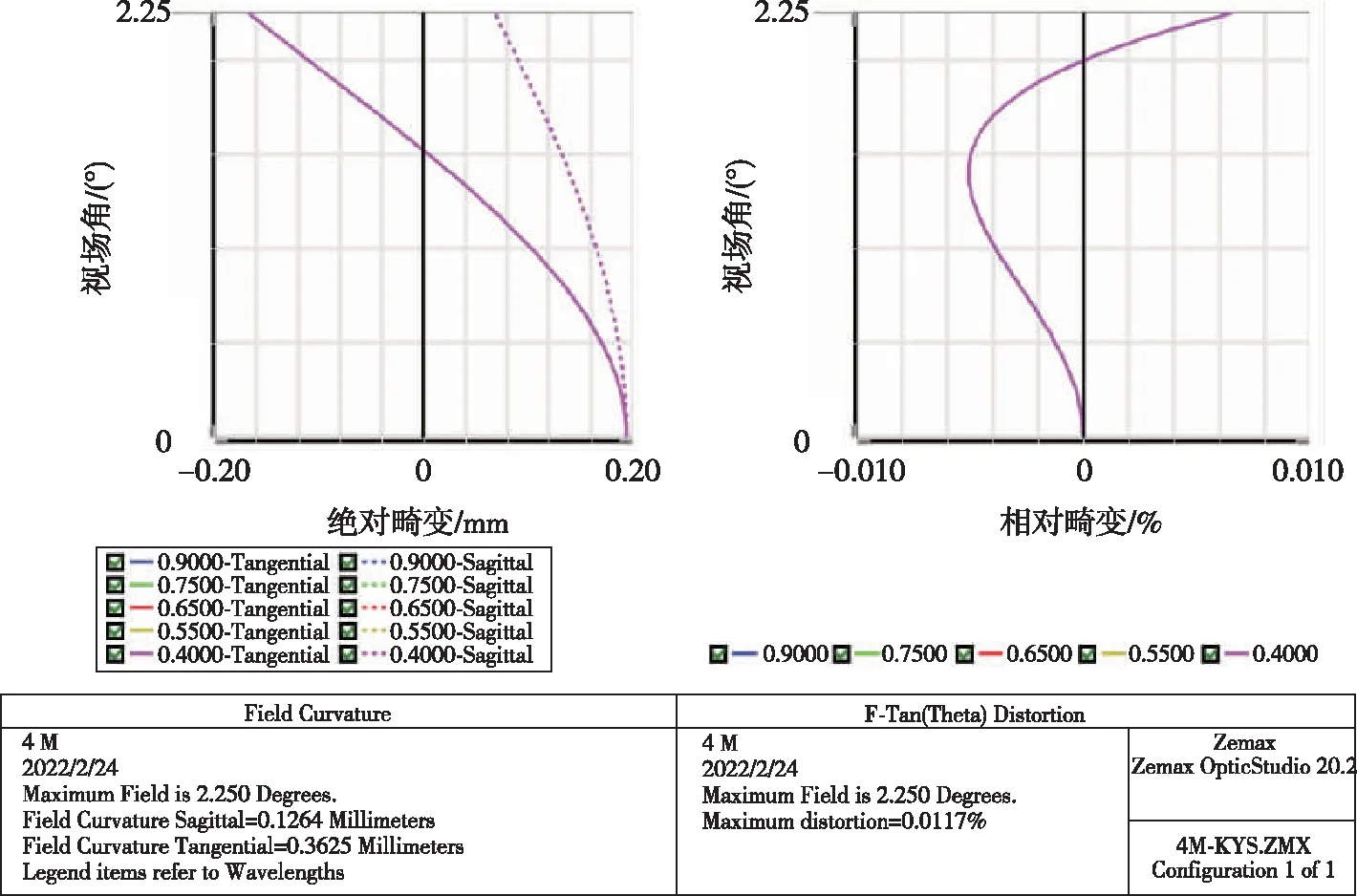
图5 星敏镜头场曲及畸变Fig.5 Field curvature and distortion of optical system

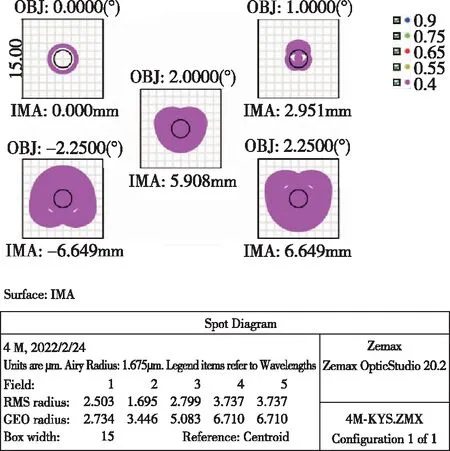
图6 全视场点列图Fig.6 Spot diagram for full field of view

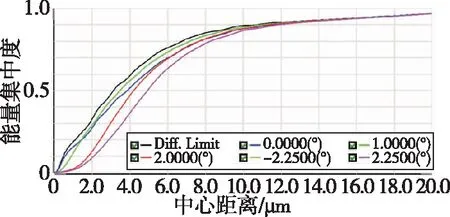
图7 能量集中度曲线Fig.7 Curves of concentration energy

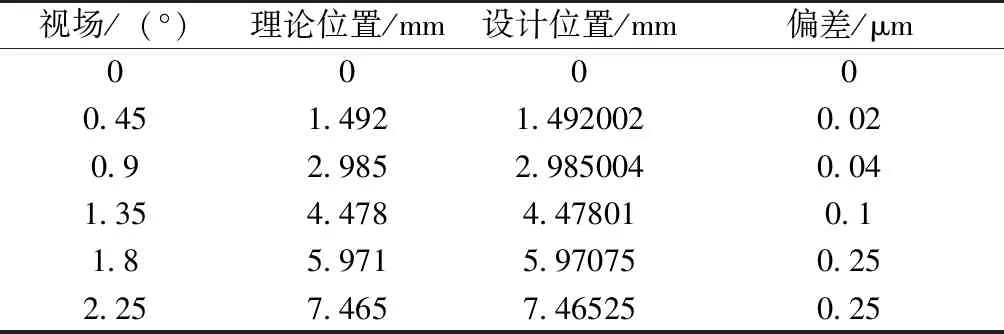
表2 弥散斑质心位置统计表

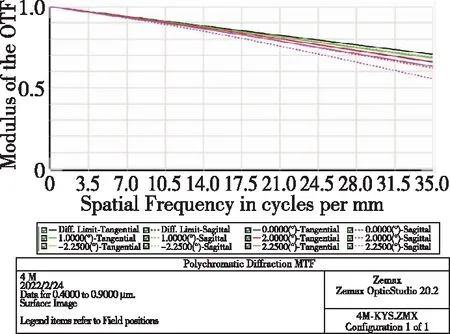
图8 系统全视场35lp/mm处传递函数曲线Fig.8 MTF at 35lp/mm for all field of view

3.2 公差分析

利用蒙特卡罗算法，以弥散斑作为评价标准，对镜头进行公差分析，得到公差分配表如表3所示。

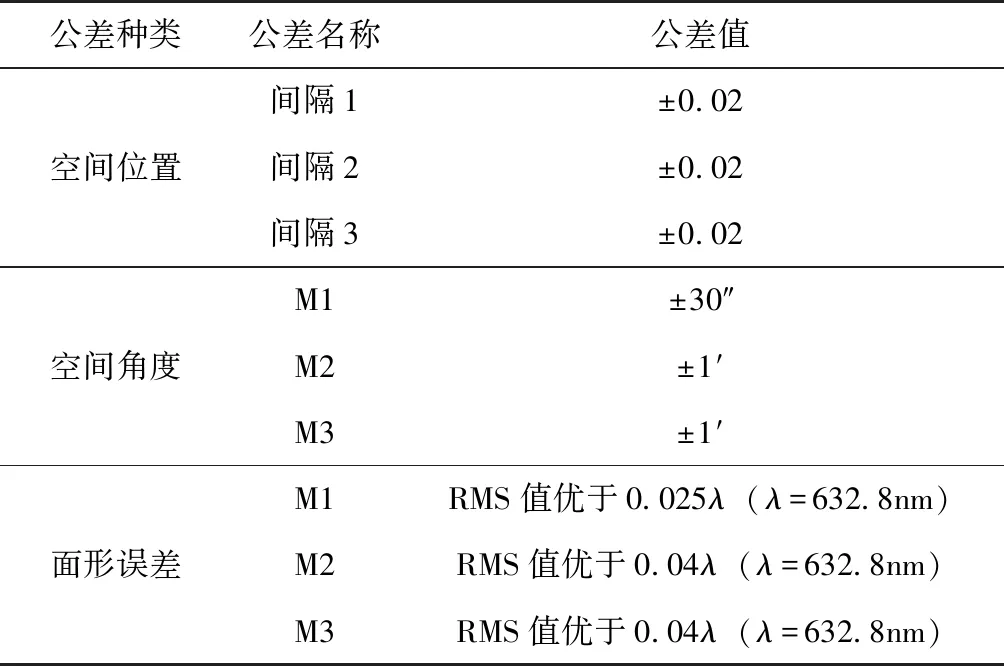
表3 星敏镜头公差分配表

为了适应恶劣的空间环境对相机焦面位置的影响，系统采用全钛合金结构，主镜、次镜和三镜采用单晶硅作为基底，利用金刚石单点车削的工艺完成加工，成本低廉，重复性好，满足工程需求。

4 遮光罩设计和杂散光分析

镜头前端设计有遮光罩，遮光罩长30mm，能够规避视场外2.5°～43°的杂散光，遮光罩分为内遮光罩和外遮光罩两部分，遮光罩示意图如图9所示。

系统具有良好的杂散光抑制性能，视场内系统的杂散光抑制性能在10-4量级，视场外各点源透射比如表4所示。

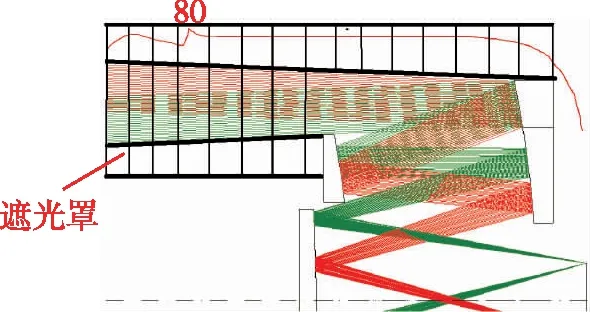
图9 遮光罩示意图Fig.9 Diagram of light shield

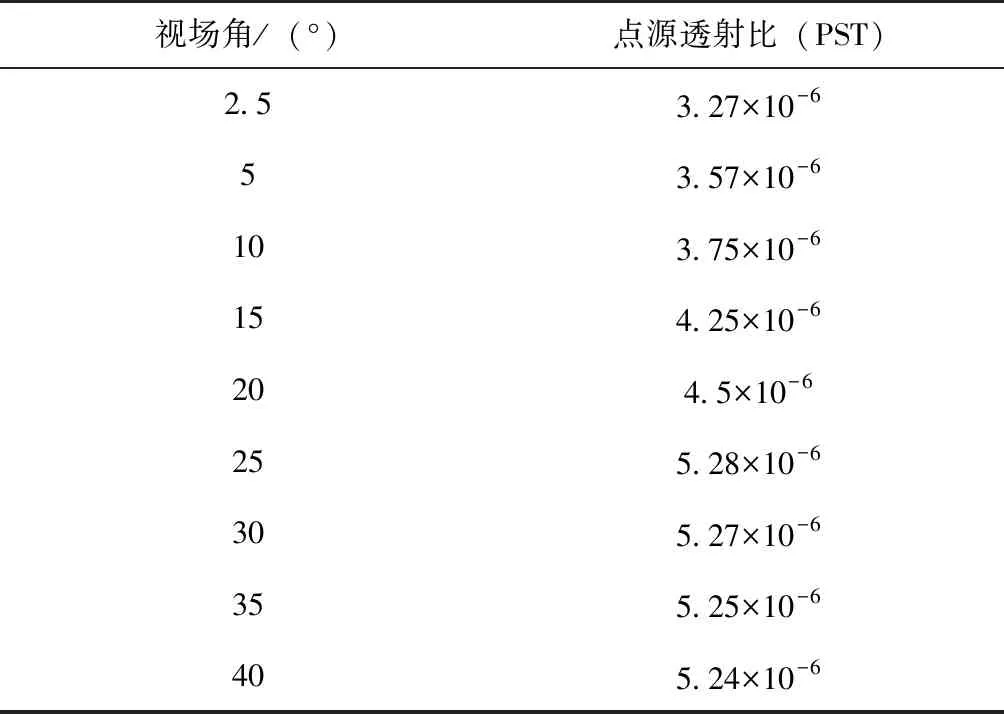
表4 点源透射比

5 结 论

在两反系统的基础上，引入了两块非球面反射镜，通过以弥散斑圆度为主的评价函数，进行本地优化和全局优化，得到了一种新的全反射星敏光学系统。该系统采用全反射形式，无色差，能够实现全谱段无差别成像，系统焦距170mm，筒长50mm，焦距筒长比1∶2.1，布局紧凑，公差分配合理，具有良好的杂散光抑制性能，满足星敏感器系统工程化批量化的需求。