基于正三角形模型的发射药燃气生成规律
张瑞华, 靳建伟, 张邹邹, 赵宏立, 王琼林
(西安近代化学研究所, 西安 710065)
目前,国内外对发射装药引起的膛炸机理已逐步形成共识,即“发射装药低温—挤压—破碎—增面—增燃—增压—膛炸”,发射装药膛内挤压破碎是药粒的低温脆性和弹底发射装药着火前受到挤压和摩擦作用的共同结果[1-2],而发射药在发生破碎后引起增面、增燃的燃气生成规律计算方法是模拟火炮膛炸亟待解决的难题,这是实现膛炸模拟的关键环节。
正常发射药的燃气生成规律是由几何燃烧定律推导出的形状函数来描述的[3-4],但是在膛内随机发生破碎后的发射药颗粒大小不同、形状各异,传统的形状函数计算方法已不再适用。大量学者通过试验或仿真对发生破碎后的发射药燃气生成规律进行了研究。Horst等[2]考虑发射装药的破碎对膛内压力异常的影响时,将弹底6%的发射装药燃面人为增加为未破裂前的2~5倍,仅在燃速系数上乘以系数,发射装药的形状不改变,应用此方法模拟了M110E2榴弹炮M188E1装药结构下炮尾膛炸的现象。Gazanas等[5-6]用落锤和高速液压伺服装置研究了M30、JA2发射装药的压缩和撞击力学性能,用小型密闭爆发器测量破碎药粒的燃烧规律,得到了破碎药粒的燃面是未破碎药粒的6倍的结论。翁春生等[7-8]在数值仿真过程中通过增加燃气生成速率达到增加燃面的效果。张小兵等[9]认为火药破碎后按比例破裂成大块、小块和粉末状3种类型,通过试验获得不同的颗粒间应力下3种碎药的质量分数。芮筱亭等[1]、Rui等[10]、Li等[11]、陈琪等[12]通过理论与试验获得了起始动态活度比定量表征发射装药破碎程度的方法,并建立了破碎发射药等效形状函数,用于计算破碎发射药的燃气生成规律,该方法需要通过试验获取参数。Jiang等[13]建立了基于离散单元法的发射装药挤压破碎程序,通过统计弹簧断裂个数来计算破碎发射装药初始燃面。以上研究是通过数据统计或者人为设定的方法预测发射药发生破碎后的燃气生成规律。
目前,离散单元法已经较为成熟的应用于发射装药由于挤压、摩擦作用导致的大规模破碎仿真研究[13-14]中,且获得实验验证,但是缺乏基于离散单元法发生破碎后发射药的燃烧规律计算方法研究。
现以广泛应用的花边19孔发射药为研究对象,建立考虑花边和内孔的发射药离散单元力学模型,构建正三角形燃烧模型和燃烧函数,并运用燃烧函数和传统形状函数对正常和破碎程度相同的发射药进行密闭爆发器燃烧规律数值仿真,验证燃烧函数模拟发射药发生破碎后增面、增燃的准确性。将该计算方法应用于基于离散单元法仿真获得的弹底破碎发射装药中,以期为模拟由发射装药破碎引起的火炮内弹道增压、膛炸现象提供技术支撑。
1 发射药离散单元力学模型
如图1所示,花边19孔发射药在纵向呈柱状,简化建立二维离散单元力学模型。依据真实发射药形状和尺寸,考虑花边和19个内孔,运用EDEM软件和颗粒替换方法[14-15],建立如图2所示的二维花边19孔发射药离散单元力学模型。离散小球颗粒半径r为0.067 mm,离散单元数为8 460,任意相邻的小球单元之间由黏结键连接,发射药的损伤、破坏通过黏结键的断裂来体现,且小球单元是发生破碎的最小单位。

图1 花边19孔发射药Fig.1 The lace 19-hole propellant
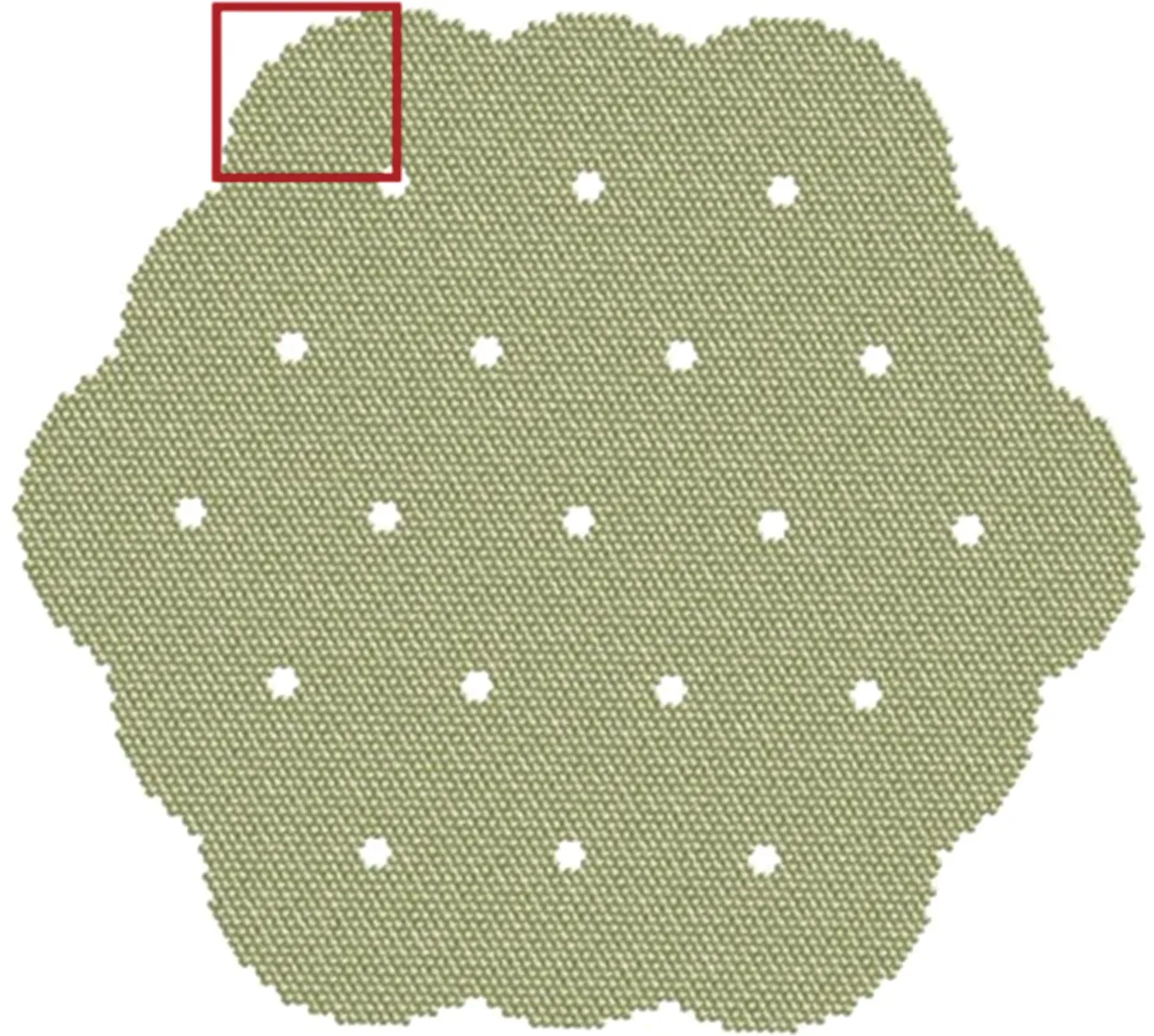
图2 花边19孔发射药离散单元力学模型Fig.2 Discrete element mechanical model of the lace 19-hole propellant
2 发射药燃气生成规律仿真理论
2.1 密闭爆发器燃烧经典理论
密闭爆发器定容情况下的火药气体状态方程如式(1)所示[1,3],火药已燃百分比ψ计算公式如式(2)所示,火药燃速公式如式(3)所示。通过仿真获得p-t曲线,即为发射药燃气生成规律。针对发生破碎的发射药,其难点在于计算已燃百分比ψ。
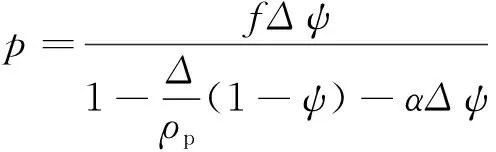
(1)
(2)

(3)
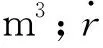
2.2 建立基于正三角形模型的燃烧函数
2.2.1 燃烧函数建模思路
建立发射药燃烧函数的基本思想如图3所示。为了清晰地表示建模过程,选取图2中红框内的局部力学模型进行详细说明,局部发射药燃烧模型建模过程如图4所示。具体步骤如下。
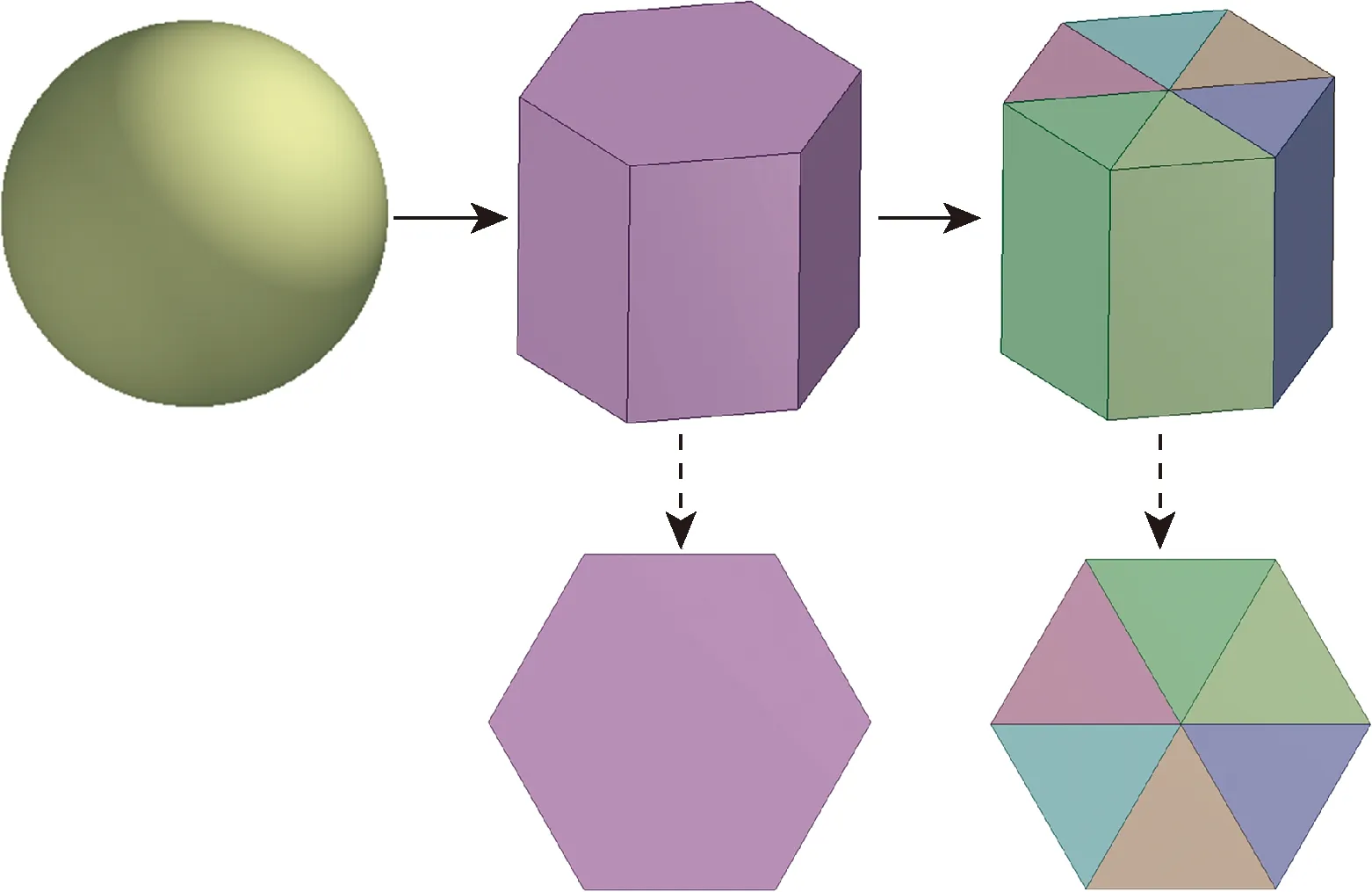
图3 燃烧函数建模思路图Fig.3 Thought diagram of combustion function modeling

图4 局部发射药燃烧模型建模过程Fig.4 Modeling process of combustion model of the local propellant
步骤1依据建立的发射药离散单元力学模型,预设小球颗粒离散单元代表一个正六棱柱块体,由于在纵向呈柱状,简化建立平面正六边形几何模型。
步骤2平面正六边形几何模型由6个正三角形组成,建立正三角形燃烧模型,推导燃烧函数。
步骤3所有正六棱柱块体都沿着与空气接触的燃烧面的平形层逐层燃烧,统计小球颗粒离散单元之间黏结键断裂情况,依据建立的燃烧函数计算出整个药床的燃烧剩余体积,再计算发射药已燃百分比ψ,从而计算获得密闭爆发器定容情况下的发射药气体压力。
2.2.2 建立燃烧函数
建立燃烧函数的基本假设如下。
(1) 所有的药粒具有均一的理化性质。
(2) 块体与空气接触的表面都同时着火。
(3) 所有药粒具有相同的燃烧环境,因此燃烧面各个方向上燃烧速度相同。
根据小球颗粒离散单元之间黏结键断裂情况,正三角形的燃烧函数分为7种,如表1所示。

表1 7种正三角形燃烧模型和燃烧函数Table 1 Seven equilateral triangle combustion models and combustion functions
根据建立的7种平面燃烧函数,某一种燃烧函数表达式为Si(e) (i=1,2,…,7);根据小球颗粒之间黏结键连接情况,正三角形燃烧模型燃烧层数为k,某一层燃烧模型对应的燃烧函数统计数量为Ni,j(i=1,2,…,7;j=1,2,…,k);正六棱柱块体纵向黏结键连接情况可分为3类:纵向无黏结键连接、纵向连接1个黏结键和纵向连接2个黏结键,对应统计数量分别为n0,i,j、n1,i,j、n2,i,j,满足Ni,j=n0,i,j+n1,i,j+n2,i,j;正六棱柱块体的初始高度均为l,则可计算整个药床的燃烧剩余体积Vall;计算公式如式(4)所示;从而计算发射药发生破碎的已燃百分比ψ,如式(5)所示,将其代入式(1)中用于发射药气体压力仿真研究。
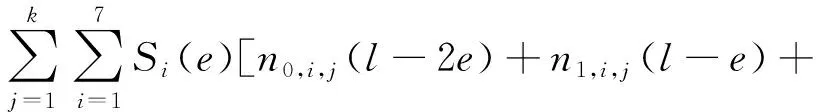
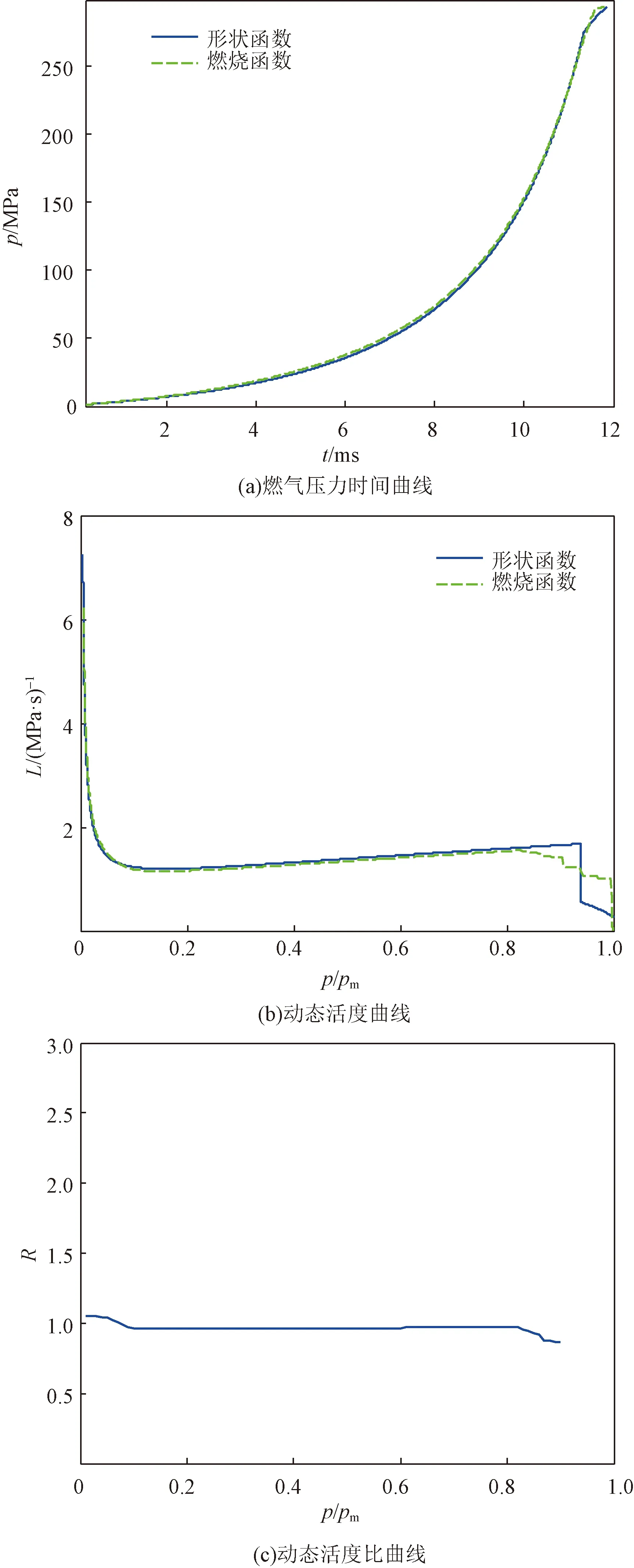
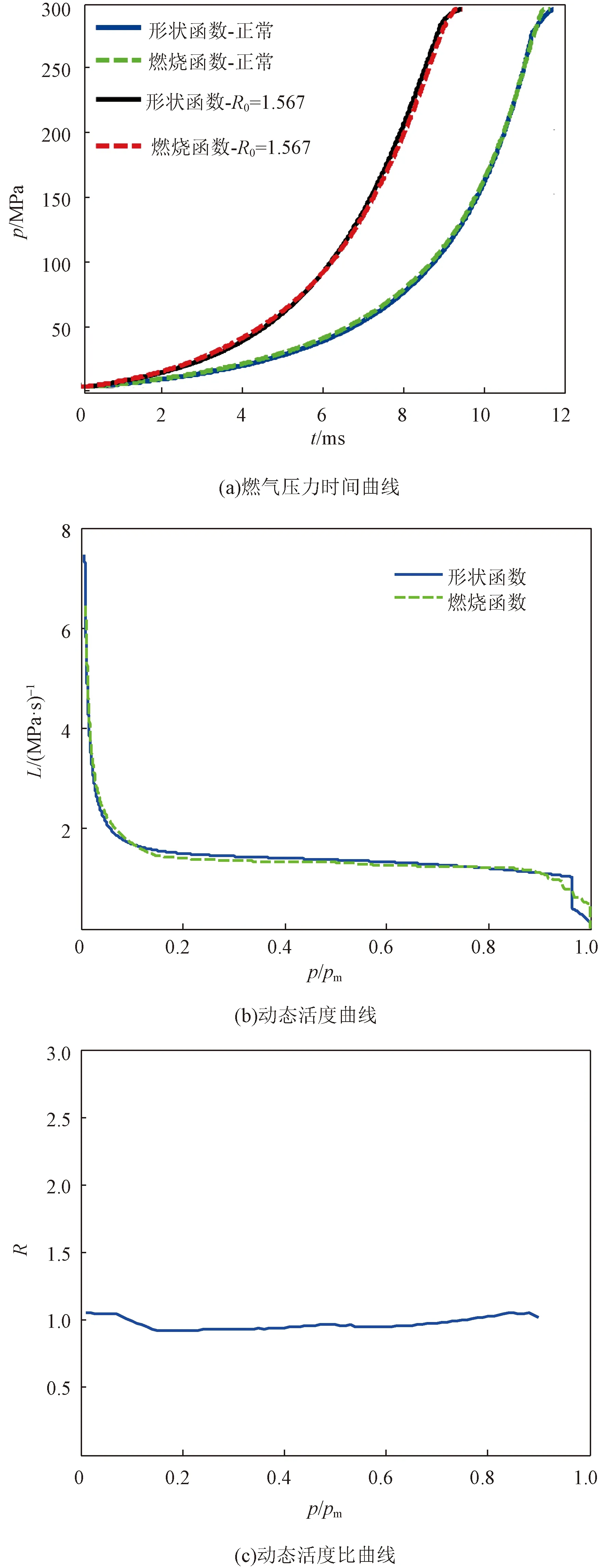
n2,i,jl], 0 (4) (5) 为了验证新建立燃烧函数的合理性和准确性,通过传统的形状函数[3]进行验证,形状函数如式(6)所示,将其代入式(1)、式(3)中用于发射药气体压力仿真,并与燃烧函数仿真结果进行对比分析。 (6) 式(6)中:χ、λ、μ、χs、λs为发射药形状特征量;Z为发射药相对燃烧厚度;Zk为燃烧结束时的相对燃烧厚度。 为了进一步验证新建立燃烧函数的实用性,引入发射药动态活度比R和起始动态活度比R0概念[1]。定义密闭爆发器中燃烧的发射药的动态活度L为 (7) 式(7)中:p(t)为气体压力,Pa;pm为发射药在密闭爆发器内产生的最大压力,Pa;dp(t)/dt为压力变化率,Pa/s。 动态活度比R为相等压力下破碎发射药与原未破碎发射药动态活度之比。已理论证明破碎发射药的动态活度比等于相同压力下破碎发射药与原未破碎发射药的面积比S/S0[1],发射药起始动态活度比R0为发射药被点燃时刻的发射药动态活度比。计算公式为 (8) 式(8)中:L′为破碎发射药动态活度,(Pa·s)-1;L0为原未破碎发射药动态活度,(Pa·s)-1。研究中选取L′为形状函数计算获得的发射药动态活度,L0为燃烧函数计算获得的发射药动态活度。 由式(7)可以看出,由密闭爆发器仿真获得压力时间曲线后,即可求得其动态活度和起始动态活度比,用来验证新建立的燃烧函数计算发生破碎发射药增加燃烧面积的准确性。 由于建立的燃烧函数是二维的,为了检验平面燃烧函数统计判断是否正确、验证燃烧规律计算是否有效,通过预设发射药破碎形式进行研究,而在实际研究过程中为挤压仿真获得的随机破碎发射药。预设如图5所示发生破碎的发射药模型,呈中心十字形裂成4块,建立了如图5(a)所示的单层发射药离散单元力学模型;建立的局部[图5(a)红框内力学模型]正六边形几何模型和正三角形燃烧模型分别如图5(b)、图5(c)所示;正常和发生破碎的发射药在纵向高度l均为17 mm,纵向黏结键连接情况只存在一种情况:纵向无黏结键连接,即n0,i,j=Ni,j、n1,i,j=0、n2,i,j=0。 图5 发生破碎的发射药燃烧模型建立过程Fig.5 Establishment process of combustion model of propellant after fracture 建立的正常和发生破碎的发射药离散单元力学模型中离散单元数量均为8 460,则正三角形燃烧模型数量为8 460×6=50 760。表2、表3所示为对正常和发生破碎的发射药的燃烧函数统计结果,发射药的燃烧层数k为16层,由第1层到第16层逐层燃烧,Ni(i=1,2,…,7)表示某层燃烧的正三角形燃烧模型数量对应的燃烧函数统计结果,第1层中未燃烧和已燃烧的共计数量为50 760,为初始正三角形燃烧模型数量;从第2层起共计数量均为上一层未燃烧数量,表明燃烧函数统计结果正确;对比表2和表3,在相同燃烧层数下,表3中的未燃烧数量统计结果均小于表2,表明燃烧层数相同时,发生破碎的发射药已燃百分比大于未破碎发射药。 表2 正常发射药燃烧函数统计结果Table 2 Statistical results of the combustion function of normal propellant 表3 发生破碎的发射药燃烧函数统计结果Table 3 Statistical results of the combustion function of propellant after fracture 图6所示为图5(c)中局部正三角形燃烧模型的燃烧层数判断模型(前5层),每层颜色代表某层正三角形燃烧模型,画图时5种颜色(黑色、蓝色、红色、绿色、黄色)依次循环,空白部分表示发射药未燃烧部分,可以看出发射药沿着与空气接触的面逐层向内燃烧,通过图6(e)中内孔细节可以看出燃烧模型判断正确。正常和发生破碎的发射药燃烧层数判断模型如图7所示,可以看出燃烧层数为16层,分别对应表2、表3中的燃烧函数统计结果,充分说明燃烧模型统计结果判断正确。将表2、表3的统计结果代入式(4)即可计算发射药的燃烧剩余体积Vall,然后通过式(5)、式(1)、式(3)计算密闭爆发器燃气压力。通过燃烧函数和形状函数分别进行正常和发生破碎的发射药密闭爆发器仿真研究。 图6 发生破碎的发射药燃烧层数示意图(前5层)Fig.6 Schematic diagram of the number of combustion layers of propellant after fracture (the first five layers) 图7 发射药燃烧层数示意图Fig.7 Schematic diagram of the number of combustion layers of propellant 运用燃烧函数和形状函数进行密闭爆发器燃气压力仿真初始参数均相同,仿真装填密度均为0.2 g/mL。对于正常发射药,密闭爆发器压力时间对比曲线如图8(a)所示,曲线吻合较好;依据式(7)处理得到图8(b)所示动态活度曲线,进一步依据式(8)处理得到燃烧函数与形状函数在仿真过程的动态活度比曲线,如图8(c)所示,可以看出燃烧表面积之比在1.0左右,表明燃烧函数可以描述正常发射药的燃烧面积和燃气生成规律。 图8 正常发射药燃烧规律仿真结果Fig.8 Simulation results of combustion laws of normal propellant 当运用燃烧函数,图5(a)中发生破碎的发射药燃烧初始表面积是正常发射药的1.567倍,即起始动态活度比为1.567;当运用形状函数,令发射药的破碎方式为取0.219倍原发射药高度,起始动态活度比为1.567,达到两种仿真方法用的破碎发射药初始表面积相同的目的。分别运用燃烧函数和形状函数计算发生破碎发射药的燃气生成规律,仿真结果如图9所示,发现在相同起始动态活度比下压力时间曲线吻合较好,且燃烧函数与形状函数在仿真过程的燃烧表面积之比值也在1.0左右,同样表明燃烧函数可以描述基于离散单元法仿真发射药发生破碎引起的燃气生成规律变化。以上结果验证了建立的燃烧函数的有效性和合理性,且具有较高可实施性。 图9 发生破碎的发射药燃烧规律仿真结果Fig.9 Simulation results of combustion laws of propellant after fracture (1) 首次通过预设离散单元模型代表正六棱柱几何模型,进一步简化为正三角形燃烧模型,推导和建立了7种燃烧函数,具有建模方法简单易懂、燃烧函数类型少、适用性强等优点。 (2) 运用传统的形状函数和新建立的燃烧函数对正常和破碎程度相同的发射药进行密闭爆发器仿真,结果表明新建立的燃烧函数不仅能模拟正常发射药的燃气生成规律,同时能够精确计算基于离散单元法仿真获得的发射药破碎引起的燃烧规律变化。 (3) 研究结果为科研人员提供了一种基于离散单元法的发射药发生随机破碎的燃气生成规律计算新方法和新思路;为进一步进行伴随发射装药挤压破碎的内弹道两相流仿真从而预测膛炸现象的研究提供了技术支撑。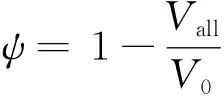
2.3 形状函数
2.4 起始动态活度比理论

3 发生破碎的发射药燃气生成规律仿真及验证
3.1 发生破碎的发射药离散单元力学模型

3.2 燃烧函数统计结果
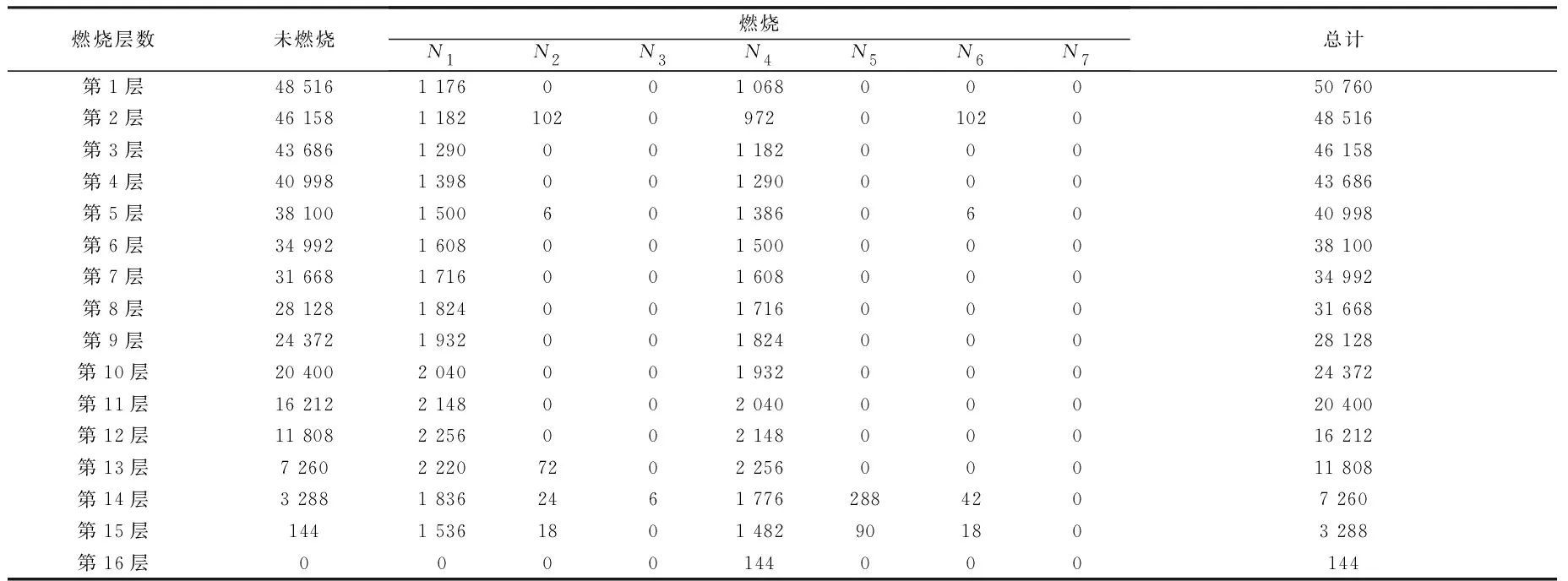

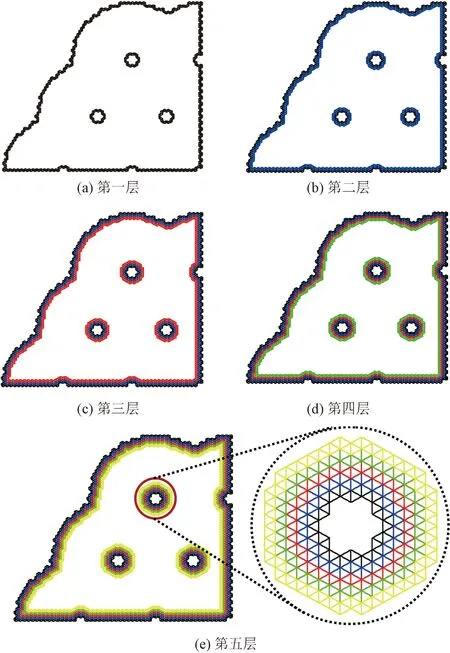
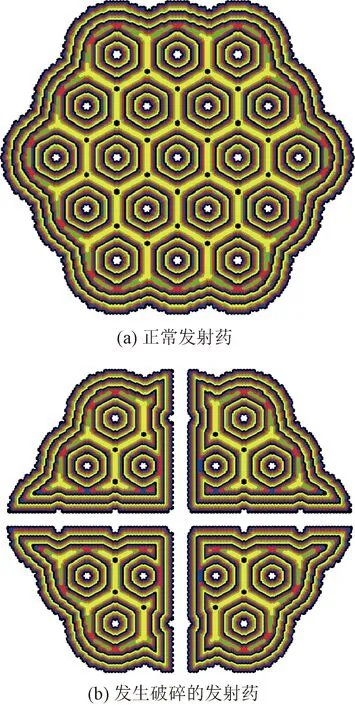
3.3 燃烧函数验证
4 结 论

