巧用概念的图式表达，建构高效数学课堂

【摘要】数学作为小学教育阶段的一门基础性学科，对小学生的空间想象能力与逻辑思维能力有着较高的要求。掌握数学知识体系中大量的概念，是学习数学知识的基础，也是数学学习中的一大难点。对此，教师可巧用概念的图式表达，建构高效数学课堂。

【关键词】概念；图式表达；高效；数学教学

作者简介：凌辉（1978—），男，江苏省南通市海门区正余小学。

数学概念是从客观现实中抽象出来的，具有高度的抽象性与概括性特征，是学生需要学习、感知与理解的关键内容，更是有助于他们学习其他数学知识、解题及实际应用的重要内容［1］。图式表达是将数学知识以图的形式来展现，小学数学教师在概念教学中可采用图式表达引领学生观察与分析，帮助他们高效地构建数学概念，为后续学习夯实根基。

一、借助图式表达优势，转变概念呈现形式

（一）运用图式表达，使抽象概念变得形象化

小学生正处于形象思维占据主导地位的阶段，而数学知识具有显著的抽象性特征，概念则更加抽象［2］。在概念教学中，小学数学教师需极力发挥出学生的形象思维优势，巧用图式表达，将具体的概念以图片、图表或图文并茂的形式来呈现，以此使抽象的数学概念变得形象化，这样不仅与学生的认知特点相契合，还能够激发他们参与学习的兴趣。

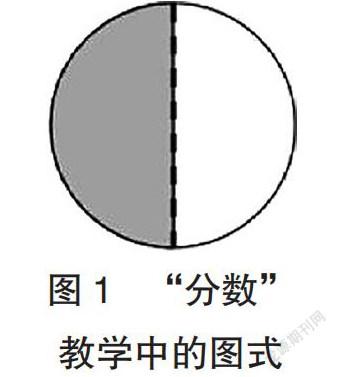
例如，在进行“分数的初步认识（一）”的教学时，教材中对“分数”概念的解释为：分数表示一个数是另一个数的几分之几，或一个事件与所有事件的比例。把单位“1”平均分成若干份，表示这样的一份或几份的数叫分数。对于三年级学生来说，文字性介绍是比较难以理解的，因为这样的描述、用语十分严谨，而他们的抽象思维能力恰恰不强。针对这一情况，教师在课堂上运用图式表达转变了“分数”这一概念的呈现形式，在多媒体课件中展示画有一个圆的图式（如图1所示）。图中的一条虚线将圆分成两半，一半是灰色，一半是白色。然后，教师询问：“这个圆被虚线分成的两份是不是一样大？每份是不是均为这个圆的一半？可以用什么数来表示？”学生经过观察、思考与讨论后回答了上述问题。教师结合他们的答案指出：“这个圆被平均分成了2份，每份是这个圆的一半，一半即为1/2。”教师通过图式表达形象地引入“分数”的概念后，要求学生结合图片说出1/2中的“2”和“1”分别表示什么意思，并在课件中展示其他图形让学生进行练习，继续辨认1/2。

（二）应用图式表达，使复杂概念变得简单化

在小学数学概念教学中，图式表达可以让学生一目了然，便于他们更好地学习、内化与掌握数学概念，为之后的运用做好准备。在小学数学课程教学中，当讲授到概念类的知识时，教师可以应用图式表达的方法，将学生仅通过阅读文字难以明白的内涵，利用图的形式来展示，使学习内容显得清晰、明了，使复杂的数学概念变得简单化，借此辅助他们深入理解概念的内在意义。

以“小数的初步认识”的教学为例，教师从小数的意义切入来描述“小数”的概念：“将整数1平均分成十份、一百份等得到的十分之几、百分之几等，能用小数表示。一位小数表示的是‘十分之几’，两位小数表示的是‘百分之几’，等等。在小数中，相邻两个计数单位之间的进率为10。”教师发现，虽然自己费尽心思运用语言来描述，但不少学生仍然未能真正理解，原因是“小数”的概念从文字视角来看较为复杂，而且这对于学生来说是一个新概念，他们极易把“分数”“整数”等概念混淆。于是，教师应用图式表达，以实物的形式辅助学生重新构建“小数”概念，先拿出一把标有清晰刻度的直尺和一支长约4厘米的铅笔，再将铅笔的一端同直尺的0刻度線对齐，让学生观察后说出铅笔的长度。学生发现铅笔的另一端在直尺的4至5刻度之间，这说明铅笔的长度并非整数，于是纷纷产生“该如何表达铅笔的长度？”的疑问。这时教师点拨：“大家在进行计算或测量时，假如遇到结果非整数的情况，就要使用小数来表示。”这样不仅可以使复杂概念变得简单化，还巧妙地穿插了小数的用法。

（三）利用图式表达，使零散概念变得系统化

不少学生在学习数学概念时习惯采用死记硬背这种机械的方式，也就是说，他们把平常可能用到的一些概念背诵得十分熟练，以此应付作业与考试。但采用这样的方式有一定的弊端，即学生往往只掌握了零散的概念，而未学会系统化地运用这些概念。面对这一不利局面，小学数学教师在概念教学中，可利用图式表达将零散的数学概念整合在一起，使其变得系统化，方便学生在后续解题中综合运用，提高做题效率。

举个例子，对于“平行四边形的面积”这部分内容，教材结合转化思想归纳出平行四边形的面积公式。但由于部分小学生的逻辑思维能力和推理能力不强，很难透彻理解这一公式的推导过程及有关概念，因此教师对原有教学内容进行加工，借助图式表达的方式改进了教学过程。在课堂上，教师未直接给出平行四边形面积的公式，而列出了式子S=ah，并指出a与h分别表示平行四边形的底与高，同时展示对应的图式（如图2所示）。因为学生已经学习过长方形的面积公式，所以教师就让他们试着将未知的平行四边形转化成已知的长方形。根据这一图式表达，学生在教师的引导下拿出准备好的平行四边形纸片，沿着高将平行四边形剪开，将剪下来的梯形平移至平行四边形的另外一边，拼接在一起，使它们构成一个长方形，进而发现新的长方形的长、宽就是平行四边形的底、高。教师通过图式表达的演示，让学生了解到长方形的面积与平行四边形的面积相同。如此，教师利用图式表达，引领学生把平行四边形的面积公式、概念与长方形的知识相关联，能够使他们形成系统化的认知网络，加深他们对转化思想的认识，为他们接下来的学习提供更多助力。

二、以图式表达创设情境，降低概念理解难度

（一）结合生活进行图式表达，辅助学生学习概念

在小学数学概念教学中，教学的基础是引入概念，引入概念以后，教师就需要引领学生感知概念，让他们真正理解概念的内涵，方便他们之后的运用。在实际生活中，数学现象与问题可谓随处可见，小学生平常也积累了一定的生活经验，因此数学教师在概念教学中应该紧密结合生活素材，将一些生活化资源融入课堂，运用到概念讲解环节中，并将其当作学生感知与理解概念的工具，由此降低概念的学习难度，辅助他们更好地掌握数学概念。

比如，在开展“倍”的概念教学时，教师先要求学生认真观察教材中关于“两、三位数乘一位数”这部分内容例3的情境图，自己动手数一数各种不同颜色的花朵数量，并引出问题：“如何清楚地看出不同颜色的花朵之间的关系？”学生想到逐个对应摆放与排列等方式。教师让学生结合找到的信息自主提出问题。如学生提问蓝花和黄花一共有多少朵，红花比黄花多多少朵，红花的朵数是蓝花的多少倍。教师顺势引出新知识，唤起学生的生活经验，让他们初步感知倍是两个数之间的比较关系。接着，教师鼓励学生将刚才获得的信息与说出的问题进行归纳。当有的学生提到将2朵蓝花看成1份时，教师让其简要说出原因所在，然后讲述：“黄花有这样的3份，也就是有3个2朵。你们数一数是不是这样？”教师在学生数完后借机指出黄花的朵数是蓝花的3倍。最后，教师提出“红花的数量与蓝花的数量相比又是什么关系？”的问题，引导学生进行知识迁移，从而发现红花的数量是蓝花的4倍；并使其思考为什么黄花、红花都是同蓝花的数量相比，倍数却不同，旨在让他们在图式表达的辅助下建立“倍”的表象，通过对比深入感知“倍”的概念。

（二）运用信息技术手段，以图式表达模拟情境

小学生年龄比较小，逻辑思维能力还未得到很好的发展，对数学概念的感知以形象思维为主，再加上部分学生在学习过程中容易受到外界环境的影响和干扰，以致注意力很难长时间集中，最終影响他们内化数学概念。这就要求小学数学教师在平常教学中紧跟时代步伐，灵活运用信息技术手段进行图式表达，通过图片、视频、动画等形式模拟情境，使概念的学习内容变得有趣、生动，吸引学生的注意力，让他们认真观察与深入思考，促使他们轻松理解数学概念。

例如，在“垂线”的概念教学实践中，教师先要求学生观察教材中关于“垂线与平行线”这部分内容例6中的三幅图片，并利用信息技术手段分别从每一幅图中截取两条相交的直线，在多媒体设备的大屏幕上显示出来，让他们基于相交情况对这三组线进行分类。接着，教师指导学生用三角尺的直角分别与三组线形成的角进行比较，使其感知到第一组线相交形成的角不是直角，后两组线相交形成的角都是直角，并认识到垂直是相交的一种特殊位置关系。然后，教师将第二幅图放大，闪动其中一个角，提问：“假如这个角是直角，那么你们能知道其他三个角的角度吗？”学生经过思考、探讨后判断出其他三个角均为直角。教师让学生讨论交流“结合上述图式，你们认为两条直线在什么情况下才能被称作‘互相垂直’？”这个问题。在学生发言后，教师强调两条直线要相交成直角才能被称作“互相垂直”，让他们用手势表示“垂直”。最后，教师在多媒体课件中展示几组相交的线段，让学生判断它们是否互相垂直，并说明理由，加深他们对“垂线”等概念的理解。

三、巧妙引入图式表达，优化概念教学形式

（一）应用图式表达进行整理，深化对概念的理解

抽象性是数学知识的显著特点之一，部分小学生自身学习能力一般、理解能力不强或认知水平有限，很难快速发现知识中所蕴含的数学概念，这就要求教师在日常教学中应用图式表达对数学概念进行整理，优化概念教学形式，使隐蔽的关系变得明了，同时积极引导学生观察、想象与猜测，进而发掘出知识中所隐含的概念性内容，这样不仅可以满足他们的求知欲望，还可以拓展他们的思维空间，深化他们对概念的理解。

例如，在实施“梯形”的概念教学时，教师并未急于讲授新课，而引入了旧知识，引导学生回顾学习过的“四边形”这一数学概念，再提出“梯形、长方形、正方形、平行四边形的对边分别有什么特点？它们之间存在着什么样的联系？”的问题，让他们在小组内自由讨论和交流，要求他们将这几种平面图形整合在一起，画出图式，从而让他们整理小学阶段所学的各种四边形概念，形成完整的数学概念网络，了解这些不同的四边形之间的关系。有的学生在问题驱动下积极思考和互动，画出如图3所示的图式。如此，学生在图式表达的辅助下不仅可以更好地理解“梯形”的概念，还可以回顾其他四边形的概念，掌握它们的区别与联系，培养自身的逻辑思维能力，优化自身的知识结构。

（二）运用图式表达进行归纳，改善对概念的认知

部分小学生在学习数学概念的过程中会出现这样一种错误，即混淆了相关或者相近的概念，以致在做题时遇到障碍，甚至出现张冠李戴的情况，无法顺利解决问题。究其原因主要在于大部分数学概念是比较抽象难懂的，这些学生对概念的理解还停留在表面，没有真正掌握概念的内涵。对此，小学数学教师可运用图式表达，对相关概念进行归纳，让学生对概念的感知由模糊变为清晰，改善他们对概念的认知，便于他们后续应用。

比如，“分数的意义和性质”一课中出现多个新的概念，包括单位“1”、分数和分数单位等，其中单位“1”是建构分数概念的出发点。教师在讲授的过程中可采用图式表达辅助教学，要求学生观察教材的这部分内容例1中的四幅图片，用分数表示每幅图中涂色的部分，写好以后想一想各个分数分别表示什么，鼓励他们大胆说出各自的想法与见解，同时板书“1/4，5/8，3/5，”1/3，带领他们回顾“平均分”的概念。然后，教师以第四幅图中的1/3为例，提问：“这里将6个圆看作一个整体，将它们平均分成3份，涂色部分是其中的1份，也就是1/3。那么前三幅图中的分数是把什么平均分后得到的呢？第四幅图和前三幅图相比有什么不同？”教师顺势引出“单位‘1’”的概念，组织学生在小组内交流，讨论这与之前所学的“1”有什么不同，旨在让他们意识到之前所学的“1”只能表示“1个”，而现在学的“单位‘1’”可以表示许多含义，如表示“1块饼”“1个长方形”“1条1米长的线段”“由6个圆组成的1个整体”等，进而改善自身对数学概念的认知。

结语

综上所述，在小学数学教学实践中，教师要将概念教学放在重要地位，巧妙运用概念的图式表达创新教学方法与形式，以文字解释为前提，结合几何图形、图表等图式为数学概念的学习搭建起具象化的支架，促进学生对概念的理解与内化，并根据不同概念运用不同的图式表达方法，全力建构高效数学课堂，使学生对数学概念形成结构化、系统化的认知。

【参考文献】

［1］ 董兴华.让数学学习不再“雾里看花”：例谈小学数学概念教学的策略［J］.新课程，2021（35）：86.

［2］张晶.互联网思维下的小学数学概念教学：以“分数”的教学为例［J］.江苏教育，2021（61）：42-45.