面向需求响应日前市场投标的负荷聚合商决策动力学分析

柏 颖，刘晓峰，陈雪颖

（1.南京师范大学电气与自动化工程学院,江苏省南京市 210023；2.江苏省综合能源设备及集成国际联合实验室,江苏省南京市 210023）

0 引言

构建以新能源为主体的新型电力系统需要优化电网调度运行和商业模式,重新定位各能源主体功能,对供给侧和需求侧进行转型,形成新的运营体系［1-3］。电力体制改革以来,电网与负荷的双向互动可行性越来越高,为应对系统运行日益增加的负荷需求以及高比例新能源并网造成的不确定性,从需求侧充分挖掘柔性负荷资源参与源荷互动将成为必经之路。基于需求响应（demand response,DR）手段,高效管理需求侧负荷,可以达到削峰填谷的效果,实现资源有效配置,进而促进电力行业低碳可持续发展［4］。

在需求侧负荷资源中,居民用户基数大、用电弹性高,DR 参与潜力大［5-6］。然而,由于单个用户负荷弹性水平低,无法直接参与DR 市场,造成了柔性负荷资源的大量浪费。鉴于此,业内提出通过负荷聚合商（load aggregator,LA）整合居民用户柔性负荷资源,使其达到参与DR 市场的准入门槛,充分发挥居 民DR 的 市 场 效 用［7-8］。LA 作 为 中 间 机 构 引 入DR 市场,既充分整合了居民柔性负荷资源,降低了资源的浪费,又能以市场主体身份参与DR 市场投标,极大地提升了DR 市场运行效率［9-10］。

目前,国内外关于LA 的研究主要侧重于优化调度以及市场投标模型的构建。文献［11］提出了空调负荷的双层优化调度模型,LA 通过不断完善对空调负荷的控制策略,使其实际出力与调度计划尽可能一致,保证其利益最大化。文献［12］构建了以LA 利润最大化为目标的日前投标博弈模型,并给出了纳什均衡解的存在性证明。文献［13］以柔性LA 投标支出最小化为目标,利用可调鲁棒控制系数处理电动汽车充电行为的随机性,得出不同时段LA 购售能量的投标策略。文献［14］研究了基于价格激励的DR 机制,建立考虑用户偏好的LA 收益模型,求解获得其最优定价策略。文献［15］计及风险因素和需求侧资源不确定性,构建了基于双重市场的LA 投标量分配和利润模型,在日前电能市场的约束下,其投标决策偏保守。

上述研究主要以居民用户柔性负荷资源为约束,建立LA 利益最大化的投标或定价模型,最后进行优化求解,但对LA 参与市场决策行为的动态特性研究涉及较少。然而,在实际DR 市场中,受市场信息、决策者认知能力等因素的影响,参与日前投标的LA 其有限理性程度存在差异性,且无法做到完全理性决策,尤其是在DR 项目实施的初始阶段。随着DR 项目的深入推进,LA 势必会在市场竞争中不断积累经验,提升理性决策能力,从而不断调整自身投标策略,以期能够达到完全理性状态下的最优策略,但制定每期投标策略时无法从有限理性突然跃升为完全理性,必然会参考之前的决策和收益情况,而LA 该决策行为的动态变化又会影响整个投标市场。因此,从长时间尺度来看,LA 参与DR 日前市场投标实际上是一个长期重复博弈的动态决策过程,通过对该过程的研究分析,可以更准确地刻画出DR 市场动态特性以及发展趋势,进而为DR 市场机制的完善提供决策依据［16-17］。鉴于此,为更贴近真实的市场竞争机制,本文基于常见的几种有限理性决策模型构建了LA 日前市场投标非合作博弈动态模型,进而对该动态系统的平衡点进行稳定性分析,并引入延迟反馈控制法对市场失稳进行稳定控制,最后通过算例仿真对LA 市场投标竞争进行动力学特性分析。

1 LA 参与DR 市场投标机制

本文所述场景中,在DR 日前市场,电力公司调度部门根据历史负荷数据预测下一周期负荷水平,并将削峰时段和价格信息公布给LA,LA 为了实现利益最大化,会在市场中进行负荷削减量的投标,并与其他LA 一同竞争市场份额。在参与市场投标前,LA 和居民用户签订合约,获取用户负荷控制权,并根据用户用电特性确定管辖区域柔性负荷聚合量上限,进而将其作为DR 日前市场投标约束,与其他LA 参与市场份额的竞争。本文所述场景下,重点关注LA 参与DR 日前市场投标决策的动力学特性,至于用户柔性负荷的具体调度策略并非本文重点,此处不再探讨。

根据美国PJM 市场相关规则,本文假设LA 参与DR 市场投标价格与负荷水平之间存在线性关系［18］,具体市场价格和负荷水平关系如式（1）所示。

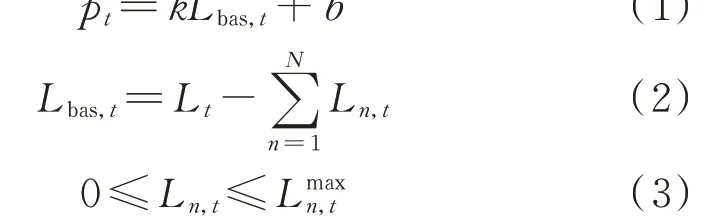
式中:pt为DR 在周期t内的市场投标价格；Lt为电力公司调度部门在日前预测的周期t内的用户负荷水平；Ln,t为LAn在周期t内的市场投标量；N表示假设市场中存在N个LA 参与市场投标；Lbas,t为在周期t内按照LA 投标量进行削减之后的用户负荷水平；Lmaxn,t为周期t内LAn管辖区域内可提供的最大负荷削减量；k>0 为价格参数；b为常数项。

由式（1）可知,用户负荷水平和LA 市场投标量均会影响市场价格,负荷水平越高、市场投标量越低,则市场价格越高,反之则市场价格越低。因此,LA 市场收益不仅取决于自身投标量Ln,t,还与其他竞争对手的投标决策相关,因而LA 在参与市场投标时必定存在非合作博弈竞争［19］。鉴于此,本文将基于非合作博弈理论对LA 参与市场投标的纳什均衡以及长时间尺度下投标均衡解的动力学特性展开分析,从而为DR 市场高效运营提供决策依据。

2 LA 市场投标决策模型

2.1 LA 市场投标决策调整机制

LA 参与DR 市场投标时,可从市场中获取一定的收益,但同时也需要向用户支付相应的补偿费用。因此,LAn在周期t内的利润πn,t可表示为:

在DR 市场中,LA 受市场复杂度、决策者理性程度等因素影响,短时间内无法达到最优决策状态,必须通过掌握市场信息并提升自身决策能力,才能不断优化投标决策。由于各LA 有限理性程度存在差异性,基于常见有限理性决策调整机制,假设DR市场中参与投标的LA 主要存在以下几类决策方式。

1）第1 类:LA 理性程度较低,主要基于本期市场投标边际利润,对下一期投标量决策进行调整。若本期边际利润为正,则下一期将增加投标量,反之则减少投标量,即

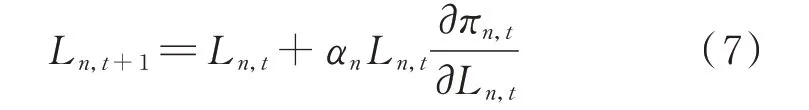
式 中:αn≥0 为LAn投 标 量 调 整 速 度,其 值 可 体 现LA 对边际利润的反应能力。

2）第2 类:LA 理性决策水平较第1 类有所提高,除了参考本期边际利润外,还会综合上一期边际利润,以使决策更加合理。根据t和t―1 周期的边际利润来制定t+1 周期的投标策略,即

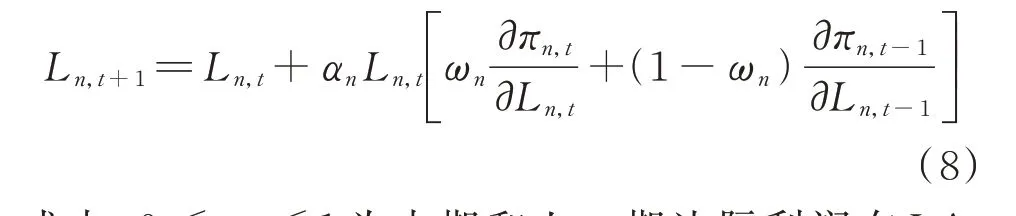
式中:0 ≤ωn≤1 为本期和上一期边际利润在LAn决策调整中所占的权重。

3）第3 类:LA 具有一定的自适应调整能力,会基于本期决策和本期最优投标量决策进行线性调整,以此制定下一期投标策略,即

通常,参与DR 日前市场的LA 数量众多。为便于建模分析,假设投标市场存在以上4 类LA,且同一类型LA 作为整体参与市场投标决策,其参与市场投标的非合作博弈动态模型可表示为:

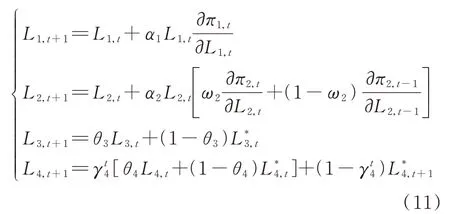
2.2 博弈动态系统平衡点求解

针对LA 市场投标博弈动态系统（式（11））的均衡点求解问题,考虑到当系统处于稳定状态时,市场各LA 在t周期和t+1 周期决策量会趋于稳定。由此,可得如下非线性动力学系统:

以上4 个解集分别代表4 类LA 参与市场竞争后的投标决策结果,要求ε1、ε2、ε3、ε4各均衡点中的分式分子皆大于0,此时各点集才具有经济意义。

2.3 DR 市场决策的均衡点稳定性分析

本节内容主要针对上述均衡点的稳定性进行分析。由动态系统式（11）可得如下Jacobi 矩阵:

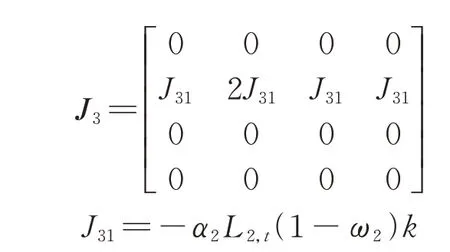
将各均衡点解集代入Jacobi 矩阵,并求其特征值,根据特征值的大小判断各均衡点的稳定性。以有界均衡点ε1为例,其Jacobi 矩阵J(ε1)为:

式中:λ为特征方程的参数。根据均衡点稳定性的判定方法和July 稳定判据可知［20］,F1(λ=1)=0 不满足约束条件,即ε1为不稳定均衡点,同理,ε2、ε3均为不稳定均衡点,其中,均衡点ε1表示有2 类LA 在市场竞争中会因为失去市场份额而被淘汰,均衡点ε2和ε3分别表示第1 类和第2 类LA 会在激烈的竞争中被淘汰。将纳什均衡点ε4代入Jacobi 矩阵,对应的特征方程F4(λ)为:

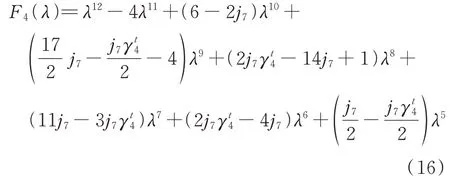
式中:j7=-α2k(1-ω2)L2,t。当均衡点ε4对应的特征方程在满足July 稳定判据的稳定域内时,称其为系统式（11）的稳定均衡点ε*4。在现实场景中,当纳什均衡点同时满足稳定域条件和式（17）的约束条件时,才成为具有实际意义的稳定均衡点。

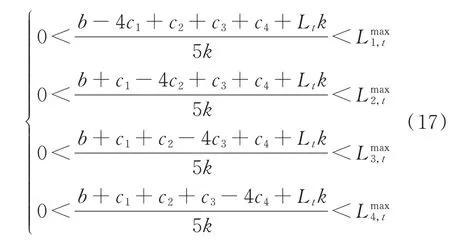
由于居民柔性负荷削减情况受市场电价和补偿价格等因素的影响,随着参数k、b、cn的变动,最大削减量Lmaxn,t也会随之变动；同时,各LA 根据边际利润情况制定投标决策,由于边际利润πn,t是关于参数k、b、cn的函数,故投标量Ln,t也会随着k、b、cn的改变而变动。即参数Lmaxn,t与均衡点解集实际上是存在相互约束关系,但获取该关系的数学模型存在较大的困难。因此,可通过数值解析方法判定是否满足约束条件,若在特定参数下均衡点无法满足该约束条件,则说明系统参数选取不合理,无法使系统达到最优状态,此时可采取牛顿-拉夫逊法进行参数搜寻,重新调节相关参数以满足约束条件。首先,对式（12）建立修正方程:ΔW=-JRΔV,其中,ΔW=[f1f2f3f4]T,ΔV=[ ΔL1,tΔL2,tΔL3,tΔL4,t]T,ΔL1,t至ΔL4,t为系统式（12）近似解的修正量,雅可比矩阵JR是对系统式（12）中各式求偏导数得到的,即

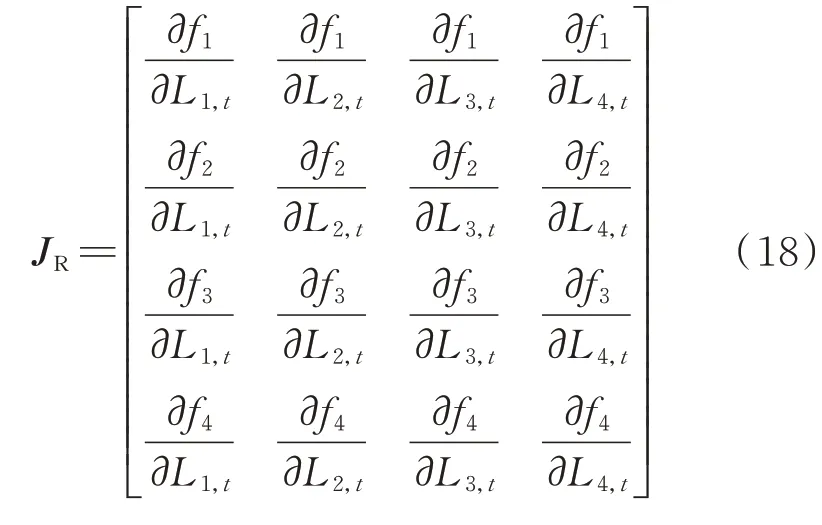
其次,通过求解修正方程得到各修正量ΔLn,t,根据L(i+1)n,t=L(i)n,t+ΔLn,t进行迭代计算,该步骤在满足下方收敛条件前重复进行:

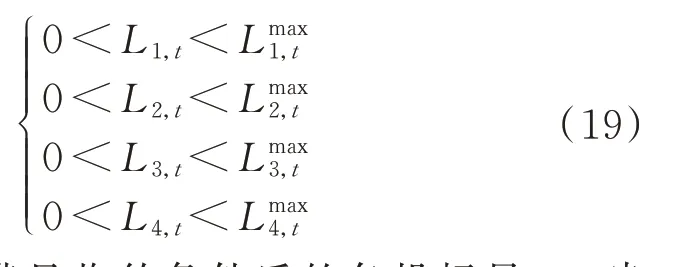
最后,依据满足收敛条件后的各投标量Ln,t建立如下方程组,即

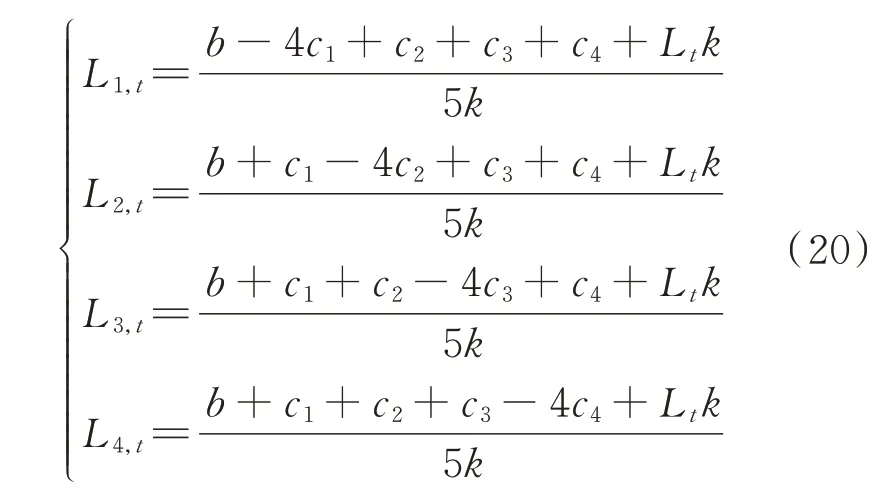
由于该方程组包含4 个方程和6 个未知数,故有多种组合解,可根据市场实际情况选择最贴合的一组解集。实际DR 市场上,可能只存在上述4 类LA中的2 类或3 类参与竞争,其具体建模与分析方法类似,此处不再赘述。

3 DR 市场投标失稳控制策略

当LA 决策调整速度超过阈值范围时,系统会进入分叉混沌状态,此时系统具有不可预测性,各LA 的利润也不稳定,进而导致DR 市场失稳。因此,一旦系统失去稳定,就需要对整个市场实施混沌控制［21-23］。本文将基于延迟反馈控制法对DR 市场投标决策失稳进行控制。延迟反馈控制的主要思想是将系统本身响应信号的部分信息经延迟时间再反馈到系统中,调节控制信号的权重和大小因子来稳定系统输出［24］。考虑如下形式的延迟反馈系统:

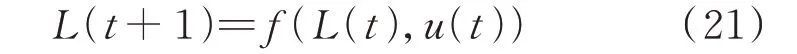
式中:L(t)为在周期t内的状态变量；u(t)为周期t内的控制信号。

利用如下控制信号来稳定系统输出:

矩阵其余各行不变,即可得到第1 类LA 施加控制策略后系统的Jacobi 矩阵,代入纳什均衡点ε*4,求得其对应的特征方程。当特征方程满足July 稳定判据约束条件时,系统处于稳定均衡状态,可求得此时控制因子K的取值范围。其余各类LA 控制决策模型与此类似,此处不再赘述。

4 算例仿真分析

4.1 算例数据及假设

设k=100元/（MW·h2）,b=-2 500元/（MW·h）,Lt初始值为40 MW·h,各LA 在t周期内可削减最大负荷量为3 MW·h,投标量初始值L1、L2、L3、L4分别 为1.5、2、2.9、1.6 MW·h；补偿价格c1、c2、c3、c4分别为550、530、515、520 元/（MW·h）；取延迟参数ω2=0.3,自适应调整系数θ3=θ4=0.2,学习能力指数γ4=0.7,竞争周期t=300 轮,研究调整速度变化对系统动态演化博弈的影响。

4.2 算例结果分析

为分析LA 参与DR 市场竞争的演化过程,本算例分析了各LA 在调整速度α1和α2变化时其投标量和平均利润的动态演化情况,平均利润取300 轮竞争周期利润的平均值。

图1 所示为当第2 类LA 调整速度α2=0.25 时,LA 投标量和平均利润随α1变化的动态演化趋势。如图1（a）所示,当α1在0～0.7 之间变化时,系统运动状态稳定,随着α1不断增大,系统开始分岔,走向混沌状态。如图1（b）所示,第2 类LA 平均利润会在系统分叉之后呈下降趋势,而其他LA 平均利润则呈上升趋势,这意味着混沌现象并非都有害。第1、3、4 类LA 更希望第1 类LA 能增大投标量调整速度,使系统混沌,从而获取更多利润；而第2 类LA 则希望能采取措施控制系统混沌的发展,以确保自身收益。

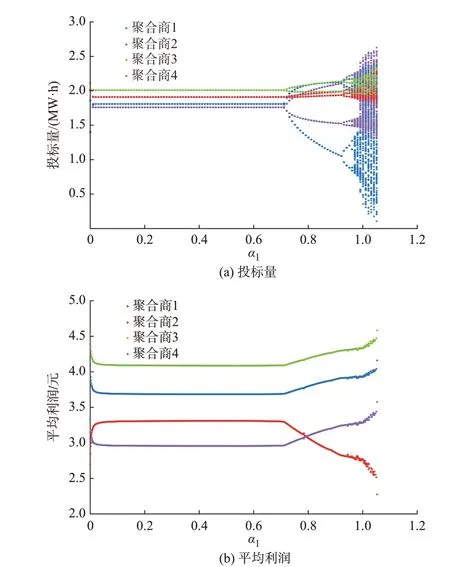
图1 α2=0.25 时LA 投标量和平均利润动态演化图Fig.1 Dynamic evolution diagram of LA bidding quantity and average profit when α2 is 0.25

若第2 类LA 不经市场分析,试图通过增大调整速度以获取更多收益,令α2=0.65,如图2（a）所示,系统从一开始就处于混沌状态,且混沌域变大,并没有改变其演化趋势。如图2（b）所示,随着第1 类LA不断提高调整速度,其他LA 的平均利润皆呈下降趋势,第2 类LA 未能提高自身收益。第3、4 类LA则希望第2 类LA 能降低调整速度以保证自己的收益；虽然第1 类LA 平均利润呈上升趋势,但相较于图1（b）其总体平均利润大小明显下降。基于以上情况,所有LA 都希望能够采取有效的措施控制系统混沌的发展。图3 所示为当第1 类LA 调整速度α1=0.25 时,LA 投标量和平均利润随参数α2变化的动态演化趋势。从图3（a）中可以看出,当α2在0～0.55 之间变化时,系统处于均衡稳定状态,继续增大α2,系统走向混沌状态,继而开始分叉。如图3（b）所示,当系统开始混沌之后,第1 类LA 的平均利润呈明显下降趋势,其他LA 的平均利润则开始上升。第2 类LA肯定希望通过加大调整速度来提升自己的收益,第3、4 类LA 则获得因系统波动带来的收益,但第1 类LA 希望采取措施避免系统向混沌方向演化,以此保证自己的收益。

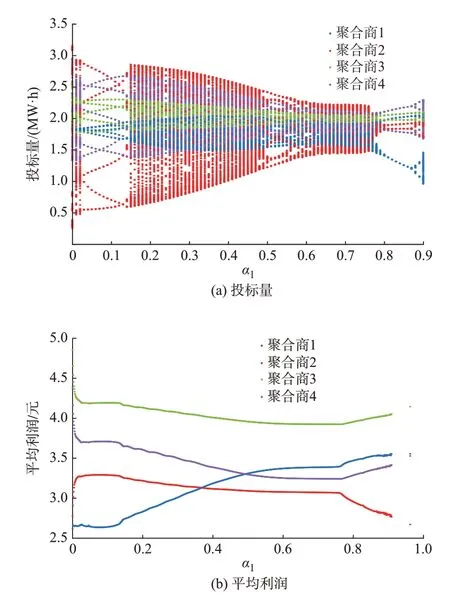
图2 α2=0.65 时LA 投标量和平均利润动态演化图Fig.2 Dynamic evolution diagram of LA bidding quantity and average profit when α2 is 0.65

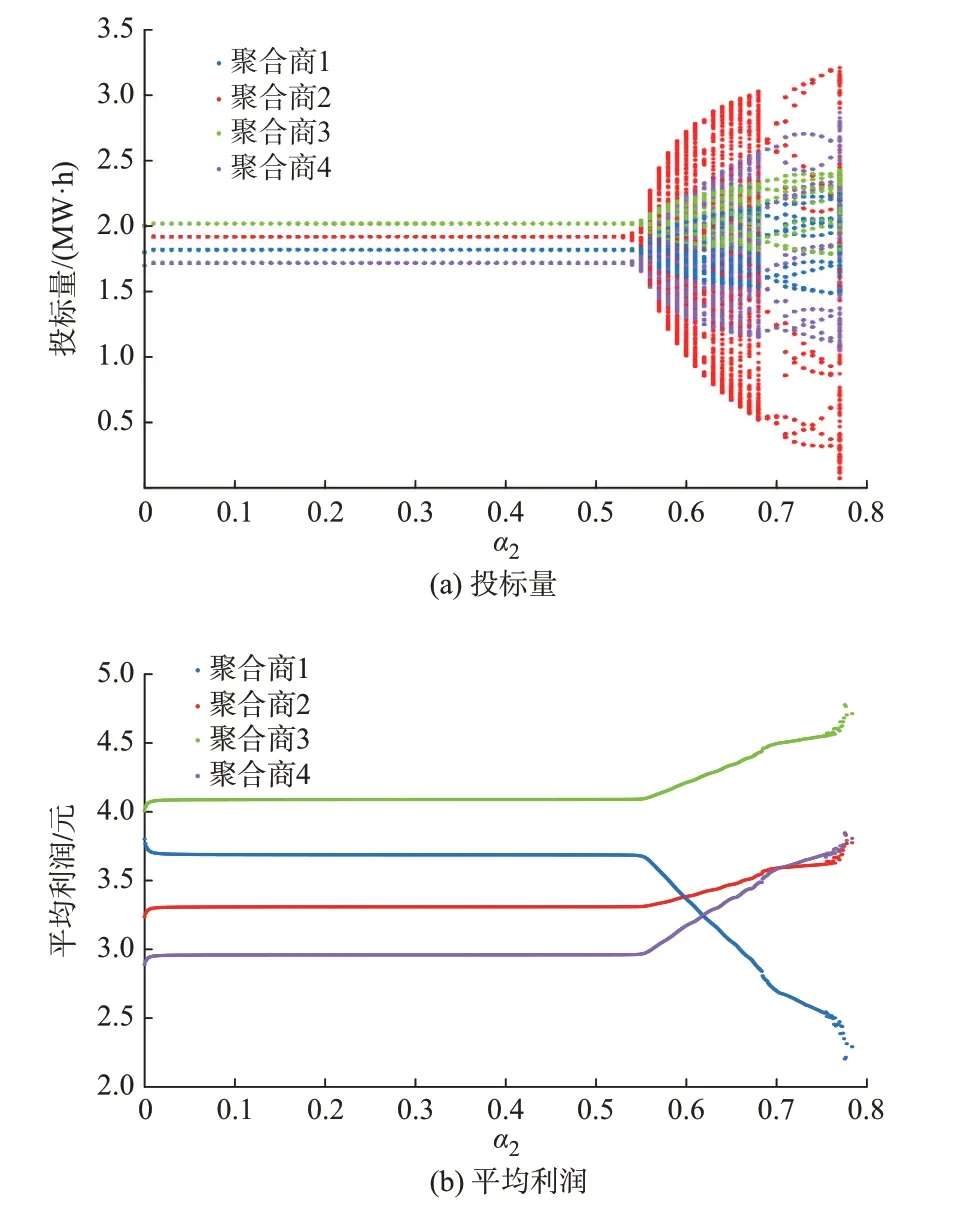
图3 α1=0.25 时LA 投标量和平均利润动态演化图Fig.3 Dynamic evolution diagram of LA bidding quantity and average profit when α1 is 0.25

若第1 类LA 企图增大调整速度来增加自己的收益,令α1=0.65,如图4（a）所示,随着α2不断增大,系统从稳定均衡状态逐渐走向混沌,虽然混沌域变小,但在图4（b）中第1 类LA 的平均利润在系统混沌之后依旧呈下降趋势,第3、4 类LA 的平均利润逐渐上升,第2 类LA 的平均利润趋于稳定。对于第2 类LA 来说,增大调整速度对其意义不大,因此很可能保持调整速度不变,但对于第3、4 类LA 来说,则希望其能够大幅度增加调整速度使自己获得更多收益,第1 类LA 则不愿出现这种结果,故希望能够对系统的混沌状态加以控制,至少在激烈的市场竞争中不被淘汰。

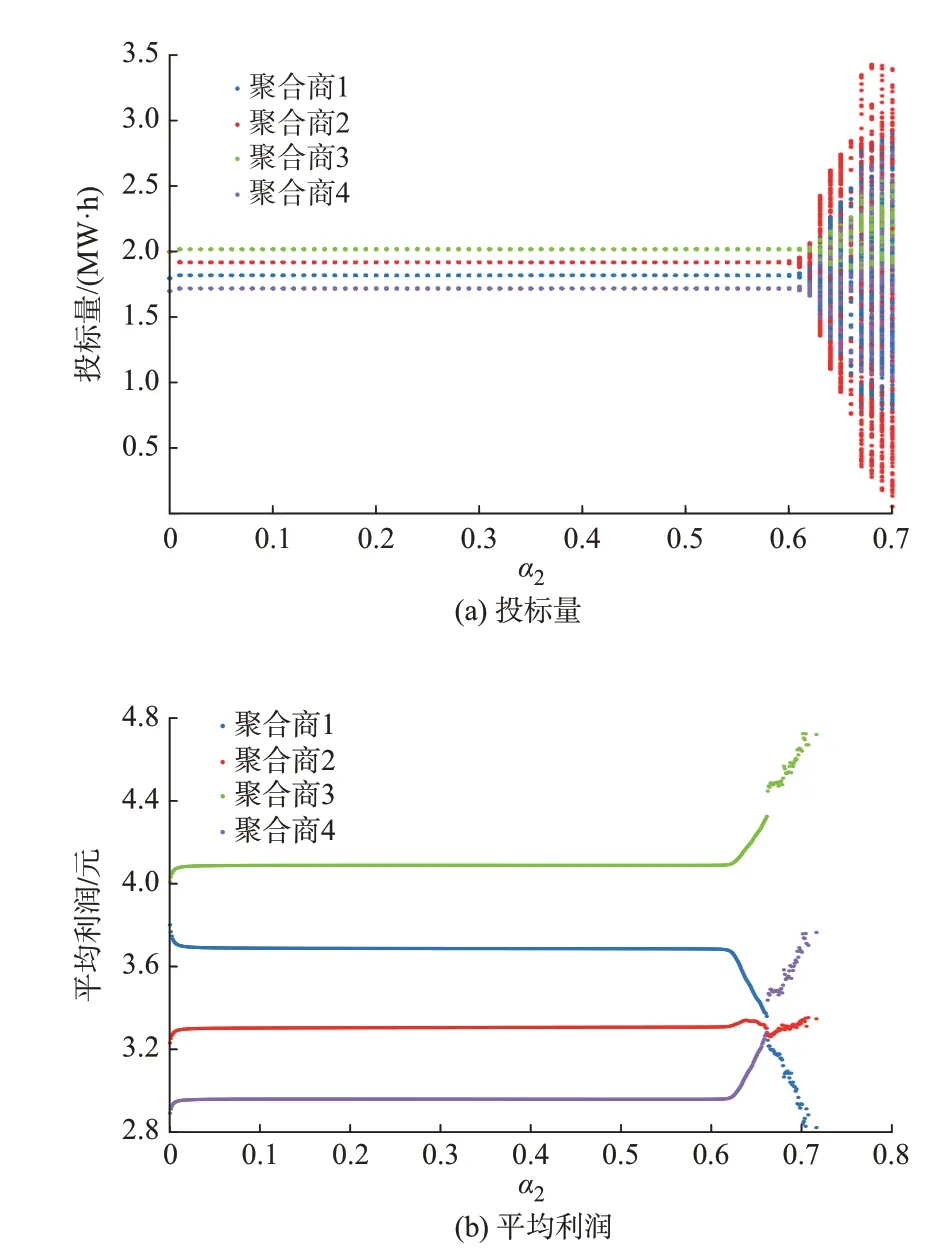
图4 α1=0.65 时LA 投标量和平均利润动态演化图Fig.4 Dynamic evolution diagram of LA bidding quantity and average profit when α1 is 0.65

通过分析以上结果可知,随着投标量调整参数变化,系统会呈现复杂的动力学现象,各LA 收益均存在不确定性。当参数选取在一定范围之内时,系统的纳什均衡点始终不变,即调整参数并不影响系统纳什均衡［25］。同时,混沌现象的出现并非均有害,当调整参数很小时,LA 利润大多趋于均衡稳定状态,而当调整参数增大到一定值时,即系统向分叉、混沌的状态发展,各LA 利润呈现不确定性。即维持其他条件不变,适当地调整投标量速度可以给市场带来好处,大幅度的调整在一定程度上会扰乱系统的稳定,对于每个LA 而言都是不希望看到的。因此,若不是对市场和竞争对手进行准确的分析,而是盲目通过增大调整参数来使自己获得更多收益,则最后不可避免地会落入“囚徒困境”。

4.3 混沌控制结果

当DR 市场失稳后,运用延迟反馈控制法对系统实施混沌控制,模拟系统随控制因子K变化的动态演化过程,验证控制方法的有效性。

图5（a）为图1（a）中第1 类LA 实施延迟反馈控制策略后,各LA 投标量稳定到均衡解的过程。考虑到参数的大小可能会影响控制效果,为验证控制方法的有效性,在选取参数代入控制系统时,选择图1（a）中导致系统出现混沌现象的最大边界值,即α1=1.05,α2=0.25。如图5（a）所示,实施反馈控制后,即使α1取最大边界值,但随着控制因子K的不断调整,系统可逐步稳定于均衡状态,混沌分岔行为被有效抑制。图5（b）为图4（a）中第2 类LA 实施混沌控制后系统的动态演化趋势。同样,将系统处于混沌边界状态下的各参数代入控制模型,即α1=0.65,α2=0.7。如图5（b）所示,引入延迟反馈控制后,各LA 的投标决策量在博弈过程中逐步稳定于纳什均衡解。对比图5（a）和（b）可知,在不同α1、α2值下均可通过调节K值使系统达到控制效果；对不同类型LA 实施混沌控制时,虽然各类LA 参与DR市场时采取不同的投标策略,但通过延迟反馈控制,系统最终都会稳定到同一均衡解,这也从侧面验证了控制策略的有效性。

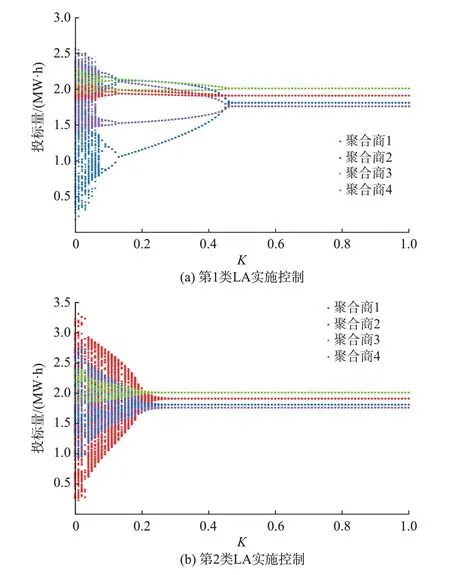
图5 LA 实施控制策略时的系统动态演化趋势Fig.5 Dynamic evolution trend of system when LA implements control strategy

5 结语

本文基于4 类常见的有限理性决策模型构建了LA 参与DR 市场的投标非合作博弈动态模型,并对模型的均衡点和稳定域进行了分析。通过数值仿真研究了LA 投标量调整速度的变化对模型稳定性的影响。研究结论如下:

1）单个LA 决策行为的动态变化会影响整个投标市场,随着其投标量调整速度的增大,系统会进入分叉和混沌状态。

2）对于LA 而言,并不是投标量调整速度越大利润就越大,随意增大调整速度可能会导致系统的混沌域扩大,影响所有LA 的利益。

3）延迟反馈控制法可以对系统实施有效的混沌控制,使各LA 的投标量稳定在均衡状态。

本文暂未考虑调度侧负荷约束对LA 参与市场投标决策的影响,以及在非线性成本情况下各类LA 的竞争结果等,这些均有待进一步研究。

本文研究工作得到了江苏省高等学校自然科学研究面上项目(20KJB470024)以及江苏省研究生实践创新计划项目(SJCX22_0577)的支持，特此感谢！