基于毫米波雷达获取料堆DEM的插值方法研究

孔德明，曹 帅，沈 阅，周逸人

(1. 燕山大学 电气工程学院， 河北 秦皇岛 066004； 2. 河北燕大燕软信息系统有限公司， 河北 秦皇岛 066004)

1 引 言

在新型智能化散杂货港口中，散杂货料堆的快速、高效的无人化机械堆取是港口未来的发展方向，全天候、快速、便捷和稳定地得到料堆的离散点云数据和插值构建数字高程模型(digital elevation model, DEM)是实现堆取料机全自动化和体积测量的关键。

在现有的技术手段下，由于料堆形状过高、纹理特征贫乏和材质反射率低等特性，如何快速、高精度获取被测物体表面的三维信息是测量问题的重点[1]。离散点云数据的获取主要有激光测量[2～4]、计算机视觉测量[5～7]等。杨德山等[8]提出采用手提测量系统，通过围绕堆体行走时激光扫描仪动态测量堆体表面的三维数据；张望等[9]提出操作者仅需手提扫描设备绕行被测货堆一周便可快速获得细节特征明显的三维模型的方法；吕小宁等[10]基于断面的激光精细测量系统，对某地下储油洞室群进行了现场实验，得到储油洞室的三维数据；赵其杰等[11]提出激光扫描传感器在传动平台驱动下，沿着堆积物料一侧运动并进行大范围扫描采集被测点的空间坐标信息。但是在露天港口的工作环境下，基于激光和视觉的方法不能够在雾雨雪天气以及沙尘环境下正常工作，因此，新的研究方法应能克服恶劣环境的影响，使得自动化堆取料机系统随时能够正常获取离散点云数据并且能够达到一定精度。

77 GHz毫米波雷达具有频带宽、波长短、体积小、功耗低和穿透力强等特点，相比于激光红外探测，其穿透性强的特点可以保证雷达能够在雾雨雪以及沙尘环境工作，受天气影响较小[12]。随着毫米波雷达技术的不断发展，在大型散杂货料堆的测量应用场景中，毫米波雷达能够像二维激光雷达一样通过扫描获取得到目标的位置信息。

对在港口中获取料堆DEM的研究已有许多报道，毫米波雷达点云数据的逐点插值是构建DEM最有效途径之一[13]，常见的插值算法有：普通Kriging (ordinary kriging，OK)插值算法[14,15]、反距离加权(inverse distance weighted，IDW)插值算法[16]、基于三角剖分的线性插值(triangulation with linear interpolation，TLI)算法和自然邻域(natural neighbor，NN)插值算法[17]等，针对测量装置获取的毫米波雷达离散点云数据存在空洞、不均匀和散乱度高的问题，利用现有的插值方式对毫米波雷达点云进行插值，得到的可视化模型和DEM精度较低，故应改进现有逐点插值方法以获取更高精度的料堆DEM。

目前，关于基于毫米波雷达获取料堆表面几何信息的研究报道较少，本文在文献[8,9]利用激光扫描获取料堆离散点云数据的基础上，提出了一种利用77 GHz毫米波雷达、差分北斗和角编码器等传感器获取料堆表面离散点云数据的方法，分析离散点云数据误差来源，通过改进Kriging插值算法提高插值精度，一方面是可以补足缺失的空洞，另一方面是通过对插值区域的控制得到均匀的数据，采用交叉验证的方式对比分析不同离散点云数据插值方法的插值精度。实验结果证明：本文提出的装置和方法具有很好的环境适应性、稳定性、便捷性和低成本的特点，能够满足实际的项目需求。

2 获取料堆离散点云数据

2.1 数据采集

2.1.1 基于77 GHz毫米波雷达数据采集装置

以堆料机为例，毫米波雷达传感器安装在出料口前方，获取料堆表面坐标信息；双天线差分北斗传感器安装在回转平台上，获取回转中心在堆场内的位置数据；角编码器获取堆料机大臂的俯仰角和回转角数据。77 GHz毫米波雷达是能够在全天候场景下快速感知0～200 m范围内周边环境内目标信息的长距离双波束雷达，远距离波束的扫描范围为水平方向45°，近距离波束的的扫描范围是60°，并且可以72 ms完成一次近距和远距的测量，毫米波雷达工作在集群模式，其扫描面垂直向下扫描料堆的横截面，能够返回测量点的横向距离、纵向距离、雷达的反射截面积、虚警概率等信息，其扫描示意图如图1所示；采用精确到cm级的差分北斗定位传感器；采用精确到0.15°的角编码器。

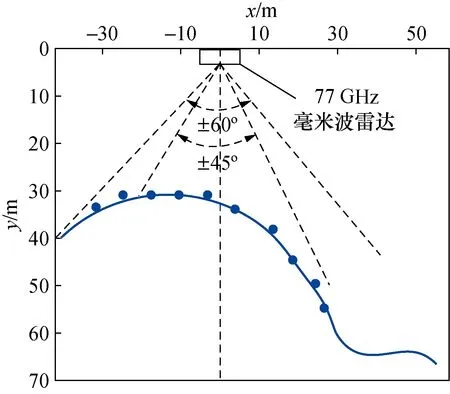
图1 毫米波雷达扫描示意图Fig.1 Schematic diagram of millimeter wave radar scanning

2.1.2 堆场模型

在长方形露天的自动化散杂货堆场，建立堆场全局坐标系O0-X0Y0Z0，以水平向北为Y0轴，水平向东为X0，Z0轴垂直于长方形堆场；定义堆料机在堆场轨道上的位置为堆料机坐标系O1-X1Y1Z1；其中X1O1Z1平面随着大臂的转动进行转动；定义毫米波雷达坐标系O-XYZ。料堆的堆场模型由图2所示，θ是大臂的俯仰角，L是毫米波雷达到回转中心的长度，H是回转中心到堆料机坐标系原点的高度，φ是大臂的回转角。

图2 堆场料堆模型示意图Fig.2 Schematic diagram of stockyard model

将毫米波雷达获取到的数据P(x,y,z)、北斗定位数据和角度传感器数据通过公式(1)解算到堆场坐标系O0-X0Y0Z0，得到料堆表面的三维数据P0(x0,y0,z0)。

(1)

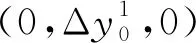
2.1.3 测量过程

测量过程：通过PLC控制堆料机的大臂俯仰到一定角度，以不同的回转角往复低速走行采集料堆表面的几何信息，同时存储北斗传感器和角编码器的数据，将多传感器数据发送到数据处理服务器，通过对多传感器的数据解算和坐标系转换得到料堆多组三维数据，对多组点云数据进行滤波和精简，之后进行配准得到料堆点云数据，采用点云数据投影区域的逐点插值算法获取均匀的点云数据，料堆DEM获取过程如图3所示。

图3 料堆DEM模型获取过程Fig.3 Stock model acquisition process diagram

3 Kriging插值算法及其改进

3.1 普通Kriging插值算法

将采集到的离散点云数据投影到二维平面并求取凸包，根据情况对凸包内区域划分出网格点，生成查询点，查找到查询点周围已知高程值的点，通过普通Kriging插值算法得到查询点的高程值。目前已有学者研究基于普通Kriging算法的点云数据的插值方法[18]，普通Kriging插值算法原理如下：

对于查询点附近的n个临近点t1,t2,t3,…,tn，其观测值为w(t1),w(t2),w(t3),…,w(tn)，对于查询点t0的估计值可以通过一个线性关系来估值：

(2)

式中λi为权值。

由于Kriging插值是一种无偏最优化的插值，无偏性和最小化方差是确定λi的两个条件如下：

(3)

当区域的变量属于二阶平稳假设和本证假设，由公式(3)的两个条件可推导Kriging方程组为

(4)

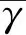
半方差函数模型γ(h)通过式(5)进行计算，

(5)

式中：N(h)是临近点的点对数；h是滞后距；w(ti)、w(ti+h) 分别是ti和ti+h位置的观测值。

常见的拟合半方差函数模型有球状模型、高斯模型、幂函数模型、空穴函数模型等，可作为半方差函数的球状函数模型：

(6)

式中：c0是块金值；a是变程；c是拱高。

3.2 基于量子化鸽群优化的Kriging插值算法

由于毫米波雷达点云数据散乱程度较大，造成Kriging插值算法拟合半方差函数时精度不高，所以采量子化鸽群算法[19,20]优化拟合半方差函数。基本鸽子群优化算法包括地图指南针算子和地标算子两部分。地图和指南针算子是模仿太阳和地球磁场这两种导航工具对鸽子的影响。鸽群中第j只鸽子在第s代的速度信息和位置信息的更新策略如下：

Vj(s+1)=e-RtVj(s)+ru[(Ggb(s)-G(s)]

(7)

Gj(s+1)=Gj(s)+Vj(s+1)

(8)

式中：R是罗盘算子，取值范围是0到1；Vj(s)是鸽子的速度信息；Gj(s)是鸽子的位置信息；ru表示随机数；Ggb(s)鸽群中所有鸽子的全局最优的位置。

当迭代次数达到一定值时停止地图指南针算子的工作，进入地标算子的迭代过程中继续工作，每一次迭代鸽子数量减半，位置更新策略为

Np(s)=Np(s-1)/2

(9)

(10)

Gi(s)=Gi(s-1)+ru(GC(s)-Gi(s-1))

(11)

式中：Np是当前鸽子数量；F(Gi(s))是自适应度函数；GC(s)是鸽子群的中心且被当做地标；ru是0到1之间的随机数。

量子化鸽群优化算法引入实数的量子表示和量子旋转门。一个量子可以通过“0”和“1”态表示，量子位状态被表示为

|ψi〉=αi|0〉+βi|1〉

(12)

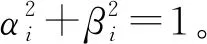
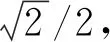
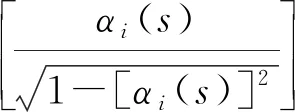
(13)

(14)

式中：Δθ是旋转角度；ε是约束参数，防止量子困在状态“0”和“1”。

4 离散点云数据的误差来源以及插值算法评价指标

4.1 误差来源

影响料堆表面离散点云数据准确性的原因主要有4类：第1类是堆取料机在采集数据的过程中会发生轻度的震动，造成扫描点位置偏差；第2类是传感器的测量误差，主要有毫米波雷达的测距和测角误差，角编码器的测角误差，差分北斗传感器的定位误差以及不同测量数据时间同步误差等；第3类是测量设备安装的误差，主要有毫米波雷达的安装误差角和位置偏移量等；第4类是料堆的形状不同可能会造成料堆表面数据缺失，造成插值误差。其中，第3类测量设备的安装误差可通过采集数据的直线特征提取并结合结构参数列出约束方程求出初始状态标定值，再利用初始状态值和测量过程中获取的系统位置姿态变化量实现在线标定和测量。

4.2 评价指标

采用交叉验证的方式评价不同的逐点插值算法的精度以及料堆表面的还原度，对处理之后的离散点云数据采样80%的点云数据作为内插样本数据，20%的点云数据作为实测数据来验证插值精度。误差的大小通过高程值的差异进行反应，通过均方误差(MSE)、均方根误差(RMSE)和预测吻合度R2评价插值的精度，计算公式如下：

(15)

(16)

(17)

5 算法验证

5.1 点云数据统计信息

利用上述算法，在某煤炭港务有限公司的自动化改造项目中进行测试应用，用于料堆表面点云数据获取并通过插值算法得到料堆的DEM。对于80 m宽的堆场，堆料机的大臂俯仰角达到12.50°，回转角以65°、55°、40°和30°全自动走行，同时采集并存储多个传感器的数据，融合解算后得到离散点云数据。对数据处理之后共得到6组料堆离散点云数据，其每平方米点的个数在25个左右，由峰度可知料堆1和料堆2的高程值更接近正态分布，料堆3和料堆4稍微陡峭一些，由偏度可知6个料堆的高程值分布都右偏，料堆都有局部的狭长空洞，且形状和面积都不相同，统计信息包括离散点云数据中点的个数，离散点云数据的投影凸包的面积stt、最大高程值hmax、平均高程值hv、高程值的标准差hσ、高程值的峰度、高程值的偏度。料堆的离散点云数据详细的统计信息见表1。

5.2 不同插值方法得到的DEM

将基于毫米波雷达多传感器融合得到料堆1的离散点云数据经过去噪、去除地面点、精简和配准之后,得到具有狭长空洞的离散点云数据见图4中的原始点云数据。选择0.1 m分辨率的格网尺寸，采用的改进的Kriging插值算法(improve ordinary kriging，IOK)、OK、IDW、TLI和NN插值算法获取DEM如图4所示，图4中的插值算法都能够填补原始点云数据的漏洞得到完整的DEM，它们是获取地形地势、建筑物DEM的主要方式。

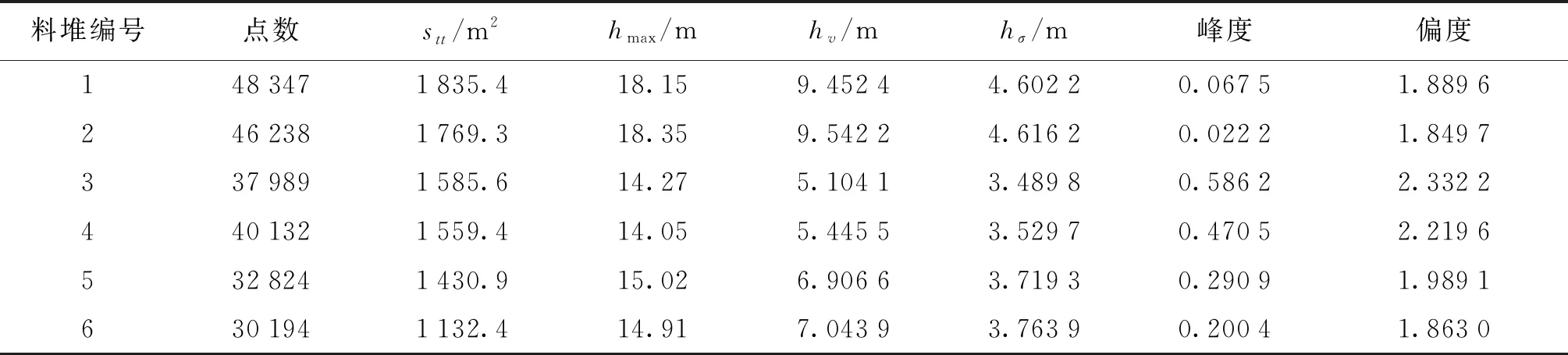
表1 料堆离散点云数据的描述参数统计Tab.1 Description parameter statistics of the discrete point cloud data of the stockpile

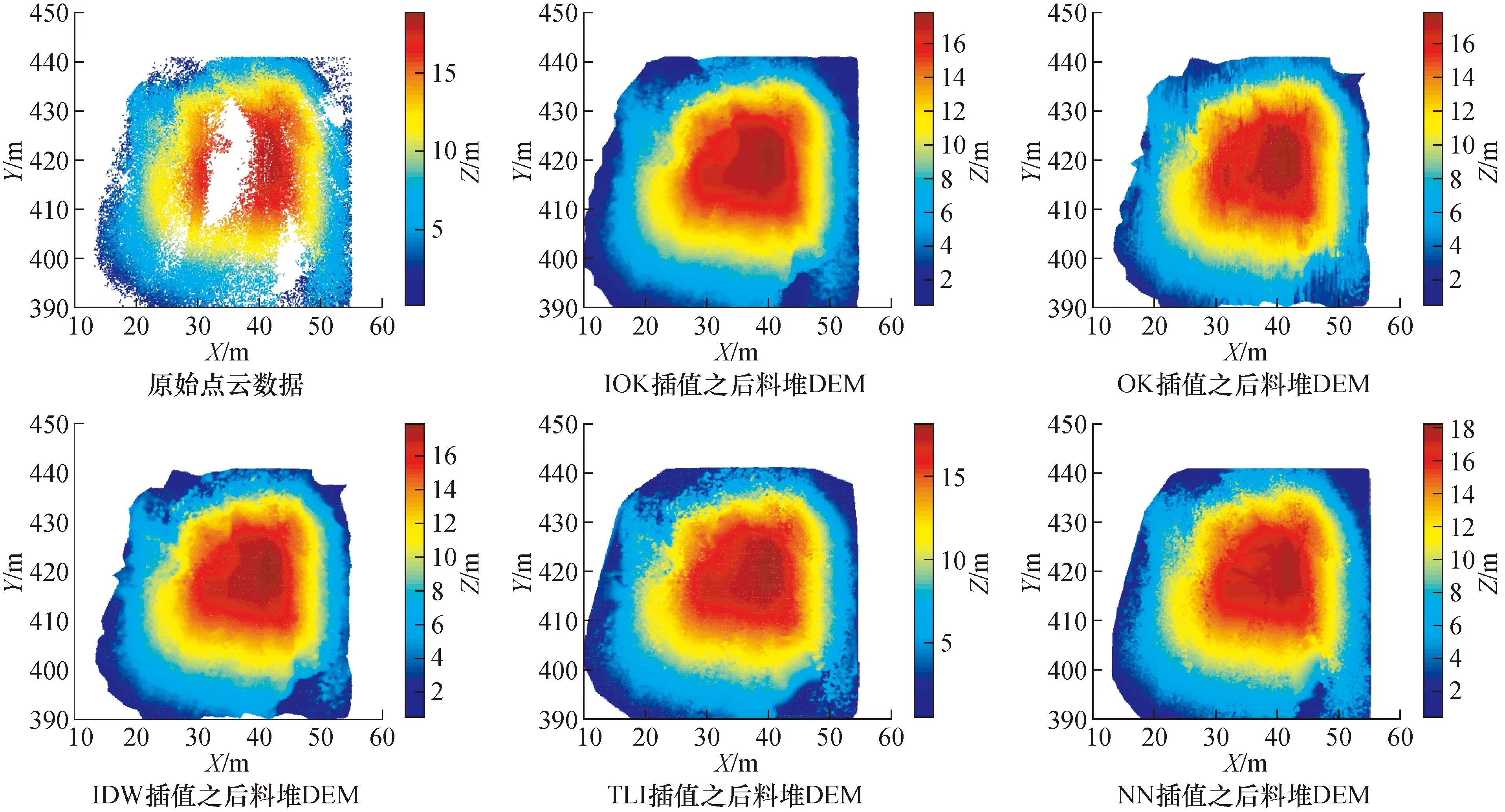
图4 不同插值方法得到的DEMFig.4 Elevation model obtained by different interpolation methods

5.3 不同插值方法精度分析

对5种的离散点云数据插值算法进行参数优选，IOK初始以地图和指南针算子为导向的迭代次数设置为70，地标算子为导向的迭代次数为30次，种群数量为80；IDW插值算法的幂次设置为2次，搜索25个临近点；TLI插值算法以Delaunay三角化准则构造三角形为基础进行插值；NN插值算法以Delaunay三角化构造Voronoi多边形为基础进行插值。为了评价不同插值算法的插值精度，采样料堆离散点云数据的20%当作真值，得到不同料堆的不同插值算法的有效性交叉验证结果，6组不同料堆的均方误差MSE和均方根误差RMSE交叉验证结果如图5、图6所示。

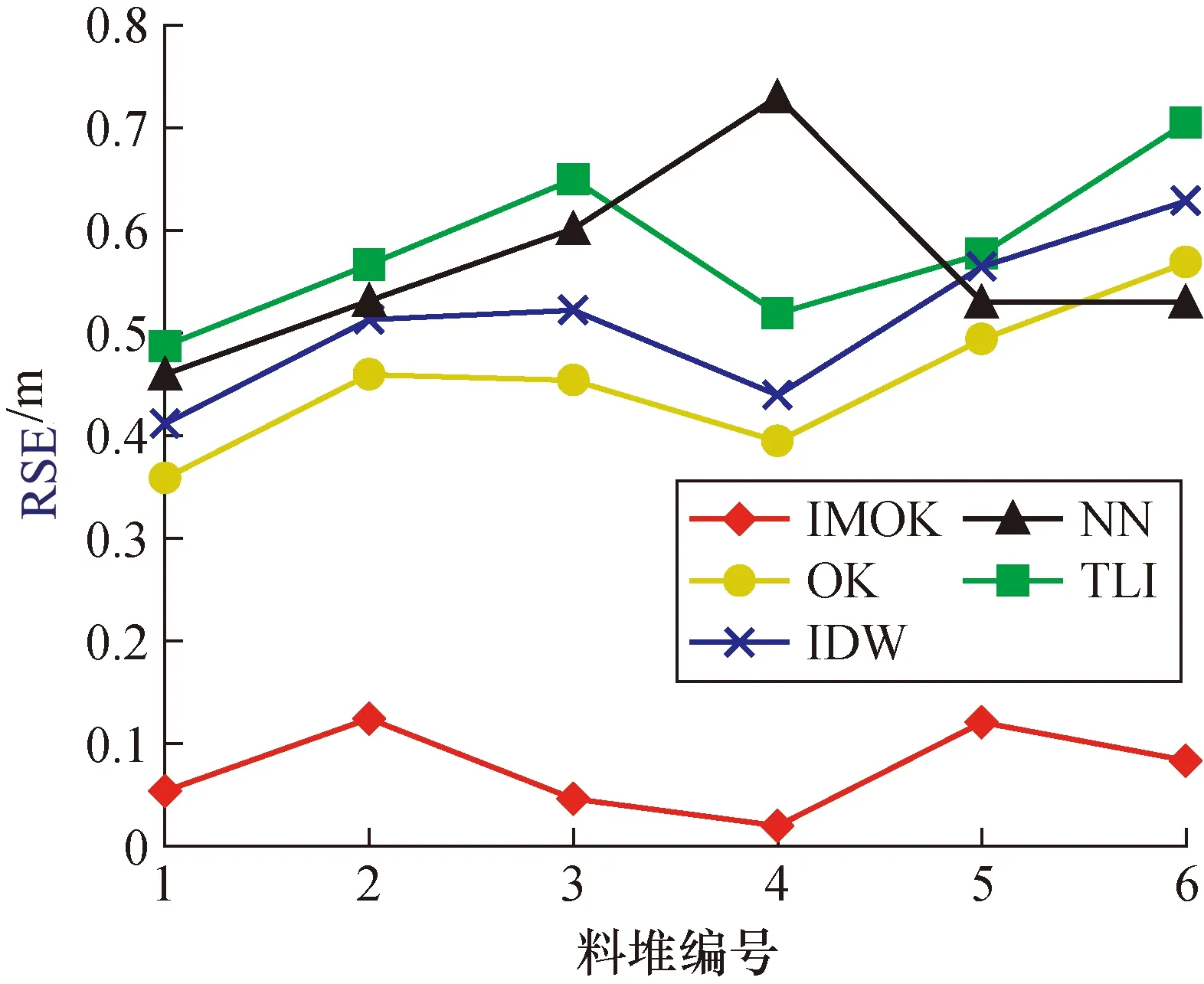
图5 均方误差的结果Fig.5 Results of mean square error

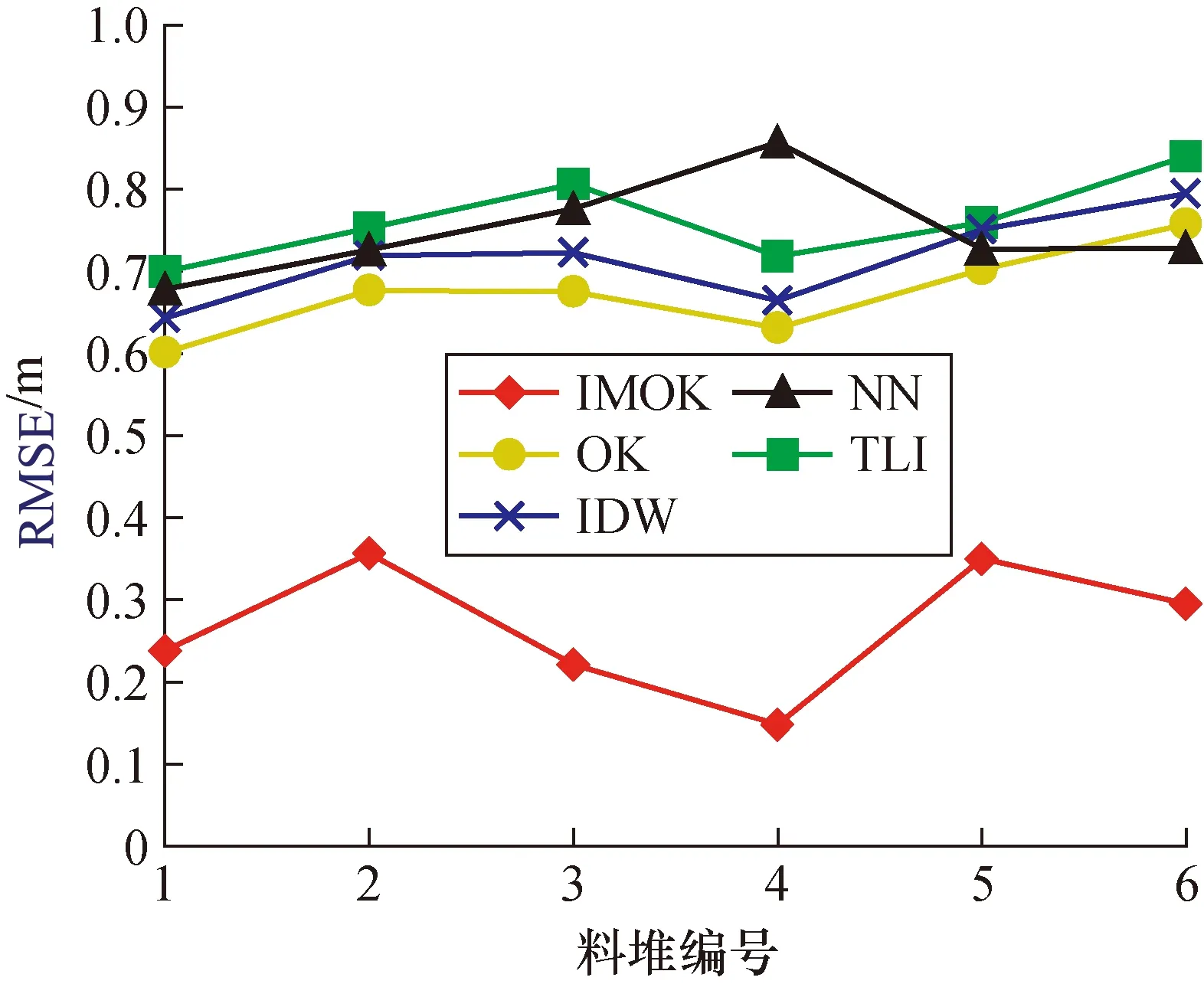
图6 均方根误差的结果Fig.6 Results of root mean square error

由图5和图6所示的6组数据可知IOK算法RMSE低于0.37 m，MSE低于0.14 m, 预测吻合度R2达到0.984以上；OK插值算法获取的6组数据的RMSE大于0.5 m，MSE大于0.32 m，R2低于0.977 7，其中4组数据R2低于0.96；IDW、NN、TLI的插值算法获取的交叉验证结果较差，RMSE大于0.5 m，R2低于0.958 5。

由图5和图6所示的MSE和RMSE说明，基于毫米波雷达获取的料堆离散点云数据采用不同的逐点插值算法获取料堆DEM的有效性依次是IOK插值算法、OK插值算法、IDW插值算法、NN插值算法、TLI插值算法，其中IDW、TLI、NN算法误差浮动较大，可知处理不同料堆的离散点云数据时IOK插值算法都能取得较好的效果，具有较好的稳定性，IOK插值算法的RMSE稳定在0.2 m到0.4 m之间，计算每一组数据的IOK插值算法和OK插值算法RMSE的相对偏差，可知IOK的RMSE相比OK算法降低了39.9%，改进后的插值算法更加适合毫米波雷达点云数据获取DEM。

6 结 论

在某煤炭港口的自动化堆取料系统实际应用毫米波雷达、差分北斗传感器和角编码器传感器集成的技术，全自动全天候获取料堆的DEM，基于毫米波雷达取点云数据的方式可以弥补雨雪以及大量灰尘工况下激光和视觉方式测量的短板；插值算法的有效性依次是IOK插值算法、OK插值算法、IDW插值算法、NN插值算法、TLI插值算法，改进后的Kriging插值算法提高了毫米波雷达点云数据的插值精度，其RMSE低于0.37 m，MSE低于0.14 m，RMSE相比OK插值算法降低了39.9%，R2达到0.984以上；得到的DEM能够满足堆取料机自动化项目对精度的需求。