前缘磨蚀对风力机叶片材料特性影响的数值研究

甄琦，张寅，陈松利，闫彩霞，万大千，孙凯

(内蒙古农业大学能源与交通工程学院，内蒙古呼和浩特 010018)

0 前言

风能作为一种可再生资源，我国储量丰富[1]。内蒙古和甘肃作为我国风能资源区适宜风力发电[2]，但西北地区是每年沙尘暴频繁发生的地区[3]，风沙会对风力发电机组的设施构成冲蚀，尤其是对作为风力发电机组关键部件的叶片造成的冲蚀尤为严重，机组的运行效率和叶片的质量相关度较高[4]。被风沙冲蚀的风力发电机叶片不仅结构强度和寿命都将降低，其叶片翼型的最大相对厚度、弦向长度等几何参数也会被改变[5]。通过对叶片进行基于有限元法的载荷数值分析，探究叶片的疲劳寿命并诊断故障发生的原因，可以降低故障产生的概率和提高故障诊断的效率[6]。

综上所述，风力发电机组在有风沙冲蚀的环境下长期运行，前缘部分损伤严重，容易产生重大的安全隐患。近些年国内学者使用有限元方法，不仅研究风沙对叶片的冲蚀机制，还研究叶片在各种复杂载荷下的结构强度以及规律；基于所得应力应变数据结合线性疲劳理论，还可以估计叶片的疲劳寿命。有限元方法成为叶片结构强度设计和优化最主要的方法之一。因而基于有限元方法对前缘冲蚀受损叶片进行分析，对于叶片设计和维护十分重要。

本文作者基于有限元分析方法分析不同冲蚀程度的叶片在不同载荷条件下的应力、位移、固有频率。该研究一方面填补了风蚀叶片前缘载荷数值分析的空白，另一方面对叶片工艺的提升有重要的参考价值，所以在风沙环境下对风力发电机叶片前缘磨蚀载荷进行分析和研讨很有意义。

1 叶片载荷分析及数值方法验证

1.1 叶片主要载荷分析

因自然界中的风运动缺乏规律性，所以风力发电机叶片在运行过程中所受到的载荷也是复杂多变的。文中讨论的对叶片产生影响的载荷主要分为气动力、离心力、重力载荷，不考虑其他对叶片影响较小的随机载荷。

1.2 数值方法验证

通过对文献[19]中的数值结果进行验证，以确保数值计算方法的正确性。使用文献[20]中的1.5MW风力机叶片按相似理论设计叶片模型，将该叶片按照原点缩放长度为1 m，与作者研究的叶片长度和设计风力机容量一致，具有较高的参考价值。

建立如图1所示计算域，对旋转域叶片的网格进行细化，使用CFX-静力学模块进行流固耦合分析，计算风速为10 m/s、风轮转速为120 r/min时风轮的应力值。将模型导入瞬态动力学模块进行力学分析，设置原文材料参数，对风轮模型进行非结构化网格的划分。对风轮添加重力载荷、离心力载荷，并在轮毂处施加约束，并设置风轮模型的各个面为流固耦合面，如图2所示。

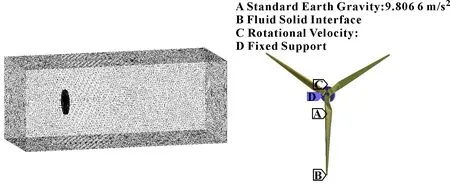
图1 计算域网格 图2 设置载荷约束

当计算达到收敛后，查看风轮的应力分布云图，如图3(a)所示。并提取叶片以X轴为正方向逆时针转30°时，沿叶展方向的应力值，与原文数据进行对比，如图3(b)所示。经过对比，该数值方法较为可靠，满足此课题的需求。

图3 风轮的应力分布云图及与文献[19]中数据对比

2 冲蚀叶片有限元分析

采用多种算例进行研究，经过对比，单向流固耦合和双向流固耦合对叶片进行静力学分析结果相差不大，故选用单向流固耦合的方式来进行分析。

2.1 建立冲蚀叶片模型

引用文献[21]中经过相似及量纲一化处理之后的叶片模型，半径0.82 m，风轮直径2 m。如图4(a)为叶片实体，图4(b)为叶片模型。叶片上受到风沙冲蚀的尺寸引用文献[22]中所述，风沙冲蚀对叶片产生的磨蚀厚度为最大厚度的23%，深度最大为弦长的13%。而选择的磨蚀凹槽的磨蚀深度最大为4%。经计算，布置如表1所示磨蚀凹槽尺寸，同时设立3个磨蚀深度较为严重的尺寸。表中：h为冲蚀产生的深度；c为最大弦长；t为冲蚀产生的厚度；tc为最大厚度。

图4 风机叶片实物和模型

表1 冲蚀尺寸

在SolidWorks中对叶片进行冲蚀模拟，通过拉伸切除、线性阵列等操作，建立如图5所示冲蚀叶片模型。

图5 叶片冲蚀模型

2.2 CFX流体计算域设置

设置计算域的参考大气压为1个大气压，选择标准的κ-Epsilon模型，该模型计算精准且能较快达到收敛；设置Y轴负方向为来流风的方向，入口条件为速度入口，出口条件为压力出口，相对压力为0 Pa。网格的属性默认为CFX，采用Mesh Sizing自适应网格划法，设置计算域网格大小为30 mm，并对叶片模型的网格细化；设置叶片网格大小为5 mm。设置完毕进行网格划分，见图6，共生成网格2 123 085，生成节点398 445，Mesh Metric为0.837 22。对Solver control进行设置，选择最高精度，最小迭代次数为100次，最大迭代次数为2 000次。计算完成后查看叶片在12 m/s时迎风面及背风面的压力云图，如图7、图8所示。

图6 计算域网格

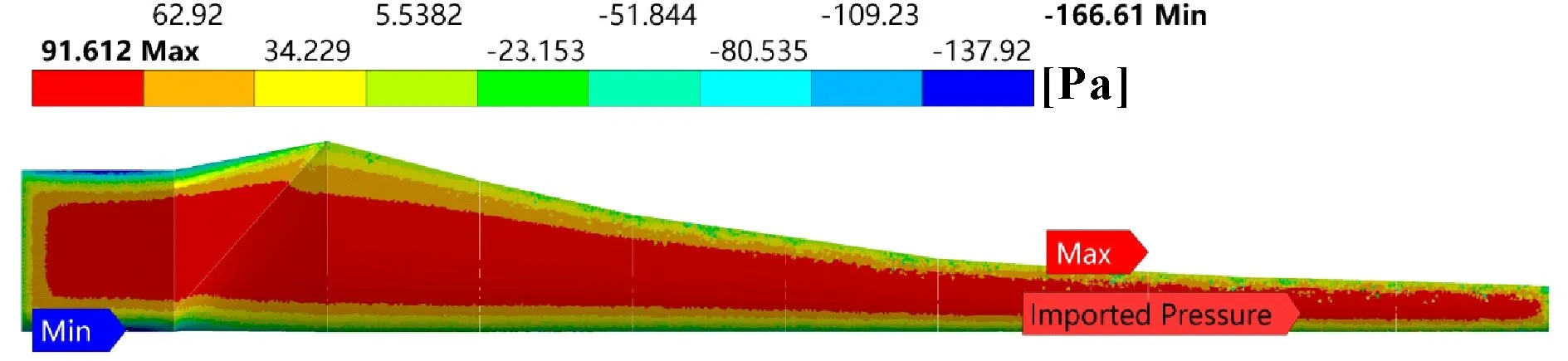
图7 迎风面压力云图

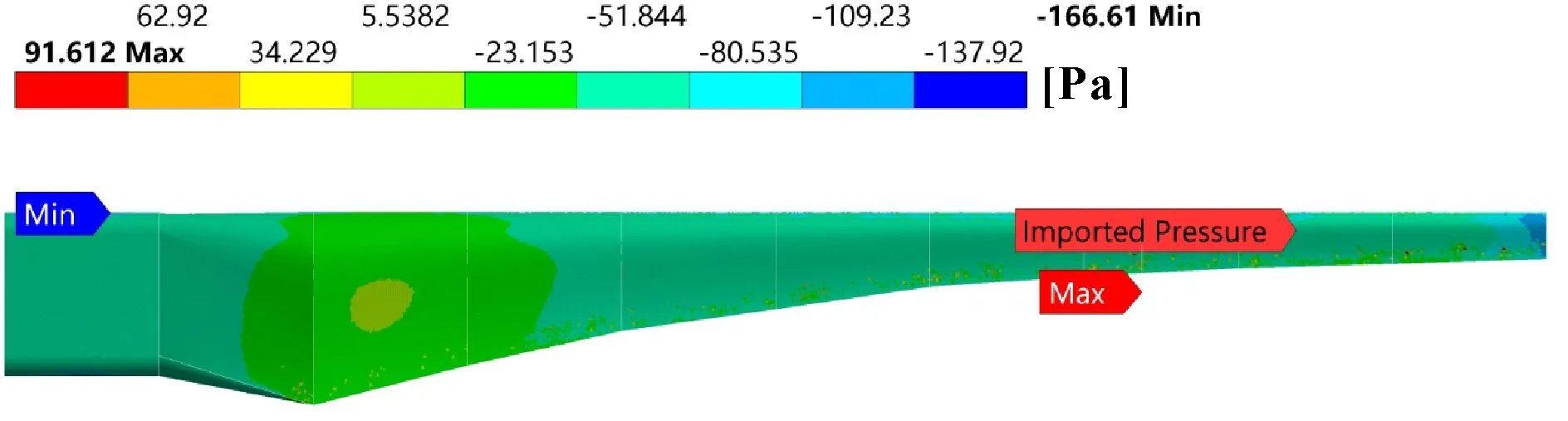
图8 背风面压力云图

2.3 静力结构计算设置

此次研究主要选择两种材料来对比分析，分别为樟子松和环氧树脂。材料的力学性能如表2所示。

表2 樟子木、环氧树脂的力学性能

设置完材料对冲蚀叶片模型进行网格划分，以1 mm×1 mm冲蚀程度的叶片为例，设置网格属性为Mechanical，叶片表面单元尺寸设置为2 mm。经测试2 mm单元尺寸可以兼顾计算的速度和精准度。使用Sizing对叶片冲蚀处的网格进行细化，设置冲蚀处网格单元大小为0.1 mm，设置完进行非结构化网格的划分。图9为叶片整体网格，图10为冲蚀处网格，共生成网格数量1 010 169，网格节点数1 556 633，Mesh Metric为0.773 54。

图9 实体网格

图10 冲蚀处网格

经过流固耦合计算后得到气动载荷施加在整张叶片上，添加重力为+Z方向，添加顺时针的离心力，旋转中心为原点，在叶根处添加固定约束，如图11所示。

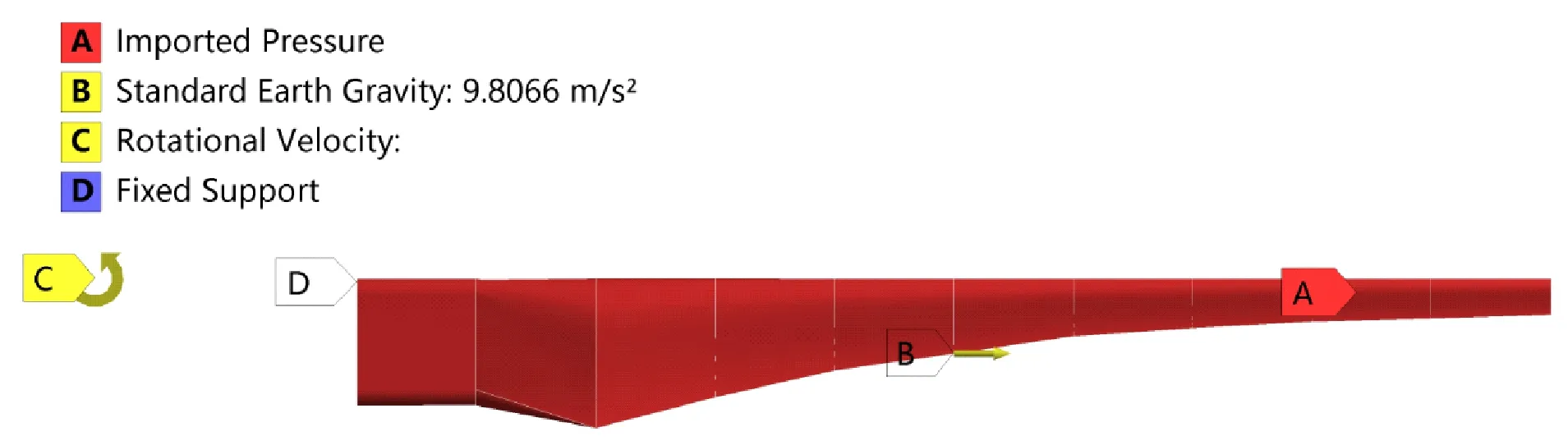
图11 设置载荷约束

3 数值计算及结果分析

3.1 应力分析

设置3种工况：工况1，风速为12 m/s，风轮转速为330 r/min；工况2，风速为12 m/s，风轮转速为550 r/min；工况3，风速为25 m/s，风轮转速为550 r/min。

如图12—图14为环氧树脂叶片在工况1条件下，冲蚀程度从1 mm×1 mm至4 mm×4 mm应力分布云图，从3张图对比可见，随着冲蚀程度的增大，叶片出现最大应力的位置从叶片根部转移到叶片前缘冲蚀受损位置。

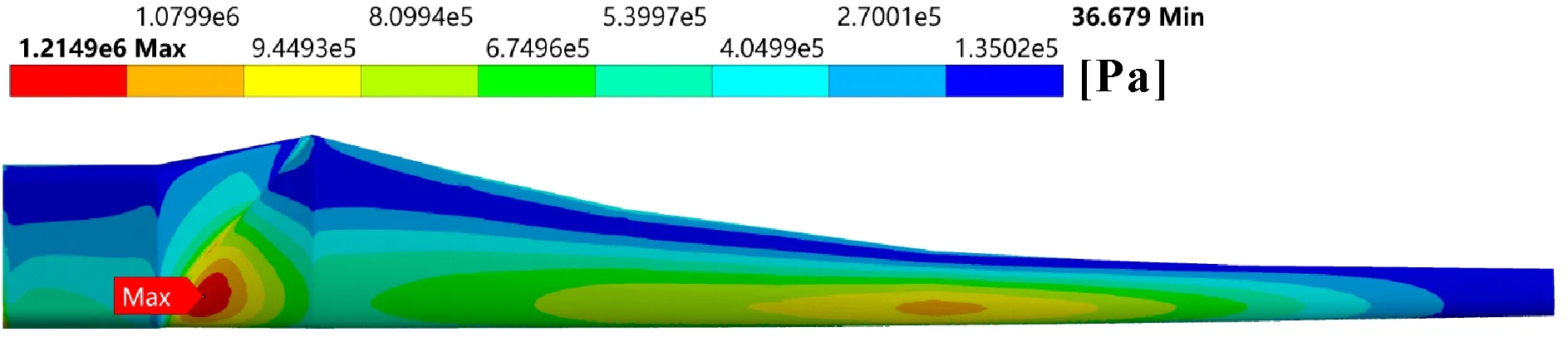
图12 冲蚀程度为1 mm×1 mm的环氧树脂材质叶片应力分布云图

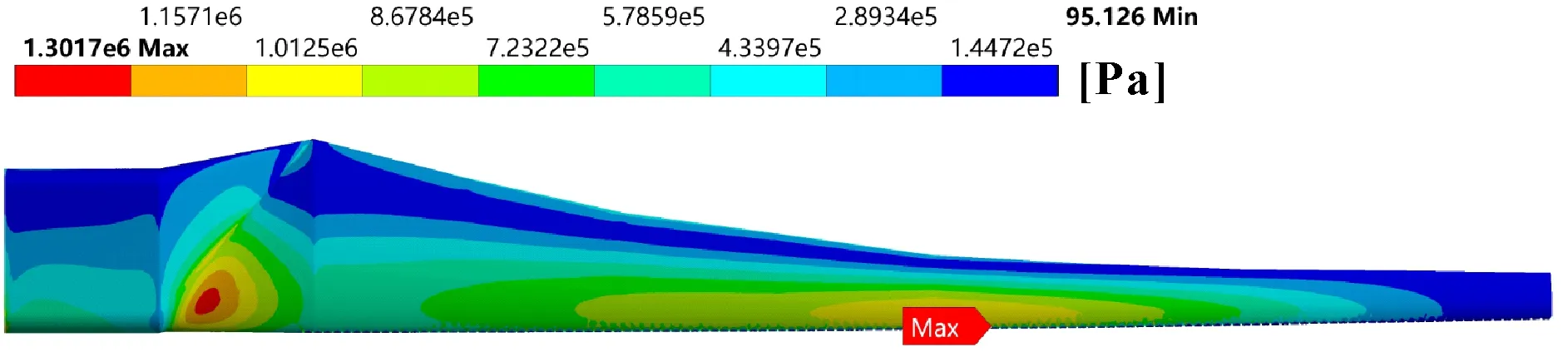
图13 冲蚀程度为3 mm×3 mm的环氧树脂材质叶片应力分布云图

以樟子松为材料同环氧树脂为材料的叶片一样，在不同载荷下，冲蚀受损处应力最大值均在冲蚀程度为3 mm×3 mm时出现。

对比图13与图14可知，当冲蚀程度从3 mm×3 mm扩大到4 mm×4 mm时，叶片的应力逐渐增大，最大值由1.302×106Pa增加到1.534×106Pa，均集中在叶片前缘受损处。

图15、图16分别为工况1下，材质为樟子松、环氧树脂叶片沿叶展方向的应力分布曲线；图17、图18分别为工况2下，樟子松叶片、环氧树脂叶片沿叶展方向的应力分布曲线；图19、图20分别为工况3下，樟子松叶片、环氧树脂叶片沿叶展方向的应力分布曲线。

图15 樟子松材质的叶片沿叶展方向的应力变化(工况1)

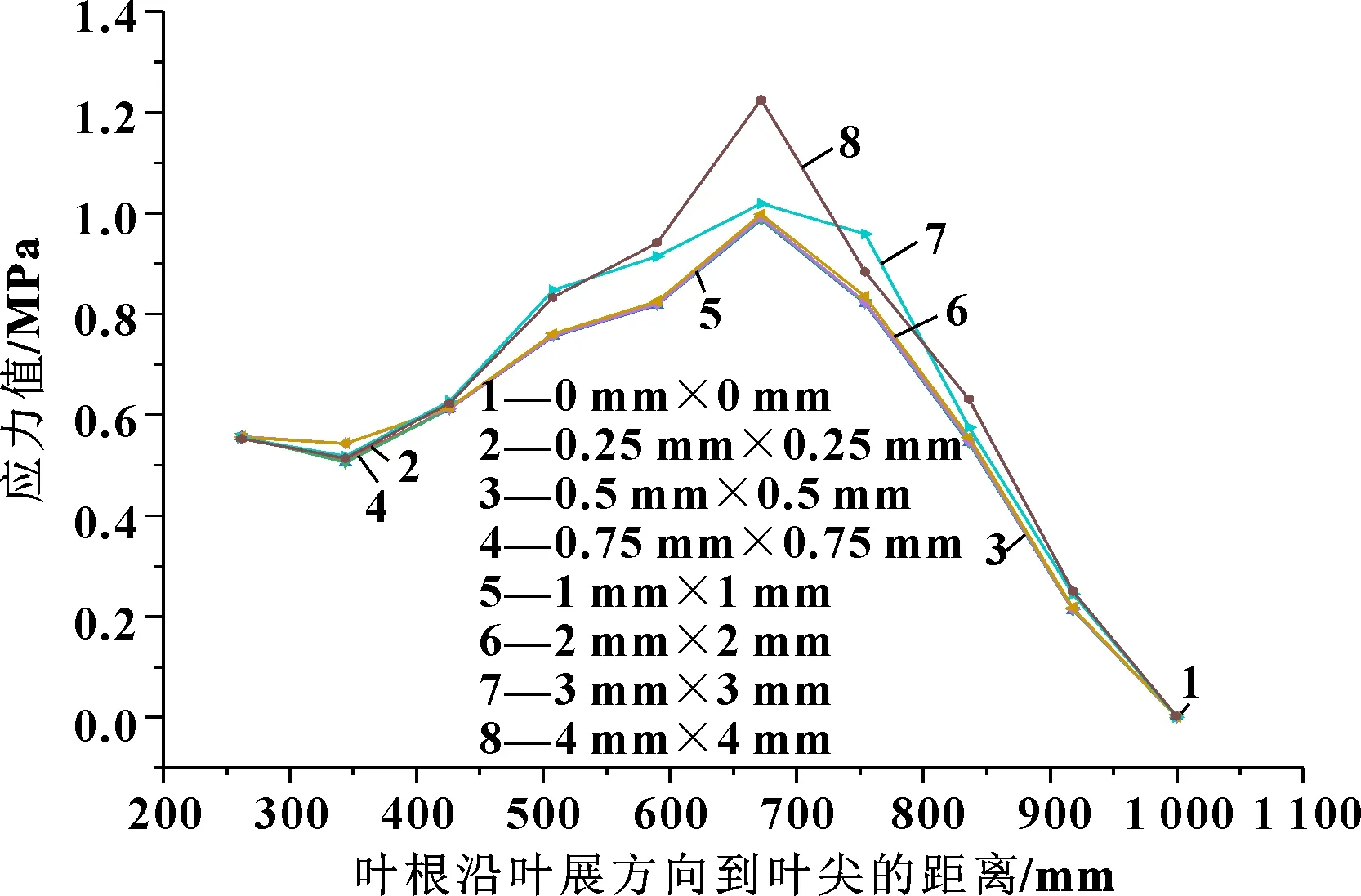
图16 环氧树脂材质的叶片沿叶展方向的应力变化(工况1)

图17 樟子松材质的叶片沿叶展方向的应力变化(工况2)

图18 环氧树脂材质的叶片沿叶展方向的应力变化(工况2)

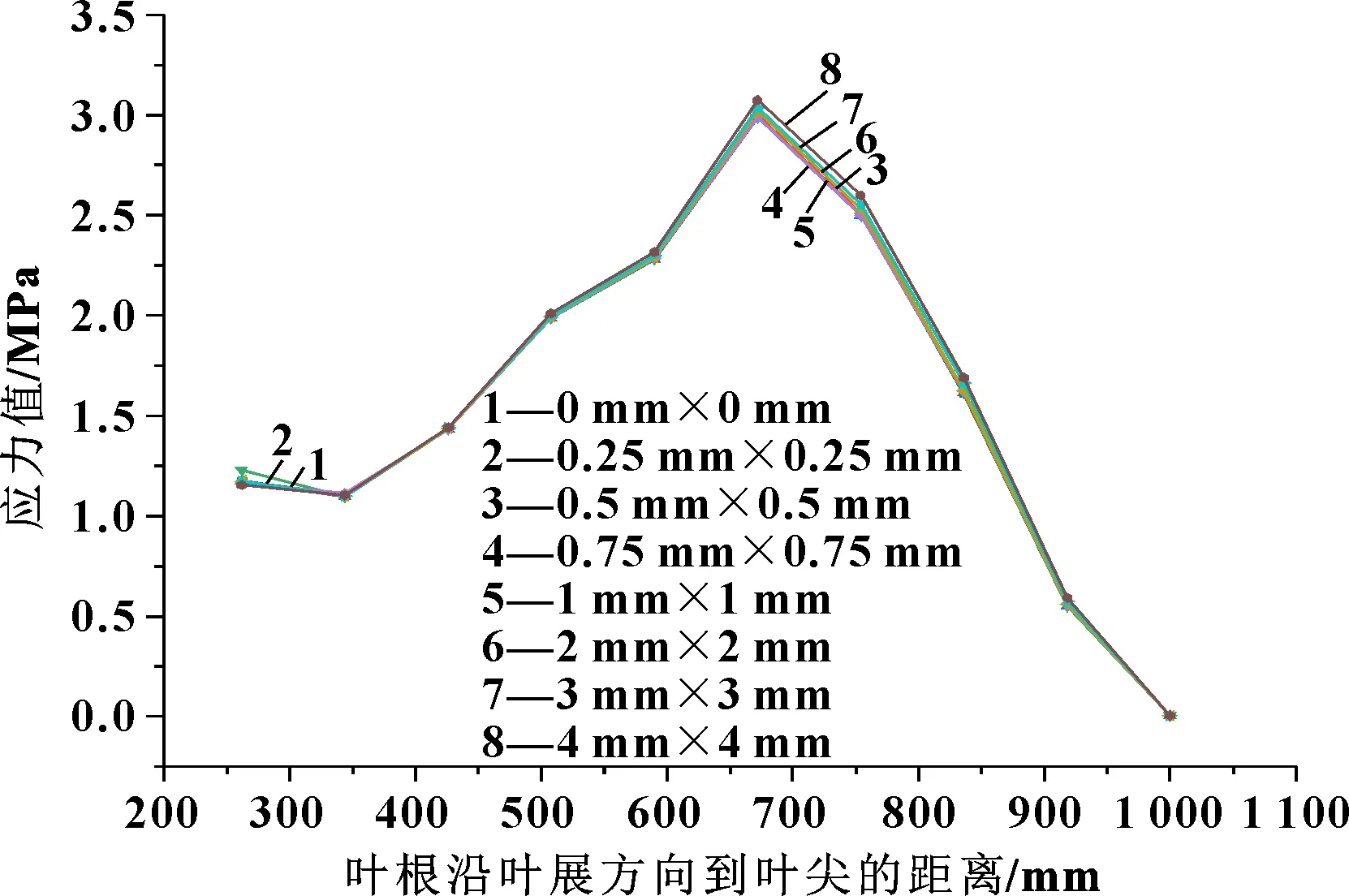
图19 樟子松材质的叶片沿叶展方向的应力变化(工况3)

图20 环氧树脂材质的叶片沿叶展方向的应力变化(工况3)

对比图15与图16发现：工况1下，不同材料的叶片应力值均在600～700 mm之间达到最大，随后逐渐减小，樟子松材质的叶片整体应力随着冲蚀程度增大，变化趋势较小；而环氧树脂叶片的磨损程度为3 mm×3 mm至4 mm×4 mm时，整体变化趋势已经发生改变。

对比图15与图17、图16与图18可以看出：当风速不变而转速增大时，两种材料叶片的应力的变化趋势浮动较大，尤其是环氧树脂，当冲蚀程度为0 mm×0 mm至2 mm×2 mm时，变化趋势相同但整体应力增大；当冲蚀程度为3 mm×3 mm时，应力在500～750 mm之间变化趋势较为平稳，4 mm×4 mm时应力变化最为剧烈，在前缘受损处达到最大值。

对比图15与图19、图16与图20可以得到：当风速、转速都增大时，两种材料下的叶片应力的变化趋势较为平稳，仅在应力值上有较大的增长；但环氧树脂材料的叶片在冲蚀程度为3 mm×3 mm时的应力曲线有较大的变化。

3.2 位移分析

图21、图22、图23分别为樟子松叶片在工况1下、不同冲蚀程度时的总位移云图，可以看出不同冲蚀程度对叶片总位移影响不大。

图21 0 mm×0 mm至1 mm×1 mm樟子松叶片总位移(工况1)

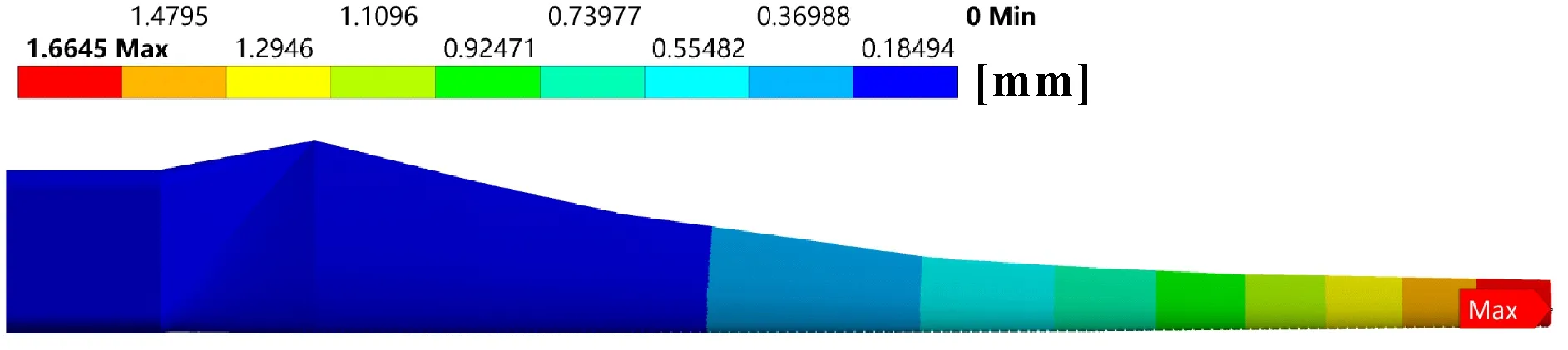
图22 3 mm×3 mm樟子松叶片总位移(工况1)

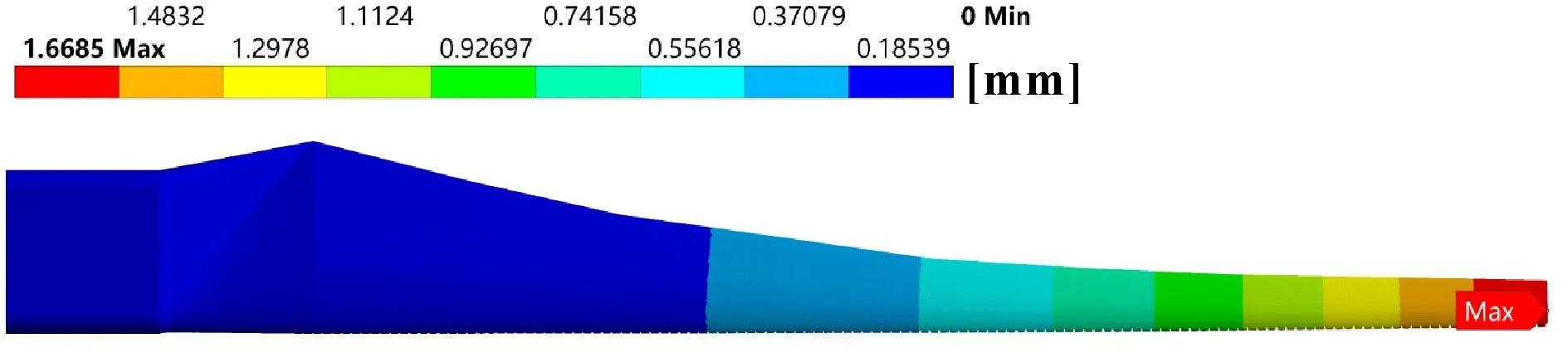
图23 4 mm×4 mm樟子松叶片总位移(工况1)

图24为樟子松叶片、环氧树脂叶片在工况1、2、3下沿叶展方向的总位移曲线，由于冲蚀程度对叶片位移影响较小，故在相同载荷下冲蚀程度选0 mm×0 mm至4 mm×4 mm位移的平均值进行比较。

图24 总位移曲线(冲蚀程度0 mm×0 mm至4 mm×4 mm)

由图24可知：叶片位移量最大值均在叶尖，不同的冲蚀程度对叶片位移影响不大；提高转速时，叶片总位移变化较小；提高风速时，叶片总位移量增加较大;当材料密度增大时，叶片总位移量增加较大。

3.3 模态分析

此节主要对工况1下两种叶片不同冲蚀程度进行研究。

图25为叶片模型的前10阶振型。叶片1阶振型主要表现为挥舞，2阶振型主要表现为摆振，3阶振型主要表现为挥舞和扭振，之后的振型主要表现为摆振、挥舞和扭振，与未受损伤的叶片振型相比变化不大。

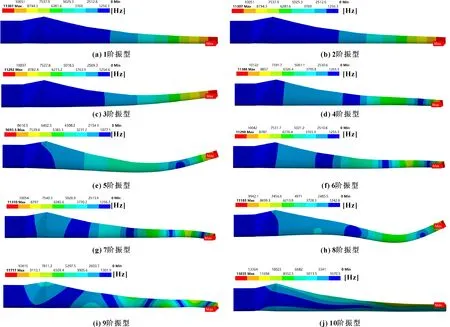
图25 叶片振型(工况1)

图26为樟子松叶片和环氧树脂叶片在工况1下不同冲蚀程度的固有频率对比曲线。

图26 固有频率对比曲线(工况1)

可见：随着材料密度增大，模态频率整体减小。变化主要集中在8阶固有频率上，随着冲蚀程度增大，固有频率随之减小。但是能量主要集中在前3阶振动上，所以不同冲蚀程度对叶片的影响极小。

4 结论

本文作者利用有限元方法对1.5 MW风力机相似模型叶片前缘磨蚀载荷进行了研究，通过对比不同载荷、不同冲蚀程度下叶片的应力、位移、固有频率，得出以下结论：

(1)冲蚀程度在0 mm×0 mm至1 mm×1 mm之间时，冲蚀深度和厚度对叶片的应力变化趋势影响较小；当叶片的材料密度越大、转速越高，对叶片的应力变化趋势影响较大，前缘受损处更容易出现应力集中；提高风速虽然会使气动载荷增大，整体应力值增大，但是整体应力的趋势变化不大。

(2)冲蚀程度增大对叶片位移影响不大，提高风速或者提高转速会使叶尖最大位移值增大，同时材料密度大的叶片位移量更大。

(3)在模态分析中，叶片的前3阶模态分析中，冲蚀程度对叶片影响极小；在第8阶模态中，随着冲蚀程度的增大，叶片的固有频率逐渐减小。