采棉头液压系统负载前馈-反馈恒速控制

刘中日，木合塔尔·克力木

(新疆大学机械工程学院，新疆乌鲁木齐 830047)

0 前言

我国是世界上棉花产量第二大国，但我国采棉机械化程度不高，棉花种植成本很高。针对我国机采棉现状，对作者所在学校研发的一种适用于中小型农户的牵引式采棉机的采棉头液压系统进行分析[1]。通过田间试验发现采棉机的采棉率未达到性能要求，经分析发现这主要是采棉头马达在负载波动下转速不稳定造成的。针对这一现象，研究阀控马达液压系统的恒速控制方法。

针对上述问题，毛雨露[2]采用基于参数自整定的模糊自适应PID控制策略,有效提高了系统的响应速度和抗干扰能力。JIANG和LIU[3]提出了一种基于模糊神经网络控制马达速度的智能控制方法，有效提高了系统的自适应能力和鲁棒性。党兵兵等[4]以机械手为研究对象，采用模糊PID控制方法,提高了动态响应能力和跟踪特性。李思升等[5]建立仿真模型，采用变结构抗饱和PI控制和模糊PID控制提高系统的控制性能。王存堂等[6]针对阀控叶片气马达转速控制问题，建立其数学模型并采用PID控制算法，提高了恒转速控制精度。闫九祥等[7]针对阀控双马达同步问题提出了双通道等同式交叉耦合同步控制策略并结合PID控制矫正提高了响应速度和稳定精度。沈伟和崔霞[8]针对马达干扰力矩会造成阀控马达速度伺服系统的速率波动问题，采用自抗扰控制器提高系统的控制效果。闫政[9]对比分析PID控制和极点配置法在阀控马达系统中的应用效果以及状态观测器极点位置对系统动态特性的影响。雷晓顺等[10]针对电液比例阀控液压马达系统,分别采用PID和参数自整定的模糊PID控制策略实现液压马达的恒速控制，仿真结果表明模糊PID的控制效果更优。孟凡虎等[11]针对阀控马达调速系统采用神经元PID改进控制算法提高了系统抗干扰能力和跟随性能。由以上分析可知，针对阀控马达速度控制系统，多是采用PID或其改进控制算法改善控制效果。本文作者针对比例阀控马达系统，根据系统数学模型设计二阶自抗扰控制器，对整个系统的扰动进行观测并进行补偿，改善系统的动态响应，再针对负载扰动设计前馈控制器补偿稳态误差，为这种复合控制方法在阀控马达系统中的应用提供参考。

1 系统建模

1.1 比例方向阀传递函数

比例电磁铁线圈的电流与输出电压的方程为

(1)

式中:L为线圈动态电感；R为线圈内阻。

工作在线型区的比例电磁铁的输出力为

FM(t)=Kii(t)

(2)

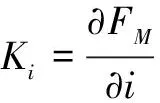
阀芯位移的微分方程为

(3)

式中：FM为电磁铁输出力;m为阀芯质量；xv为阀芯位移；c为阀芯动态阻尼系数；ks为衔铁组件的弹簧刚度。

由上式(1)(2)和(3)推导出阀芯位移与误差电压的传递函数为

(4)

式中：Kux为输入电压-阀芯位移增益。

1.2 阀控马达传递函数

三位四通比例阀流量方程为

qL=Kqxv-KcpL

(5)

式中：qL为比例阀的输出流量；pL为负载压力；Kq为流量增益；Kc为流量-压力系数。

液压马达的流量连续性方程为

(6)

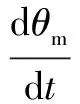
马达与负载的力矩平衡方程为

(7)

式中：Jm为液压马达和负载折算到马达轴上总惯性;T为作用在马达轴上的任意外负载力矩；Bm为液压马达和负载的黏性阻尼系数；G为负载扭转弹簧刚度。

联立方程式(5)(6)和(7)，消去中间变量，可得到以马达转角为输出、以阀芯位移和外负载力矩为输入的方程式为

θm=

(8)

式中：Kce为总流量-压力系数。

考虑到马达与负载之间是刚性连接，并且黏性阻尼系数也很小，可以将式(8)简化为

(9)

(10)

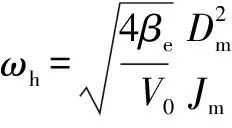
2 控制器设计

2.1 自抗扰控制器设计

自抗扰控制器(Active Disturbance Rejection Control,ADRC)[12]是由PID控制器演变而来，不依赖于系统的精确模型，包含TD微分跟踪器、扩张观测器和状态误差反馈控制律3个部分。本文作者设计的非线性自抗扰控制器框图如图1所示。在自抗扰控制器中，扩张观测器可以观测到系统的总误差(包括内扰动与外扰动)，然后给出控制量进行补偿。因此合理地设计扩张状态观测器的阶次较为重要，适当地降低系统阶次可以简化控制器的结构，降低控制器的调节难度，提高实用价值[13]。

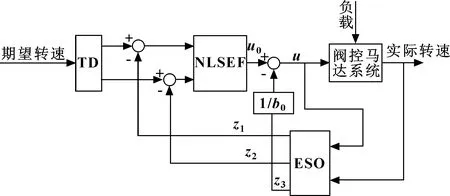
图1 非线性自抗扰控制器框图

由数学模型可知，阀控马达系统由两个二阶振荡环节串联而成。一般来说，阀控马达环节的动态响应最低，远低于比例阀环节，可以将比例方向阀的动态响应看成比例环节，从而可以将系统简化为一个二阶振荡环节。因此选择阶次2是较为合适的。

令x1=ωm,根据数学模型建立系统状态空间方程：

(11)

则状态扩张观测器为

(12)

fal函数表达式为

(13)

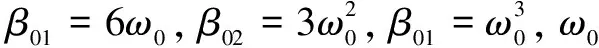
2.2 误差补偿控制率

ADRC控制率可以看成PD控制，通过对TD跟踪器得出的信号及其微分与观测器得到的系统输出及其导数的误差用非线性函数fal处理，再对其加权组合来实现控制和扰动补偿。

u0=kpfal(v1-z1,α1,TS)+kdfal(v2-z2,α2,TS)

(14)

(15)

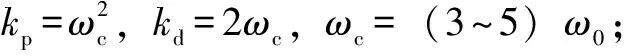
2.3 前馈控制器的设计

负载前馈控制就是在调节系统的过程中直接测量外界负载的变化，当扰动出现时可以通过前馈控制器将负载扰动量转化为电信号补偿量，动态补偿系统误差。负载前馈+ADRC转速控制方法原理如图2所示。

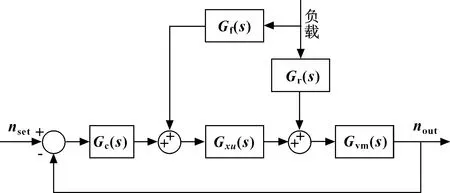
图2 负载前馈-自抗扰反馈控制原理

图2中：Gc(s)为含有自抗扰的系统反馈传递函数；Gr(s)为负载干扰的输入信号传递函数；Gxu(s)为比例控制阀的传递函数；Gvm(s)为系统阀控马达环节的传递函数；Gf(s)为负载前馈传递函数。通过前馈+自抗扰复合控制框图求得输出转速传递函数为

nout=nset[Gc(s)Gvm(s)[Gxu(s)Gf(s)+Gr(s)]]

(16)

比例阀控马达系统在自抗扰反馈控制下，马达的转速会逐渐达到稳态，利用前馈控制对由负载干扰引起的转速波动进行补偿，使系统响应的静态偏差趋于零，可以得到前馈控制器的传递函数为

(17)

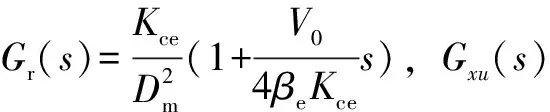
3 仿真结果分析

利用MATLAB/Simulink工具搭建系统框图，对比例阀控马达系统进行恒速控制仿真，分别研究PID、ADRC、负载前馈+ADRC三种控制方式下，马达转速阶跃响应以及在突变负载作用下马达转速的动态响应。仿真中，数学模型参数设置如表1所示。

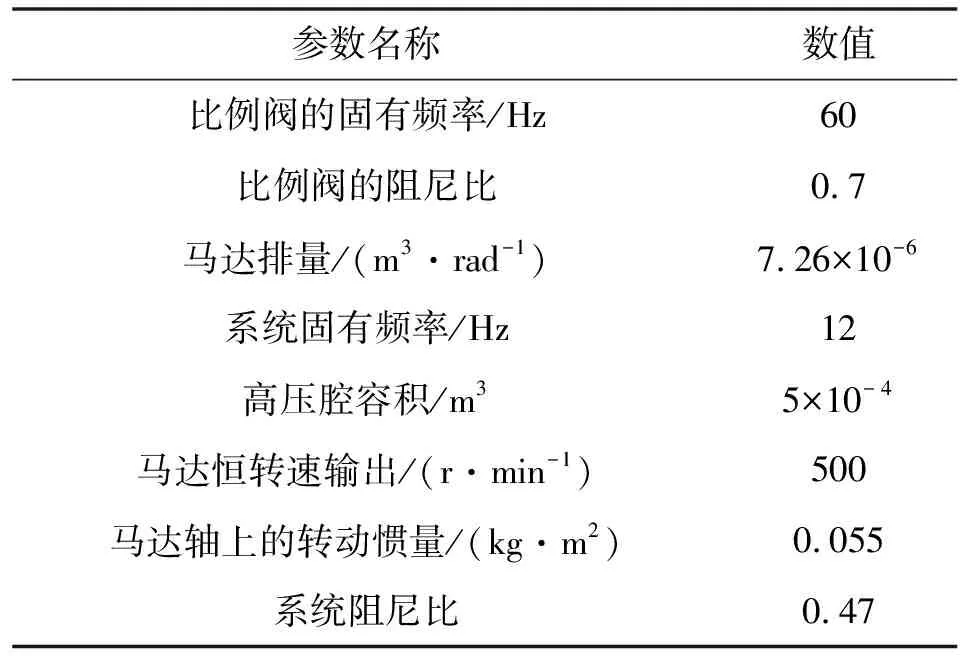
表1 数学模型参数

自抗扰控制器参数设置为：微分跟踪器中h=0.002，r=20 000；状态扩张观测器中δ=0.005，b0=100 000，β01=20，β02=5 000，β03=100 000；反馈控制率中α1=0.5，α2=0.6，kp=500，kd=7，Ts=0.01。

仿真过程中，首先对比分析采用PID、自抗扰控制以及复合控制方法下系统受恒负载时的阶跃响应特性，然后对比分析3种控制策略下系统受到波动负载时的转速响应曲线。响应曲线如图3所示。

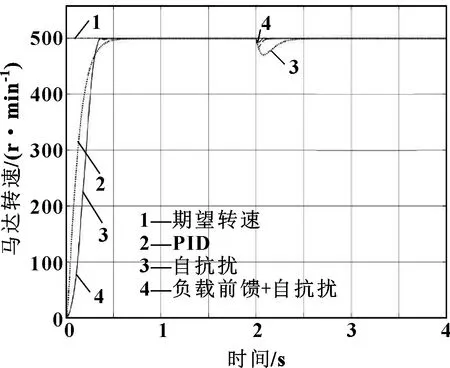
图3 突变负载下转速响应曲线

由仿真结果可知：当输入阶跃信号时，马达的转速经过调整后都达到稳态，基本无稳态误差，且未出现超调。PID控制下阶跃响应时间为0.8 s；自抗扰控制下，响应时间为0.5 s，阶跃响应时间减小了37.5%；而复合控制下系统阶跃响应曲线与自抗扰控制下一致。

在t=2 s时输入突变负载时，马达转速出现波动，然后再达到稳态值，基本稳定在期望转速附近。仿真结果如图3所示，PID、ADRC以及复合控制时，超调量分别为5.92%、3.2%、1.6%，稳定调节时间分别为0.62、0.3、0.28 s。采用自抗扰控制方法的系统输出转速相较于PID控制超调量减小45.9%并且调节时间减少53.3%；负载前馈+自抗扰复合控制相比于自抗扰控制，在稳定时间方面基本没有减少，而超调降低了50%，验证了负载前馈控制器有效补偿了负载波动引起的转速波动问题。具体结果对比如表2所示。

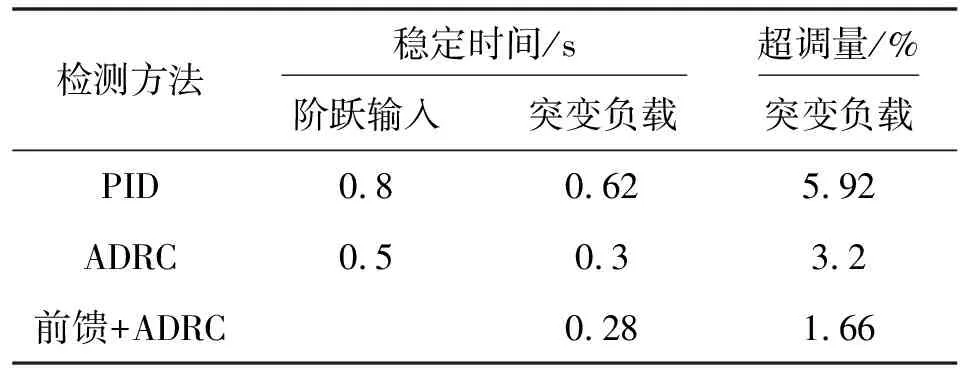
表2 系统输出结果对比

考虑到采棉机实际采棉过程中，采棉头部分所受负载会一直波动，因此在仿真过程中t=2 s位置输入一个正弦波函数f(x)=200+100 sin10x模拟负载变化，得到的响应曲线如图4所示。前馈+自抗扰复合控制下，马达转速会下降到488.5 r/min，经过0.41 s恢复稳定状态且没有稳态误差；PID控制下，马达转速会下降到460 r/min，然后会在期望转速±13.8 r/min左右周期性波动，不能稳定。

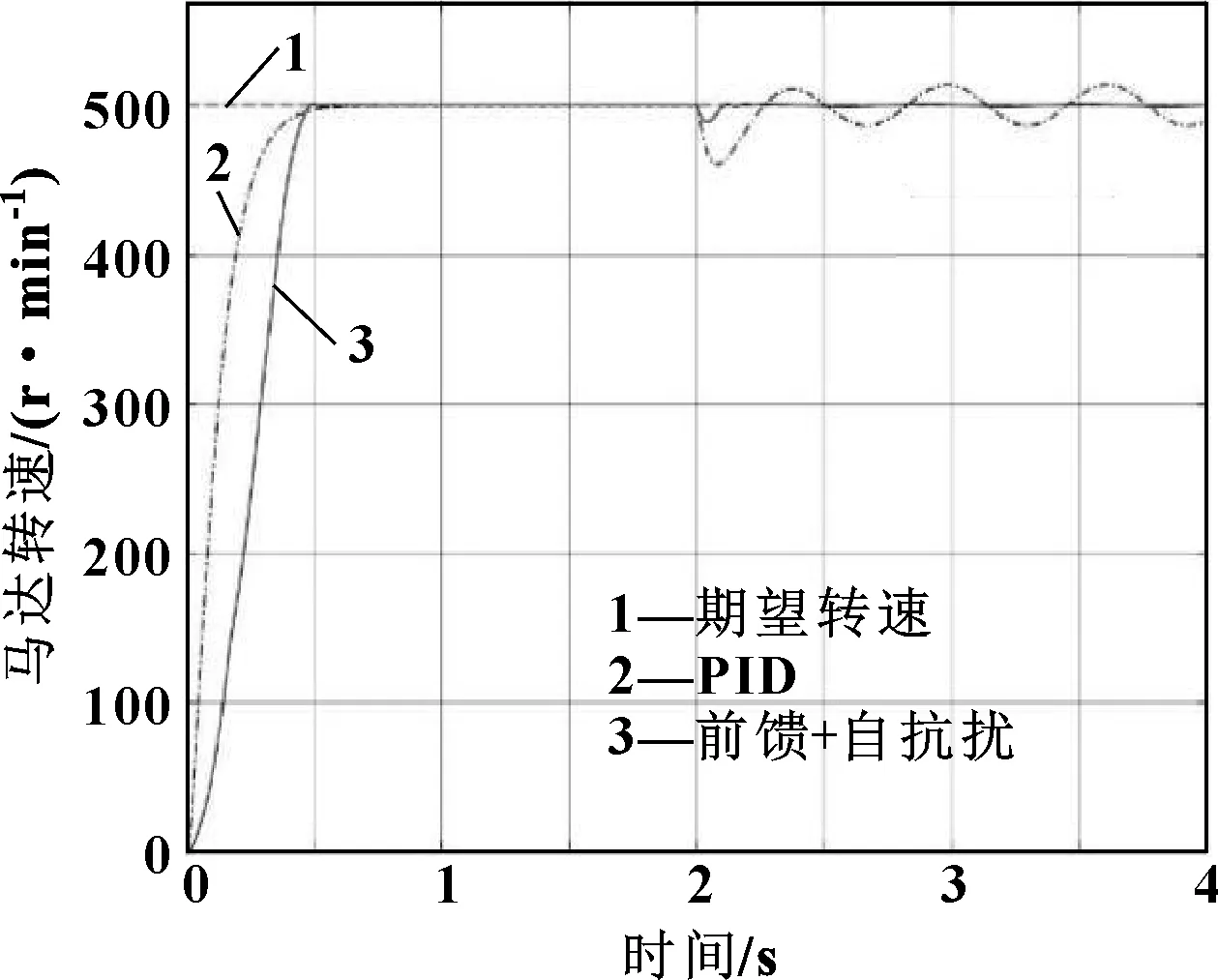
图4 周期变化负载下转速响应曲线

4 结论

针对比例阀控马达速度伺服系统中存在的外部扰动、模型参数不确定等问题,设计了前馈补偿与自抗干扰控制结合的复合控制器，并对其进行仿真分析,得出以下结论。

(1)针对比例阀控马达系统阶跃输入以及突变负载干扰下恒转速输出问题，提出了一种基于负载前馈补偿+ADRC转速控制方法，有效抑制了马达转速的波动问题，提高了系统的动态性能。

(2)相比于传统PID控制方法，负载前馈+自抗扰复合控制方法有效提高系统的稳定性和鲁棒性。通过仿真得出：恒负载阶跃输入时，系统的响应时间减少了23.3%;在突变负载作用下，马达输出转速的最大超调量下降了66.7%，稳定时间减小了59.6%。特别在负载变化的情况下，复合控制具有更好的抗干扰能力以及稳定性能。