弧齿锥齿轮齿面数学建模方法

田国富，赵继宁

(沈阳工业大学机械工程学院，辽宁沈阳 110870)

0 前言

弧齿锥齿轮正朝着高速、重载和轻量化的方向发展。长期以来，可用于螺旋锥齿轮的齿面类型受到限制，并且型号很少。齿轮齿面的形状取决于所用机床刀具的形状，严重影响了工业设备的进一步发展应用[1]。

目前可查到的文献，主要通过分析齿面的几何设计、加工制造及接触，实现齿面优化，提高齿面的承载能力。但尚未查到关于提高齿轮传动性能的研究。

弧齿锥齿轮的啮合过程和齿面形状极为复杂，因此其建模过程异常困难。该方法和一般齿轮的共轭曲面成形理论不同，它以齿轮的啮合理论为基础，运用MATLAB 作为运算辅助工具，利用三维软件SolidWorks进行三维绘制，以研究一种快速精确的齿轮齿面设计方法。该方法的研究有利于推进弧齿锥齿轮制造工艺的发展和进行齿轮有限元分析[2]。

1 齿面成形机制

1.1 齿轮的啮合方程

2个齿轮相互啮合传动的基本要求是齿轮2个相互接触的齿面必须相切于空间的某一点，如图1所示。分别设置S1和S2为齿轮相互啮合的2个齿面，且相切于点M，无论2个齿面如何运动，点M都在2个运动曲面上。这2个齿面S1和S2上分别有坐标系σ1和σ2，并随着齿面的运动而运动。

图1 啮合曲面相切于点M

在曲面S1和S2上分别设置径向矢量r1和r2、法向矢量n1和n2，设置O1和O2分别为坐标系σ1和σ2的原点，则由O1到O2径向矢量m=O1O2[3]。根据齿轮的啮合原理，切点M处的2个曲面必须满足接触并且相切的要求，则有如下方程组：

(1)

当齿轮的2个接触齿面在点M处接触时，条件是上述方程组中的第1个公式；当2个齿面在点M处相切时，条件是上述方程组中的第2个公式[4]。齿轮在旋转过程中要达到啮合状态，必须满足方程组(1)。采用相对微分的方法，对接触点的曲率、速度进行转换，在齿面啮合接触的位置，还需要满足以下条件：

v12·n=0

(2)

该方程的物理含义：2个运动表面的法向子速度必须相等，以确保2个运动表面连续啮合。否则，这2个表面将在下一刻分离或彼此嵌入，但这是不被允许的[5-6]。

在弧齿锥齿轮2个相互接触啮合的齿面，无论是线接触还是点接触均应同时满足公式(1)和公式(2)[7]。

1.2 齿轮加工坐标系的建立

根据螺旋锥齿轮的啮合运动关系建立坐标系，创建机床坐标系Sm、摇台坐标系Sg、刀盘坐标系St、辅助坐标系Sn和Sq、工件坐标系S1,这些坐标系的空间位置关系如图2所示[8]。

图2 弧齿锥齿轮铣齿加工坐标系

1.3 大轮齿面方程的建立

图3所示为刀具切削锥面。大轮刀具的切削面(锥面)方程rt和法线方程nt在坐标系Ot中表示。

图3 刀具切削锥面

(3)

(4)

其中：“-、+”由加工齿轮的凹凸面决定，凹面为“-”、凸面为“+”[9-10]。

经过坐标变换，大轮切削面方程为

r2(up,θp,φp)=M2a·Mam·Mmp·Mpe·re

(5)

式中：M2a、Mam、Mmp、Mpe为坐标变换矩阵。为方便计算，可以消去一个参数up，因此，在固定坐标系Sm中建立啮合方程：

vm·nm=0

(6)

求解式(5)、(6)，则可以消除参数up，得到大轮齿面方程r(θp,φp)。

2 齿面点获取

选择一组成对的弧齿锥齿轮，具体参数如表1所示，并以此齿轮为例获取齿面点。

表1 齿轮基本参数

通过齿面方程得到的曲面是一种空间复杂曲面，对于整个齿轮，齿面只是整个曲面的一部分。因此，有必要确定齿面变量的范围[11-12]。

旋转曲面并将它投影到其轴向滑动平面上，再对轴向滑动平面上的投影面进行网格划分，如图4所示。

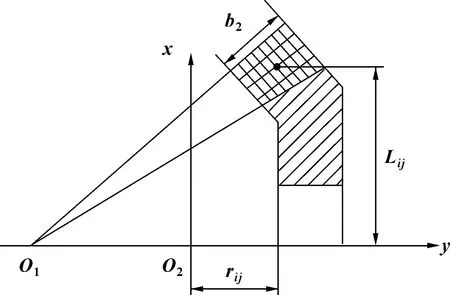
图4 齿面旋转坐标

将投影平面离散化以获得一组用于齿侧面的三维坐标方程，即轴截面上的投影齿侧面点的坐标值；建立齿面与轴截面点之间的对应函数关系；根据函数得到齿面离散点的坐标[13]。获取齿面点的具体流程如图5所示。

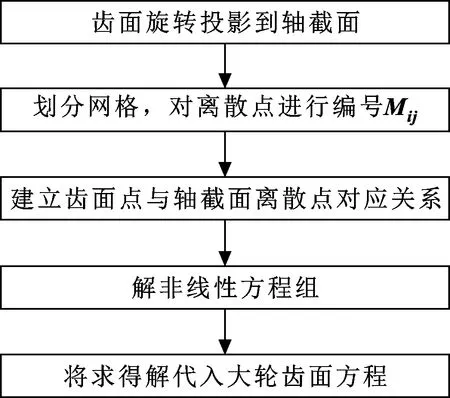
图5 求大轮离散点坐标流程

根据以上理论公式和流程，编写MATLAB程序，求出齿轮基本参数、齿面方程，输出一个齿轮凸面，具有5×9=45个数据点，得到这些点在大轮凸面上的离散坐标值[14-15]。表2为部分齿面点三维坐标。

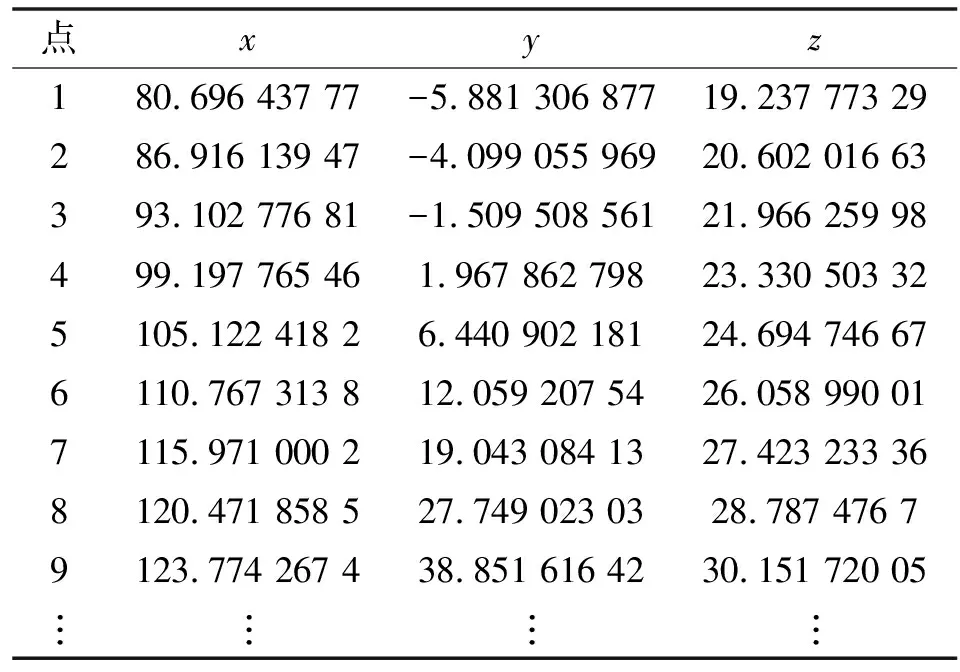
表2 大轮部分齿面点坐标

3 齿面成形

文中使用MATLAB作为计算工具获取的齿面点，求解齿轮的齿面方程和齿面点的坐标值，并计算其3D坐标值。通过编制的程序导出齿面离散点的坐标，并以SolidWorks可识别的文件格式保存[16-17]。该程序的一部分如下所示：

disp(′*齿面方程计算点*′)

pp(9,1)=Xe2;

pp(9,2)=de2/2;

pp(45,1)=Xe2+(ht-c)*sin(a2);

pp(45,2)=de2/2-(ht-c)*cos(a2);

l1=b/cos(Qa2);

l2=b/cos(Qf2);

kk1=tan(aa2);

kk2=tan(af2);

pp(37,1)=pp(45,1)-l2/sqrt(1+kk2^2);

pp(37,2)=pp(45,2)-kk2*pp(45,1)+kk2*pp(37,1);

pp(1,1)=pp(9,1)-l1/sqrt(1+kk1^2);

pp(1,2)=pp(9,2)-kk1*pp(9,1)+kk1*pp(1,1);

ll{1}=linspace(pp(1,2),pp(37,2),5);

ll{9}=linspace(pp(9,2),pp(45,2),5);

rrr{1}=linspace(pp(1,1),pp(37,1),5);

rrr{9}=linspace(pp(9,1),pp(45,1),5);

将通过MATLAB获得的45个齿面点分成5组，并分别保存为.txt格式，导入到SolidWorks中以形成大轮凸面曲线，如图6所示。

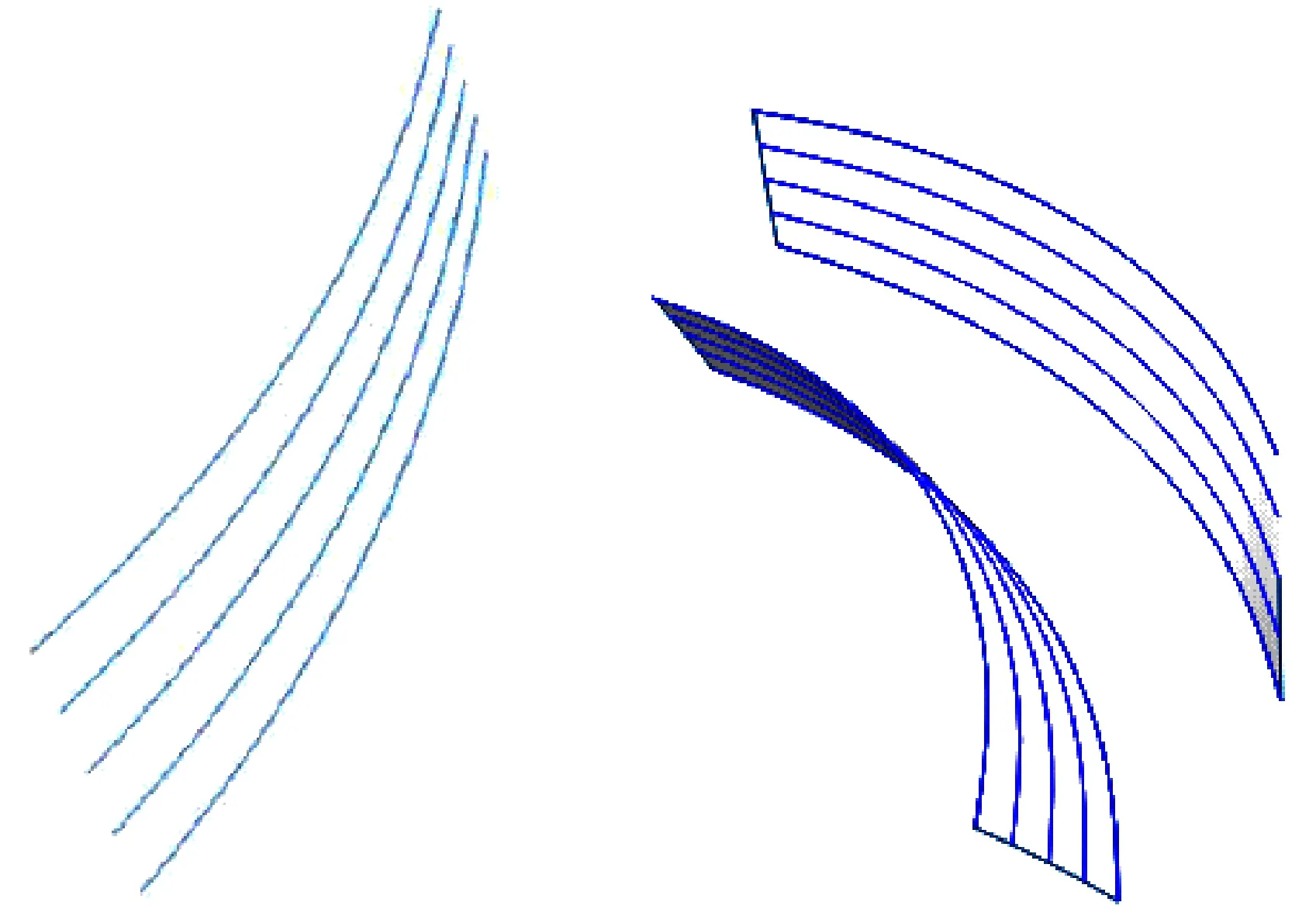
图6 大轮凸面曲线 图7 大轮凹凸面

再将曲线通过放样曲面、缝合、延伸命令生成凸面，用同样的方法生成齿面凹面并将它导入SolidWorks中，如图7所示。根据螺旋锥齿轮轮坯的设计标准，确定齿轮轮坯的基本参数和修改参数，完成轮坯的设计。将凹凸面进行放样切割，得到如图8所示的齿槽，然后再进行环形阵列，得到如图9所示的齿轮，至此完成弧齿锥齿轮大轮的精确建模。

图8 大轮齿槽 图9 大轮模型

4 总结

螺旋锥齿轮的齿面非常复杂，而3D模型构建的准确性直接影响后续性能分析的准确性。本文作者研究了一种高速精确建模方法，以齿轮啮合原理为理论基础，MATLAB作为运算工具，提高了齿轮齿面的精度，为弧齿锥齿轮的加工提供参考，也可以为圆弧齿廓齿面的研究提供模型参照。在获得完整齿廓表面模型的基础上，可以提高齿轮寿命和传动效率，为研究和讨论各种应用技术提供参考。