正常使用极限状态下CRTS Ⅱ型轨道板体系可靠度分析

张玄一，王基全,卢朝辉，赵衍刚

(1.山东铁路投资控股集团有限公司，山东 济南 250102；2.北京工业大学 城市与工程安全减灾教育部重点实验室，北京 100124)

作为我国综合交通运输体系的骨干，高速铁路对我国经济社会发展具有至关重要的作用，如何确保高速铁路长期安全稳定运营是我国现阶段面临的突出问题[1]。高速铁路CRTS Ⅱ型板式无砟轨道广泛应用于我国京沪高速铁路、京津城际铁路，该轨道结构为竖向多层、纵向连续的带状结构，自上而下分别为钢轨、扣件、轨道板、乳化沥青水泥砂浆和支承层。其中，CRTS Ⅱ型轨道板起承载和固定钢轨位置的作用，一旦失效将严重影响高速铁路的正常运输效率，甚至危及高速列车的运行安全。在列车荷载和温度共同作用下，CRTS Ⅱ型轨道板存在多种可能的失效模式，包括对应承载能力极限状态的安全性失效模式和对应正常使用极限状态的适用性失效模式。我国高速铁路运营实践表明，CRTS Ⅱ型轨道板的安全性失效模式鲜少出现，但已经出现了翘曲、开裂等性能劣化现象。随着劣化的进一步开展，CRTS Ⅱ型轨道板可能发生适用性失效，即CRTS Ⅱ型轨道板在正常使用极限状态下的可靠度难以保证。因此，为确保高速列车的安全高效运营，有必要开展CRTS Ⅱ型轨道板在正常使用极限状态下的可靠度分析。

正常使用极限状态下，CRTS Ⅱ型轨道板存在纵向裂缝宽度过大、横向开裂以及翘曲变形三种失效模式。张国虎[2]探讨了轨道板裂缝宽度过大这一失效模式的可靠度，并基于可靠度分析结果开展了轨道板耐久性评估。李怀龙等[3]通过假设列车荷载和温度梯度荷载的概率分布，对轨道板轨下截面和轨中截面的横向开裂失效模式可靠度进行研究。赵磊等[4]研究了列车荷载作用下轨道板横向开裂失效模式下的可靠度，并探讨了不同因素对轨道板可靠度的影响程度。欧祖敏[5]考虑大气环境碳化作用、寒冷地区冻融环境冻融循环作用的影响，开展了轨道板多种疲劳失效模式下的可靠度分析。邹红等[6]考虑抗力衰减效应开展了轨道板横向抗裂的时变可靠度研究，探讨了轨道板不同位置处的可靠度变化规律。可见，目前围绕CRTS Ⅱ型轨道板纵向裂缝宽度过大和横向开裂可靠度，已经取得了部分研究成果，但现有研究尚未考虑CRTS Ⅱ型轨道板在翘曲失效模式下的可靠度，更未综合考虑所有重要适用性失效模式开展正常使用极限状态下的体系可靠度分析。由于各适用性失效模式的极限状态函数间存在共同随机变量，适用性失效模式间具有一定的相关性，而单独考虑各适用性失效模式开展CRTS Ⅱ型轨道板可靠度分析相当于人为假定各失效模式间相互独立，与实际情况不符，将带来一定的误差。

本文研究CRTS Ⅱ型轨道板正常使用状态下综合考虑各适用性失效模式的体系可靠度，具体包括：首先分析CRTS Ⅱ型轨道板在列车荷载和温度作用下的结构响应；随后构建纵向裂缝宽度过大、横向开裂以及翘曲变形三个适用性失效模式的极限状态函数及正常使用极限状态下的体系极限状态函数；最后，使用高阶矩法开展CRTS Ⅱ型无砟轨道板正常使用极限状态下的体系可靠度研究，并分析了关键参数对CRTS Ⅱ体系可靠度的影响。

1 CRTS Ⅱ型轨道板主要承受的荷载作用

CRTS Ⅱ型轨道板承受的荷载作用可以归纳为列车荷载作用、温度作用以及桥梁变形作用三方面[7]。为对轨道板的可靠度进行评估，需要了解上述荷载作用下轨道板的结构响应。由于正常使用极限状态下的失效模式与桥梁变形无关，因此本章主要针对列车荷载和温度作用下的CRTS Ⅱ结构响应进行分析。

1.1 列车荷载作用

在无砟轨道运营周期内，列车荷载通过钢轨和扣件以弯矩的形式传递到轨道板上。列车荷载作用可以分解为横向列车荷载、纵向列车荷载以及竖向列车荷载三类。

(1)横向列车荷载作用下的轨道板响应

我国采用简化法对横向列车荷载Q进行分析，将其近似取为0.8倍静轮载Pj[8]。横向列车荷载作用下，轨道板上主要产生横向弯矩ML，表达式为[9]

ML=0.3Qha

( 1 )

式中：ha为轨道板至轨面的距离，本文使用CHN60轨分析，因此取ha= 176 mm。

(2)纵向列车荷载作用下的轨道板响应

在制动力的作用下，轨道板内主要产生拉应力。假定制动力经扣件完全转化为轨道板和支承层(底座板)的拉力。此时，轨道板单位长度上的制动力Fb可以近似表示为[9]

( 2 )

式中：ncj为单个钢轨单位长度上的扣件个数,ncj=10；Fcj为扣件阻力；f′c、f′d分别为轨道板和底座板混凝土抗拉强度,f′c=2.74 MPa,f′d=2.01 MPa；Ag、Ad分别为轨道板、底座板的截面面积,Ag= 0.51 m2，Ad=0.59 m2。

(3)竖向列车荷载作用下的轨道板响应

竖向列车荷载作用下，轨道板内将产生纵向弯矩Mfl及横向弯矩Mfh。由于CRTS Ⅱ型板式无砟轨道结构体系层间作用机制复杂，使用解析方法求解Mfl和Mfh较为困难。因此，本文采用有限元法对竖向列车荷载作用下的CRTS Ⅱ型无砟轨道板结构响应进行分析。由于弹性地基梁-板模型能够较好模拟结构体系的变形，且计算效率相对较高，因此本文采用弹性地基梁-板模型对CRTS Ⅱ型板式无砟轨道结构体系进行模拟，如图1所示。各结构层次采用的单元以及参数见表1。

图1 CRTS Ⅱ型无砟轨道有限元模型

表1 CRTS Ⅱ型板式无砟轨道结构体系有限元模型计算参数

为验证有限元模型的正确性，使用本文有限元模型对竖向列车荷载取为三倍列车静轮载的情况进行分析，得到的结构体系纵横向弯矩应力分布如图2所示，其中轨道板的纵横向弯矩最大值分别为14.202、12.578 kN·m，该结果与现有研究成果[10]一致，可以初步判断本章所使用的有限元模型具有较高的准确度。

图2 竖向列车荷载作用下CRTS Ⅱ型无砟轨道纵横向弯矩分布(单位：N·m)

1.2 温度作用

CRTS Ⅱ型轨道板为钢筋混凝土结构，具有导热系数小、传热性差等特点。因此，温度荷载对轨道板的影响极为明显，由于温度作用而产生的应力和变形等可能导致轨道板的破坏。温度作用包含轴向温度作用(也称整体温度作用)ΔT和温度梯度作用Tg两种。同时，由于混凝土收缩徐变对轨道板产生的影响以等效温降ΔTck来近似表达，因此由于混凝土收缩徐变产生的轨道板响应也近似算作温度作用一并分析。

(1)轴向温度作用

轴向温度作用指均匀升温降温引起的结构反应。轴向温度作用主要在轨道板内部引起拉(压)应力，由轴向温度作用产生的应力标准值Ftk表示为[3]

Ftk=λcEcatΔTAg

( 3 )

式中：λc为弹性模量的折减系数，本文取为0.5；Ec为轨道极弹性模量；at为线膨胀系数。

在进行体系可靠度分析时，由于随机变量较多且材料特性变异性较荷载作用变异性相对较小，因此式( 3 )中Ec=35.5 GPa和at=10-5/℃。

(2)温度梯度作用

温度梯度作用主要指轨道板板顶和板底之间的温度差引起的结构响应。正温度梯度指的是轨道板板顶温度高于轨道板板底温度的情况，负温度梯度指的是轨道板板底温度高于轨道板板顶温度的情况。温度梯度作用下，轨道板会发生翘曲，从而在内部产生拉应力、弯矩以及翘曲应力。温度梯度产生的纵向拉力Fttk，通过使用温度梯度Tg的一半替代ΔT使用式( 3 )近似求解[10]，正温度梯度时Fttk取为负值，负温度梯度时Fttk取为正值。温度梯度作用下，轨道板内将同时产生纵向弯矩Mtl以及横向弯矩Mth，Cornell[11]建议Mtl和Mth采用威氏公式计算，表示为

( 4 )

式中：ah为温度梯度板厚修正系数，ah=1.05；h为轨道板厚度,h=200 mm。

(3)混凝土徐变作用

混凝土收缩徐变下轨道板内部主要产生拉应力。由混凝土收缩徐变引起的拉应力标准值Fck可以使用式( 3 )近似求解[9]，其中ΔT的取值为ΔTck。

2 CRTS Ⅱ型轨道板的极限状态函数

2.1 轨道板纵向抗裂极限状态函数

正常使用状态下，CRTS Ⅱ型轨道板允许在V形槽(即假缝)处纵向开裂，但裂缝的宽度需处于允许范围内。因此，在进行桥上CRTS Ⅱ型无砟轨道板结构可靠度分析时，有必要对该其纵向开裂失效模式进行考虑，并将其极限状态函数纳入体系极限状态函数中分析。根据GB 50010—2010《混凝土结构设计规范》[12]对正常使用状态下混凝土构件裂缝宽度的验算要求，轨道板最大裂缝宽度的极限状态函数G1(X)计算式为

G1(X)=1-wmax/[wmax]

( 5 )

式中：[wmax]为规范规定的裂缝宽度允许值，[wmax]=0.3 mm；wmax为轨道板在外力作用下的最大纵向裂缝宽度，计算式为[2]

( 6 )

CRTS Ⅱ型板式无砟轨道纵向在中性层上下各配有8φ8 mm的HRB500普通钢筋；中性层附近配有6φ20 mm的HRB335普通钢筋，精轧螺纹钢筋连接。因此，deq近似取为8 mm，ρte近似取为0.134。σs为荷载准永久组合(本文主要包含列车荷载和温度作用)下的钢筋混凝土构件纵向普通钢筋的应力，计算式为

( 7 )

2.2 轨道板横向抗裂极限状态函数

CRTS Ⅱ型板在正常使用过程中，除轨道板假缝处允许开裂外，其余部位不允许开裂。因此，轨道板横向抗裂极限状态为轨道板发生横向开裂。相应的极限状态函数表示为极限开裂弯矩与实际弯矩间的关系[6]

G2(X)=1-(Mfh+ML+Mth)/Mcr

( 8 )

式中：Mcr为轨道板横向开裂弯矩允许值。张国虎[2]搜集了12组轨道板开裂试验数据，基于试验数据可以得到Mcr的前四阶矩分别为均值μMcr= 52.942 kN·m，变导系数COVMcr= 0.134，偏度α3Mcr= 0.989，峰度α4Mcr= 3.637。

2.3 轨道板翘曲变形极限状态函数

轨道板在温度梯度下产生的翘曲变形有可能超过轨道板的极限翘曲变形承载力，从而造成轨道板破坏，影响高速列车行车安全。因此，有必要在对CRTS Ⅱ型轨道板结构可靠度进行考察时，考虑轨道板翘曲变形失效模式。轨道板翘曲变形失效模式对应的极限状态函数表示为翘曲应力允许值σuq与温度梯度作用下轨道板产生的翘曲应力σq间的关系为

G3(X)=1-σq/σuq

( 9 )

刘学毅等[13]通过对不同约束条件和不同砂浆层弹性模量下的轨道板翘曲应力进行研究，证明了无砟轨道翘曲应力可以采用无限大板翘曲应力计算式求解，计算式为

(10)

在进行结构可靠度分析时，轨道板的极限翘曲变形承载力考虑为固定参数，其取值与温度梯度的正负相关：在正温度梯度作用下，轨道板板端产生向下的翘曲变形，CA砂浆层承受来自轨道板翘曲产生的压力[14]，σuq近似等于CA砂浆层的极限压应力，近似取为15 MPa；在负温度梯度作用下，轨道板板端产生向上的翘曲变形，CA砂浆承受由于轨道板翘曲产生的拉力[14]，σuq近似等于CA砂浆层的极限拉应力，近似取为3 MPa[15]。

2.4 正常使用极限状态下CRTS Ⅱ型无砟轨道板体系极限状态函数

桥上CRTS Ⅱ型轨道板的正常使用极限状态需考察纵横向开裂以及轨道板翘曲应力三个方面。轨道板的正常使用状态要求其纵向裂缝宽度不大于允许开裂宽度、横向不开裂以及翘曲应力不大于允许应力。因此，在正常使用极限状态下，各失效模式间的逻辑关系如图3所示，CRTS Ⅱ型轨道板为串联体系。

图3 正常使用极限状态下CRTS Ⅱ型轨道板失效模式间逻辑关系示意

根据等价极值事件原理，串联体系的体系极限状态函数表示为所有失效模式极限状态函数的最小值[16]。因此，正常使用极限状态下CRTS Ⅱ型轨道板体系极限状态函数G(X)表示为

G(X)=min[G1(X),G2(X),G3(X)]

(11)

3 CRTS Ⅱ型轨道板正常使用极限状态下的体系可靠度

3.1 基于高阶矩法的体系可靠度分析流程

由于CRTS Ⅱ型轨道板体系极限状态函数中含有分布未知的随机变量(即横向开裂弯矩允许值Mcr)且需要求解有限元分析模型，因此本文采用易与有限元分析结合且适用于随机变量分布未知条件的高阶矩法[17]，通过编写Mathematica程序，开展CRTS Ⅱ型轨道板的体系可靠度分析。该方法的基本思想是基于随机变量统计矩构建极限状态函数的概率分布，从而直接评估失效概率Pf或可靠性指标β，主要包括如图4所示的两个步骤：首先，计算极限状态函数G(X)的统计矩；随后，使用四阶矩可靠性指标估计失效概率Pf或可靠指标β。

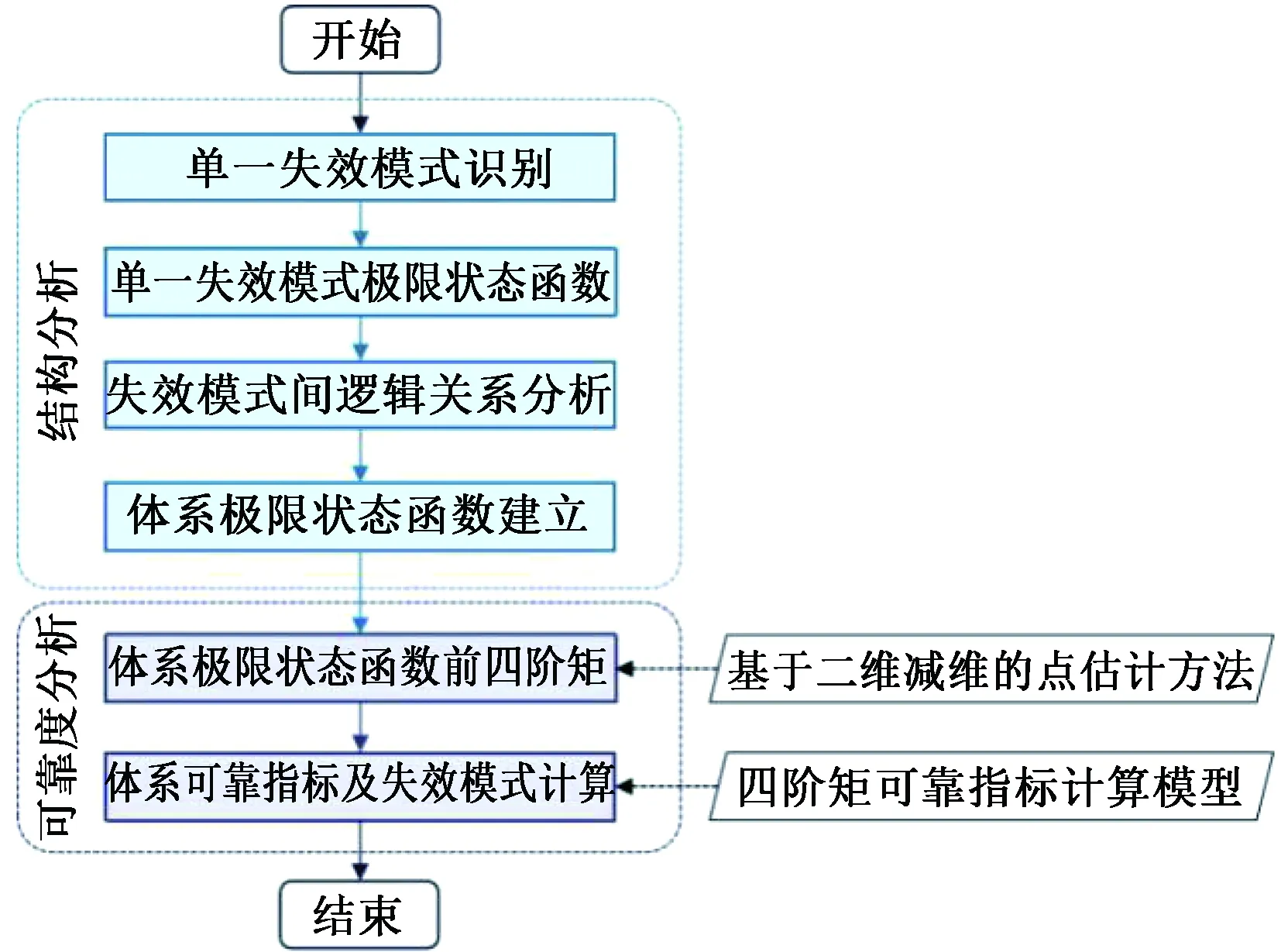
图4 基于高阶矩法的体系可靠度分析流程

体系极限状态函数G(X)前四阶矩(即均值μG、标准差σG、偏度α3G和峰度α4G)的理论表达式为[17]

μG=E1G

(12)

(13)

(14)

式中：EkG为G(X)的第k阶原点矩。

由于EkG的理论求解较为困难，本文采用基于二维减维[18]的点估计方法[19-20]进行分析，EkG近似表达为

(16)

(17)

(18)

式中：m为估计点的个数；ur、uri、urj和Pr、Pri、Prj分别为各估计点在标准正态空间内的取值以和相应的权重；μi为第i个随机变量的均值；T(·)为逆正态变换函数。

基于极限状态函数的前四阶矩中心矩，体系失效概率Pf可以表示为四阶矩可靠指标β4M的函数[17]

Pf=Φ(-β4M)

(19)

式中：Φ(·)为标准正态分布的累积分布函数；四阶矩可靠指标β4M的常用公式为[21-22]

(20)

(21)

(22)

(23)

其中，β2M为二阶矩可靠指标。当偏度α3G和峰度α4G处于式(20)的适用范围外时，可以采用四阶矩可靠指标的完备公式[23]进行求解。

3.2 CRTS Ⅱ型轨道板随机变量统计信息

由于CRTS Ⅱ型无砟轨道板可靠度分析中荷载作用的随机性较大，本文将所有荷载作用关键参数看作随机变量。考虑正常使用极限状态时，CRTS Ⅱ型轨道板荷载的关键参数包括：纵横向列车荷载、列车制动力、温度梯度、整体温度变化、收缩徐变等效温降。纵横向列车荷载的不确定性采用静轮载Pj表示。根据式( 2 )可知，列车的制动力由扣件阻力Fcj折算，列车制动力的不确定性采用扣件阻力Fcj表示。因此，CRTS Ⅱ型板式无砟轨道结构可靠度分析中表征荷载作用随机源不确定性的关键参数为Pj、Fcj、Tg、ΔT、ΔTck。上述关键参数均考虑为随机变量，其统计信息见表2。由于轨道板横向开裂弯矩值Mcr为基于试验确定的值，而试验本身存在着较大的随机性，因此本文中Mcr也作为随机变量进行分析，其统计信息同样列于表2中。

表2 CRTS Ⅱ型轨道板可靠度分析中随机变量的统计信息

3.3 体系可靠度分析

基于建立的CRTS Ⅱ型轨道板体系极限状态函数和随机变量的统计信息，本节采用高阶矩法开展正常使用极限状态下CRTS Ⅱ型轨道板的体系可靠度分析。如表3所示，CRTS Ⅱ型轨道板温度梯度均值μΔT和轴向温度均值μTg的符号均可能为正或负，因此开展轨道板的体系可靠度分析需要考虑温度梯度和轴向温度的四种可能组合情况：

轴向温度和温度梯度的均值均为正(情况一)；轴向温度均值为正、温度梯度均值为负(情况二)；轴向温度均值为负、温度梯度的均值为正(情况三)；轴向温度和温度梯度的均值均为负(情况四)。

由于CRTS Ⅱ型轨道板在正常使用极限状态下的体系极限状态函数为与有限元模型结合的强非线性函数，因此本文使用基于二维减维的七点估计方法计算体系极限状态函数的前四阶矩，计算结果见表3。基于体系极限状态函数的前四阶矩，采用四阶矩可靠度计算模型(式(20)～式(23))可以直接得到可靠度及相应的体系失效概率(式(19))，分析结果也列于表3中。为了研究正常使用极限状态下CRTS Ⅱ型轨道板体系可靠度与单一失效模式可靠度之间的关系，本文使用式( 5 )、式( 8 )、式( 9 )作为纵向裂缝过大、横向开裂以及翘曲失效模式的极限状态函数，采用高阶矩法分析上述极限状态函数的可靠度与失效概率，分析结果列于表4。为探讨高阶矩法在CRTS Ⅱ型轨道板可靠度分析中的适用性，本文采用蒙特卡洛方法(105次模拟)对CRTS Ⅱ型轨道板体系可靠度及单一失效模式可靠度进行了分析，分析结果同样列于表3和表4中。需要注意的是，由于CRTS Ⅱ型轨道板极限状态函数含有限元分析，因此蒙特卡罗单次模拟的耗时较长。这限制了蒙特卡洛模拟的次数(本文采用105次模拟耗时100 h)，因此蒙特卡洛方法无法准确开展小失效概率工况下的可靠性分析。由表3和表4可知：

(1)对于轴向温度和温度梯度的均值不全为负数的情况，正常使用极限状态下CRTS Ⅱ型轨道板体系可靠度均在2.4以上，这表明上述情况下CRTS Ⅱ型轨道板在正常使用极限状态下是可靠的。对于轴向温度和温度梯度的均值均为负数的情况，CRTS Ⅱ型轨道板在正常使用极限状态下的体系可靠度为0.945 7，可靠程度较低。

(2)对于所有的轴向温度和温度梯度组合情况，CRTS Ⅱ型轨道板的体系可靠指标均小于所有适用性失效模式可靠指标的最小值，这说明将单一适用性失效模式独立分析可能会过高估计CRTS Ⅱ型轨道板的可靠度，为结构体系带来危险隐患。

(3)基于高阶矩法得到的可靠度分析结果与蒙特卡洛方法得到的分析结果基本一致，从而证明了高阶矩法在CRTS Ⅱ型轨道板可靠度分析中的准确性。

表3 正常使用极限状态下CRTS Ⅱ型轨道板体系极限状态函数前四阶矩、可靠指标及失效概率

表4 CRTS Ⅱ型轨道板单一适用性失效模式极限状态函数前四阶矩、可靠指标及失效概率

3.4 参数敏感性分析

由于我国高速铁路覆盖地域辽阔，CRTS Ⅱ型轨道板所处环境复杂多变，因此温度梯度和轴向温度都具有较大的变异性。为充分考察不同环境下轨道板的结构可靠度，本节分别分析了温度梯度以及轴向温度作用对轨道板结构可靠度的影响。CRTS Ⅱ型轨道板在正常使用极限状态下的体系可靠指标随温度梯度均值μTg和轴向温度变化μΔT的变化曲线如图5所示，其中μTg的取值范围为-50～150 ℃/m，μΔT的取值范围为-40～40 ℃。

图5 正常使用极限状态下CRTS Ⅱ型轨道板体系可靠指标随μTg和μ△T变化曲线

由图5可知：

(1)当温度梯度均值μTg在-50～150 ℃/m范围内变化时，CRTS Ⅱ型轨道板在正常使用极限状态下的体系可靠指标随μTg的增加呈现出逐渐上升的趋势，且正温度梯度作用下的体系可靠指标明显大于负温度梯度作用下的可靠指标。显然，温度梯度对CRTS Ⅱ型轨道板体系可靠度有明显影响，负温度梯度为更不利工况。

(2)当μΔT较小时，CRTS Ⅱ型轨道板体系可靠指标均随μΔT的增加而增大；当μΔT较大时，体系可靠指标随μΔT的增加基本不变。对于温度梯度均值μTg为-45、90 ℃/m两种情况，体系可靠指标随μΔT的变化趋势由上升到平稳的转折点分别是约-12、-20 ℃。这是由于轴向温度仅会影响纵向裂缝宽度失效模式的可靠指标，随着μΔT的不断增加，该失效模式的可靠指标将达到较大的值，之后该失效模式及体系的可靠度随μΔT的变化将极为平缓。

4 结论

本文研究了CRTS Ⅱ型轨道板所承受的荷载作用及不同荷载作用下轨道板的响应，并采用有限元模型对竖向列车荷载作用下的轨道板弯矩进行分析。分析了正常使用极限状态下CRTS Ⅱ型轨道板各适用性失效模式，得到相应的极限状态函数，建立了CRTS Ⅱ型无砟轨道板的体系极限状态函数。使用高阶矩法分析了CRTS Ⅱ型轨道板在正常使用极限状态下的体系可靠度，并基于参数敏感性分析探讨了温度梯度和轴向温度对轨道板体系可靠度的影响。研究可得到如下结论：

(1)本文提出的正常使用极限状态下CRTS Ⅱ型轨道板体系极限状态函数形式简单，涵盖了轨道板纵向裂缝宽度过大、横向开裂以及翘曲变形三种失效模式，便于工程实际应用。

(2)本文总结的基于矩法的 CRTS Ⅱ型无砟轨道板可靠度分析方法流程，具有计算简单高效的优点，可以与有限元分析模型结合开展无砟轨道体系可靠度分析。分析结果表明正常使用极限状态下，CRTS Ⅱ型轨道板在温度梯度和轴向温度不同时为负数时具有较高的可靠度。

(3)温度梯度和轴向温度对正常使用极限状态下CRTS Ⅱ型轨道板体系可靠度具有较为明显的影响，体系可靠指标随温度梯度的增加呈现上升趋势，随轴向温度的变化呈现出先升后稳的趋势。