基于响应面法的减速器行星架多目标优化研究*

李志远,裴 帮,李学飞,陈 卓,黄晓丹

(郑州机械研究所有限公司,河南 郑州 450001)

0 引 言

作为行星齿轮减速器中的主要构件之一,行星架是行星齿轮传动系统中结构和受力都比较复杂的零件。作为动力的输出构件,行星架承受的外力矩最大,同时其质量和尺寸也是传动系统中最大的[1]。行星架的强度在行星减速器中起着关键的作用,所以对行星架进行强度分析很有必要。

在有限元分析过程中,不同的边界条件会造成不同情况的应力分布状况,所以探讨、分析合适的边界条件是重要的。姜振波、杨瑞锋等人[2]在对采煤机的行星架进行有限元分析过程中,对行星架不同的边界条件方案进行了对比研究。陈器[3]在对盾构机的行星减速器行星架进行仿真分析及优化过程中,将行星架与行星轴装配在一起,使等效应力出现在退刀槽内;通过采取增加圆角的方式减小了其应力集中。

响应面法采用多元多项式或非多项式模型(如Kriging模型)来描述系统自变量和响应特征之间的复杂关系,替代有限元仿真和其他复杂模型。因此,在工程中,采用响应面法可以进行更为有效的设计或计算工作。同时,选择合适的实验设计方法和高精度的响应面模型可以大大缩减优化设计的时间[4]。

要保证响应面模型的精度,对实验设计方法的选取很重要。张令弥、费庆国等人[5]在用于确定性计算仿真的响应面法及其试验设计研究过程中,对常用实验设计方法进行了详细介绍。逯振国、杨素等人[6]采用有限元方法对采煤机行星架质量进行优化分析时,利用响应面分析法,以行星架中的行星轴孔为优化参数,对其质量进行了优化。常涛等人[7]分析了制造加工的过程中的不确定参数对行星架强度的影响,并且对其可靠性也进行了验证。殷国富、陈箭等人[8]基于变密度法插值模型,对行星架进行了结构拓扑优化;在优化结果的基础上,重新设计了新的行星架,并对其可用性进行了验证。

在动力学方面,MCINERNY S A和PARKER R G等人在研究三维斜齿行星齿轮的模态特性时,分析了行星架的振动对失效的影响[9,10]。KELLER J A等人[11]在对行星架进行振动监测进行研究时,对改进的特殊工况下的行星齿轮箱进行了标准参数化诊断分析。BLUNT D M等人[12]用模态分析方法,对行星齿轮传动行星架的疲劳破坏状况进行了研究分析。

在静力学方面,前人的研究过程中,并没有考虑轴承对行星轴的约束,因此,笔者将轴承对行星轴的约束近似为刚性约束,通过宽度与轴承一致刚性支架模拟轴承对行星轴的约束;对比刚柔耦合模型和传统分析方案,选择合理的方案分析,通过建立响应面模型,以便能更高效率地进行多目标优化设计。

1 有限元模型建立

笔者采用2k-h型行星轮系作为研究对象。此型号行星轮系的外齿圈固定不动,通过太阳轮与行星轮的啮合,使行星架输出转矩。

由于参数化建模可使后期优化设计变得极其方便,笔者利用SolidWorks进行参数化建模。

参数化模型如图1所示。

图1 参数化模型

笔者采用Workbench对行星架进行有限元分析,将已经完成的三维模型直接导入Workbench中的Static Structural模块(Geometry)中,并利用Workbench中自带的三维软件Design Model打开,以将行星架中的参数化信息导入Workbench中。

在划分网格前,需要对模型进行预处理。由于圆角的存在会导致划分的网格数量过于庞大,因网格梯度过大而导致计算结果不符合实际。此处,笔者将行星架中非关键部位的圆角删除。

行星架的材料机械性能如表1所示。

表1 材料机械性能

2 方案分析

为分析比较不同的边界条件对行星架的应力与位移的影响,笔者采用两种不同的边界条件对行星架进行有限元分析,并选择其中与实际情况比较接近的情况进行优化设计。

2.1 行星架受力分析

2K-H型行星架传动系统的结构简图如图2所示。

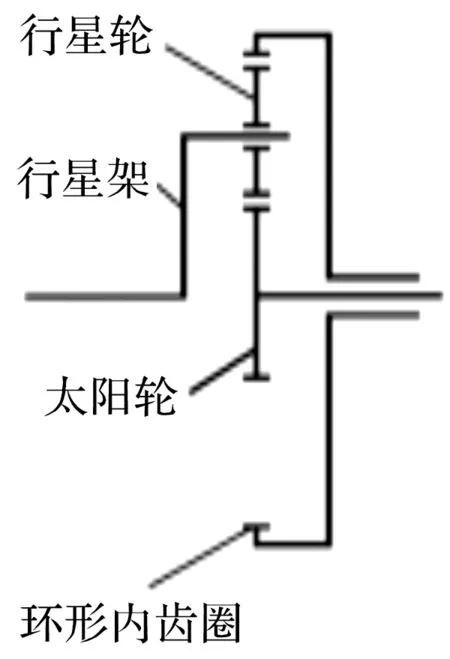
图2 传动结构简图

根据该行星轮系的设计参数,输出功率约为P=3 728.11 kW,输出转速为114.95 r/min,则其输出转矩为:

(1)

2.2 方案一仿真分析

方案一。采用直接对行星架进行加载的方式,通过行星架的输出扭矩计算出行星轴中心轴所在圆的扭矩。

行星架受力分析如图3所示。

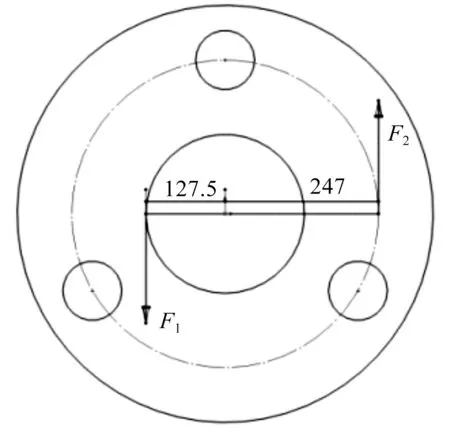
图3 行星架受力图

由于已知输出转矩309 730 N·m,根据力矩平衡可得:

(2)

由F2可知，每个行星轴孔的受力为：

(3)

笔者使用Workbench中的轴承力功能来模拟轴承对轴承孔的加载效果,并对每个孔建立独立的局部坐标系以控制方向(方向为轴承孔所在圆的切线方向),边界条件加载后对其进行求解,最后得到应力云图如图4所示。

图4 应力云图

得到位移云图如图5所示。

图5 位移云图

2.3 方案二仿真分析

方案二。采用更加贴合实际的加载情况,用刚柔耦合模型对行星架进行分析。

之所以采用刚柔耦合模型,是因为笔者关注的应力是行星架,而非刚性支架,故将其设置为刚性体,使其只传递力的作用而不受力。这在一定程度上减少了网格的划分数量,提高了计算的效率;

此外,由于轴承的内齿圈与行星轴为过盈配合,笔者将行星轴与轴承内圈的配合视为刚性约束,且忽略齿轮啮合刚度。在此前提下,将齿轮传动简化为一个刚性支架。

笔者将刚性支架、行星轴与行星架装配在一起,得到行星架装配图,如图6所示。

图6 行星架装配图

笔者将其导入Workbench中进行预处理,并进行边界条件的施加。首先,将支架设定为刚体,其与行星轴、行星轴与行星架的之间的接触按照全部实际的接触状态,即有摩擦接触处理。在接触的设置中,由于存在刚体,刚体只能作为目标面设定;

此外,由于Workbench中的刚体无法施加固定约束,为达到固定的目的,笔者对刚性支架施加远程位移约束,并将远程位移6个方向的自由度全部设置为0,以达到固定约束的效果;

最后,在行星架的输出端施加扭矩。

在涉及摩擦的有限元分析中,为保证精度,笔者将Workbench自适应网格功能关闭。在该模型中,将全局平均的尺寸控制在15 mm,在需要关注的部位,即行星轴与行星架的接触部位进行局部细化网格,并将网格增长率设定为1.1,使网格梯度尽量减小。

由于笔者已将支架设定为刚体,在有限元分析中,对刚体划分网格仅仅限于接触部位。

方案二最后得到的位移云图如图7所示。

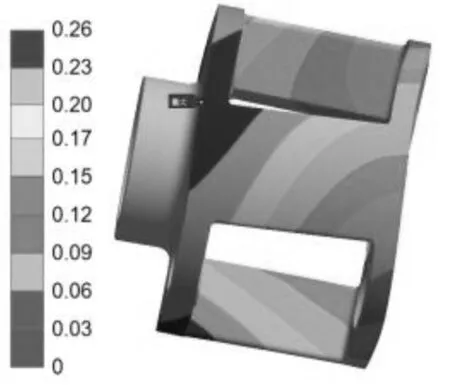
图7 位移云图

最后得到的应力云图如图8所示。

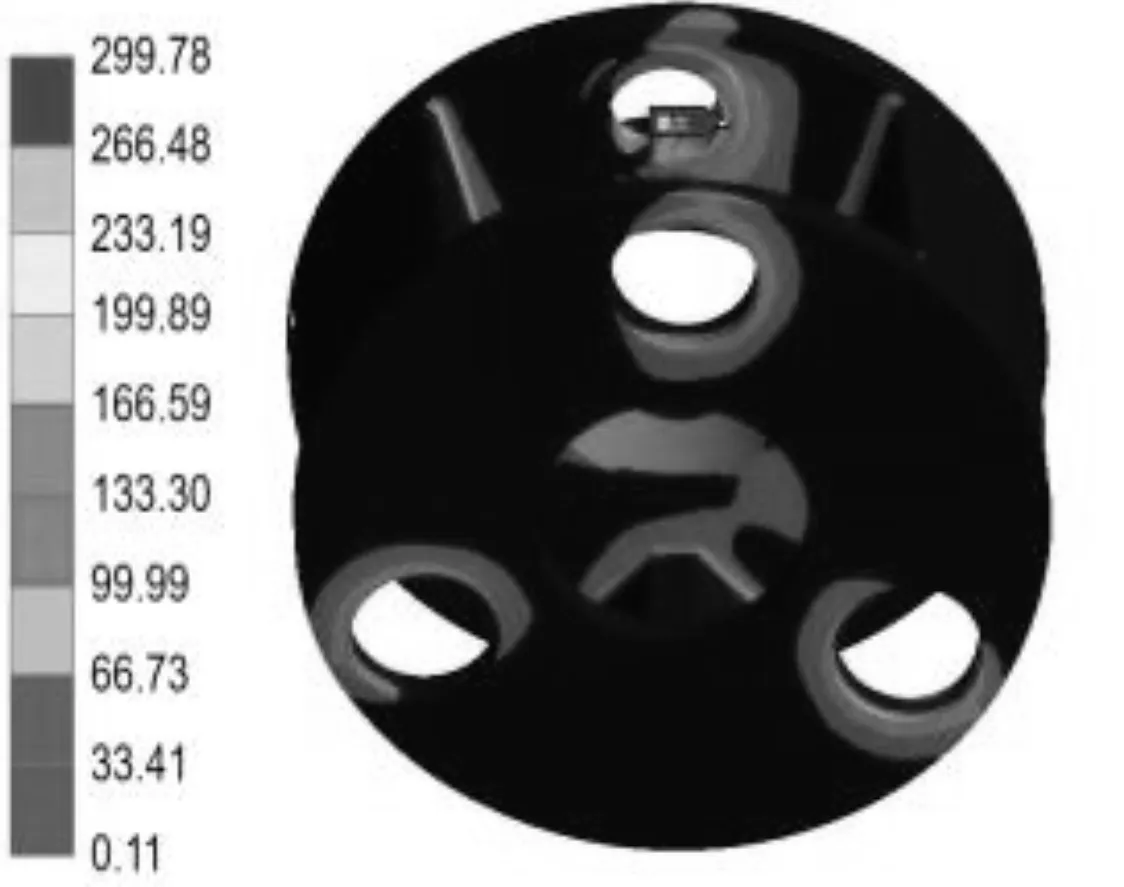
图8 应力云图

2.4 方案对比分析

方案一与方案二的最大应力柱状图和最大变形柱状图对比结果,如图9所示。

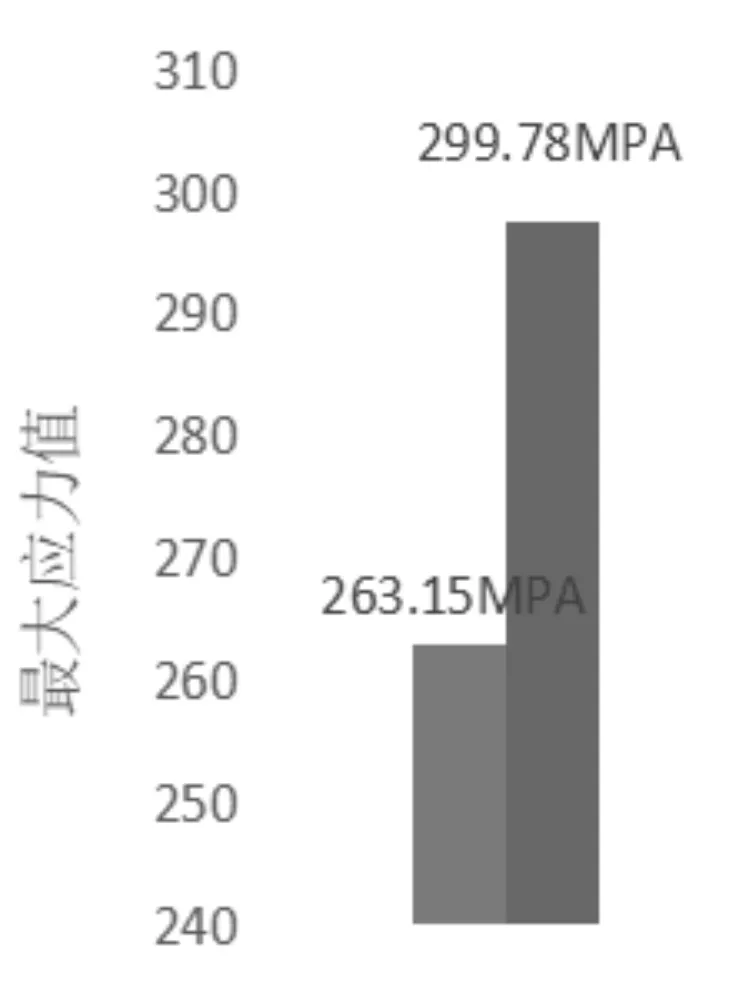
图9 方案对比图

方案一的最大应力值小于方案二的最大应力值,原因是由于方案一将3根行星轴所受的力均匀地分配到6个行星轴孔上,没有产生行星轴与行星轴孔的接触导致的应力集中现象,故其最大应力值小于方案二;

方案二的最大变形值小于方案一,原因在于:(1)方案一每个轴孔受力均匀,而输入端又缺少约束,导致方案一的输入端的变形过大;(2)方案二用来模拟轴承约束的刚性支架对行星轴有一定的约束作用。在实际情况中,轴承内圈对行星轴的约束使其阻挡了行星架的转动,因而也就没有输出转矩;(3)方案二的负载大多集中在输出端,且受到行星轴的反作用力。

3 多目标优化

3.1 数学模型建立

为了提高行星架的静力学性能,笔者采用多目标优化的方法对行星架的关键参数进行优化设计,以提高计算效率。

多目标优化设计问题的数学模型[13]为:

FindX=[X1,X2,X3…Xn]∈Rn

Minf(X)=f(x1,x2,x3…xn)

(4)

式中：FindX—求解的最优解；X—设计变量；xn—第n个设计变量元素；Rn—设计变量的可行域；f(x)—目标函数；S.T—约束函数；σi(X)—第i个不等式约束；τl(X)—第l个不等式约束。

3.2 响应面模型建立

响应曲面分析设计方法是一种利用合理的实验设计方法,通过实验得到相应的数据,运用多元二次回归方法拟合因素与响应值之间的关系,通过对回归方程的分析寻求最优解,从而解决多变量问题的统计方法[14]。相对于直接优化方法,响应面法因为不需要每次都进行有限元计算,所以其计算效率相对更高。

经过笔者对比验证可知,方案二的边界条件较方案一更贴合实际,为更理想的优化结果。因此,笔者将行星轴和行星架装配在一起,进行装配体的优化。

行星轴的剖视图如图10所示。

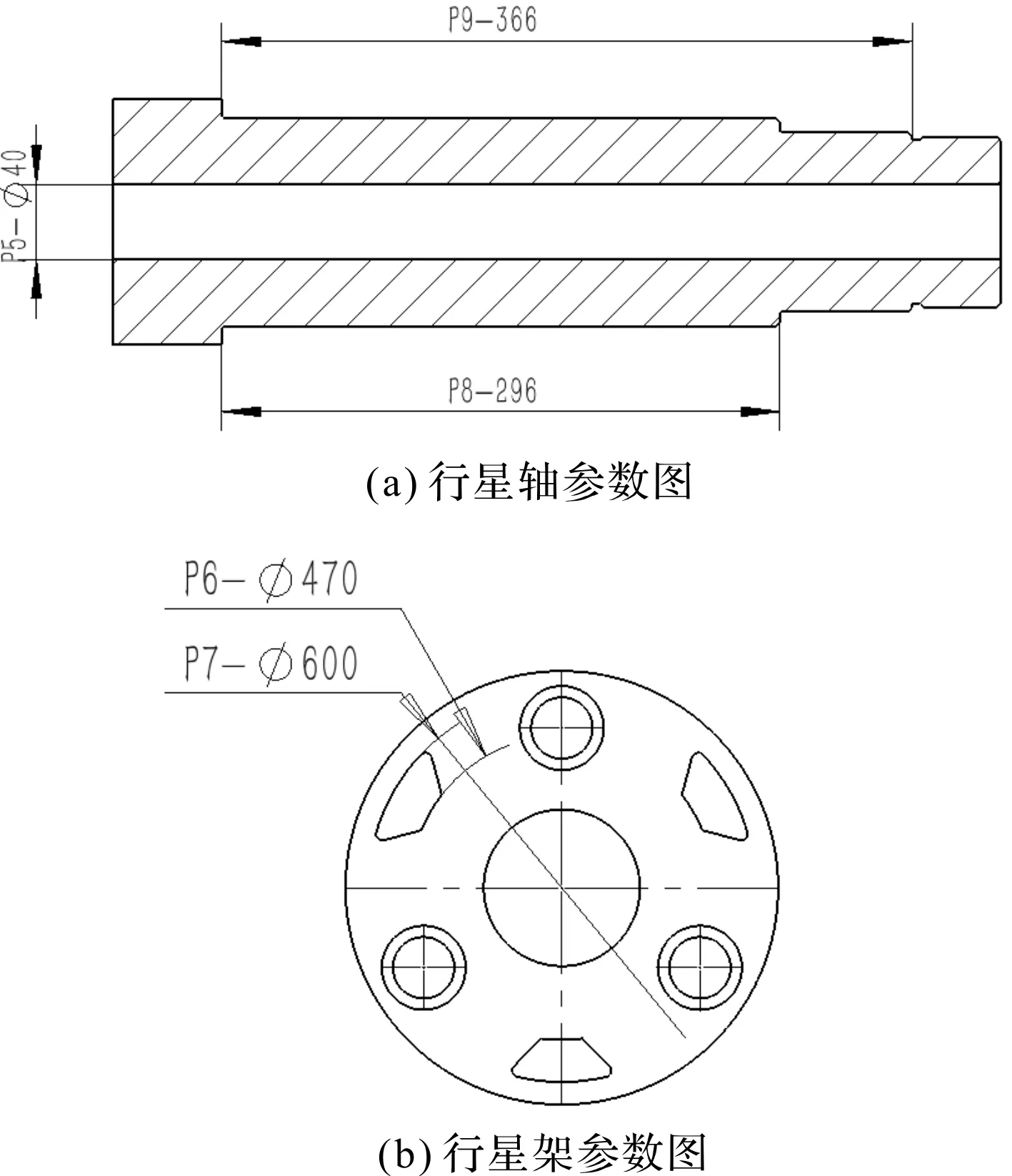
图10 行星轴与行星架参数图

图10中,轴肩长度(P8)、接触长度(P9)和通孔直径(P5)为本次要优化的行星轴参数。

对方案二进行分析可知,行星架的3根三角柱的受力较小,故笔者对三角柱进行优化,即将三角柱挖成通孔,并将内圆直径(P6)和外圆直径(P7)作为优化参数,将行星轴孔应力(P1)、输入端应力(P2)、总变形(P3)和行星架质量(P4)作为结果输出。

参数优化范围如表2所示。

表2 参数优化范围

该实验设计的目的是在样本区间合理地选择每个随机采样点,通过实验得出样本点的响应值,为响应面的建立提供原始数据[15-17]。笔者采用Central Composite Design实验设计方法对样本进行计算,然后利用Kriging响应面模型对样本数据进行拟合。

拟合优度图如图11所示。

图11中,由设计点计算出的观察值和利用响应面拟合出的预测值高度吻合,该结果表明,响应面模型的可信度良好。

最终,笔者得到了响应曲面(包括:最大变形响应面和最大应力响应面),如图12所示。

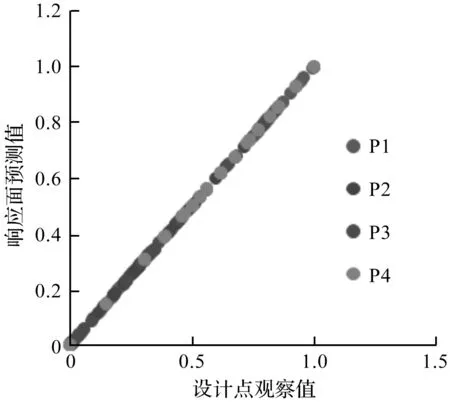
图11 拟合优度

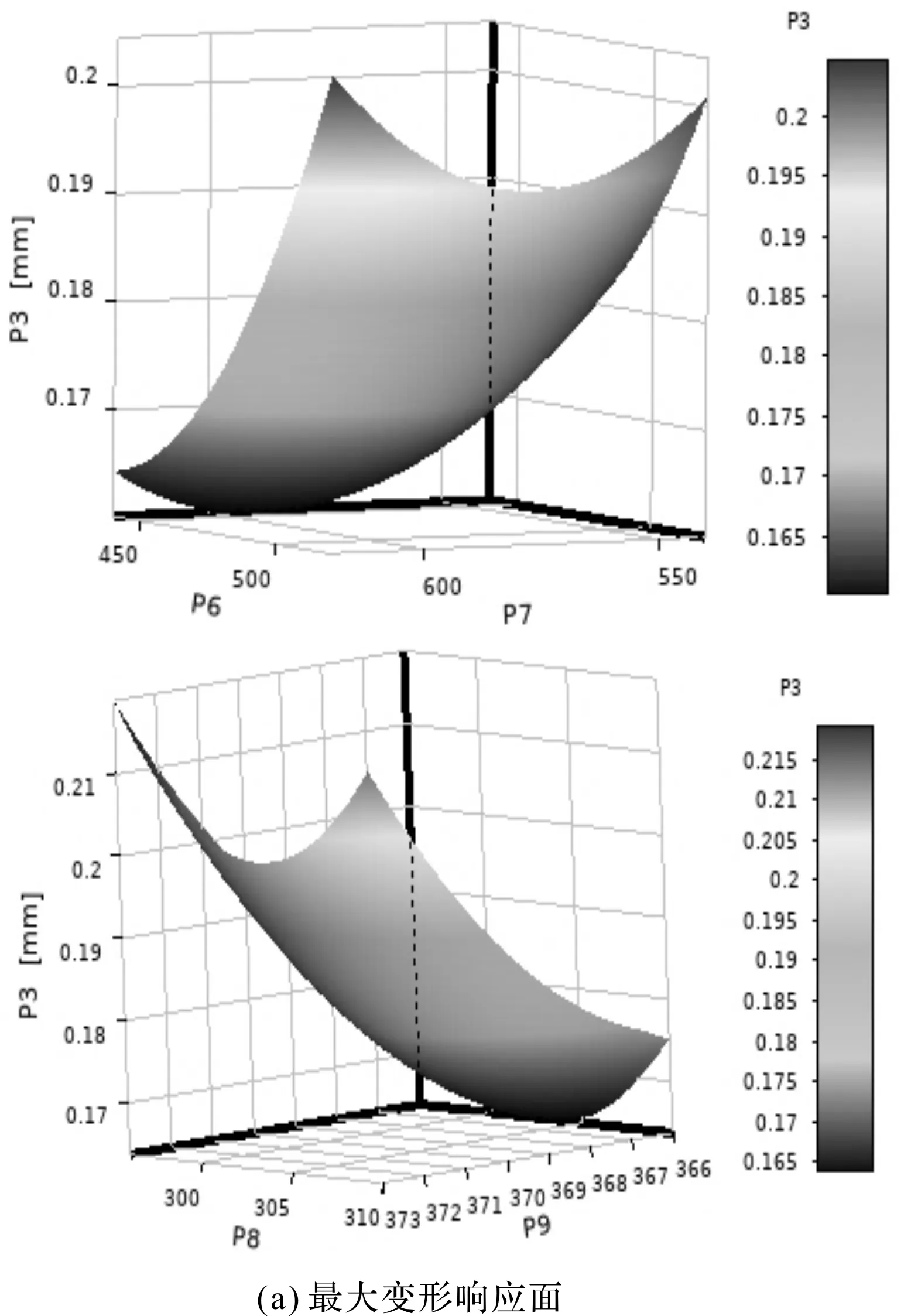
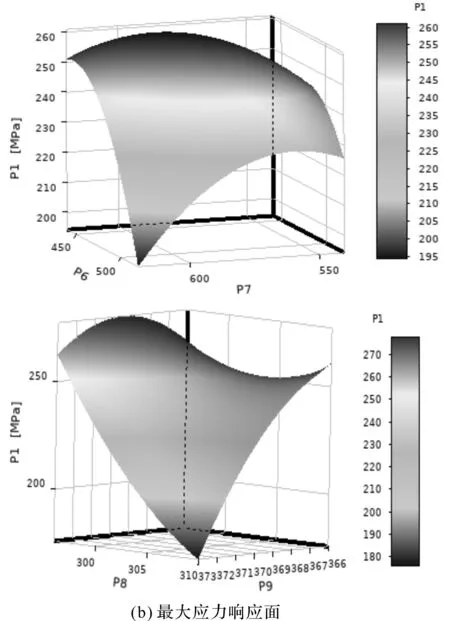
图12 响应曲面

图12中,响应面反映出了各个参数对输出参数的响应程度。

由图12(a)可知:P7和P8在当前取值条件下与行星架最大变形呈二次函数关系,当以最小变形为目标寻求最优解时,候选点的值会选在黑色区域部分;

由图12(b)可知:P8与P9相对于P6与P7对最大应力的影响更大,P6、P7、P8、P9的增加可使最大应力减小,但会导致更大变形。在满足强度的情况下,可增加上述参数以减小变形。

完成响应面的建立后,笔者通过设置优化目标得到3个候选点,如表3所示。

表3 候选点数据

3.3 静力学验证

笔者根据优化后的数据重新建模,并按照之前相同的边界条件进行计算与验证,最后将计算结果与响应面的预测结果(候选点3)进行比较,其结果如表4所示。

表4 响应点验证

由表4可知,该响应面的预测精度良好,可以准确地反映不同参数组合的实际输出结果。

笔者将优化前的数据和优化后的数据进行对比,其结果如图13所示。

由表13可知:行星架的最大应力由299.78 MPa降低为269.35 MPa,减小了10.1%;最大变形量由0.26 mm降低为0.17 mm,减小了34.6%;行星架的质量由开始的413.58 kg降低为310.81 kg,减小了24.8%。

图13 最终优化对比

由此可见,该行星架综合优化的效果显著。

4 结束语

笔者通过两种不同的方案对行星架进行了静力学分析,并筛选出了最优方案,随后对行星架装配体的刚柔耦合模型的关键参数进行了CCD抽样分析,并拟合出响应面最优解;最后,对该最优解进行了验证。

研究结果表明:

(1)基于刚柔耦合模型的方案二更加贴合实际,且最大应力位置在行星轴和行星轴孔的接触位置;

(2)行星架的输入端和输出端的轴孔受力不均匀,且大部分应力集中在输出端,输入端面板的受力偏小;

(3)行星轴上的通孔对其最大应力的影响较为显著,且为非线性关系;当轴刚度小于临界值时,通孔直径的增加会导致其最大应力减小,反之则会导致其应力增大;

(4)通过建立响应面模型,对需要修改的参数进行多目标寻优,得出最优解,并对最优解进行了静力学验证,其结果表明,响应面精度在误差范围内,该最优解结果可以接受;并且以最优解为最终优化方案,取得的优化效果最为显著。

综上所述,在保证响应面精度的情况下,基于响应面法的参数优化零件的优化效果良好,特别适用于无法通过手动计算强度的零件。

在后续的研究中,笔者将对复杂结构零件进行全参数优化,以实现其轻量化设计的目的。