一种基于电磁弹簧的智能减振器设计与研究*
卫洪涛,宋雪柯,王振宁,李亚鹏,马 竞,王 鹏
(1.郑州大学 力学与安全工程学院,河南 郑州 450001;2.郑州大学 机械与动力工程学院,河南 郑州 450001;3.上海第二工业大学 智能制造与控制工程学院,上海 200120;4.吉林大学 汽车工程学院,吉林 长春 130025)
0 引 言
振动控制一直是工程中的热门话题。在很多工况中,振动的产生不利于设备的正常运行。较大的振动还常伴有巨大的噪音[1],会对人的身心健康造成伤害,因此,人们尝试使用了很多种办法来减弱或消除工程中的干扰振动。
从振动问题提出至今,有关于减振方式的研究已经得到了很大的发展。按是否有外界能源输入,可把振动控制分为:被动式、半主动式、主动式和混合式四大类[2]。其中,被动式控制是最早的控制方法。
随着科技的进步,参数可调式减振器逐渐成为了大多数学者研究的焦点。参数可调一般有3种形式,即刚度可调、质量可调及阻尼可调:
(1)刚度可调。它包括3种结构,即悬臂梁结构、摆杆式结构、电磁式结构。李化[3]设计了基于电磁驱动的悬臂梁式吸振器,通过改变梁的有效长度来改变吸振器的固有频率。赵国迁[4]提出了一种倒立式单摆动力吸振器,通过改变单摆的有效长度,以此来改变吸振器的固有频率。孙志卓[5]对电磁式动力吸振器进行了研究,并且设计了基于电磁力的电磁式动力吸振器;
(2)质量可调。它分为改变液体体积、增加质量块等方法;
(3)阻尼可调。它应用了多种新型材料,如磁流变材料、电流变材料、记忆合金、压电材料等。孙洪鑫[6]进行了磁流变式调谐液柱阻尼器振动控制理论研究,并且进行了相关的试验。李斌等人[7]设计了一种电涡流耗能动力吸振器,并且进行了相关的试验研究。
国外学者也对减振机构进行了大量的研究。BONELLO P等人[8]用压电材料使悬臂梁变形,设计出了一种智能的机电减振装置。DAVIS C L等人[9]则依靠陶瓷压电元件,提出了一种能改变减振器刚度的固态压电减振器。WILLIAMS K等人[10]应用镍钛记忆合金材料,设计出了一种靠温度智能调节的智能减振器。LIU J等人[11]提出了一种通过在线调整电磁体的电流,以此来改变刚度的智能减振装置。
目前,国内外研究者们所提出的减振器结构有很多种,但都存在一定的弊端。比如,改变刚度的方法大多数采用步进电机带动丝杠作为作动器[12-13],丝杠在振动过程中会产生磨损,造成其精度的下降,并且其还具有一定的延迟性。电磁式动力吸振器的结构过于复杂[14],并且还难以加以控制。通过改变液体的体积来改变质量的方法,也存在结构复杂的问题[15],并且很多辅助装置还带来安装不便的问题。采用智能材料制作的减振器更是存在成本高、价格昂贵的问题,不适于推广应用。
除此之外,在目前所查到的文献中,并没有减振器具备自主调节自身频率,以适应多种工况的智能减振功能。而能够自主调节频率的减振器可以在较宽的频带上达到最优的技术指标,在性能和经济性上都具有较大的优势。
基于以上分析,笔者设计一种基于电磁弹簧的减振器。
1 电磁弹簧
1.1 结构设计
电磁弹簧由3块圆盘形状的永磁铁、连杆、圆筒形衔铁和线圈组成。
电磁弹簧的结构图如图1所示。

图1 电磁弹簧结构图
图1中,固定永磁铁分别与圆桶上下底固定在一起,移动永磁铁与连杆固连。在其振动过程中,连杆可以带动移动永磁铁在圆筒中上下移动,2块固定永磁铁磁极方向相同,与移动永磁铁磁极方向相反;
线圈缠绕在导磁率低的桶壁外侧,缠绕位置与移动永磁体可移动的空间范围相对应。在减振过程中,线圈中通入直流电流;
电磁弹簧的刚度由主刚度k和附加刚度k1组成。其中:(1)主刚度由固定永磁铁与移动永磁铁之间的斥力产生,通过改变固定永磁铁之间的磁间距大小可以改变主刚度的大小;(2)附加刚度由线圈中的电流产生,附加刚度的大小由线圈中的电流大小决定,附加刚度的正负由电流的方向决定。
1.2 刚度分析
笔者首先对电磁弹簧的主刚度进行分析。通过观察图1中永磁体的排列方式可知,固定永磁铁对移动永磁铁的作用力为斥力。
在不考虑重力的情况下,移动永磁铁处在磁间距中间位置时,为受力平衡位置,上下固定永磁铁给移动永磁铁的作用力分别为F1、F2,且F=F1+F2=0(F为移动永磁铁受到的合力)。
当移动永磁铁离开平衡位置后,令合力表达式为:
(1)
式中:α—多项式系数;z—永磁铁移动的距离;m—多项式最高次幂。
为了确定这些参数,笔者采用Maxwell软件,对移动永磁铁在磁间距中振动的受力情况进行仿真分析。
在振动过程中,移动永磁铁受力的仿真模型如图2所示。
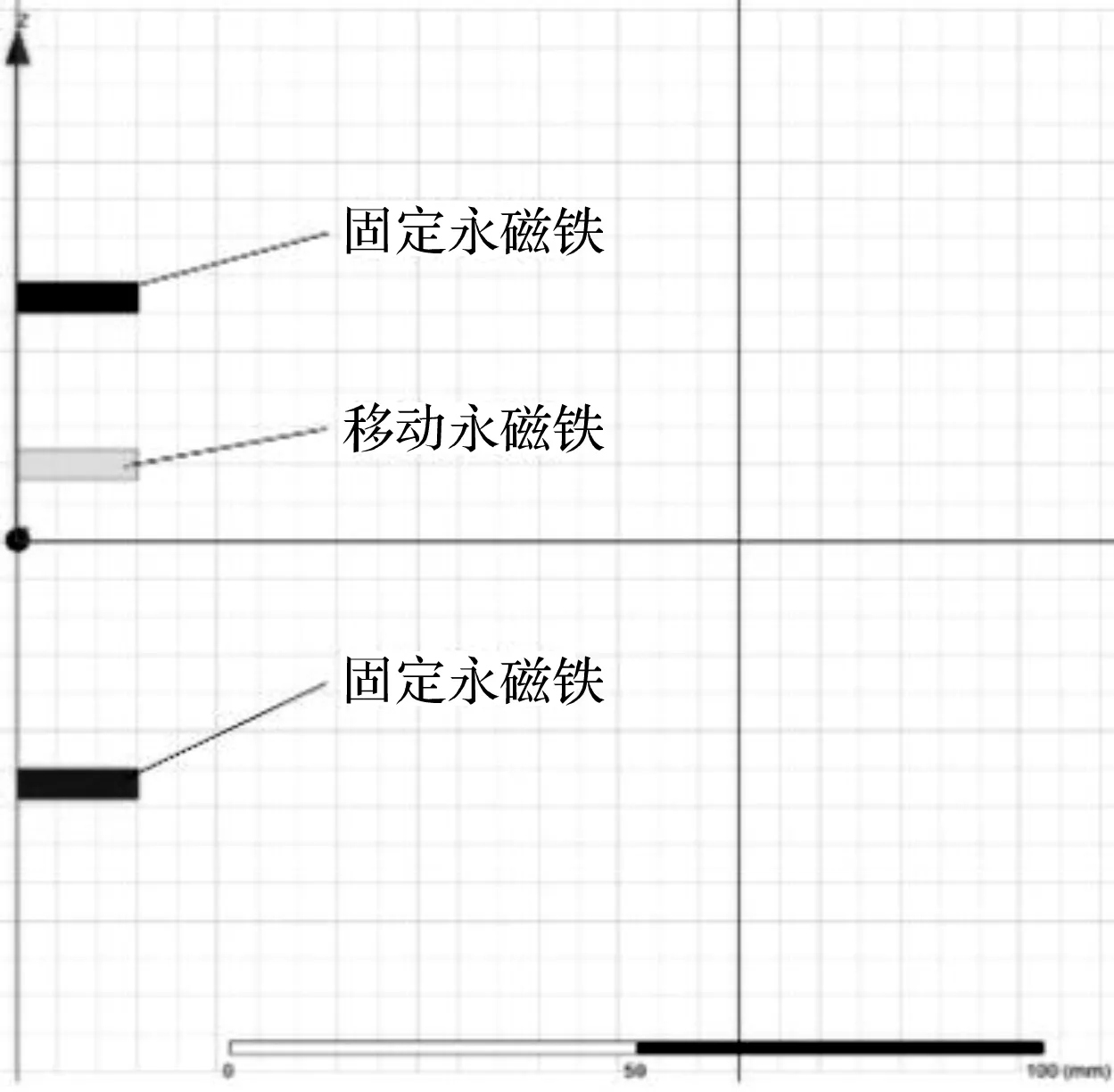
图2 移动永磁铁在振动过程受力仿真模型
图2中,永磁铁选用具有强磁性的钕铁硼材料,其直径30 mm,厚度4 mm,磁间距60 mm,即为永磁铁之间的距离。设定Maxwell分析类型为Maxwell 2D,设计柱坐标系分析类型Cylindrical About,求解器为Magnetic栏下的Magnetostaic求解器,通过构建正确的几何模型,将移动永磁铁的移动距离参数化。
受永磁铁厚度的影响,移动永磁铁的实际移动距离为2 mm~58 mm,从2 mm至58 mm,每1 mm计算一次结果。
电磁弹簧主刚度的仿真分析结果如图3所示。

图3 电磁弹簧主刚度仿真分析结果
对数据进行不同次方拟合,可得到:
y=-2.416 6x+73.335
(2)
y=-0.004 2x3+0.371 5x2-11.517 4x+125.091 3
(3)
y=-6.812 44×10-6x5+0.001 019x4-0.059 96x3+
1.729 531x2-25.635 2x+171.657 3
(4)
式中:y—永磁铁的移动距离。
由图3和拟合数据可知:对离散数据进行5次方拟合的结果已经非常精确,拟合决定系数R2为0.998 6;3次方拟合结果也可令人满意,拟合决定系数R2为0.901 6;
由离散数据的分布趋势可以看出:移动永磁体在磁间距为60 mm空间内大幅度运动时,电磁弹簧刚度总体呈非线性;当移动永磁铁在平衡位置附近小幅度运动时,电磁弹簧刚度具备近似线性性质。
接下来,笔者对电磁弹簧与电流之间的关系进行讨论。
基于电磁感应理论可知,通电线圈中间会产生磁场,附加磁场会对圆桶内部永磁铁磁场产生增强或减弱的作用,从而改变电磁弹簧的刚度。为了使电磁弹簧刚度线性化,笔者在上述模型中加入电流条件,将磁间距缩小为10 mm,并对移动永磁铁的振动过程进行仿真。
在振动过程中,有电流作用下的移动永磁铁的受力仿真模型如图4所示。
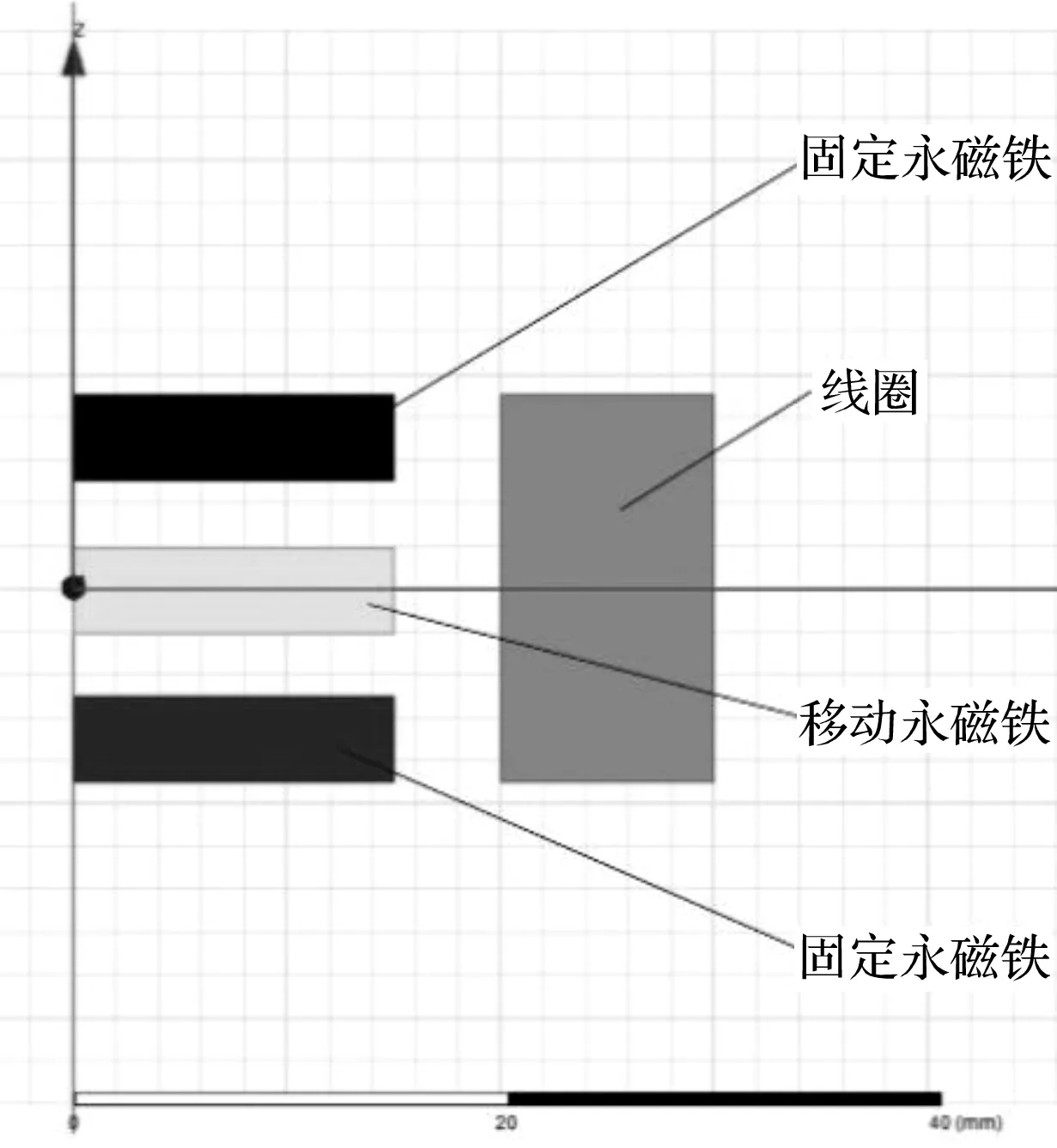
图4 有电流作用下的移动永磁铁受力仿真模型
为了不失一般性,笔者将电流设定为6个挡位,即0~5 A。其中,0 A时即线圈中没有电流,附加刚度为零。
仿真过程与主刚度的类似,增添线圈对其施加边界条件及激励,将电流值参数化,从0 A~5 A,每1 A计算一次结果。
笔者对仿真数据进行线性拟合处理,得到附加刚度k1与电流i之间的关系,如表1所示。
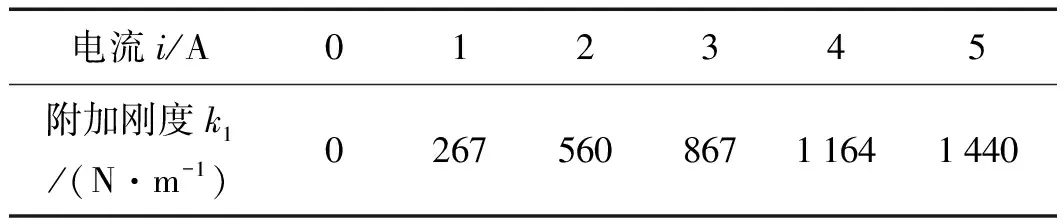
表1 附加刚度与输入电流的关系
笔者对拟合数据进行分析发现,附加刚度与电流有显著的线性关系。
附加刚度与电流的关系如图5所示。

图5 附加刚度与电流的关系
拟合决定因子R2为0.999 5,附加刚度k1与电流i之间的关系为:
k1=291.37i-12.095
(5)
在磁间距为10 mm时,仿真的电磁弹簧主刚度为38 053 N/m。对数据进行处理得到电磁弹簧的总刚度k与电流的关系为:
k=38 053+291.37i-12.095
(6)
2 电磁弹簧模型
笔者设计的智能减振器的刚度由电磁弹簧提供。根据动力吸振器原理可知,减振器刚度线性化程度对其减振性能有显著影响。
由图3可知,电磁弹簧的刚度为非线性,且非线性程度与磁间距密切相关。为了确保电磁弹簧刚度的线性化,笔者对不同磁间距电磁弹簧模型进行仿真;设智能减振器在工作的过程中,振子在平衡位置附近3 mm的空间内振动,在磁间距10 mm~80 mm的范围,每0.1 mm采样一次,用Maxwell软件进行仿真,对仿真数据进行线性拟合。
不同磁间距智能减振器的主刚度拟合对比图如图6所示。
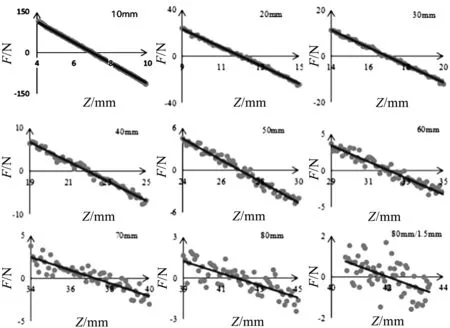
图6 不同磁间距智能减振器的主刚度拟合对比
从图6中可以明显看出:磁间距越小,刚度的线性化程度越高;随着磁间距的增大,不仅刚度降低,非线性也凸显出来。
不同磁间距的电磁弹簧的刚度及拟合决定因子如表2所示。
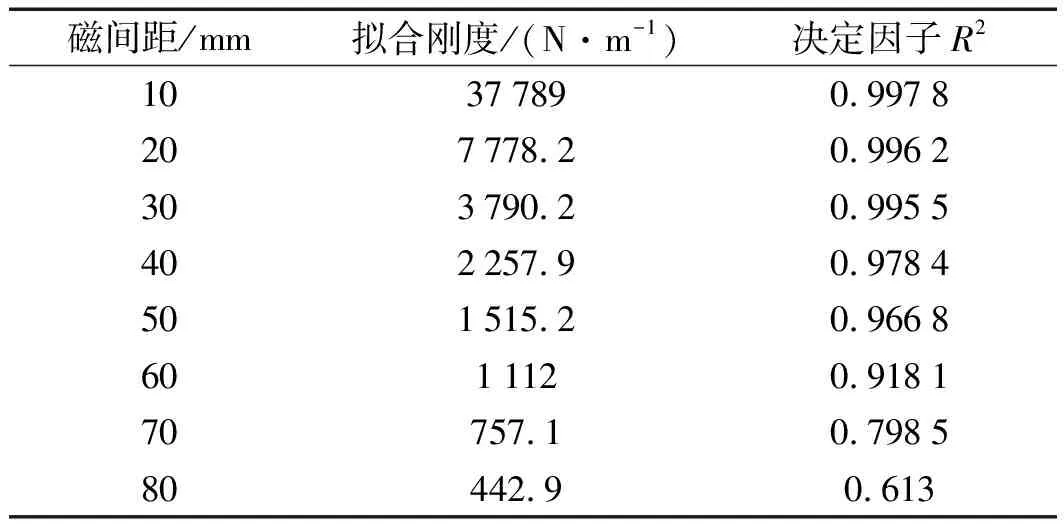
表2 不同磁间距智能减振器的拟合刚度和决定因子
表2中,在磁间距30 mm以内,随着磁间距增大,刚度呈急速下降趋势,刚度线性化程度很高,R2都可达到0.995以上;在磁间距在30 mm~50 mm时,刚度线性化程度降低,R2减小但仍达0.96以上,仍具有较好的线性化程度;当磁间距在80 mm时,R2达到0.613,刚度几乎失去了线性性质。
为了验证磁间距在80 mm时,振子在平衡位置附近的刚度线性性质,笔者假设振子在平衡附近1.5 mm的空间振动,每0.05 mm采样一次。该实验数据及线性拟合结果如图6中最后一幅子图所示,其拟合决定因子为0.323。
仿真结果表明:当磁间距增大到一定程度时,振子在平衡位置附近振动,其刚度线性化程度也很低,此时智能减振器几乎失去了减振效果;另一方面,由于移动永磁铁自身有厚度,且必须有一定的运动空间,所以磁间距不能太小。
综上考虑,笔者确定智能减振器中的磁间距取值范围为10 mm~50 mm。
除了刚度参数外,阻尼系数对智能减振器的减振功能也有很大影响。笔者设计的减振器阻尼由两部分组成:(1)由磁铁相对运动产生的涡流阻尼;(2)由振子和桶壁之间相对运动摩擦引起的阻尼。其中,前者不可避免,后者可通过增加桶壁内径的办法消除,但桶壁内径过大会对附加刚度造成影响。因此,笔者确定桶壁与振子之间的间距为1 mm~2 mm。
3 基于电磁弹簧的智能减振器
3.1 减振器设计
减振器的参数有质量、刚度和阻尼[16]。由动力吸振器的原理可知,当减振器的固有频率与被减振物体的振动频率相等时,减振效果最优,即主系统的振幅达到最小。智能减振器的概念是指减振器可以根据激振力的频率变化自动调节自身参数,使减振器在不同工况下都达到最优减振效果。笔者所设计的智能减振器基于电磁弹簧的刚度可自动调节,电磁弹簧为减振器的刚度元件。
智能减振器由两部分组成,即减振器本体和减振器控制系统。减振器控制系统主要分为感知、控制、执行3个模块。
控制模块控制逻辑流程图如图7所示。
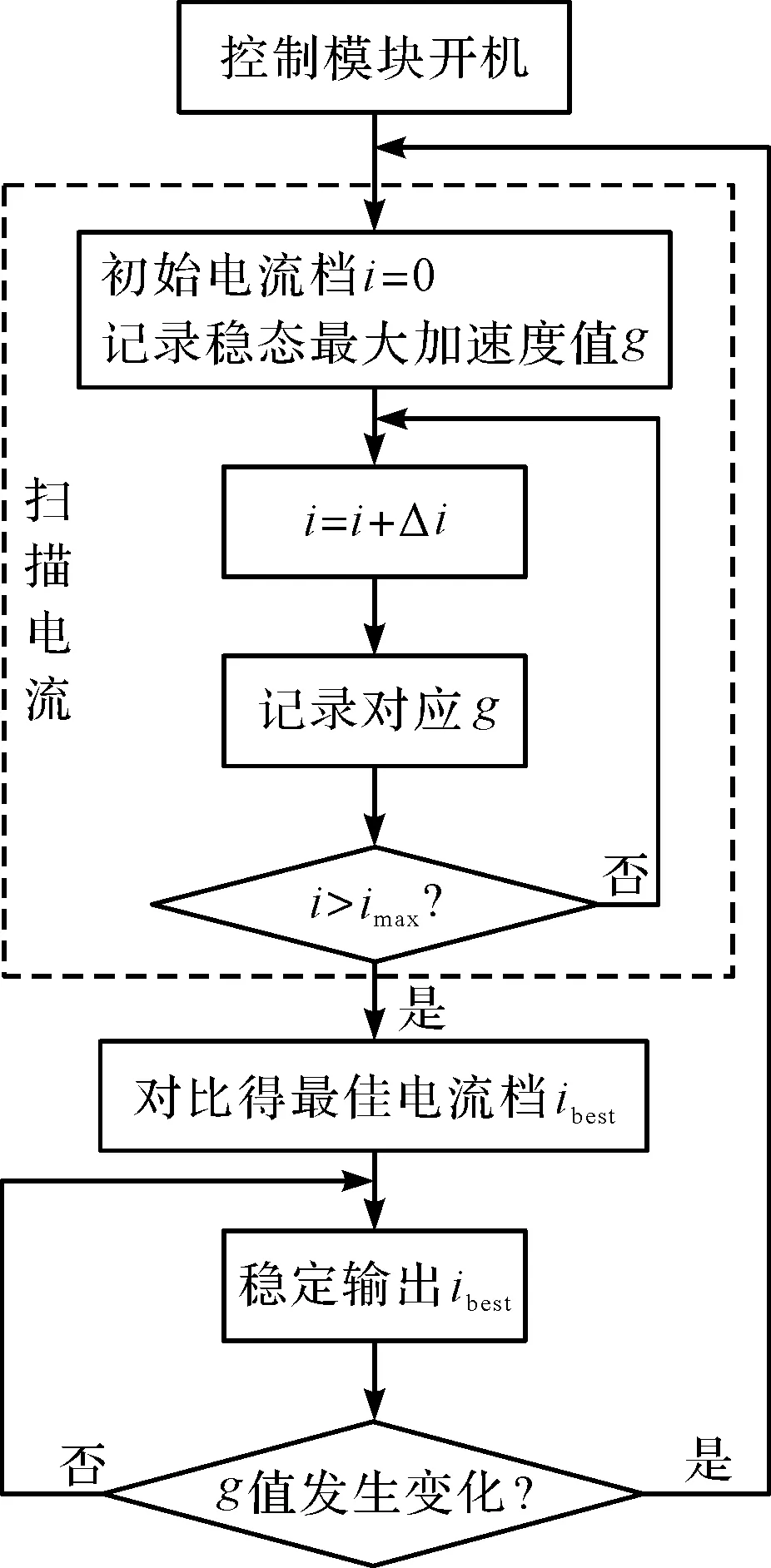
图7 控制模块控制逻辑流程图
图7中,感知模块采用的是JY901九轴加速度器,其作用是实时采集被测物体的振动加速度的值,并将获取的信息传递给控制模块;控制模块采用的是AVR ATMEGA328单片机,其作用是控制扫描输出电流的流程,同时进行减振效果对比,将得到的最佳输出电流信息传给执行模块;
执行模块采用的是Z6005S直流稳压电源模块,其作用是稳定输出最佳的稳流电流,从而改变智能减振器的刚度,即改变智能减振器的固有频率。
具体的智能减振器系统实物如图8所示。

图8 智能减振器系统实物
3.2 减振器变频机构数学模型
3.2.1 永磁铁之间相互作用
永磁铁产生的磁场强度与其尺寸、材料等参数有关。一般来说,对于边长为l×w×h的长方体,磁铁表面极密度σ=±M。
沿永磁铁表面轴线方向距离为z处的磁感线密度为:
(7)
由于许多因素会影响永磁铁的生产,其磁性可能会有所不同。因此,永磁体的特性通常是通过实验来确定的。为了识别磁化强度M,笔者使用直流磁强计在磁极面和永磁铁中心线上测量磁通量密度。
一般情况下,两块永磁铁之间的磁力可以近似表达为:
F0=αB2A
(8)
式中:α—方程的系数,通过实验确定;A—永磁铁相对面的有效面积。
3.2.2 线圈磁场对永磁铁的作用力
中间永磁体在线圈磁场中的受力情况,可将其等效为一个线圈来计算[17]。
对于单个的圆形电流环,其在磁场中的受力为:
dF=KmdS×B=(M×en)dS×B
(9)
式中:Km—永磁体磁化后产生的磁化面电流密度;en—永磁体外表面的单位法向量。
由于只有径向的磁场会产生沿轴向的安培力,永磁铁所受的安培力为:
dF=Br·MdS=Br·MRdθdz
(10)
式中:Br—线圈在永磁体每个电流环处产生的径向磁感应强度。
径向磁感应强度Br可由下式得到:
(11)
式中:α—铁芯大系数;R2,R1,L,d—线圈外径、内径、长度、漆包线线径;r—线圈中心到场点的位矢;Br—线圈在永磁体每个电流环处产生的径向磁感应强度。
由于永磁体本身也可以等效为一个线圈,M可以通过实际测量磁感应强度,并利用下式计算得到:
(12)
(13)
式中:Bz—永磁铁充磁方向的磁感应强度;r0,z0—测点在柱坐标系中的坐标;r,t—永磁体的半径和厚度。
将式(8,13)联合,并沿永磁铁厚度方向积分,可以得到永磁体在线圈磁场中的受力,即:
(14)
3.2.3 电磁弹簧总刚度
将两部分作用力进行叠加,可以得到中间永磁体一面所受到的作用力,即:
(15)
设两侧线圈间距为D,笔者将线圈磁场和固定永磁铁磁场对中间永磁体的作用力相加,得到总的恢复力,并将其对位移z求导,可以得到电磁弹簧的总刚度,即:
(16)
4 实验及结果分析
4.1 实验测试
接下来,笔者通过搭建测振平台,对智能减振器的减振性能进行测试。
测试系统示意图以及仪器安装位置如图9所示。

图9 智能减振器试验系统
图9中,由于被减振的简支梁的一阶频率为42 Hz,笔者在许可的范围内对磁间距进行调整,可以计算出,当选取电磁弹簧主刚度为2 000 N/m时,加上电生磁力产生的刚度,可以使得减振器的固有频率变化范围包含42 Hz。
根据表2可知:当刚度为2 000 N/m时,磁间距在40~50之间,R2在0.96以上,可以满足所需线性关系,笔者故选取2 000 N/m作为减振器的主刚度,振子的质量为0.03 kg。
由式(6)可知,智能减振的总刚度与电流的关系为:
k=2 000+291.37i-12.095
(17)
在设计过程中,为了简化程序,在不失一般性的情况下,笔者将电流输出设定为6个挡位,即0~5 A,其电流最大输出为5 A。
由自然频率计算公式和式(17)可知,电流与智能减振器的自然频率的关系为:
(18)
最后,经计算得到的智能减振器的刚度可在1 988 N/m~3 445 N/m范围内调节,智能减振器的自然频率可在41 Hz~54 Hz范围内调节。
在不同激励频率工况下,无减振器、普通减振器和智能减振器作用时,得到梁的振动加速度值如图10所示。其中,普通减振器即为没有控制系统的智能减振器,线圈中无电流。
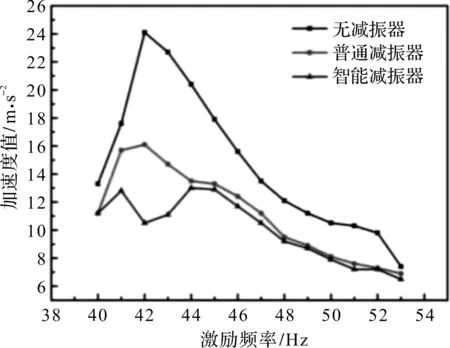
图10 智能减振器试验结果
由图10可知:智能减振器具有良好的减振性能,且减振效果明显优于普通减振器,尤其在简支梁达到共振时,智能减振器的减振效果尤为突出;
该智能减振器可调频带为14 Hz,具有较强的环境适应能力。在可调频带范围内,不同激励工况下,智能减振器都表现出良好的减振效果。
4.2 结果分析
笔者将式(18)计算的数据与试验得到的电流数据进行对比,以此来检测智能减振器控制系统的灵敏度,结果如表3所示。

表3 仿真数据与实验数据对比结果
由表3可知:仿真计算的结果与实验测试的结果趋势相同,但数据并不完全相符;对智能减振器系统及其试验结果进行分析,产生的误差主要由传感器的灵敏度、控制系统的稳定性及数据传递过程中存在的时间延迟所致。
5 结束语
针对现有参数可调式减振器的不足之处,笔者设计了一种新型的电磁弹簧结构,通过仿真优化了电磁弹簧的结构,确定了电磁弹簧模型;然后基于该弹簧模型,设计了一种刚度可调的智能减振器装置,并对智能减振器进行了仿真分析及实验验证;最后,测试了智能减振器刚度调节的灵敏性,对比了仿真数据,对误差进行了分析。
研究结果表明:
(1)电磁弹簧的整体刚度呈非线性,在平衡位置附近,刚度线性化程度较高;电磁弹簧的刚度与磁间距密切相关;
(2)电磁弹簧的磁间距尺寸应在10 mm~30 mm范围内,桶壁与振子之间的间距应在1 mm~2 mm范围内;
(3)智能减振器的减振效果明显优于普通减振器,在0~5 A的电流条件下,智能减振器的频率可调范围在14 Hz左右,具备宽频最优指标减振功能;
(4)在可接受的范围内,刚度调节存在一定的误差。
笔者设计的减振器具备智能、普通两种性能,在外激力工况变化不大时,可将该智能减振器控制系统关闭,并作为普通减振器使用,降低了电能的消耗。
在后续的研究工作中,笔者考虑将减振器结合实际的工程应用背景进行适配及推广,如管道振动减振、航天器微振动减振等;同时,在适配应用领域的同时,优化结构,选择轻量化的传感器,使其结构更小巧、紧凑,对被减振的物体影响更小。

