基于橡胶热氧老化规律的压缩机隔振脚垫动态特性研究

李 显， 陈俊杰,， 邱光琦， 杨超峰， 胡俊峰， 陈建军

(1.江西理工大学 机电工程学院，江西 赣州 341000;2.广东邦达实业有限公司，广东 中山 528455;3.安徽中鼎减震橡胶技术有限公司，安徽 宁国 242300)

橡胶隔振脚垫是空调器压缩机隔振系统的主要隔振元件，广泛应用于家用空调器、汽车空调器等。空调器压缩机工作时，家用空调外机(内含压缩机及橡胶隔振脚垫)的内部温度最高可达108 ℃，橡胶隔振脚垫在外界温度影响下会产生热氧老化现象，热氧老化后橡胶的刚度及阻尼不断变化，导致橡胶隔振脚垫动态特性随热氧老化程度的变化而不断改变，使得空调器压缩机及管路的振动、噪声逐渐增大，甚至损坏空调管路。因此，建立考虑热氧老化因素的橡胶隔振脚垫动态特性模型对预测服役后的家用或工业用空调器的振动情况具有较重要的理论和工程意义。

橡胶隔振脚垫静刚度分析求解是研究动刚度[1]的基础，小变形情况下常用Mooney-Rivlin本构模型[2-5]，Kaya等[6]对橡胶的超弹性进行建模分析与形状优化，通过单轴拉伸与平面拉伸等试验，运用材料本构模型进行数值拟合得到模型参数。何小静等[7]对橡胶试片单轴拉伸、等双轴拉伸和平面剪切进行试验，拟合了常用的6种本构模型的材料参数，为不同工程应用情况下选择合适的本构模型提供了有益参考，但未对其动态特性进行研究。

Loh等[8]建立了空调器压缩机-管路有限元模型，利用MTS830弹性体试验台对橡胶隔振脚垫的径向和轴向静、动刚度进行测试，给出了橡胶隔振脚垫的刚度特性预测方法。但其动刚度测试工况仅有25 Hz、47 Hz两个频率点，测试数据不够且未建立相关数学模型。经典的Kelvin-Voigt模型、Maxwell模型、三元件固体模型以及由多种基本元件组合成其他模型常用于表征橡胶隔振器动态特性的频率相关性[9-10]。吴杰等[11]用超弹性模型、若干广义Maxwell模型和若干理想弹塑性模型并联相叠加，通过剪切试验对模型参数进行识别，有效表征振幅相关性和频率相关性。但该模型所含参数较多，试验量较大，实际工程应用时效性不足，若仅用一个上述经典模型，则拟合精度不足。陈俊杰等[12-13]引入分数导数模型和库仑摩擦模型对空气弹簧橡胶气囊进行建模，试验值与理论值取得了良好的一致性。但未考虑热氧老化等因素对其刚度及阻尼影响，未对热氧老化后的动态特性进一步深入研究。

以上橡胶隔振设计的动态特性分析多应用于汽车隔振领域，对于空调器压缩机橡胶隔振脚垫的动态特性研究分析较少，且大多未考虑热氧老化因素对橡胶隔振元件动态特性影响[14]。Azura等[15]从材料级别研究了不同炭黑种类及填充量对天然橡胶的力学、导电、老化等性能影响，并在100 ℃加速老化试验下探究老化对其力学性能影响，但仅考虑炭黑影响不足以反映老化对其黏性力影响。Rodas等[16]通过热-力完全耦合的方法建立热-超弹-黏弹耦合模型，预测了橡胶在低周疲劳条件下的橡胶拉伸试样的生热状态，并讨论了应变率及最大应变载荷对橡胶结构件生热的影响，但未考虑生热后橡胶不断老化的力-位移关系变化。

为弥补上述研究中的不足，文中考虑热氧老化对橡胶隔振脚垫的动态力学特性影响，基于热氧加速老化[17]试验，引入Arrhenius模型[18]对橡胶隔振脚垫动态特性模型进行改进；提出采用Arrhenius模型、分数导数Kelvin-Voigt模型和库仑摩擦模型，建立压缩机橡胶隔振脚垫热氧老化-动态特性数学模型,给出该模型参数的识别方法，进一步完善计及老化因子的橡胶隔振脚垫动态特性模型。通过理论及试验对热氧老化前、后的橡胶隔振脚垫动态特性进行了分析，为橡胶隔振脚垫的刚度匹配及优化奠定基础。

1 隔振脚垫热氧老化-动态特性建模

包含橡胶隔振脚垫的空调器压缩机系统如图1所示，外部环境温度及压缩机运转产生的热量使橡胶隔振脚垫所处的环境温度不断升高，长期工作于这种温度环境的隔振脚垫动态力学性能因热氧老化产生退化，故需要引入热氧老化相关模型对其动态特性进行修正，从而更为精确地描述其动态特性的演化机理。

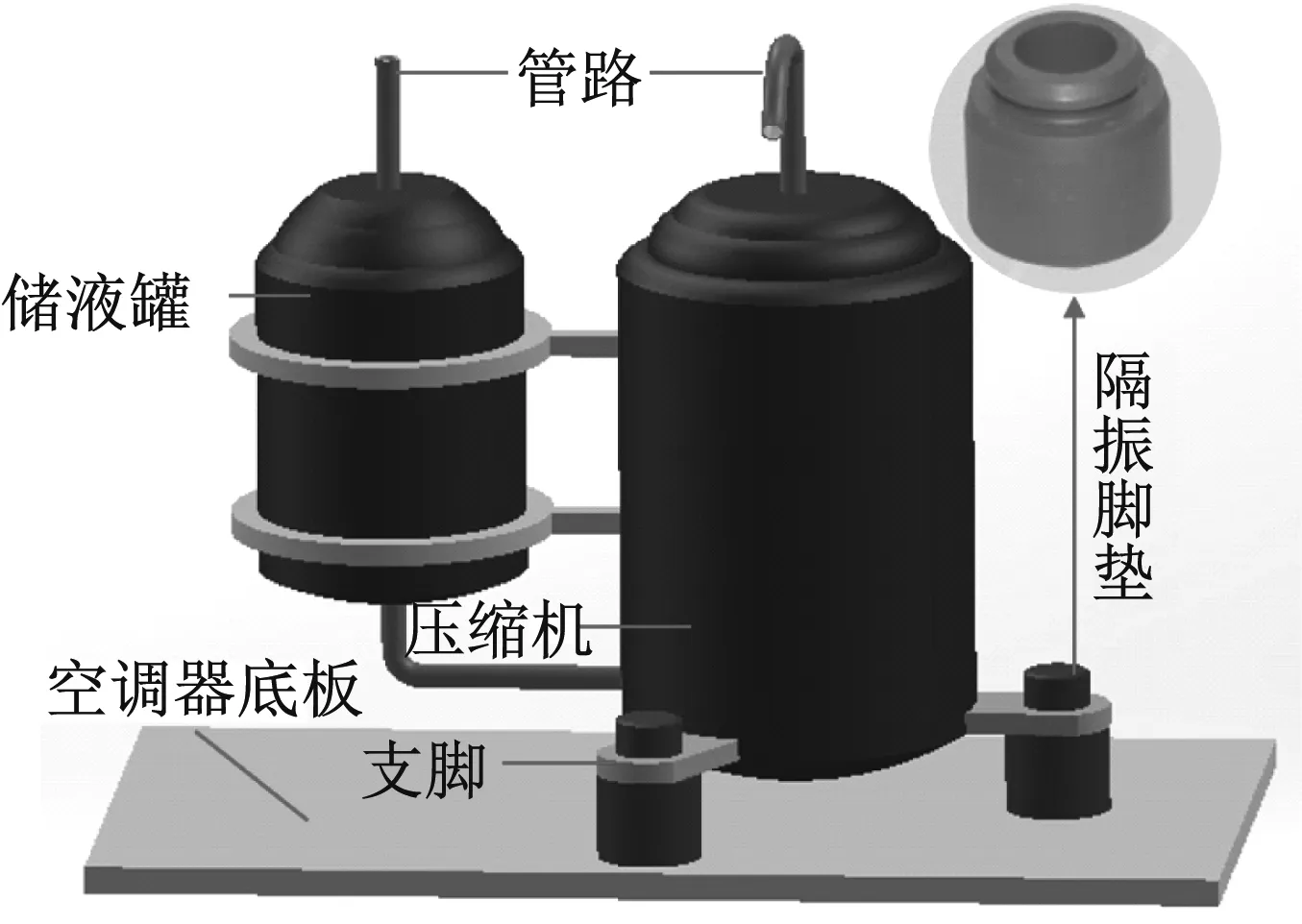
图1 压缩机与橡胶隔振脚垫Fig.1 Compressor and rubber vibration isolation pads

橡胶热氧老化的评估及性能退化行为常用Arrhenius行为进行描述，Arrhenius方程式为

(1)

式中:A(T)为反应速率;C1为耐热氧老化相关的加速系数;Ea为活化能;R为摩尔气体常数;T为热力学温度。基于Arrhenius方程，橡胶隔振脚垫的热氧老化变量表达式为

(2)

式中:μ为热氧老化因子;t为热氧老化时间。建立橡胶隔振脚垫的动态特性模型时，也必须考虑其频率相关性和振幅相关性。如图2所示，本文建立了考虑热氧老化因子的基于分数导数Kelvin-Voigt模型和库仑摩擦模型的橡胶隔振脚垫动态模型。

线弹性模型用于描述橡胶隔振脚垫的线性力与位移关系；分数导数标准模型用于描述橡胶隔振脚垫频率相关性；线弹性模型与分数导数模型并联组成分数导数Kelvin-Voigt模型；库仑摩擦模型用于描述橡胶隔振脚垫振幅相关性；基于Arrhenius模型的热氧老化因子μ，描述橡胶隔振脚垫的热氧老化相关性。

热氧老化前，橡胶隔振脚垫线弹性模型力与位移关系式为

Fke=Kex

(3)

式中，Ke为线弹性刚度。橡胶隔振脚垫分数导数标准模型黏性力与位移关系为

Fkv=bDαx

(4)

式中:α为分数导数阶次;b为分数导数阻尼参数;Dα表示分数阶微分形式。由弹性模型与分数导数模型并联而成的分数导数Kelvin-Voigt模型力与位移关系式为

Fv0=(Ke+bDα)x

(5)

对式(5)进行傅里叶变换可得分数导数Kelvin-Voigt模型橡胶隔振脚垫动刚度、损耗角为

(6)

(7)

碳黑填充橡胶的振幅相关性类似摩擦关系，采用库仑摩擦模型描述其振幅相关性，库仑摩擦力Ff与位移x的关系为

(8)

式中:(Ffs，xs)为力与位移关系曲线上的状态参考点，初始取值为(0，0)；ε=Ffs/Ffmax。最大摩擦力Ffmax和达到最大摩擦力一半时所对应的位移x2，三者参数关系式为

(9)

式中，Kmax为迟滞回线两端位移处的最大斜率。库仑摩擦模型的刚度Kf、能量损失Ef和损耗角δ1为

(10)

(11)

(12)

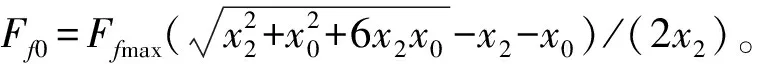
Kvf=Kfcosδ1+Kvcosδ0+j[Kfsinδ1+Kvsinδ0]

(13)

(14)

(15)

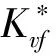
考虑热氧老化相关性，引入热氧老化因子μ，则计及热氧老化因子的线弹性模型力与位移关系为

Fkea=μKex

(16)

为更准确地描述橡胶热氧老化下黏弹性力变化情况，文献[19]引入了多个材料参数进行优化控制，但参数较多，识别较为困难。为简化参数以及准确表征热氧老化下橡胶隔振脚垫的黏弹性变化规律，文中仅引入线性参数β，则分数导数模型力与位移关系式为

Fkva=βμbDαx

(17)

故计及热氧老化因子的分数导数Kelvin-Voigt模型力与位移关系式为

Fva=μ(Ke+βbDα)x

(18)

对式(18)进行傅里叶变换可得分数导数Kelvin-Voigt模型橡胶隔振脚垫动刚度、损耗角为

(19)

(20)

同理，计及热氧老化因子的库仑摩擦模型力与位移关系为

(21)

相应库仑摩擦模型的刚度Kfa、能量损失Efa和损耗角δa1为

Kfa=μKf

(22)

Efa=μEf

(23)

(24)

从而得到橡胶隔振脚垫热氧老化后复刚度、动刚度及损耗因子为

Kvfa=Kfacosδa1+Kvacosδa0+j[Kfasinδa1+Kvasinδa0]

(25)

(26)

(27)

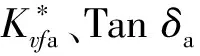
图2中:Ke、Kv与Kf分别为线弹性刚度、分数导数Kelvin-Voigt模型刚度与库仑摩擦模型刚度;μ、β分别为热氧老化因子与材料参数;Fke、Fkv与Ff分别为线弹性力、黏弹性力与库仑摩擦力;F、x分别为合力、位移激励。

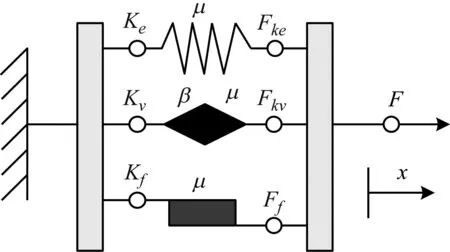
图2 隔振脚垫热氧老化-动态特性模型Fig.2 Thermal oxygen aging-Dynamic characteristic model of rubber vibration isolation pads

2 试验装置与试验方法

文中试验装置由MTS831弹性体试验台、橡胶隔振脚垫(合作企业生产，以三元乙丙橡胶为主要原料，其结构及相关外形尺寸如图3所示)、GDS-250高低温湿热试验箱、工装等组成。

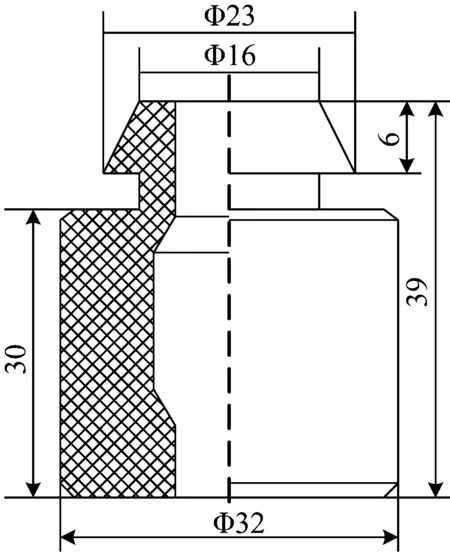
图3 橡胶隔振脚垫结构示意图(mm)Fig.3 Schematic diagram of rubber vibration isolation pad structure(mm)

试验方法如下：

(1) 橡胶隔振脚垫的热氧老化温度T设置为100 ℃，热氧老化过程严格按照ISO 188—2011《Rubber, vulcanized or thermoplastic—Accelerated aging and heat resistance tests》[20]实施。参考标准JIS K6386—1999《Rubber materials for vibration isolators》[21]，同时根据实际工程应用，将橡胶隔振脚垫热氧老化后邵氏硬度H变化值为5度作为加速热氧老化临界点。选取同一批硫化制造且硬度为31度的30个橡胶隔振脚垫，留下2个热氧老化前的橡胶隔振脚垫，将剩下28个橡胶隔振脚垫放入试验箱。每隔24小时拿出2个橡胶隔振脚垫，常温静置24小时后用邵氏硬度计进行测试，硬度测试按照ISO 7619-1:2010《Rubber, vulcanized or thermoplastic—Determination of indentation hardness-Part 1: Durometer method(Shore hardness)》[22]执行，直至硬度变化5度时停止试验，硬度随热氧老化时间t的增加而变化的测试结果如表1所示。

表1 不同热氧老化时间下硬度数据

(2) 橡胶隔振脚垫的静、动态力学性能测试在MTS831弹性体试验台进行，由于30个橡胶隔振脚垫为同批生产，在相同热氧老化条件下，各橡胶隔振脚垫之间的差异性较小，可忽略不计，故热氧老化前后各取1个橡胶隔振脚垫测试。将热氧老化前留下的2个橡胶隔振脚垫取其中1个编为1号，热氧老化后硬度刚好变化5度的橡胶隔振脚垫取其中1个编为2号，制作相应的工装，试验装置如图4所示。试验测试时，根据压缩机的重量分配，施加37 N的预载。并在作动端施加速度为10 mm/min，振幅分别为0.3 mm、0.5 mm、1 mm三角波信号测试其静刚度特性；作动端施加振幅分别为0.05 mm、0.3 mm、0.5 mm，频率范围为2～100 Hz，间隔2 Hz的正弦扫频信号测试其动刚度特性。

图4 静、动态特性试验装置Fig.4 Test rig of static characteristics and dynamic characteristics

3 参数识别及模型验证

3.1 参数识别

在100 ℃的热氧老化中，橡胶隔振脚垫被认为是均匀老化，其老化机理一致，即反应的活化能Ea保持不变，Ea具体识别方法见参考文献[23]。其中，R、T为常数，根据试验曲线采用图4方法所得老化前、后的Ke值可计算出热氧老化7天后的老化因子μ7；再依据式(2)与式(19)可以得到加速系数C1和材料参数β，各参数如表2所示。

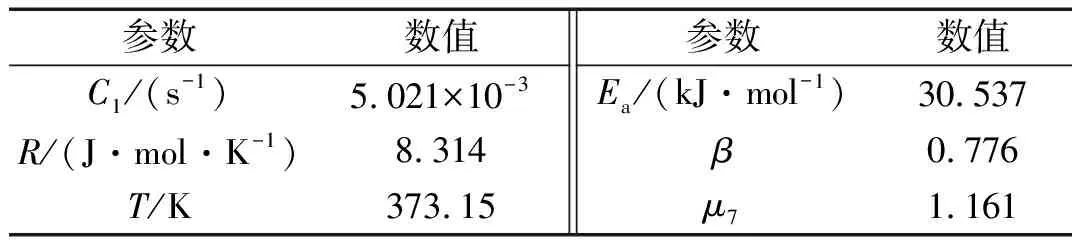
表2 Arrhenius模型相关参数

为尽量减小橡胶隔振脚垫黏性力的影响，静刚度实验时需尽量降低加载频率，使库仑摩擦力起主要贡献。静刚度测试时，MTS831弹性体试验台其液压作动器对橡胶隔振脚垫施加一个加载速度为10 mm/min，振幅为1 mm的三角波激励信号。如图5所示，根据试验获得的迟滞回线可识别出橡胶隔振脚垫模型中的Ke、Ffmax与Kmax，橡胶隔振脚垫静刚度取决于线弹性模型和库仑摩擦模型，库仑摩擦模型的参数识别方法详见文献[24]，橡胶隔振脚垫热氧老化前后静刚度的试验值与计算值所得迟滞回线如图6所示。

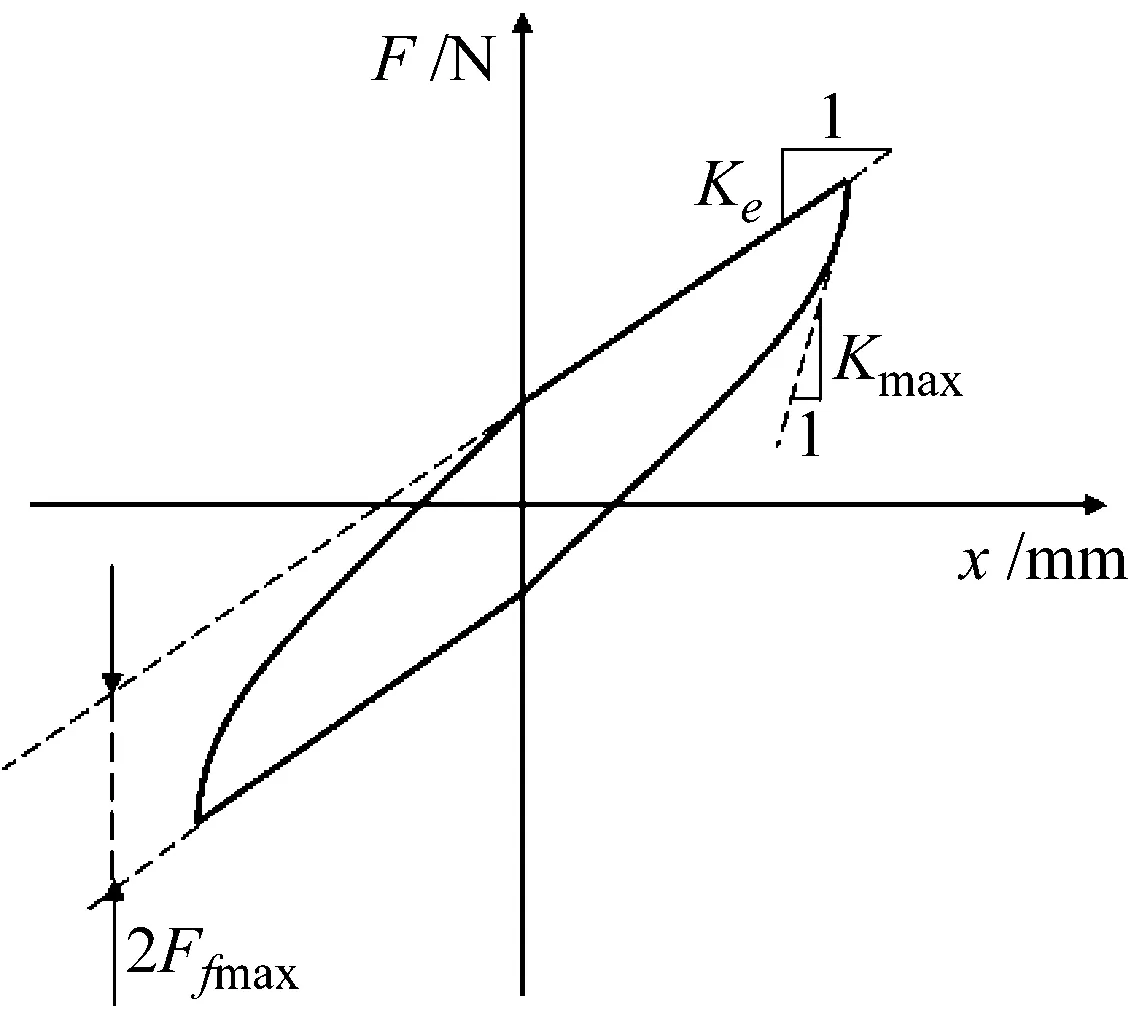
图5 库仑摩擦模型参数识别Fig.5 Parameter identification of smooth Coulomb friction model

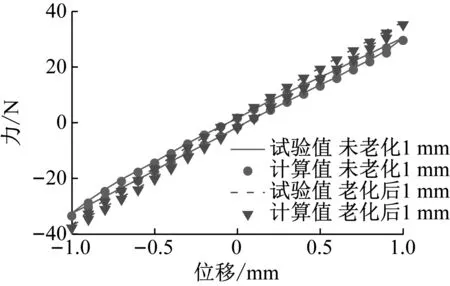
图6 热氧老化前后迟滞回线(振幅1 mm)

由图6可见，热氧老化后橡胶隔振脚垫的迟滞回线向上倾斜，热氧老化7天后静刚度增加19.35%。从橡胶隔振脚垫热氧老化前后迟滞回线的试验值与计算值来看，两者吻合较好，计算值与试验值相对误差小于3.3%。

橡胶隔振脚垫动刚度试验时，为尽量减小库仑摩擦力的影响，需尽量采用低振幅信号进行试验。故MTS831液压作动器施加的激励信号采用振幅为0.05 mm，频率范围为2～100 Hz，间隔2 Hz的正弦扫频信号可得到分数导数Kelvin-Voigt模型在该激励信号下对单个橡胶隔振脚垫动刚度特性的贡献值，采用最小二乘法拟合得到分数导数阶次α和阻尼参数b，辨识得到热氧老化前隔振脚垫动态特性模型参数如表3所示。

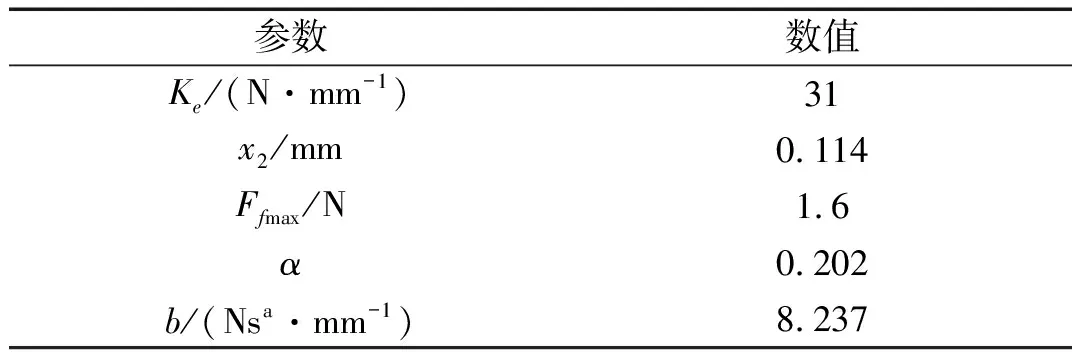
表3 橡胶隔振脚垫动态特性模型参数

可得橡胶隔振脚垫振幅为0.05 mm时，其动刚度和损耗因子计算、试验曲线如图7所示。

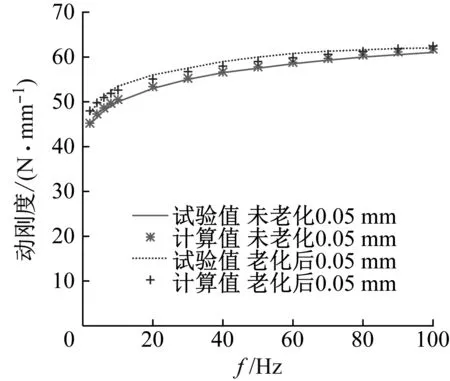
(a) 动刚度

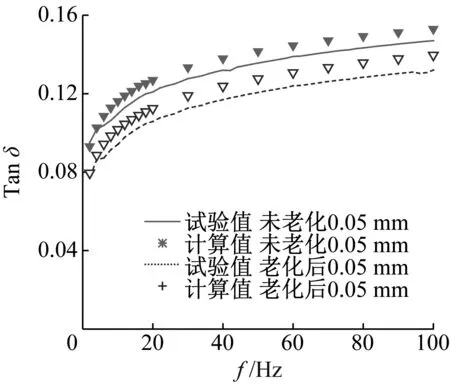
(b) 损耗因子图7 热氧老化前后动刚度与损耗因子(振幅0.05 mm)

由图7可见，尽管热氧老化前、后橡胶隔振脚垫的动刚度及损耗因子都随频率增加呈不断增加的趋势；但热氧老化7天后动刚度较热氧老化前最大增长5.3%，而损耗因子较热氧老化前最大减小11.6%。从热氧老化前后动刚度的试验值与计算值来看，计算值与试验值的相对误差均小于5%，热氧老化前后损耗因子的计算值与试验值相对误差均小于7.5%，表明所辨识参数的正确性与有效性。

3.2 模型验证

当加载速度为10 mm/min，采用振幅为0.3 mm、0.5 mm的正弦激励信号时，橡胶隔振脚垫热氧老化前后的静刚度迟滞回线如图8所示。由图8可知，虽然模型参数是从振幅为1 mm时试验曲线所识别，但所识别的参数可较准确的复现振幅为0.3 mm、0.5 mm时的迟滞特性，故文中所建立的热氧老化-动态特性模型可准确表征橡胶隔振脚垫热氧老化前后在不同振幅下的迟滞特性，且在不同振幅下热氧老化后橡胶隔振脚垫的静刚度皆明显增大，表明考虑橡胶隔振脚垫的热氧老化相关性至关重要。

为验证热氧老化对橡胶隔振脚垫振幅相关性及频率相关性的影响，采用振幅为0.3 mm、0.5 mm，频率范围为2～100 Hz，间隔2 Hz的正弦激励对热氧老化前后的橡胶隔振脚垫进行扫频测试，其热氧老化前后动刚度和损耗因子计算、试验曲线如图9所示。由图9可见，橡胶隔振脚垫在振幅为0.05 mm时所识别的模型参数同样可以很好的复现振幅为0.3 mm、0.5 mm时的动刚度特性与损耗因子，表明热氧老化-动态特性模型能够准确地描述橡胶隔振脚垫热氧老化前后的动刚度与损耗因子变化规律，进一步验证了模型的正确性。在不同振幅下橡胶隔振脚垫热老化后的损耗因子较热氧老化前皆呈减小趋势，橡胶隔振脚垫的减振性能衰退；且热氧老化后刚度增大，使得橡胶隔振脚垫的隔振效果变差，导致压缩机的振动加剧，噪声增大。

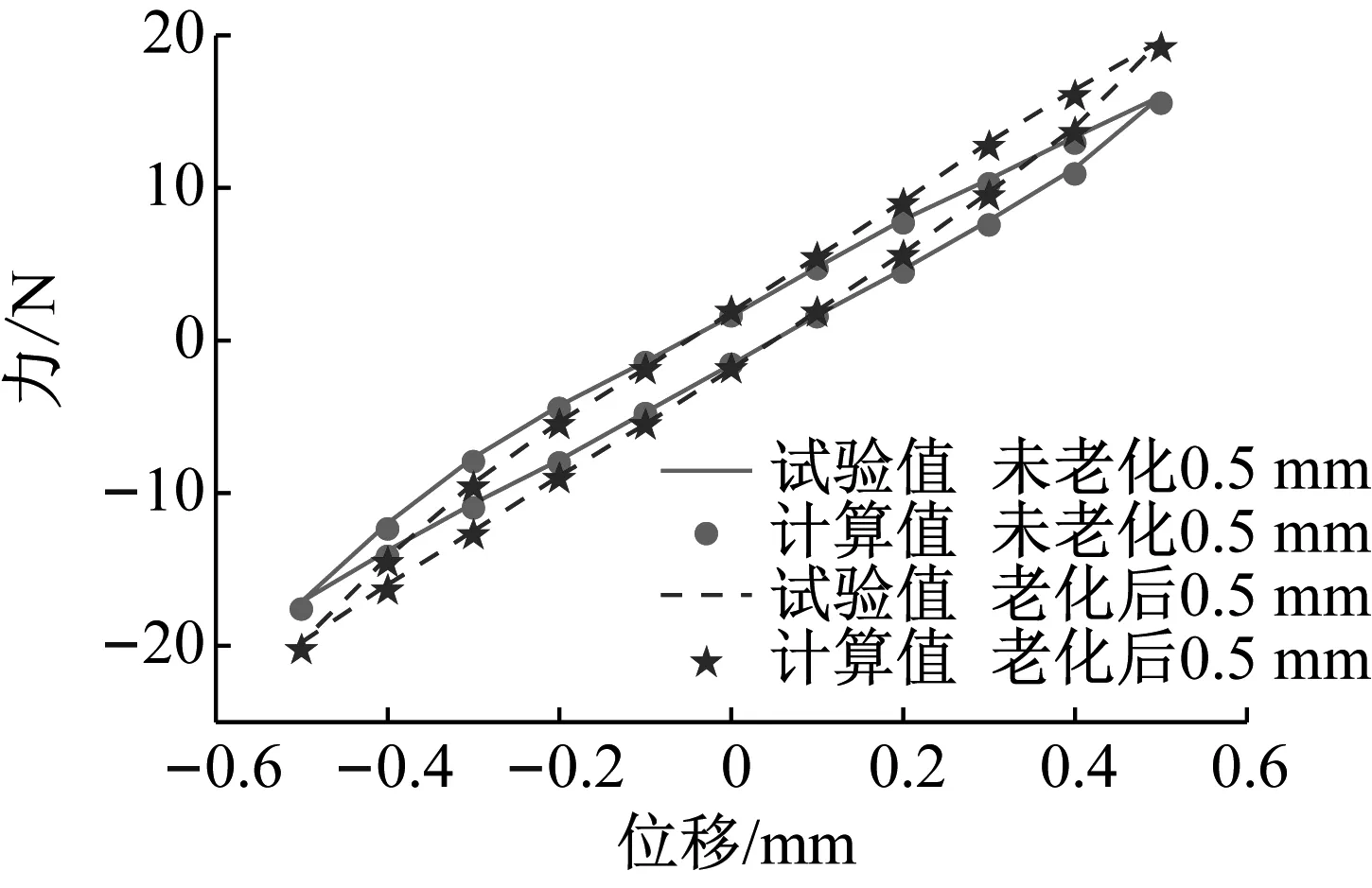
(a) 振幅0.5 mm

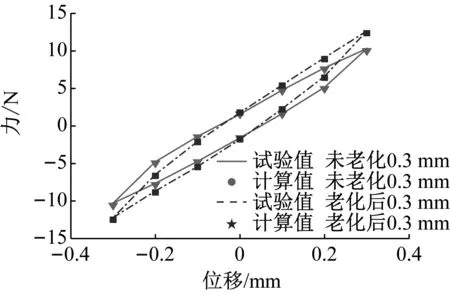
(b) 振幅0.3 mm图8 不同振幅下迟滞回线Fig.8 Hysteresis loop under different amplitudes

本文研究的橡胶隔振脚垫在热氧环境及硫化体系共同作用下发生侧基氧化反应，内部分子链会进一步交联[25]，交联密度增大，形成了性能更为稳定的C-C交联键，导致橡胶交联硬化；橡胶隔振脚垫配方中的防老体系在高温热氧状态下捕捉环境中的游离氧和橡胶自由基并与之结合，降低了橡胶分子的降解速度，使得橡胶隔振脚垫的老化以交联为主；热氧环境下橡胶交联硬化与其降解速度降低的综合作用导致了橡胶隔振脚垫静刚度增大[26-30]。结合式(6)、(13)、(19)和(25)可知，动刚度将随静刚度的增大而增大。

本文所建模型可预测隔振脚垫在热氧环境中的动态特性变化，为隔振脚垫的刚度匹配及优化提供了理论基础。在隔振脚垫与压缩机匹配最优时，热氧条件下静刚度的变化破坏了隔振脚垫与压缩机性能匹配的合理性[31]，导致隔振脚垫的隔振效果变差。因此，可适当调整隔振脚垫设计的初始刚度；使其在性能可接受的范围内将隔振脚垫的刚度值设计为小于最优匹配刚度值，则隔振脚垫在热氧老化一定时间后将达到最优匹配刚度，间接延长了隔振脚垫使用寿命，优化了隔振脚垫的性能匹配设计。

(a) 动刚度(振幅0.5 mm)

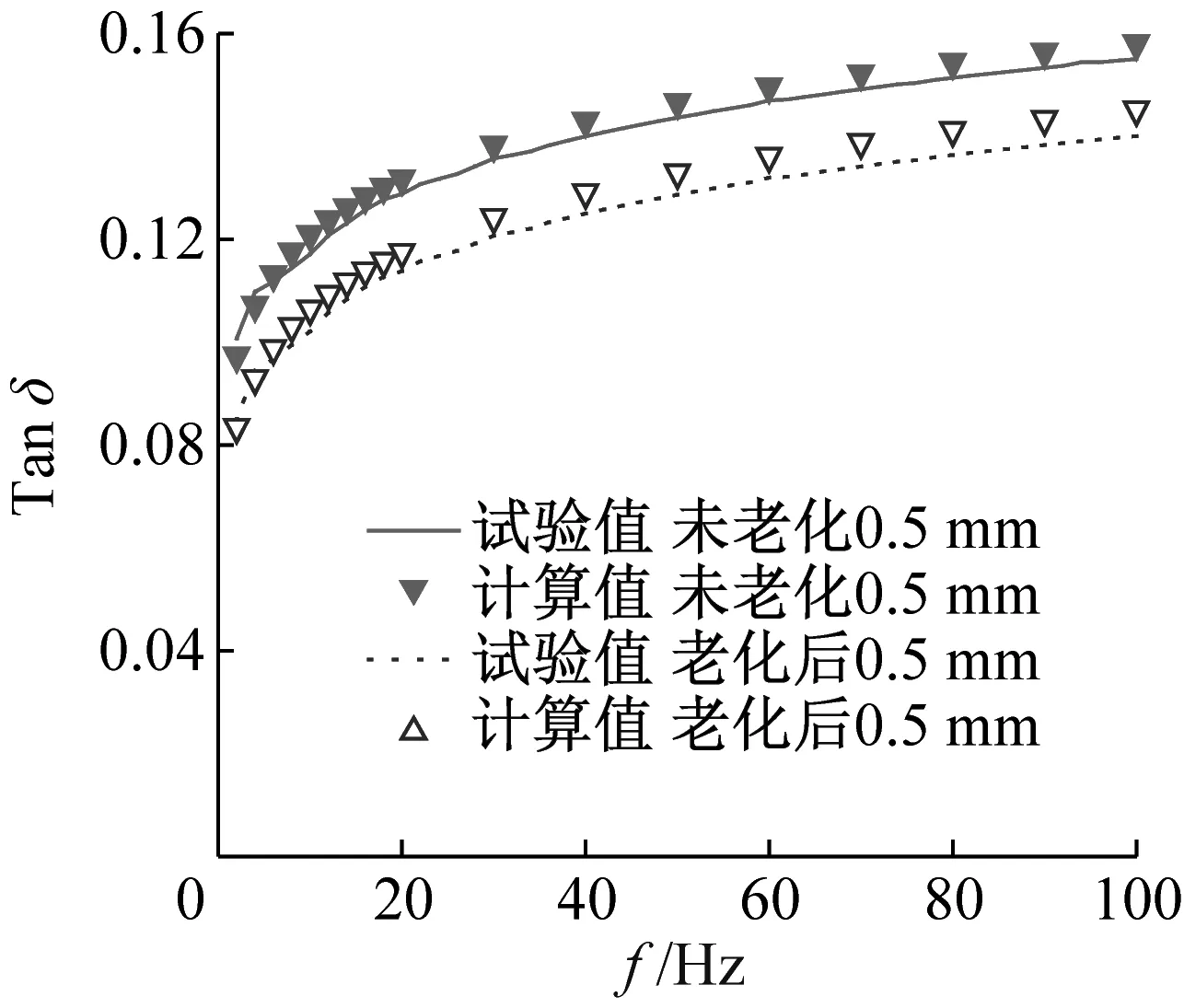
(b) 损耗因子(振幅0.5 mm)

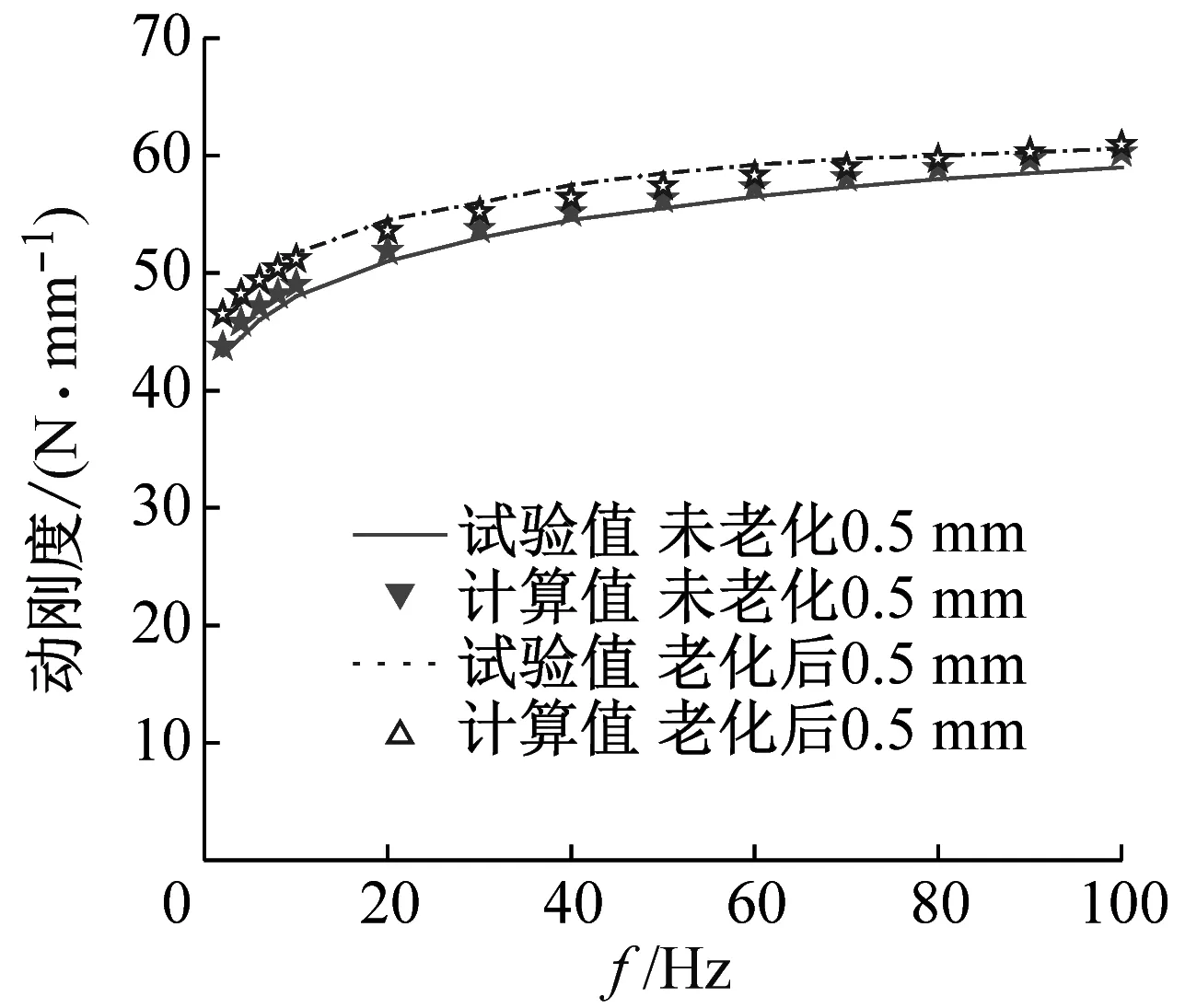
(c) 动刚度(振幅0.3 mm)

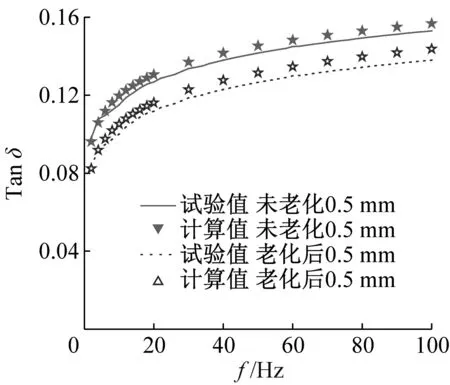
(d) 损耗因子(振幅0.3 mm)图9 不同振幅下橡胶隔振脚垫动刚度及损耗因子

4 结 论

(1) 文中引入Arrhenius模型、分数导数Kelvin-Voigt模型、库仑摩擦模型，建立了橡胶隔振脚垫热氧老化-动态特性数学模型，给出了该模型参数的识别方法，进一步完善了橡胶隔振脚垫的动态特性建模方法。

(2) 通过热氧加速老化、隔振脚垫静、动态特性试验，辨识了模型参数，并基于不同振幅、频率的静、动态加载试验进行模型验证，结果表明所建立热氧老化-动态特性模型老化前、后静刚度的计算值与试验值相对误差小于3.3%，动刚度的计算值与试验值相对误差小于5%，损耗因子的计算值与试验值相对误差小于7.5%，表明所建立模型可准确描述橡胶隔振脚垫的迟滞回线特性、振幅相关性、频率相关性和热氧老化相关性，验证了该模型的准确性。

(3) 橡胶隔振脚垫热氧老化后由于橡胶分子链交联密度变化，相比热氧老化前，其静刚度增长19.35%、动刚度最大增长5.3%、损耗因子最大减小11.6%。文中所建立的模型能够很好地描述热氧老化对橡胶隔振脚垫刚度、阻尼特性变化规律，为深入研究外界环境温度因素导致橡胶热氧老化的隔振脚垫服役后动态特性演化规律提供基础。