基于有效含水量的土壤水分监测点布设的空间分层采样方法

金建华，张宝忠，刘 钰，毛晓敏

基于有效含水量的土壤水分监测点布设的空间分层采样方法

金建华1,2,3，张宝忠1,4※，刘 钰1,4，毛晓敏2

（1. 中国水利水电科学研究院流域水循环模拟与调控国家重点实验室，北京 100038； 2. 中国农业大学水利与土木工程学院，北京 100083； 3. 天津农学院水利工程学院，天津 300384； 4. 国家节水灌溉北京工程技术研究中心，北京 100048）

为了优化灌溉实践，构建准确估计平均土壤水分的监测点布设准则，该研究引入有效含水量（Available Water Capacity, AWC）作为辅助变量，结合经典统计学和地统计学构建了一种基于辅助变量空间自相关的分层采样方法（Stratified Sampling method based on spatial autocorrelation of Auxiliary Variables，SSAV），克服直接以土壤水分为变量时受其强时空变异影响的弊端，并在田块尺度进行试验。结果表明：0～40和0～80 cm土层的AWC服从正态分布；在90%置信区间，采样误差为10%时研究区内0～40和0～80 cm土层的监测点数目分别为7个和6个；基于SSAV布点法估计土壤水分的相对误差变化范围为–23.23%～35.15%，较简单随机布点（Simple Random Sampling，SRS）法减小了26.48%。标准差的平均值为4.78%，较SRS降低了17.30%。基于SSAV的0～40和0～80 cm 2个土层的估计值和观测值之间的平均均方根误差RMSE为0.010 4 cm3/cm3，基于SRS的RMSE为0.012 0 cm3/cm3，显著性检验<0.001，SSAV显著提高了对土壤水分的估计精度和准度。SSAV为获得区域平均土壤水分提供了省时、省力、低成本的监测点布设方案，为农业水资源管理和提升农业用水效率提供了保障。

土壤；水分；采样；地统计学；有效含水量；空间相关性；空间变异性

0 引 言

土壤水分是水文、生态、环境过程和农业过程中的主导因素之一[1-2]，其空间分布在水文、农业和气候模拟与预测中具有重要应用[3]。尤其在干旱和半干旱地区，平均土壤水分是地面灌溉条件下大田作物决定灌溉管理决策的关键指标。然而，目前尚无准确可靠的土壤水分的监测方法，因此近年来土壤水分监测成为研究热点[4]。许多学者认为土壤水分具有很强的时空变异性[5]，准确地估计土壤水分需要大量的高频率采样，因此，合理、经济、高效的采样策略成为解决问题的关键[6]。

土壤水分采样策略的关键在于监测点的数量和位置。目前土壤水分监测点布置方法主要包括传统统计特征采样法、地统计采样法和基于先验知识的分层采样法。基于传统统计的采样方法主要包括简单随机采样（Simple Random Sampling，SRS）和规则采样，传统统计采样方法基于“空间变量随机分布”这一前提，监测点的数目仅与样本的变异系数的平方有关[6-7]。Brocca等[8- 9]利用该方法确定了监测点的布设数量。事实上土壤水分变化并非完全随机，在不同尺度上土壤水分均呈现出一定的空间结构[5,10]，具有明显的空间相关性[11]。Wang等[12]发现土壤水分在干旱条件下变程较大，湿润条件较小。当监测点间距离小于空间相关范围时，不满足空间变量随机分布这一前提条件，所得出的合理取样数目便不能完全代表土壤水分的实际信息，因此传统统计采样具有一定的缺陷。

地统计采样法考虑了变量的空间结构和变异，克服了样本独立的缺陷[13-14]，尤冬梅[15]利用地统计方法研究了农田土壤重金属污染监测及空间估值。赵倩倩等[16]将地统计学与GIS相结合，对县域土壤养分空间变异特征及合理监测点数进行了研究。但是，地统计采样法以半方差函数和克里格插值为基本工具[16]，而半方差函数的确定需要事先进行大量的土壤取样以获取土壤信息。如果不具备丰富的先验知识，则难以利用地统计学进行采样设计[17]。因此基于地统计法的采样在实际应用中存在一定的困难[6]。

分层采样是目前较为精确的抽样方法之一。近年来分层采样被广泛应用于土壤属性调查与监测[18]、作物种植面积估算[19-20]、农业统计等方面。相关研究还指出分层的关键在于，应使层内方差尽量小，层间方差尽量 大[21]，以提高对目标变量的估计精度。具有空间相关性的地理对象的分层抽样估计精度取决于先验知识的空间相关性特征和丰富程度[22]。

有效含水量（Available Water Content，AWC）是指介于田间持水量和凋萎含水量之间的能被植物吸收利用的土壤水分，与植被恢复和作物生长关系密切，是土壤的固有属性，反映了土壤对植物的供水能力。AWC主要与土壤特性有关，空间分布模式较土壤水分稳定。此外，AWC与土壤水分均受土壤质地、地形、植被覆盖等因素的影响，二者在时空分布上具有较强的相关性。高晓东等[23-24]发现AWC和土壤水分具有相似的时间变异趋势和很强的空间相关性。然而，目前AWC没有被引入作为辅助变量研究土壤水分监测点的布设。因此若考虑引入AWC为先验知识，辅助土壤水分监测点的布设，则有助于克服直接以土壤水分为变量时受其强时空变异性影响的弊端。

基于以上分析，本文提出构建一种以AWC为辅助变量，结合经典统计法、地统计学方法的分层采样的土壤水分监测点优化布设方法（Stratified Sampling method based on spatial autocorrelation of Auxiliary Variables，SSAV），以降低采样成本，提高监测点的代表性和对土壤水分估计的精度，提高农业用水效率。

1 材料与方法

1.1 研究区概况

本试验在国家节水灌溉北京工程技术研究中心大兴试验基地（N39°37.25'，E116°25.51'）周边开展。研究区地处北京南部，属于永定河冲积平原，海拔在15～45 m间，地形平坦。研究区气候属于暖温带半湿润大陆性季风气候，冬春季寒冷干燥，夏秋季温暖湿润，雨热同期，年均气温为11.6℃，年均降水量556.4 mm，降水年内分布不均，多集中在7–9月份。土壤类型为潮土。

1.2 试验设计

试验区面积为3.645 km2，南北长2 700 m，东西宽 1 350 m，采用格网法布设取样点，格网大小为150 m×150 m，共162个，借助GPS记录采样点坐标。供试作物为夏玉米，每年6月上旬播种，9月下旬收获。每个生育期的起止时间为每年的6月上旬至9月下旬，并于每个生育期内的拔节（7月中旬—8月上旬）、灌浆（8月下旬—9月上旬）、成熟（9月中旬—9月下旬）阶段各测定一次土壤水分。2016—2018年，3个生育期内，共测土壤水分9次，每次所测研究区土壤含水率的最大值、最小值、均值如图1所示。

1.3 数据收集

0～80 cm为玉米根系的主要分布区和耗水区域，所以测定深度确定为0～80cm，土壤分层取样，每20 cm一层，共分为4层（0～20、＞20～40、＞40～60、＞60～80 cm）。0～40 cm代表耕作层，苗期根系分布在0～40 cm土层中，开花和蜡熟期在0～40 cm土层根系分别占总根量的80%和55%左右，即在垂直方向上玉米的主体根系分布在0～40 cm土层中。0～40 cm土层受人类活动和根系分布等影响剧烈，土壤水分和AWC空间变异程度较0～80 cm土层高，因此两土层的监测点数量不同；同时，土壤水分和AWC的空间分布也存在差异。因此本文分0～40、0～80 cm 2个土层考虑监测点的布设。

对于每个取样点，采集原状和扰动土壤样品以测定土壤水分、土壤容重、田间持水量和土壤水分特征曲线。田间持水量采用wilcox[25]法测定；土壤水分特征曲线采用离心机（Hitachi CR22GIII，日立，日本）法测定（压力为0.1，0.3，0.5，0.7，1，2，3，5，9，12和15bar）；凋萎点含水量通过土壤水分特征曲线获得，凋萎系数为一个常数[24-25]，对应的土壤水势为–1 500 kPa；土壤质量含水率通过土钻取土，用烘箱在105℃条件下烘8～12 h确定，然后通过土壤容重换算为体积含水率。

1.4 基于土壤最大有效含水量的空间分层采样

1.4.1 AWC

本文采用AWC作为辅助参量，用于确定土壤水分监测点的布设数量和位置，其计算公式如下：

AWC=FC–PWP （1）

式中AWC为土壤有效含水量，cm3/cm3；FC为田间持水量，cm3/cm3；PWP为永久萎蔫系数，cm3/cm3。

1.4.2 监测点布设数量的确定

很多学者采用传统统计法确定监测点的数量[26-27]，当采样点的AWC相互独立且服从正态分布时，具体计算公式如下：

（2）

变异系数CV的计算公式如下：

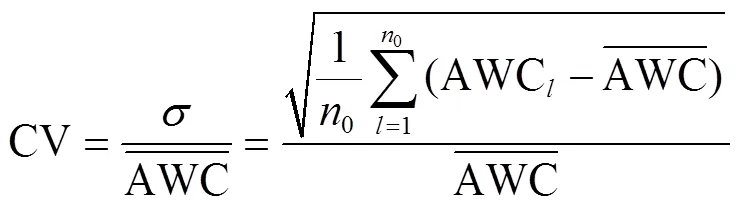
（4）

1.4.3 AWC的空间变异分析

本文采用地统计学中的半方差函数分析AWC的空间相关性。计算公式如下：

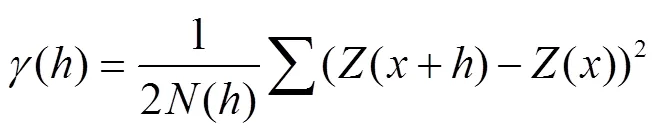
式中()为变量间距为的半方差，此处为AWC；()和(+)坐标为和+处的AWC；()为被距离相隔的试验样本点的对数。

常见的理论变异函数模型分别是球形模型、指数模型、高斯模型，本文中使用的模型有指数模型和高斯模型。变程是半方差函数中的重要参数，代表了变量的空间自相关范围，可以通过地统计学软件求得。本文利用变程辅助确定监测点的位置。

1.4.4 监测点布设位置确定及土壤水分估计

土壤水分监测点位置的确定分0～40和0～80 cm 2个土层进行考虑。2个土层所需的监测点数量按公式（2）计算。

1）简单随机采样（SRS）

在研究区域内随机抽取个监测点。基于采样点的实测土壤水分值利用普通克里格插值绘制土壤水分等值线图，利用土壤水分等值线图确定个监测点的土壤水分。个监测点的土壤水分的均值作为土壤水分的估计值。

2）基于AWC的空间相关性的分层采样（SSAV）

根据研究区域实测的AWC数值及取样点的坐标，利用克里格空间插值获得研究区AWC的空间分布图。为了保证空间分布图的可靠性，取样点采用格网法布设，以保证取样点对研究区覆盖的均匀性和完整性。将取样点实测的AWC值从小到大排列，根据取样点数等分的原则划分为段，且根据每段的数值范围将研究土层划分为层。在本文中取因此每层布置1个监测点，要求任意2个监测点间的距离大于该土层AWC的变程，以确保监测点间相互独立。基于采样点的实测土壤水分利用普通克里格插值绘制实测土壤水分空间分布图，利用土壤水分等值线图确定个监测点的土壤水分。

Manly[29]建议自助采样实际应用中的重复采样次数应不少于1 000次。抽样次数的增加有助于更好地反应监测点布设方法的稳定性。为了分析SRS和SSAV两种采样方法估计土壤水分的效果，提高结果的代表性并降低抽样误差影响，本文确定抽样次数为10 000次，每种监测点布设方法均进行10 000次抽样，最终获得10 000组监测点。

1.5 土壤水分监测结果的评价指标

本文中利用均方根误差（RMSE），平均相对误差（δ），相对误差标准差（σ）评价土壤水分的估计效果。

1）平均相对误差δ

δ为10 000组监测点在时间估计土壤水分的平均相对误差，计算公式如下：

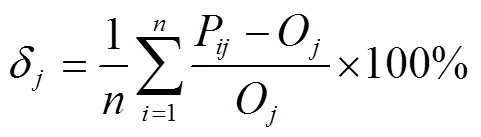
式中(=10 000)是监测点的组数；P为第组监测点在时间的土壤水分的估计值，cm3/cm3；O为时间时实测土壤水分的平均值，cm3/cm3，本文以162个采样点的实测土壤水分平均值作为时间时实测土壤水分的平均值。δ用来判定监测点的土壤水分估计值与实测值的接近程度，其值越小表明估计值与实测值越接近。

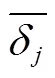
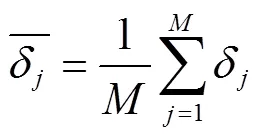
式中为土壤水分的实际测定次数。

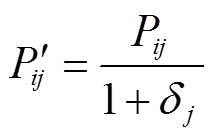
式中′为第组监测点在时间的修正后的土壤水分估计值，cm3/cm3。

2）标准差（σ）

σ为10 000组监测点在时间时对研究区土壤水分进行估计时的相对误差的标准偏差，计算公式如下：

标准差σ反映了监测点的土壤水分估计值与均值的偏离程度，其值越小相对均值的偏离程度越小，预测的精度越高。

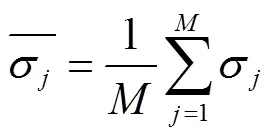
2 结果与分析

2.1 AWC和土壤水分的描述性统计及正态分布检验

表1为0～40和0～80 cm土层AWC描述性统计特征。可以看出0～40和0～80 cm土层均为中等程度变异。其中0～40比0～80 cm土层的变异系数大，主要是因为0～40 cm土层为作物根系的主要分布区和耕作区，试验区农户耕作管理的差异性，加上作物根系分布的不均匀性增加了AWC的空间变异。采用Kolmogorov-Smirnov法对AWC进行正态分布检验，通过正态分布检验，值均大于0.05，检验结果如表1所示，。进行正态分布检验的目的是确保分布可以有效应用于监测点数量的计算，以及可以利用半方差函数分析AWC的空间变异情况[32]。2016—2018年的夏玉米实测土壤水分也服从正态分布。

表1 有效含水量（AWC）描述性统计特征

2.2 AWC空间变异分析

应用地统计学方法对AWC作半方差函数分析，得出2个土层的变程均为366 m，变程代表了AWC的空间自相关范围[33]，变程越大，空间自相关范围越大；反之则越小。在变程范围内监测点存在相关性而非相互独立，而利用公式（2）计算监测点数目时，认为监测点间是相互独立的，因此变程为确定监测点的间距提供了依据[34]。在确定监测点位置时，使任意2个监测点之间的距离大于366 m，可保证监测点相互独立，满足公式（2）的前提。

2.3 土壤水分监测点布设数量

根据AWC的变异系数，采用公式（2）计算0～40和0～80 cm土层的合理监测点布设数量。计算结果表明，在90%置信区间，采样误差为10%时，0～40和0～80 cm土层监测点数分别为7和6个。

2.4 土壤水分监测效果分析

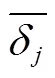
由图2可知，SSAV布点方法δ的变化范围为–0.67%～6.31%，0～40和0～80 cm土层的δ的平均值分别为2.22%和2.12%。SRS布点条件下δ的平均值分别为1.86%和1.55%。这说明2种布点方法均高估监测点土壤水分[31]，在这种情况下可以利用式（8）对土壤水分进行修正[30]。王珊等[41]提出了在AWC的等值线上布设监测点来估计平均土壤水分，其布设的一组监测点估计土壤水分的相对误差范围为1.56%～8.95%，其相对误差的范围与本文SSAV布点法δ（–0.67%～6.31%）的范围相近。SRS和SSAV方法下，0～40和0～80 cm 2个土层9次观测值和估计值之间的平均RMSE分别为0.012 0和 0.010 4 cm3/cm3，显著性检验<0.001，具有显著性差异（表2、表3）。图3为两种布点方法下土壤含水率的估计值与实测值的对比图，由图可知SSAV布点法下两个土层的2值均大于SRS布点法，RMSE值均小于SRS布点法，因此基于SSAV布设的土壤水分监测点对平均土壤水分的估计值与实测值更为接近。

注：SRS为简单随机布点法，SSAV为基于辅助变量空间自相关的分层采样方法。下同。

Note: SRS is simple random sampling method, SSAV is stratified sampling method based on spatial autocorrelation of auxiliary variables. Same as below.

图2 不同采样方法下的土壤水分估计结果

Fig.2 Soil moisture estimation results obtained by different sampling methods

表2 0～40 cm土层相对误差范围、、RMSE的显著性检验

表3 0～80 cm土层相对误差范围、、RMSE的显著性检验

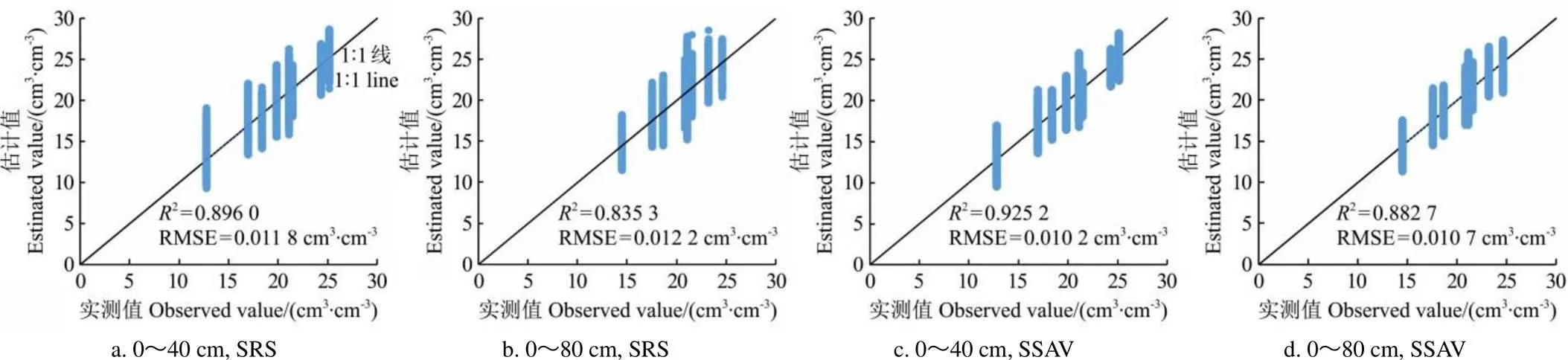
图3 不同采样方法下土壤含水率估计值和实测值对比

3 结 论

土壤水分监测点的合理布设对于农田土壤灌溉管理至关重要，本文构建了考虑有效含水量（Available Water Capacity，AWC）基于辅助变量空间自相关的分层采样方法（Stratified Sampling method based on spatial autocorrelation of Auxiliary Variables，SSAV），并于2016—2018年进行了田间试验，对其估计效果进行了分析，得出以下结论：

1）0～40和0～80 cm土层均为中等变异，监测点的布设数量分别为7个和6个。

SSAV法为获取区域平均土壤含水量数据提供了省时、省力、低成本的监测点布设方案，可为农业水资源管理和提升农业用水效率提供保障。

[1] Gao L, Shao M A. Temporal stability of soil water storage in diverse soil layers[J]. Catena, 2012, 95: 24-32.

[2] Penna D, Brocca L, Borga M, et al. Soil moisture temporal stability at different depths on two alpine hillslopes during wet and dry periods[J]. Journal of Hydrology, 2013, 477: 55-71.

[3] Brocca L, Tullo T, Melone F, et al. Catchment scale soil moisture spatial-temporal variability[J]. Journal of Hydrology, 2012, 422: 63-75.

[4] Jia X X, Shao M A, Wei X X, et al. Hillslope scale temporal stability of soil water storage in diverse soil layers[J]. Journal of Hydrology, 2013, 498: 254-264.

[5] Famiglietti J S, Ryu D, Berg A A, et al. Field observations of soil moisture variability across scales[J]. Water Resource Research, 2008, 44: W01423.

[6] 王春梅，占玉林，魏香琴，等. 非均质中低分辨率像元土壤含水量地面采样方法研究进展[J]. 中南大学学报：自然科学版，2016，47(4)：1414-1419.

Wang Chunmei, Zhan Yulin, Wei Xiangqin, et al. Ground sampling strategy for surface soil moisture in heterogeneous remote sensing pixels[J]. Journal of Central South University: Science and Technology, 2016,47(4): 1414-1419. (in Chinese with English abstract)

[7] 陈天恩，陈立平，王彦集，等. 基于地统计的土壤养分采样布局优化[J]. 农业工程学报，2009，25（增刊2）：49-55.

Chen Tian’en, Chen Liping, Wang Yanji, et al. Optimal arrangement of soil nutrient sampling based on geo-statistics[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25 (Supp.2): 49-55. (in Chinese with English abstract)

[8] Brocca L, Melone F, Moramarco T, et al. Spatial-temporal variability of soil moisture and its estimation across scales[J]. Water Resource Research, 2010, 46(2): W02516.

[9] Wang C M, Zuo Q, Zhang R D, Estimating the necessary sampling size of surface soil moisture at different scales using a random combination method[J]. Journal of Hydrology, 2008, 352: 309-321.

[10] Korres W, Reichenau T G, Schneider K. Patterns and scaling properties of surface soil moisture in an agricultural landscape: An ecohydrological modeling study[J]. Journal of Hydrology, 2013, 498: 89-102.

[11] Pachepsky Y, Radcliffe D, Selim H M. Scaling methods in soil physics[M]. New York: CRC Press LLC, 2002: 102−103.

[12] Wang J, Fu B J, Chen L D, et al. Geostatistical analysis of soil moisture variability on Da Nangou catchment of the loess plateau, China[J]. Environmental Geology 2001, 41: 113-120.

[13] 李子忠，龚元石. 农田土壤水分和电导率空间变异性及确定其采样数的方法[J]. 中国农业大学学报，2000，5(5)：59-66.

Li Zizhong, Gong Yuanshi. Spatial variability of soil water content and bulk soil electrical conductivity and determination of sampling number in field[J]. Journal of China Agricultural University, 2000, 5(5): 59-66. (in Chinese with English abstract)

[14] 薛正平，杨星卫，段项锁，等. 土壤养分空间变异及合理取样数研究[J]. 农业工程学报，2002，18(4)：6-9.

Xue Zhengping, Yang Xingwei, Duan Xiangsuo, et al. Spatial variability of soil nutrient and reasonable sampling number[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2002, 18(4): 6-9. (in Chinese with English abstract)

[15] 尤冬梅. 农田土壤重金属污染监测及其空间估值方法研究[D]. 北京：中国农业大学，2014.

You Dongmei. Monitoring and Spatial Estimation of Contents of Soil Heavy Metals[D]. Beijing: China Agricultural University, 2014. (in Chinese with English abstract)

[16] 赵倩倩，赵庚星，姜怀龙，等. 县域土壤养分空间变异特征及合理采样数研究[J]. 自然资源学报，2012，27(8)：1382-1391.

Zhao Qianqian, Zhao Gengxing, Jiang Huailong, et al. Study on spatial variability of soil nutrients and reasonable sampling number at county scale[J]. Journal of Natural Resources, 2012, 27(8): 1382-1391. (in Chinese with English abstract)

[17] 陈伟杰. 土壤特性的优化采样策略及空间离群样点监测算法研究[D]. 哈尔滨：东北农业大学，2019.

Chen Weijie. Research on the Sampling Strategies for Soil Properties and A Method for Spatial Local Outlier Detection[D]. Harbin: Northeast Agricultural University, 2019. (in Chinese with English abstract)

[18] 陈飞香，戴慧，胡月明，等. 区域土壤空间抽样方法研究[J]. 地理与地理信息科学，2012，28(6)：53-56.

Chen Feixiang, Dai Hui, Hu Yueming, et al. Study on regional soil spatial sampling method[J]. Geography and Geo-Information Science, 2012, 28(6): 53-56. (in Chinese with English abstract)

[19] 朱爽，张锦水. 面向省级农作物种植面积遥感估算的分层方法[J]. 农业工程学报，2013, 29(2)：184-191.

Zhu Shuang, Zhang Jinshui. Provincial agricultural stratification method for crop area estimation by remote sensing[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(2): 184-191. (in Chinese with English abstract)

[20] 曹志冬，王劲峰, 李连发，等. 地理空间中不同分层抽样方式的分层效率与优化策略[J]. 地理科学进展，2008，27(3)：152-160.

Cao Zhidong, Wang Jinfeng, Li Lianfa, et al. Strata efficiency and optimization strategy of stratified sampling on spatial population[J]. Progress in Geography, 2008, 27(3): 152-160. (in Chinese with English abstract)

[21] Cochran W G. Sampling Techniques (3rd editioned)[M]. New York: John Wiley & Sons, 1977.

[22] Dunn R, Harrison A R. Two-dimensional systematic sampling of land use[J]. Applied Statistics, 1993, 42(4): 585-601.

[23] 高晓东. 黄土丘陵区小流域土壤有效水时空变异与动态模拟研究[D]. 北京：中国科学院大学，2013.

Gao Xiaodong. Catchment-Scale Available Soil Moisture Spatial-Temporal Variability in the Hilly Areas of the Loess Plateau[D]. Beijing: University of Chinese Academy of Sciences, 2013. (in Chinese with English abstract)

[24] 高晓东，吴普特，张宝庆，等. 黄土丘陵区小流域土壤有效水空间变异及其季节性特征[J]. 土壤学报，2015，52(1)：57-67.

Gao Xiaodong, Wu Pute, Zhang Baoqing, et al. Spatial variability of available soil moisture and its seasonality in a small watershed in the hilly region of the Loess Plateau[J]. Acta Pedologica Sinica, 2015, 52(1): 57-67. (in Chinese with English abstract)

[25] Zhao W X, Li J S, Yang R M, et al. Determining placement criteria of moisture sensors through temporal stability analysis of soil water contents for a variable rate irrigation system[J]. Precision Agric, 2018, 19: 648-665.

[26] Jacobs J M, Mohanty B P, Hsu E, et al. SMEX02: Field scale variability, time stability and similarity of soil moisture[J]. Remote Sensing of Environment, 2004, 92: 436-446.

[27] Miyamoto S, Chacon A, Hossain M, et al. Soil salinity of urban turf areas irrigated with saline water: I. spatial variability[J]. Landsc Urban Plan, 2005, 71: 233-241.

[28] Hupet F, Vanclooster M. Sampling strategies to estimate field real evapotranspiration fluxes with a soil water balance approach[J]. Journal of Hydrology, 2004, 292: 262-280.

[29] Manly B F J. Randomization, Bootstrap and Monte Carlo Methods in Biology (2nd editioned)[M]. London: Chapman & Hall Press, 1997, 56-60.

[30] Zhang P P, Shao M A. Temporal stability of surface soil moisture in a desert area of northwestern China[J]. Journal of Hydrology, 2013,505: 91-101.

[31] 朱绪超，邵明安，朱军涛，等.高寒草甸生态系统表层土壤水分时间稳定性研究[J]. 农业机械学报，2017，48(8)：212-218.

Zhu Xuchao, Shao Ming’an, Zhu Juntao, et al. Temporal stability of surface soil moisture in alpine meadow ecosystem on northern tibetan plateau[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(8): 212-218. (in Chinese with English abstract)

[32] Shi Z, Wang K. Sampling strategies for mapping soil phosphorus and soil potassium distributions in cool temperate grassland[J]. Precision Agriculture, 2000, 2: 347-357.

[33] Petrone R M, Price J S, Carey S K. Statistical characterization of the spatial variability of soil moisture in a cutover peatland[J]. HydrologicalProcessed 2004, 18: 41-52.

[34] Webster R. Quantitative spatial analysis of soil in the field[J]. Advance in Soil Science, 1985, 3: 1-70.

[35] 李民赞．基于可见光光谱分析的土壤参数分析[J]．农业工程学报，2003，19(5)：109-113．

Li Minzan. Evaluating soil parameters with visible spectroscopy[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2003, 19(5): 109-113. (in Chinese with English abstract)

[36] 连健，李小娟，宫辉力，等. GIS支持下的空间分层抽样方法研究——以北京市人均农业总产值抽样调查为例[J]. 地理与地理信息科学，2008，24(6)：30-38.

Lian Jian, Li Xiaojuan, Gong Huili, et al. Research of spatial stratified sampling techniques based on GIS: Take the per capita agricultural total output value sampling survey of Beijing as an example[J]. Geography and Geo- Information Science, 2008, 24(6): 30-38. (in Chinese with English abstract)

[37] De Gruijter J J, Brus D J, Bierkens M F P, et al. Sampling for natural resource monitoring[M]. Springer: Netherlands, 2006.

[38] Haining R P. Spatial Data Analysis: Theory and Practice[M]. Cambridge: Cambridge University, 2003.

[39] 仲格吉. 空间相关性和变异性对农作物面积空间抽样效率的影响研究[D]. 北京：中国农业科学院，2019.

Zhong Geji. Impacts of Spatial Correlation and Variability on the Spatial Sampling Efficiency for Crop Acreage Estimation[D]. Beijing: Chinese Academy of Agricultural Sciences, 2019. (in Chinese with English abstract)

[40] Falk M G, Denham R J. Mengersen K L. Spatially stratified sampling using auxiliary information for geostatistical mapping[J]. Environmental And Ecological. Statistics. 2011, 18: 93-108.

[41] 王珊，胡振华，张宝忠，等. 基于有效最大含水量的土壤水分监测优化布设方法[J]. 中国农村水利水电, 2018(5): 1-5.

Wang Shan, Hu Zhenhua, Zhang Baozhong, et al. Optimum layout method of soil moisture monitoring on the basis of available maximum water content[J]. 2018(5): 1-5. (in Chinese with English abstract)

Spatial stratified sampling strategy for soil moisture based on available water capacity

Jin Jianhua1,2,3, Zhang Baozhong1,4※, Liu Yu1,4, Mao Xiaomin2

(1.100038;2.100083; 3.300384;4.100048)

Soil moisture has been a key limiting factor for crop growth during the surface process in many lands. It is very necessary to establish the placement criteria of monitoring sites for the soil moisture in optimum irrigation. The spatial and temporal distribution of Available Water Capacity (AWC) was strongly correlated with soil moisture. The AWC spatial distribution pattern was also related to soil characteristics, but it can be more stable than that of soil moisture. In this study, a spatially stratified sampling was proposed to relieve the strong temporal and spatial variability, when the soil moisture was used as a variable. The Stratified Sampling method based on spatial autocorrelation of Auxiliary Variables (SSAV) was also used to combine the classical statistics and geo-statistics, where the AWC was introduced as an auxiliary variable. The experiments were then carried out to verify at a field scale. The results showed that the AWC in the 0-40 and 0-80 cm soil layers followed the normal distribution, indicating a moderate variation. In the 90% confidence interval, the number of monitoring points in the 0-40 and 0-80 cm soil layers in the study area was 7 and 6, respectively, where the sampling error was 10%, indicating that the reducing number of monitoring points, and cost-saving monitoring of soil moisture. The geostatistical analysis demonstrated that the range of two soil layers (0-40 and 0-80 cm) was both 366 m in the semi-variance function of AWC. The relative errors of soil moisture estimated by the Simple Random Sampling (SRS) and SSAV were –27.03%-52.38%, and –23.23%-35.15%, respectively. The relative error of soil moisture estimated by the SSAV was reduced by 26.48%, compared with the SRS. The mean standard deviation was 4.78%, 17.30% lower than that of SRS. A paired-test indicated that the relative error and the mean standard deviation of soil moisture were 9 times in the two soil layers under two monitoring during 2016-2018. Thus, there were significant differences between the relative error range and the mean standard deviation under two monitoring (<0.001). Moreover, the uncertainty of SSAV was reduced significantly, whereas, the estimation accuracy was improved significantly, compared with the SRS. Among them, the uncertainty of SRS was attributed to the independent samples that followed the normal distribution. There was also a certain spatial change of soil characteristics at a certain scale, indicating a spatial correlation. Correspondingly, the larger deviation of estimation accuracy was attributed to the SRS model without considering the spatial autocorrelation of soil moisture. The Root Mean Square Error (RMSE) between the observed and estimated values was only 0.010 4 cm3/cm3, indicating significantly lower than that of the SRS (0.012 0 cm3/cm3). As such, the uncertainty of sampling was reduced according to the value range of AWC. The new sampling was fully considered the influence of the spatial structure of the target variable on the layout of monitoring points. Specifically, the distance between any two monitoring points was required to be greater than the range, where the monitoring points were independent of each other. Therefore, the estimation accuracy and precision of soil moisture were improved, compared with the SRS. Consequently, the SSAV can be widely expected to serve a time-, labor- and cost-saving monitoring scheme for the average soil moisture. The finding can provide a promising guideline for water resources management and water use efficiency in modern agriculture.

soils; moisture; sampling; geo-statistics; available water capacity; spatial autocorrelation; spatial variability

10.11975/j.issn.1002-6819.2021.21.012

S127

A

1002-6819(2021)-21-0100-08

金建华，张宝忠，刘钰，等. 基于有效含水量的土壤水分监测点布设的空间分层采样方法[J]. 农业工程学报，2021，37(21)：100-107.doi：10.11975/j.issn.1002-6819.2021.21.012 http://www.tcsae.org

Jin Jianhua, Zhang Baozhong, Liu Yu, et al. Spatial stratified sampling strategy for soil moisture based on available water capacity[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(21): 100-107. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2021.21.012 http://www.tcsae.org

2021-08-02

2021-10-23

国家自然科学基金项目（51822907，51979287）；流域水循环模拟与调控国家重点实验室自主研究项目（SKL2020TS08）；天津市教委科研计划项目（2018KJ189）

金建华，讲师，研究方向为节水灌溉与水资源高效利用。Email：jinjh2010@163.com

张宝忠，博士，教授级高级工程师，研究方向为蒸散发尺度效应、现代灌区高效用水理论与技术研究。Email：zhangbz@iwhr.com