流冰对输水明渠混凝土衬砌的撞击影响

贡 力，贾治元，李义强，杜强业，张娇艳

流冰对输水明渠混凝土衬砌的撞击影响

贡 力，贾治元，李义强，杜强业，张娇艳

（兰州交通大学土木工程学院，兰州 730070）

为研究西北寒冷地区长距离输水工程中流冰对输水明渠的撞击影响，该研究运用LS-DYNA软件模拟不同工况下流冰与输水明渠碰撞挤压过程，并通过室内模型试验进行相应验证，探求水-空气耦合介质中流冰碰撞输水明渠的破坏规律。结果表明：流冰速度对明渠衬砌撞击的最大等效应力与方向最大位移呈现出近似的Pseudo-Voigt函数峰值曲线关系。流冰压缩强度对明渠衬砌撞击的最大等效应力与方向最大位移呈现出近似的线性关系。综合分析所模拟的不同组合工况可以看出，对明渠衬砌撞击影响明显的组合区间是流冰压缩强度为1.825～3.199 MPa、流冰速度为3.5～4.5 m/s时的组合情况，其等效应力值为4.3～16.8 MPa、方向最大位移值为2.59×10-5～5.52×10-5m；对明渠衬砌撞击影响最大的双因素组合是流冰压缩强度为3.059 MPa、流冰速度为4.0 m/s的组合情况，其等效应力值为16.8 MPa、方向最大位移值为5.52×10-5m；对明渠衬砌撞击影响较为不明显的组合区间是流冰速度为0.5～1.0 m/s、压缩强度为1.825～ 2.375 MPa时的组合情况，其等效应力为0.7～2.8 MPa、方向最大位移为0.24×10-5～0.52×10-5m。同时，模拟值与试验结果基本吻合，表明所采用的数值模拟仿真模型准确可靠，其结果可为寒冷地区冬季输水工程安全运营提供帮助。

数值模拟；试验；流固耦合；流冰；明渠；撞击影响

0 引 言

西北地区冬季寒冷，流冰期长，冰凌灾害已经成为该地区农业灌溉输水工程中的首要问题[1]。位于此地区的输水明渠在农田灌溉输水过程中，经常受到水-空气-流冰耦合作用下的撞击，而长期的流冰碰撞会导致输水明渠混凝土衬砌龟裂或表层剥落等破坏，对输水明渠衬砌结构安全以及长期农田灌溉供水稳定性方面存在着严重的威胁。

国内外学者在流冰碰撞仿真模拟方面进行了大量的研究。Tuhkuri[2]利用弹性断裂理论与边界单元法建立了各向同性冰排与结构相互作用的数值模型，进行了冰排裂纹形成过程的研究；蔡伟等[3]开展了与实验场景相对应的不同冰材料模型下的船冰碰撞有限元数值模拟，总结了用于船-冰碰撞数值模拟的冰材料模型准确性和可行性评估方法；Sand等[4]考虑了水压力、浮力、冰材料的断裂与破碎等因素后，将各项同性冰材料模型与结构体相互作用进行了系统的有限元仿真模拟研究；贡力等[5]在流冰对输水隧洞撞击作用力学特性方面进行了相应的研究与分析；Rüdiger等[6]考虑模型尺度的冰微观结构和荷载作用下各种物理效应的数值模型；张宿峰[7]基于线弹性材料模型冰排特性和桥墩破冰形状对流冰撞击力的影响；Zhang等[8]利用LS-DYNA软件对影响流冰和T型刚构桥桥墩接触碰撞过程的因素进行了研究分析；黄焱等[9]对船-冰碰撞载荷时间历程的模型试验进行了研究；Miryaha[10]研究了典型的浮冰作用模式和海上结构的应力分布。王健伟等[11]基于非线性有限元法对船-冰层碰撞结构响应研究。综上所述，国内外学者在流冰碰撞桥墩和船冰碰撞方面的研究较多，但针对流冰对寒冷地区输水明渠的撞击作用研究较少。

为研究寒冷地区长距离输调水工程中水-空气-流冰耦合作用下对输水明渠混凝土衬砌的撞击影响，探究水-空气耦合介质中流冰碰撞输水明渠混凝土衬砌破坏规律，本文采用数值模拟结合模型试验的方法，并运用 ANSYS/LS-DYNA 建立水-空气耦合介质中流冰与输水明渠之间发生碰撞的有限元模型，模拟流冰与输水明渠混凝土衬砌碰撞过程，发现流冰在不同工况下对输水明渠的撞击影响规律，拟为寒冷地区冬季输调水工程安全运营提供技术支撑。

1 流冰-明渠碰撞仿真模型

1.1 仿真分析理论

1.1.1 显示时间积分原理

根据牛顿定律得流冰碰撞明渠运动方程如(1)所示：

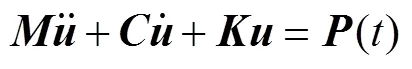
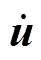
在考虑阻尼沙漏后，式（1）变为矩阵形式[12]，如式（2）：

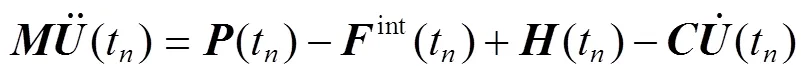
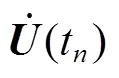
由式（2）可以得到t时刻的加速度如式（3）。

(t)=-1[(t)–int(t)+(t)–(t)] （3）

式中(t)为位移列阵。

根据公式（4)、（5)可以求出t+1时刻的速度和位移。

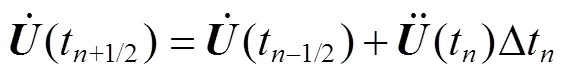
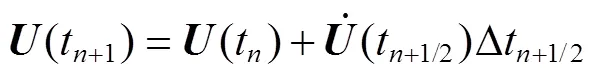
1.1.2 接触碰撞算法与类型

运用LS-DYNA软件模拟流冰与明渠碰撞问题时，碰撞过程中的接触问题计算分析以罚函数法为主[13]，罚函数法为在时间步∆中检查到穿透主面的从节点，则将会在被穿透面中间引入一个界面接触力[14]。该接触力称为罚函数值，如公式（6）所示。

=（6）

式中为罚函数值，N；为接触界面刚度,N/mm；为穿透量,mm。

接触面力应遵守作用力与反作用力原理，并满足条件（7）、（8）。

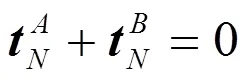
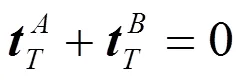
1.1.3 流固耦合

基于本文所述的流冰-明渠碰撞场景，考虑到明渠中存在的水介质与空气介质而建立的水-空-流冰耦合关系，因此在LS-DYNA软件分析显式动力学问题时选用关键字*CONSTRAINED-LAGRANGE-IN-SOLID来定义流固耦合，添加任意拉格朗日欧拉（Arbitrary Lagrange-Euler）算法来区分水介质和空气介质，实现拉格朗日（Lagrangian）算法与欧拉（Euler）算法的相互作用。

1.2 工程实例

本文选取“引大入秦”工程总干渠00+406.92～04+ 231.08段梯形明渠为原型建模。引大入秦总干渠为天祝县境内的天堂寺渠首至永登县庄浪河西岸香炉山总水闸段，全长87 km，年输水量为4.43亿m3，控制灌溉面积可达5.73万hm2，设计引水量为32 m³/s，加大引水量为36 m³/s，设计水深2.29 m，加大水深3.37 m。该明渠底板为C25钢筋混凝土浇筑，厚0.2 m，边坡挂钢筋网浇筑C25细粒混凝土，厚0.12 m，底宽4.6 m，渠高4.1 m，边坡1：1.25。因为考虑到碰撞作用以及计算时间的问题，故而选取对称明渠的一半来进行模型的建立与求解分析，水-空气耦合介质中流冰与明渠衬砌碰撞模型图如图1所示。

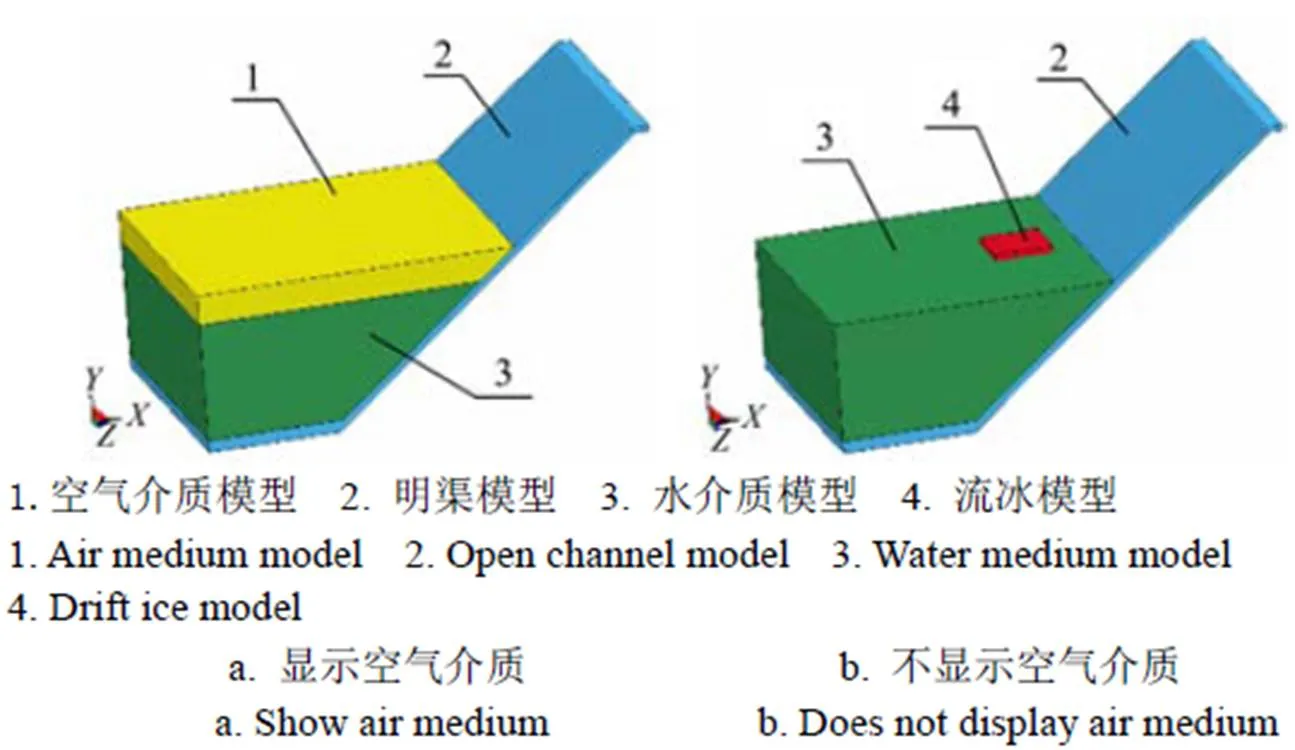
图1 水-空气耦合介质中流冰与明渠衬砌碰撞模型图

为减少计算时间，接近真实碰撞情形，选取(7.582 9 m + 2.307 9 m)×4.1 m×0.5×5 m的梯形明渠模型、(5.432 9 m + 4.8079 m)×0.5 m×0.5×5 m的梯形空气介质模型和(4.807 9 m+2.307 9 m)×2 m×0.5×5 m的梯形水介质模型，其中梯形模型截面面积按照（上底+下底）×高×0.5计算，模型总长度均为5 m。本文以大通河冰情和明渠所在地理位置为依据，并参考徐国宾等[15]在流冰方面的研究，选取为1 m×1 m×0.5 m的长方体流冰模型，其中流冰厚度为0.5 m，碰撞面积为0.5 m2。

1.3 模型材料参数的选取

1）流冰模型材料参数

流冰模型材料参数参考杨亮等[16]的研究成果，冰材料模型参数如表1所示。

表1 冰材料模型参数

2）输水明渠衬砌混凝土材料

明渠衬砌混凝土材料模型由Federal Highway Administration开发，并运用于模拟混凝土结构低速冲击碰撞方面[17]，混凝土材料模型参数如表2所示。

3）水-空气耦合介质材料参数

在软件LS-DYNA 中，水介质和空气介质采用空白材料组进行定义，关键字为*MAT_NULL，由文献[18]可知，水介质材料密度参数为1000 kg/m3、截断应力为–1×105Pa，空气介质材料密度参数为1.184 5 kg/m3、截断应力为 –10 Pa。定义状态方程时，水介质采用Gruneisen状态方程，空气介质采用Polynomial状态方程，水-空气状态方程参数[19]如表3所示。

表2 混凝土材料模型参数

表3 水-空气状态方程参数

注：0为初始相对体积；0为初始内能。

Note:0is the initial relative volume;0is the initial internal energy.

1.4 有限元模型

ANSYS/LS-DYNA适用于模拟各类真实环境中的复杂问题，能够求解三维非弹性结构在高速碰撞、爆炸冲击下的大变形动力响应。作为一款通用的非线性有限元分析软件，可以进行包括几何非线性（如位移、应变和转动）、材料的非线性（如多种材料动态模型）及接触非线性等分析。在算法上以Lagrange算法为主，此外还有ALE和 Euler算法；在求解上以显示求解为主，同时兼有隐式求解功能；主要功能为结构分析，同时兼备热分析、流固耦合功能；分析上以非线性动力为主，以静力分析为辅。

流冰与明渠衬砌的碰撞因素主要包括：流冰压缩强度、流冰初速度、流冰体积、碰撞面积、流冰厚度、空气介质以及水介质作用等[20]。由于冰水两相之间运动是非常复杂的，其间存在着粘滞力、拖曳力等多因素耦合影响的问题，若改变流冰尺寸，则水介质对不同尺寸的流冰其粘滞力、拖曳力是不一致的，比如流冰质量增加后，水介质的粘滞力和拖曳力增加，使得水流的挟冰能力下降，撞击力则变缓。因此，在模拟时将体积、面积、厚度等参数作为一个定值不变，而将流冰流速、压缩强度作为变量，意在减小流冰“尺寸效应”对模拟结果的影响。从而只探究流冰在不同流速、不同压缩强度工况下对输水明渠衬砌的等效应力及明渠碰撞区位移进行分析。

将材料参数设置好后，建立水-空气耦合介质中流冰与明渠混凝土衬砌的有限元碰撞模型，采用SWEEP网格划分，水-空气耦合介质中流冰与明渠衬砌碰撞网格划分图如图2所示。水、空气、流冰和输水明渠模型均采用3D Solid164实体单元，求解过程中将流冰与输水明渠设置为面面自动接触类型，明渠衬砌面为主面，流冰接触面为从面。由于漂浮在水面的流冰处于竖向平衡状态,所以在仿真模拟时忽略了流冰所受的竖向荷载，仅考虑水流拖动流冰运动的水平荷载,而其水平荷载主要通过给流冰设置初速度（初速度方向即明渠衬砌方向）来体现，水流不提供使流冰水平运动的动力。因此，在模拟计算中并没有对水流设置速度，水介质处于静止状态。流速不同、压缩强度不一的流冰作用于明渠衬砌时，不同工况下的撞击影响也是不同的。给流冰假设初速度及边界条件后进行输出控制，输出K文件进行计算。为了减小计算时间，在模拟时将流冰与衬砌距离设置为 0.005 m，求解时间设置为0.1 s进行求解，不考虑二次碰撞等问题。在这样一个短距离和一个短时间内的单次碰撞问题中，流冰对明渠衬砌撞击区的方向起主要作用，对方向的影响很小，因此在分析计算时仅对明渠撞击区方向做相应的说明。

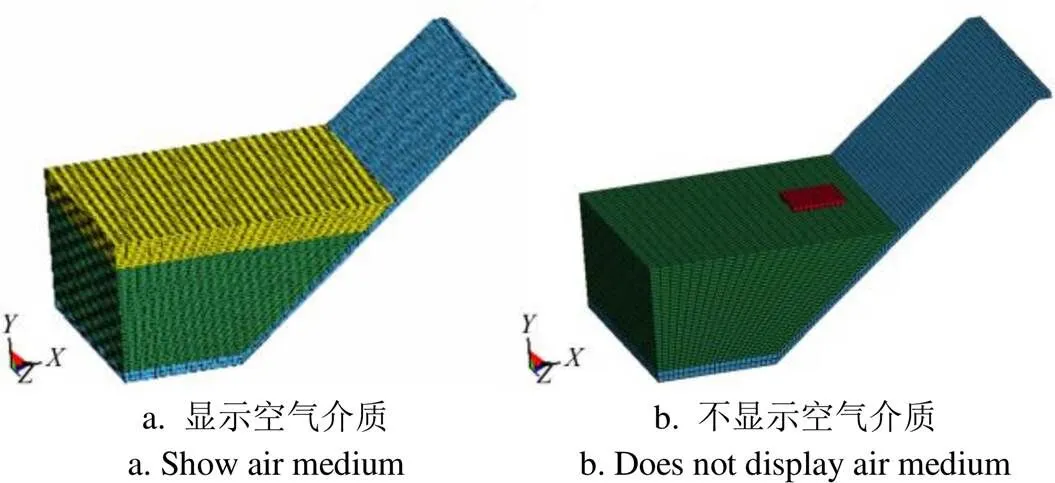
图2 水-空气耦合介质中流冰与明渠衬砌碰撞网格划分图

1.5 工况的选取

1）不同流冰流速工况的选取

根据引大入秦工程设计流速与最大流速并参考文献[21]建立了0.5、1.0、1.5、2.0、2.5、3.0、3.5、4.0、4.5、 5.0 m/s这10种流速工况下流冰与明渠衬砌的碰撞方案。根据引大入秦工程运营设计水深及最大水深，选取模拟水深为2.0 m。

2）不同流冰压缩强度工况的选取

流冰压缩强度随着温度产生变化，温度越低，流冰压缩强度越大。根据天堂水文站实测资料推得冬季平均气温在–5℃左右，极端最低气温为–28.3℃，并参照王庆凯等[22]对黄河冰单轴压缩强度的试验，可知流冰压缩强度与温度数据如表4所示。

表4 流冰压缩强度与温度数据表

2 仿真结果与分析

2.1 组合工况下的仿真结果

流冰速度工况范围为0.5～5 m/s，考虑到3.5 m/s为中间值，具有代表性，因此选择速度为3.5 m/s进行典型分析。流冰压缩强度对应温度，如表4，考虑到该地区冬季平均气温在–5°左右，对应流冰压缩强度为1.825 MPa，因此选取温度–5°对应的压缩强度为1.825 MPa进行求解分析。经模拟计算可知，流冰速度为3.5 m/s、流冰压缩强度为 1.825 MPa双因素组合工况下，明渠衬砌的方向位移和最大等效应力云图与时程曲线分别如图3、图4所示。

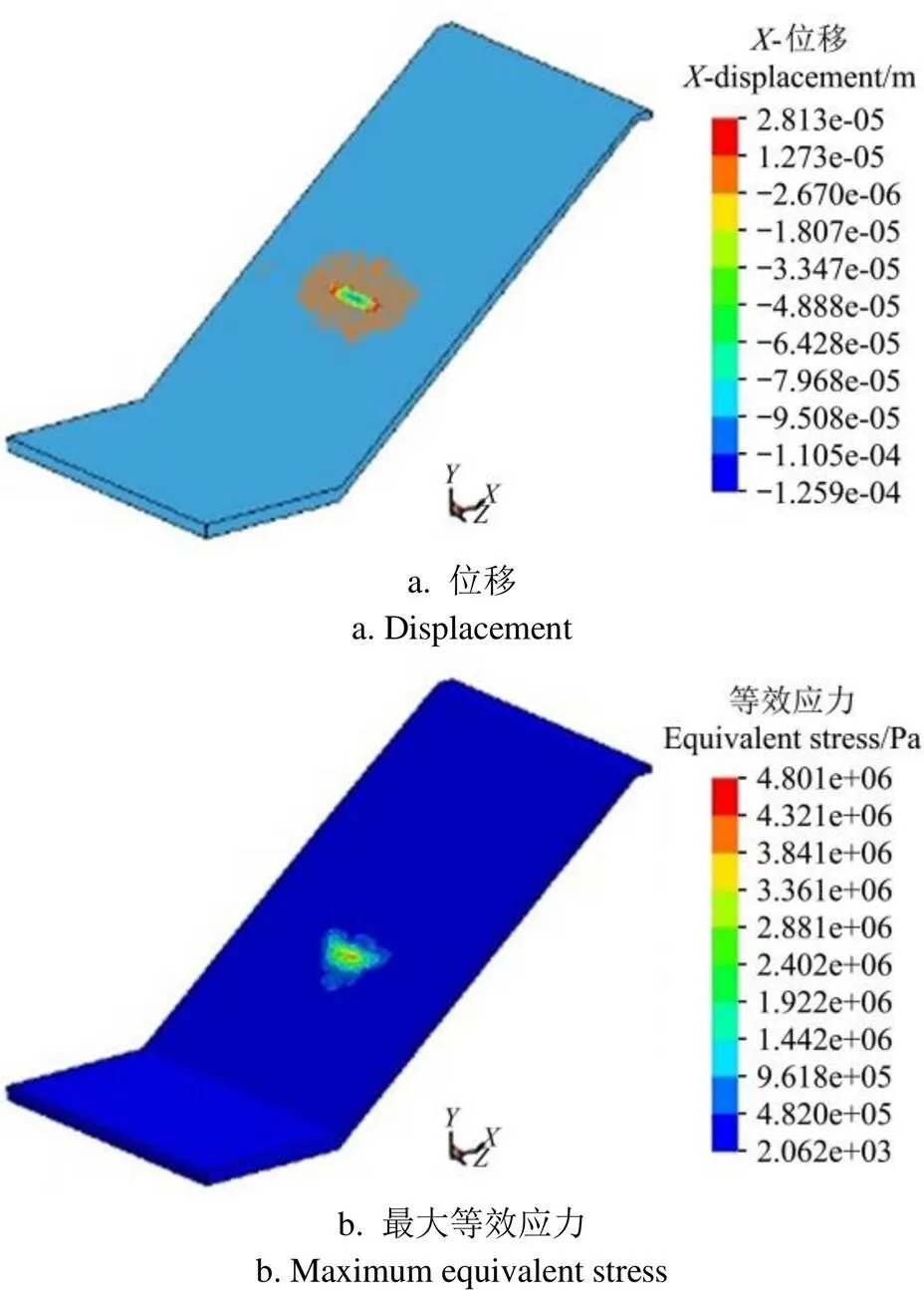
图3 明渠衬砌的X方向位移和最大等效应力云图

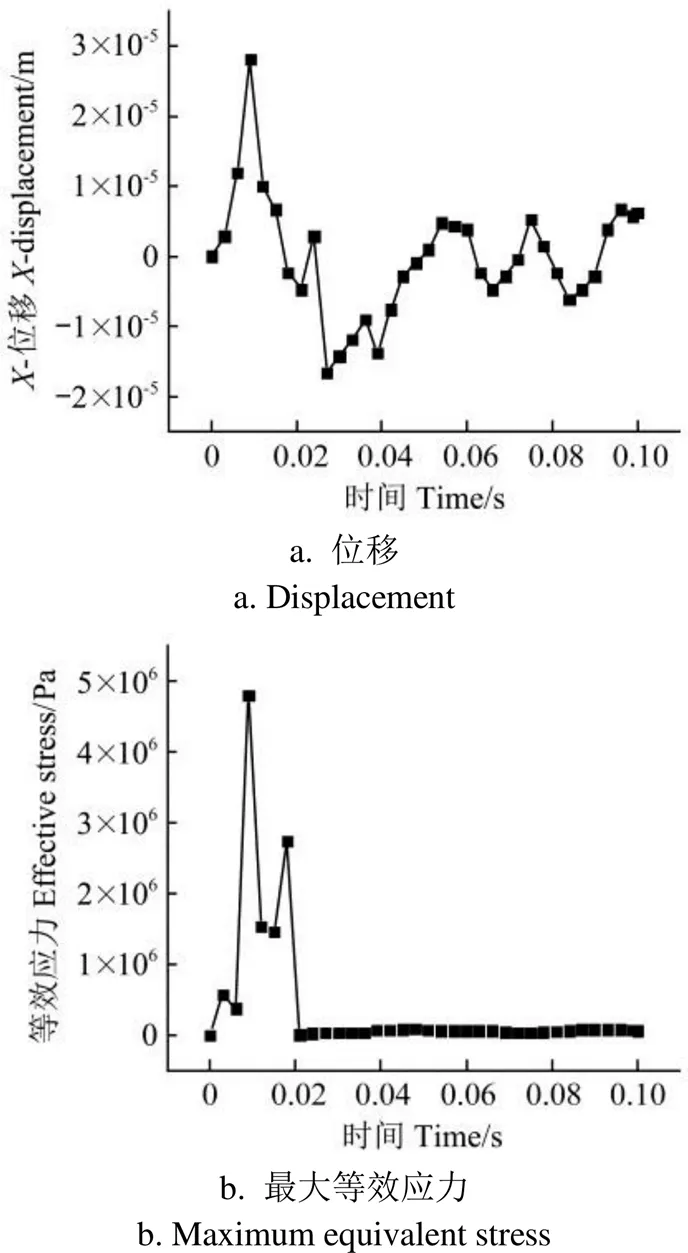
图4 明渠衬砌的X方向位移和最大等效应力时程曲线图

由图3、图4可知，当=0.008 995 2 s，流冰速度为3.5 m/s、流冰压缩强度为1.825 MPa组合工况下的明渠混凝土衬砌撞击区的方向最大位移与最大等效应力分别为2.81×10-5m、4.8×106Pa。

由于水-空气耦合介质中流冰与明渠衬砌的碰撞属于动态响应的过程，因此图4a中明渠衬砌的方向位移时程曲线在不同时刻出现多峰值情况。当=0.008 995 2 s时的峰值为流冰撞击到明渠衬砌的作用峰值，是整个碰撞过程中的最大峰值，明渠衬砌撞击区的位移值在此时也为最大，为2.81×10-5m。在=0～0.008 995 2 s时，撞击区的位移呈现出近似线性增长的趋势，是由于流冰撞向明渠衬砌是一个逐渐逼近的过程，流冰与明渠衬砌之间的水-空气耦合介质会形成一个高应力场先对明渠衬砌产生作用。在=0.008 995 2 s以后撞击区位移由最大峰值下降到有稳定的趋势且出现多个振幅，是由于流冰撞击到明渠衬砌的后构件发生了的不断失效破坏，此时明渠衬砌出现弹性变形。

由图4b知，在=0～0.008 995 2 s时，即荷载加载阶段出现中间峰值，且整体呈现出近似线性增长，是因为流冰在撞向明渠衬砌的过程中，流冰与明渠衬砌之间的水-空气耦合介质对明渠衬砌产生的挤压作用。当= 0.008 995 2 s时，出现最大峰值，为流冰撞击到明渠衬砌的作用峰值，明渠衬砌受撞击区的撞击应力在此时也达到最大值4.8×106Pa。在=0.008 995 2 s以后撞击区等效应力由最大峰值下降到趋于0阶段内，即荷载卸载阶段出现中间峰值，可以看成是由于撞击过程中产生的波浪或者碎冰对明渠衬砌的影响。

2.2 不同组合工况下的仿真结果分析

2.2.1 不同压缩强度下流冰速度对明渠衬砌的影响

由2.1节对图3、图4数据分析结果同理可知，流冰压缩强度为1.825 MPa时，流冰速度为0.5、1.0、1.5、2.0、2.5、3.0、3.5、4.0、4.5、5.0 m/s工况下对应的明渠碰撞区的最大等效应力分别为0.7×106、0.8×106、1.1×106、1.7×106、2.3×106、3.2×106、4.8×106、8.1×106、4.3×106、3.6×106Pa，所对应的方向最大位移分别为0.24×10-5、0.52×10-5、0.57×10-5、0.61×10-5、0.73×10-5、0.89×10-5、2.81×10-5、2.91×10-5、2.59×10-5、2.27×10-5m。分析不同流冰速度与最大等效应力、方向最大位移的关系，绘制如图5、6所示拟合曲线图。

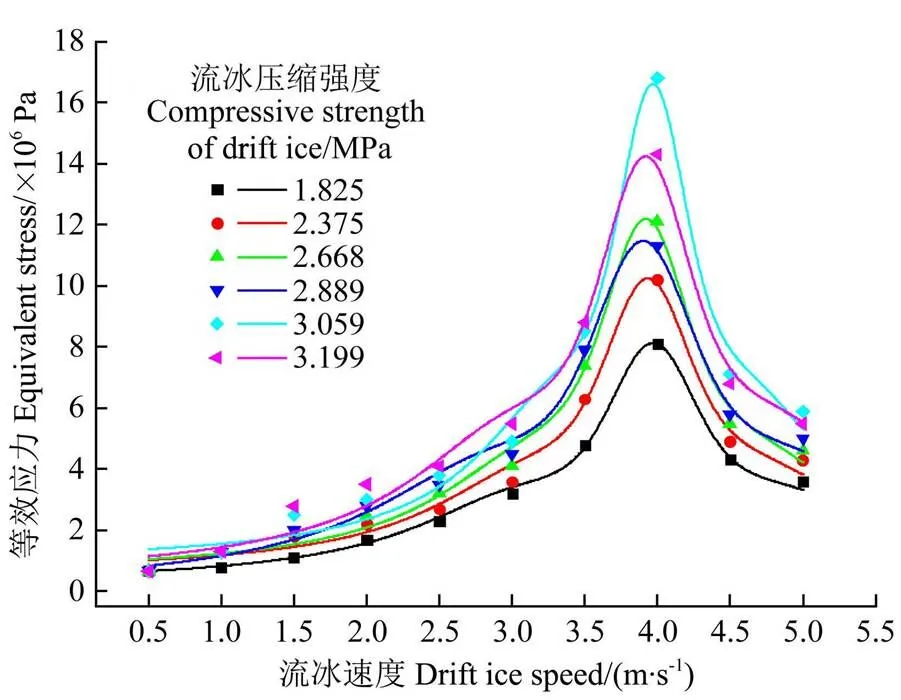
注：不同形状符号为试验值，相应实线为拟合曲线。下同。

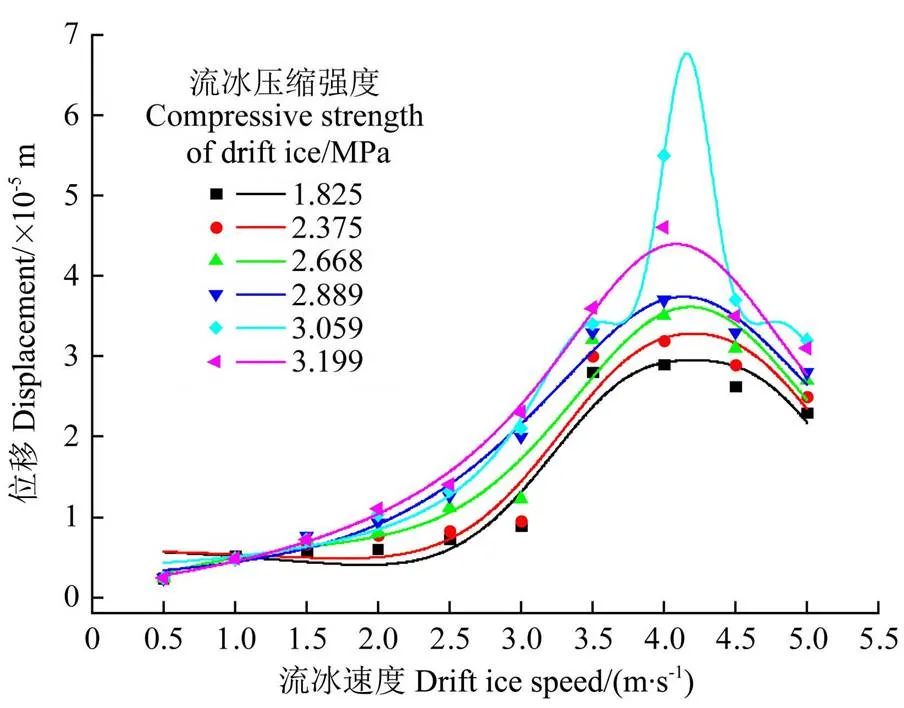
图6 流冰速度与X方向最大位移的关系

由图5可以看出,当流冰压缩强度不变，流冰速度在0.5～4.0 m/s范围时，明渠混凝土衬砌撞击区所受最大等效应力随着流冰速度的增大而增大；流冰速度在4.0 m/s时，明渠混凝土衬砌撞击区所受最大等效应力均出现最大“峰值”；流冰速度在4.0～5.0 m/s范围时，明渠混凝土衬砌撞击区所受最大等效应力随着流冰速度的增大而减小，说明流冰速度在0.5～4 m/s时，其刚性效果起主要作用，流冰速度在4～5 m/s时，其塑性效果其起主要作用。经曲线拟合后明渠混凝土衬砌撞击区所受最大等效应力随流冰速度的增大整体呈现出“单峰”现象，其变化在不同流冰压缩强度工况下均呈现出Pseudo-Voigt函数“峰值曲线”关系，不同压缩强度下流冰速度与最大等效应力的Pseudo-Voigt函数“峰值拟合曲线”关系如公式（9）所示，不同压缩强度下对应的公式（9）中的各项数值见表5。

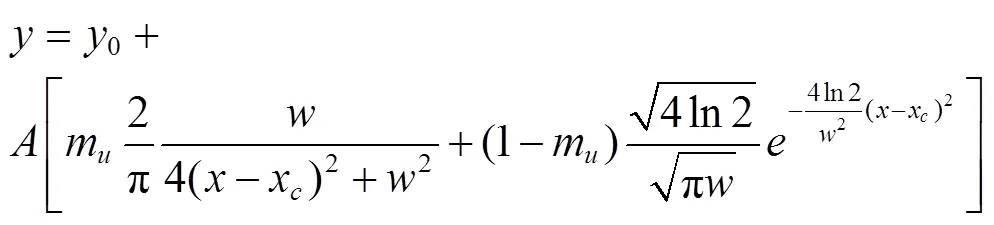
式中为最大等效应力，Pa；为流冰速度，m/s；0为偏移量，Pa；为面积，m2；为半高宽，m/s；x为正中心；m为剖面形状因子。

表5 不同压缩强度下对应拟合曲线中的各项数值

由图6可以看出，当流冰压缩强度不变，流冰速度在0.5～4.0 m/s范围时，明渠撞击区方向最大位移随着流冰速度的增大而增大；流冰速度在4.0 m/s时，明渠混凝土衬砌撞击区方向最大位移均出现最大“峰值”；流冰速度在4.0～5.0 m/s范围时，明渠混凝土衬砌撞击区方向最大位移随着流冰速度的增大而减小，说明流冰速度在0.5～4 m/s时，其刚性效果起主要作用，流冰速度在4～5 m/s时，其塑性效果其起主要作用。经曲线拟合后明渠混凝土衬砌撞击区方向最大位移随流冰速度的增大整体呈现出“单峰”现象，其变化在不同流冰压缩强度工况下均呈现出Pseudo-Voigt函数“峰值曲线”关系，不同压缩强度下流冰速度与方向最大位移的Pseudo-Voigt函数“峰值曲线”拟合关系如公式（10）所示，不同压缩强度下对应的公式（10）中的各项数值见表6。

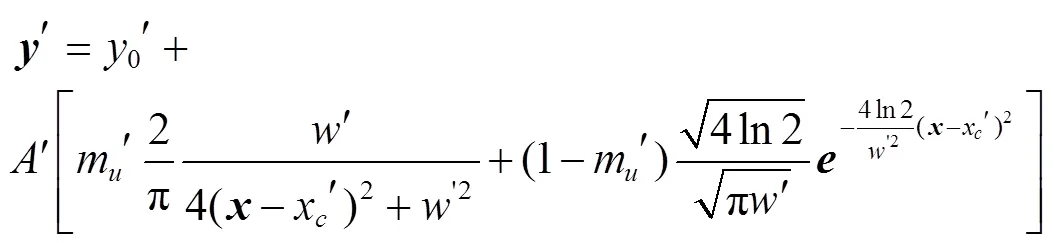
式中′为方向最大位移，m；0′为偏移量，Pa；′为面积，m2；′为半高宽，ns；x′为正中心；m′为剖面形状因子。

表6 不同压缩强度下对应拟合曲线中的各项数值

图7为最大等效应力拟合曲线残差图，由图可知，不同压缩强度下的残差数值均围绕残差值等于0的直线上下随机散布，可以看出残差的绝对值较小，均分布在0～0.8范围内，且不同流冰压缩强度对应的指数系数2均接近1.0，综合说明最大等效应力曲线拟合情况良好，论证了不同压缩强度下流冰速度与最大等效应力的Pseudo-Voigt函数“峰值曲线”关系合理。

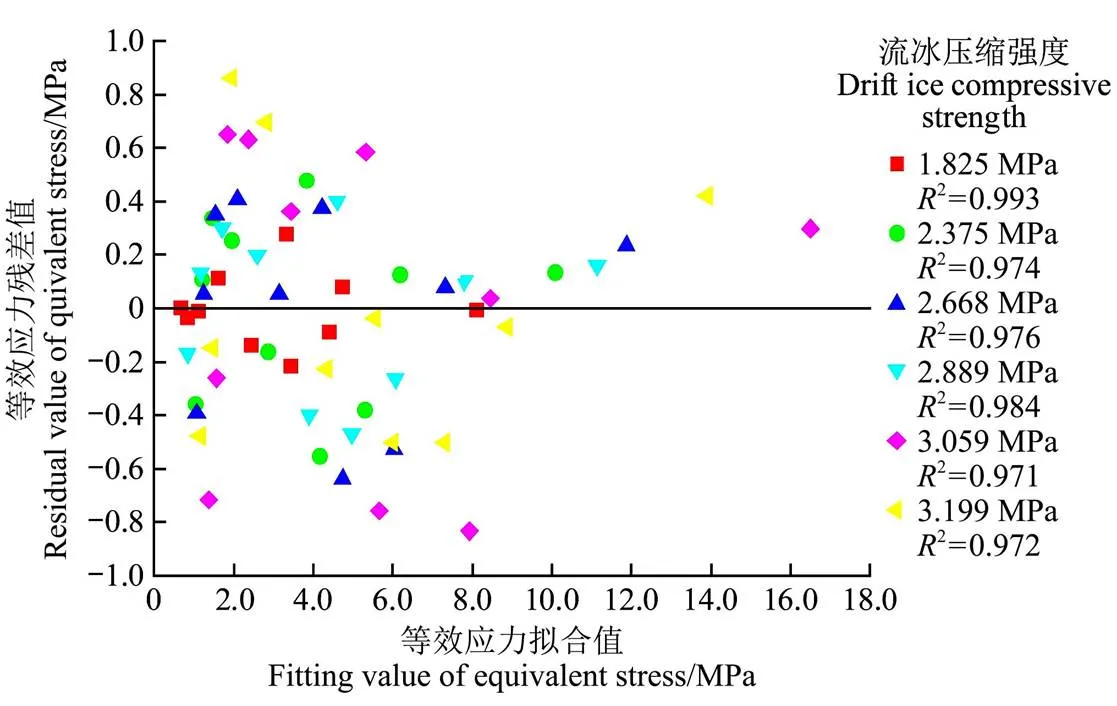
图7 最大等效应力拟合曲线残差图

图8为方向最大位移拟合曲线残差图，由图可知，不同压缩强度下的残差数值均围绕残差值等于0的直线上下随机散布，可以看出残差的绝对值较小，均分布在0～0.6范围内，且不同流冰压缩强度对应的指数系数2均接近1.0，综合说明方向最大位移曲线拟合情况良好，论证了不同压缩强度下流冰速度与方向最大位移的Pseudo-Voigt函数“峰值曲线”关系合理。

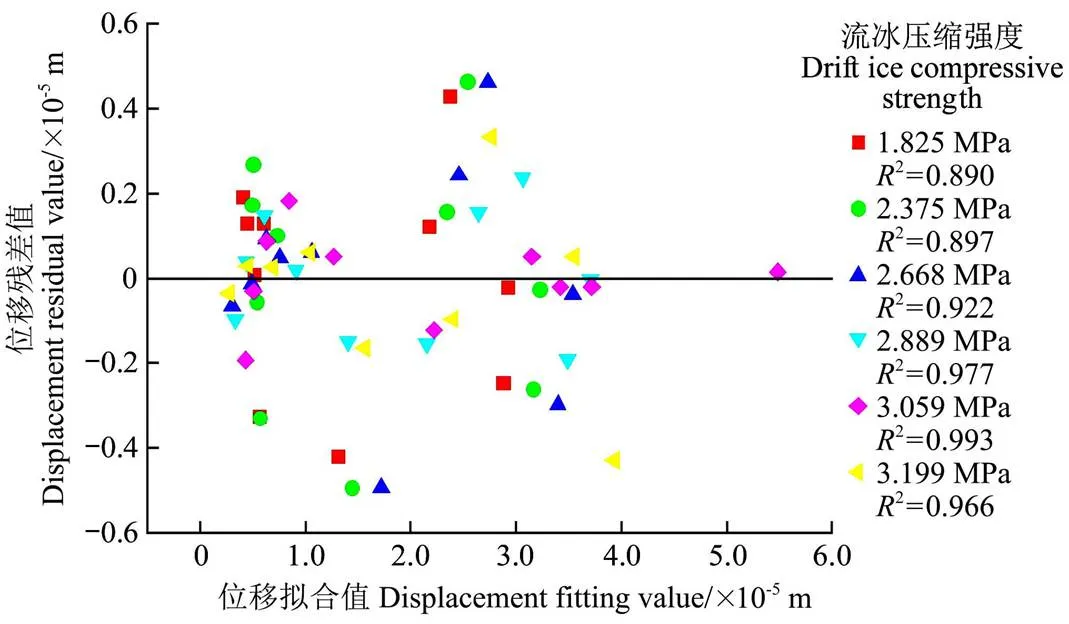
图8 X方向最大位移拟合曲线残差图

2.2.2 不同速度下流冰压缩强度对明渠衬砌的影响

由2.1节对最大等效应力、方向最大位移数据分析结果同理可知，流冰速度为4 m/s时，流冰压缩强度为1.825、2.375、2.668、2.899、3.059、3.199 MPa工况下对应的明渠碰撞区的方向最大位移分别为2.91×10-5、3.18×10-5、3.55×10-5、3.71×10-5、5.52×10-5、4.63×10-5m，所对应的最大等效应力分别为8.1×106、10.2×106、12.1×106、11.3×106、16.8×106、14.3×106Pa。分析不同流冰压缩强度与最大等效应力、方向最大位移的关系，绘制如图9、10所示拟合线关系图。

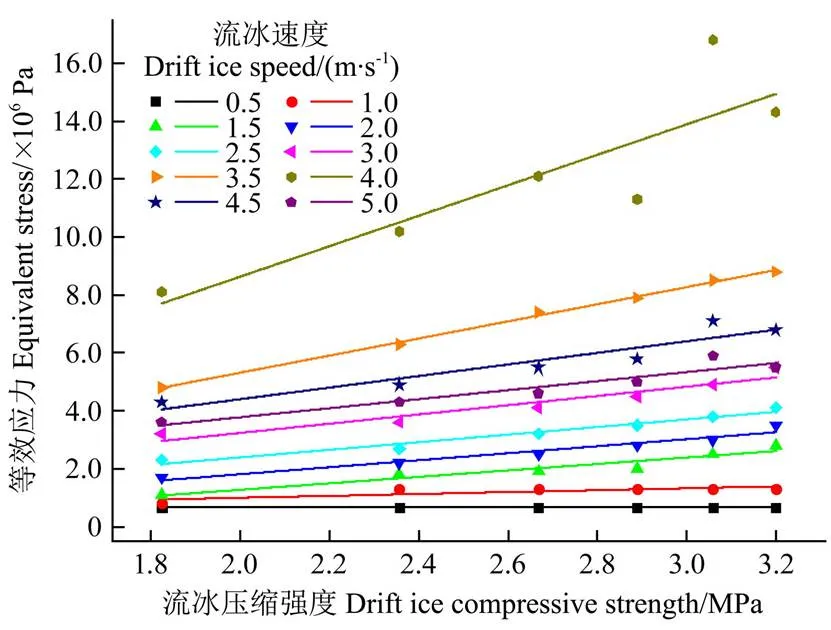
图9 流冰压缩强度与最大等效应力的关系

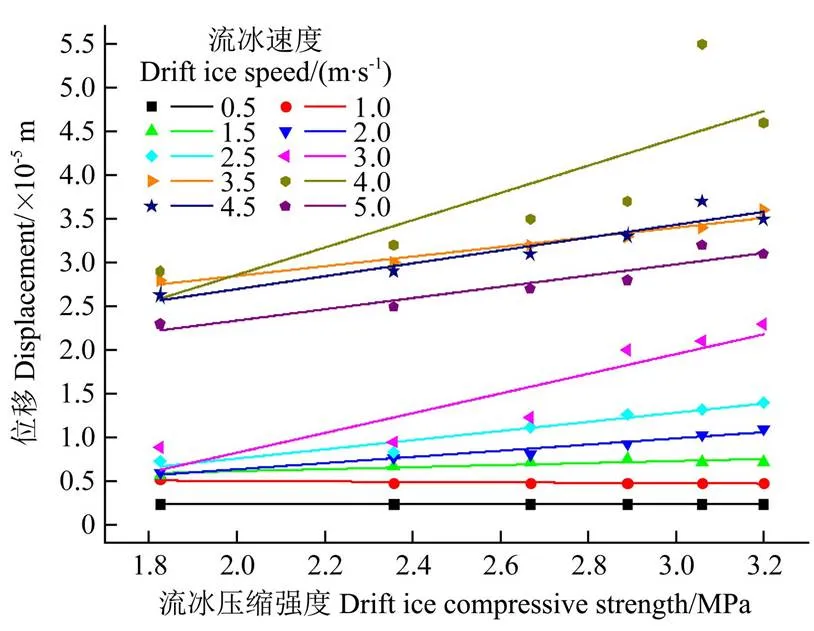
图10 流冰压缩强度与X方向最大位移的关系

由图9可以看出，在不改变流冰速度的情况下，只改变流冰压缩强度，流冰压缩强度对明渠混凝土衬砌撞击区的最大等效应力影响明显，其最大等效应力均随着流冰压缩强度的增大而呈现出近似线性增长的趋势。由表4可知温度越低，流冰压缩强度越大，因此，冰期输水需要考虑温度变化对流冰压缩强度的影响，减小运营期明渠输水过程中流冰对明渠衬砌的碰撞破坏作用。不同流速下流冰压缩强度与最大等效应力的线性拟合关系如公式（11）所示，不同流速工况下对应的公式（11）中的各项数值见表7。

=′+（11）

式中为最大等效应力，Pa；′为流冰压缩强度，MPa。

由图10可以看出，在不改变流冰速度的情况下，只改变流冰压缩强度，流冰压缩强度对明渠混凝土衬砌撞击区方向最大位移影响明显。其方向最大位移均随着流冰压缩强度的增大而增大，呈现出近似线性增长的关系。由表4知温度越低，流冰压缩强度越大，因此，冰期输水需要考虑温度变化对流冰压缩强度的影响，减小运营期明渠输水过程中流冰对明渠衬砌的碰撞破坏作用。不同流速下流冰压缩强度与方向最大位移的线性拟合关系如公式（12）所示，不同流速工况下对应的公式（12）中的各项数值见表8。

′=′′+′ （12）

式中′为方向最大位移，m。

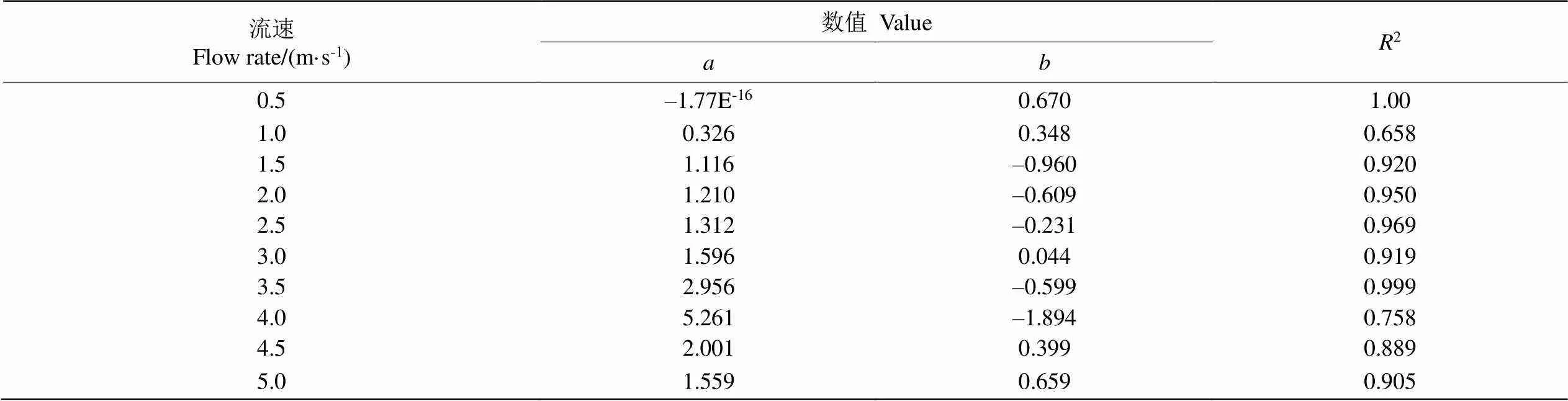
表7 不同流速工况下最大等效应力拟合曲线结果

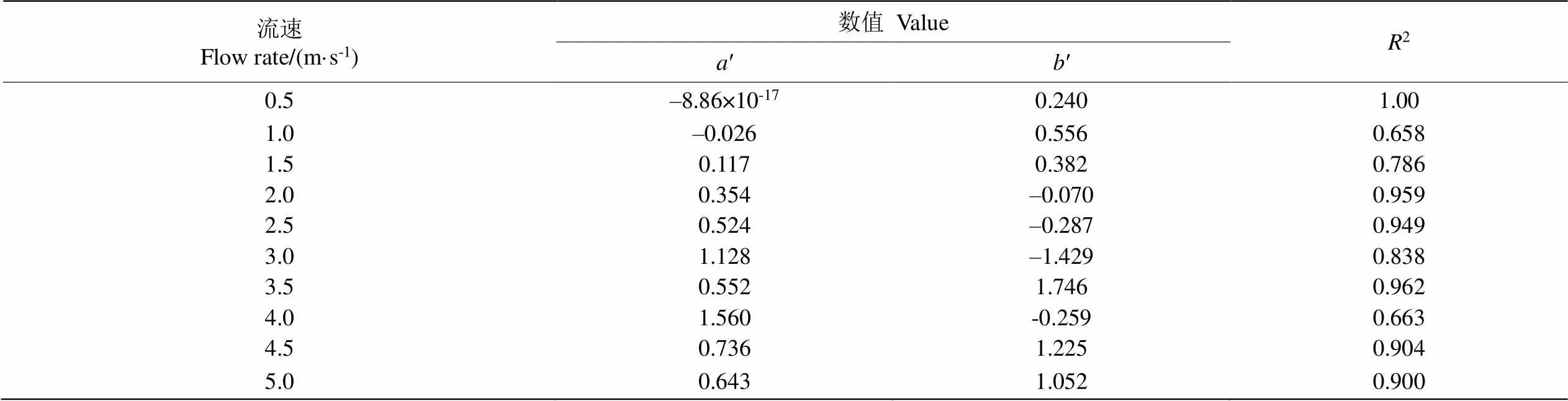
表8 不同流速工况下X方向最大位移拟合曲线结果

2.2.3 流冰不同速度与不同压缩强度组合工况对明渠混凝土衬砌的影响

通过上述对流冰速度与流冰压缩强度工况变化对明渠混凝土衬砌的单因素影响分析可知，最大等效应力以及方向最大位移均会受到流冰速度与流冰压缩强度因素的影响，且单因素的影响明显。为了综合分析两种单因素组合成多因素工况下对明渠衬砌的影响分析，通过Matlab软件建立流冰速度-压缩强度-最大等效应力关系图与流冰速度-压缩强度-方向最大位移关系图，如图11、12所示。

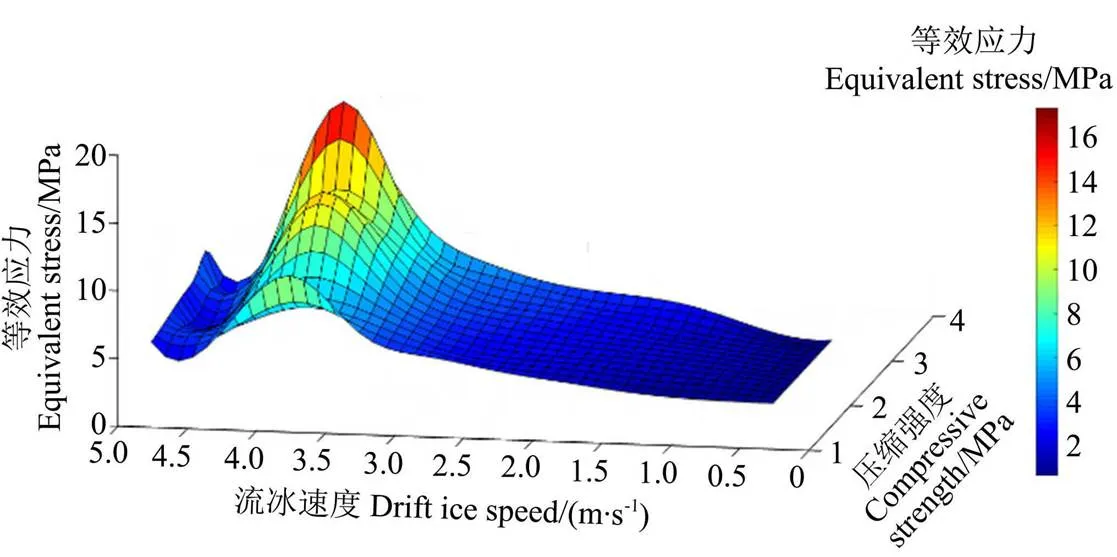
图11 流冰速度-压缩强度-最大等效应力关系图

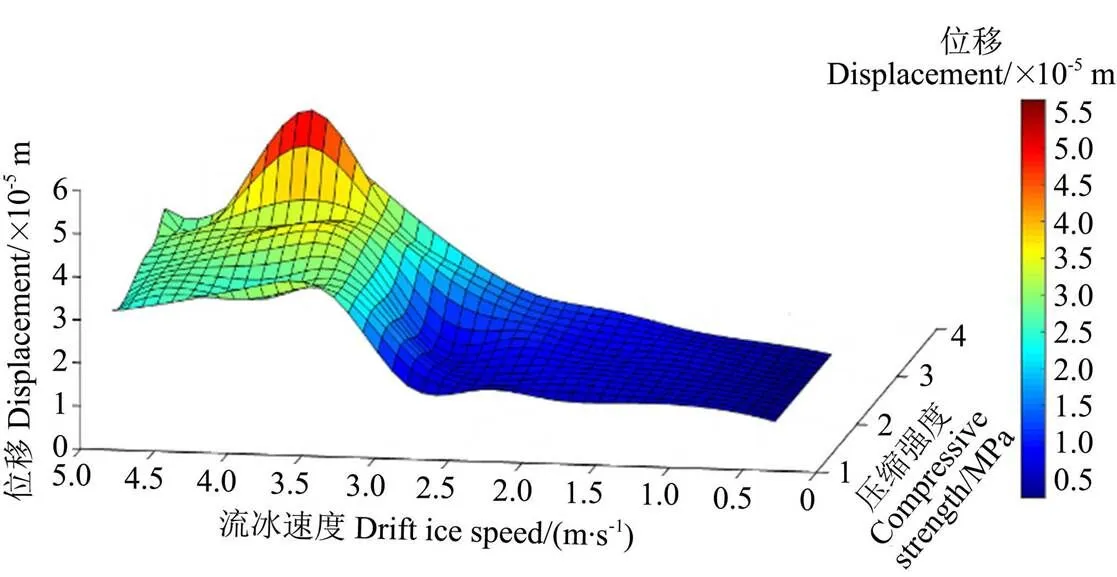
图12 流冰速度-压缩强度-X方向最大位移关系图

由图11可以看出流冰速度-压缩强度双因素组合工况中，流冰压缩强度为区间1.825～3.199 MPa情况下：当流冰速度在0.5～3.5 m/s区间时，其最大等效应力增长缓慢，增长变化率小但较为稳定；当流冰速度在3.5～ 4.0 m/s区间时，其最大等效应力有明显的增大，增长变化率较大；当流冰速度在4.0～5.0 m/s区间时，其最大等效应力有明显的减小，减小变化率较大；当流冰速度在0.5～5.0 m/s时，最大等效应力随着流冰速度的增大呈现增大后减小的趋势，且在4 m/s时变化率最为突出。流冰速度在0.5～3.5 m/s区间情况下，最大等效应力随着流冰压缩强度的增大而增大，但增长率较为缓慢，整体呈现出近似的线性关系。综合上述分析可认为，流冰速度对明渠撞击区最大等效应力的影响非常明显，但流冰压缩强度对明渠撞击区最大的等效应力的影响较为明显。由图11可以看出对明渠衬砌撞击区等效应力影响明显的组合工况区间为流冰压缩强度在1.825～3.199 MPa、速度在3.5～4.5 m/s时的组合情况，在其组合区间内等效应力变化范围为4.3～16.8 MPa，整体值大且增长变化幅度大；对明渠衬砌等效应力影响最大的双因素组合工况为流冰压缩强度是3.059 MPa、流冰速度是4.0 m/s的组合情况，其等效应力值为16.8 MPa，为所有工况的最大值，即双因素组合影响最大；对明渠衬砌影响较为不明显的组合区间为流冰速度在0.5～1.0 m/s、压缩强度在1.825～2.375 MPa时的组合情况，在其组合区间内等效应力变化范围为0.7～2.8 MPa，整体值小且增长变化幅度较为缓慢。

由图12可以看出流冰速度-压缩强度双因素组合工况中，流冰压缩强度为区间1.825～3.199 MPa时：当流冰速度在0.5～3.0 m/s范围内，其方向最大位移增长缓慢，增长变化率较小；当流冰速度在3.0～4.0 m/s范围内，其方向最大位移有明显的增幅，增长变化率较大；当流冰速度在4.0～5.0 m/s区间情况下，其最大等效应力有明显的减小，减小变化幅度较大；当流冰速度在0.5～ 5.0 m/s范围内，方向最大位移随着流冰速度的增大呈现出先增大后减小的趋势，整体增长变化幅度较为明显，方向最大位移最大等效应力在4 m/s时变化幅度最为突出。流冰速度在0.5～3.5 m/s区间情况下，最大等效应力随着流冰压缩强度的增大而增大，但增长幅度较为缓慢，整体呈现出近似的线性关系。综合上述分析可认为，流冰速度对明渠撞击区方向最大位移的影响非常明显，但流冰压缩强度对明渠撞击区方向最大位移的影响较为明显。由图12可以看出对明渠衬砌方向最大位移影响明显的组合工况区间为流冰压缩强度在1.825～ 3.199 MPa、流冰速度在3.5～4.5 m/s时的组合情况，在其组合区间内方向最大位移变化范围为2.59～5.52×10-5m，整体值大且增长变化幅度大；对明渠衬砌影响最大的方向最大位移双因素组合工况为流冰压缩强度是3.059 MPa、流冰速度是4 m/s的组合情况，其方向最大位移值为5.52×10-5m，为所有工况的最大值，即双因素组合影响最大；对明渠衬砌影响较为不明显的组合区间为流冰速度在0.5～1.0 m/s、压缩强度在1.825～2.375 MPa时的组合情况，在其组合区间内方向最大位移变化范围为0.24～0.52×10-5m，整体值小且增长变化幅度较为缓慢。

3 流冰对输水明渠撞击物理模型试验

3.1 试验方案设计与试验装置

本文通过室内模型试验研究流冰对输水明渠的碰撞作用，对数值模拟进行相应验证。室内试验模型与实际模型的几何比尺取为5,材料密度比尺为1.0，在常重力场条件下进行试验。

在模型试验中，以矩形水箱代替明渠模型，明渠衬砌采用C30混凝土板代替，流冰由动力装置牵引撞击明渠衬砌。其碰撞测试试验台与试验动力及数据采集分析系统图如图13所示。

3.2 试验设计

3.2.1 试验步骤

制备混凝土明渠模型，在混凝土衬砌上布置2个应变片，利用导线将应变片与动态应变测试分析系统采用半桥桥接方式连接；连接电脑与动态应变测试分析系统；启动计算机，在软件上设置好电压、混凝土弹性模量、泊松比等；将准备好的模型冰放入模型中，利用柔性连接将模型冰与牵引装置连接起来，启动电源，调节好脉冲发射器转速，随着模型冰碰撞明渠衬砌，读取明渠衬砌区域产生的动态应变曲线，保存处理数据；由应变时程曲线得到最大应变峰值，进而计算出应力与位移峰值。

3.2.2 试验工况

将准备好的大小规格同为0.2 m×0.2 m×0.1 m的模型冰进行试验，根据所模拟的不同流冰速度与不同流冰压缩强度工况，经相似比尺换算后对应的试验速度是0.224、0.447、0.671、0.894、1.118、1.341、1.565、1.789、2.012、2.236 m/s，对应的试验流冰压缩强度分别为0.365、 0.471 4、0.533 6、0.577 8、0.611 8、0.639 8 MPa，重复3.2.1节试验步骤并保存数据。

3.3 不同流冰速度对明渠衬砌的影响

由2.2.3节可知，对明渠衬砌影响最大的双因素组合为流冰压缩强度是3.059 MPa、流冰速度是4.0 m/s的组合情况,故选取流冰压缩强度为3.059 MPa不变、只改变流冰速度进行不同流速对明渠衬砌的试验验证。根据3.2节试验内容得到不同流冰速度工况下的最大等效应力峰值与方向最大位移峰值，对试验数据相似比尺换算后绘制不同流冰速度模拟与实验结果对比图，如图14所示。

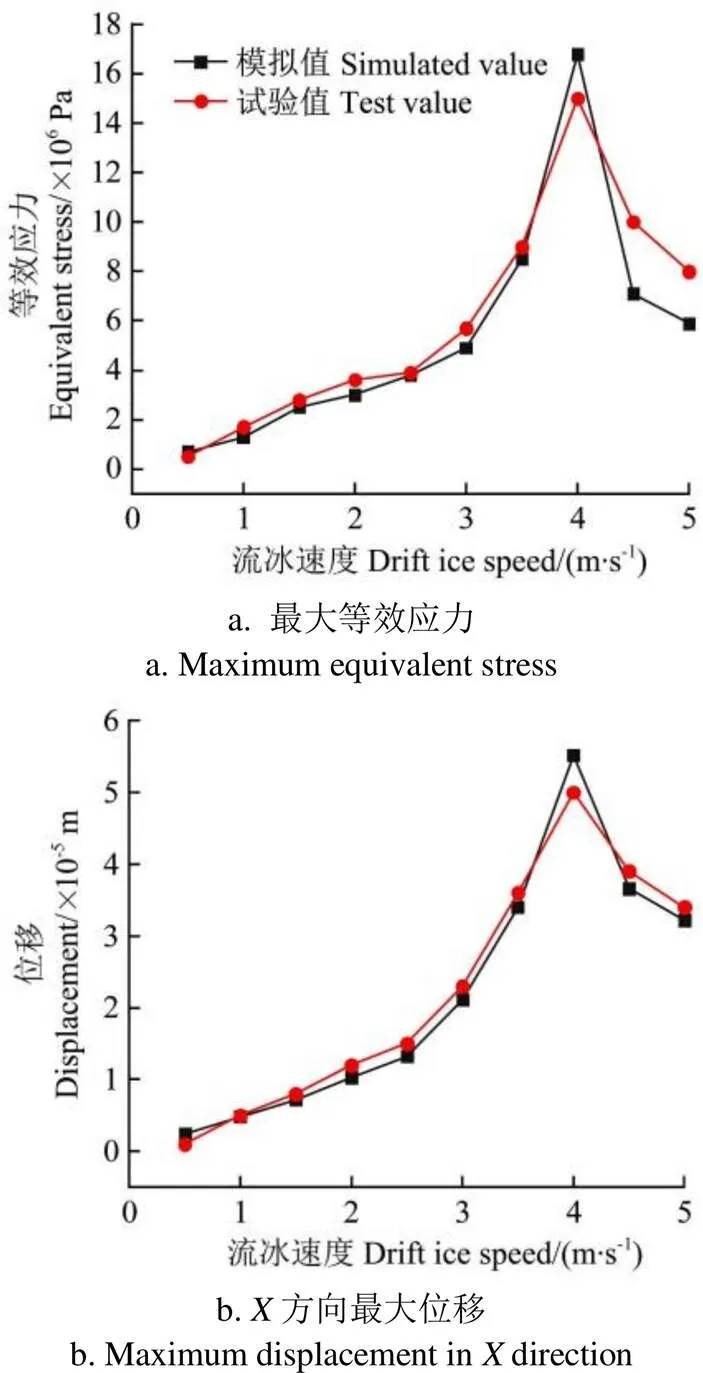
图14 不同流冰速度下模拟与试验结果对比

由图14可以发现，改变流冰速度，明渠撞击区的最大等效应力和方向最大位移的模拟值与试验结果有基本一致的趋势，趋势线吻合程度良好，均呈现出单峰现象，说明模拟结果真实可靠。还可以看出模拟值与试验结果存在一定的误差，可能与试验中水介质的扰动作用及二次碰撞有关。

3.4 不同流冰压缩强度对明渠衬砌的影响

由2.2.3节可知，对明渠衬砌影响最大的双因素组合为流冰压缩强度是3.059 MPa、流冰速度是4.0 m/s的组合情况,故选取流冰速度为4.0 m/s不变、只改变压缩强度进行不同压缩强度对明渠衬砌的试验验证。根据3.2节试验内容得到不同流冰压缩强度工况下的最大等效应力峰值与方向最大位移峰值，对试验数据相似比尺换算后绘制不同流冰压缩强度模拟与实验结果对比图，如图15所示。

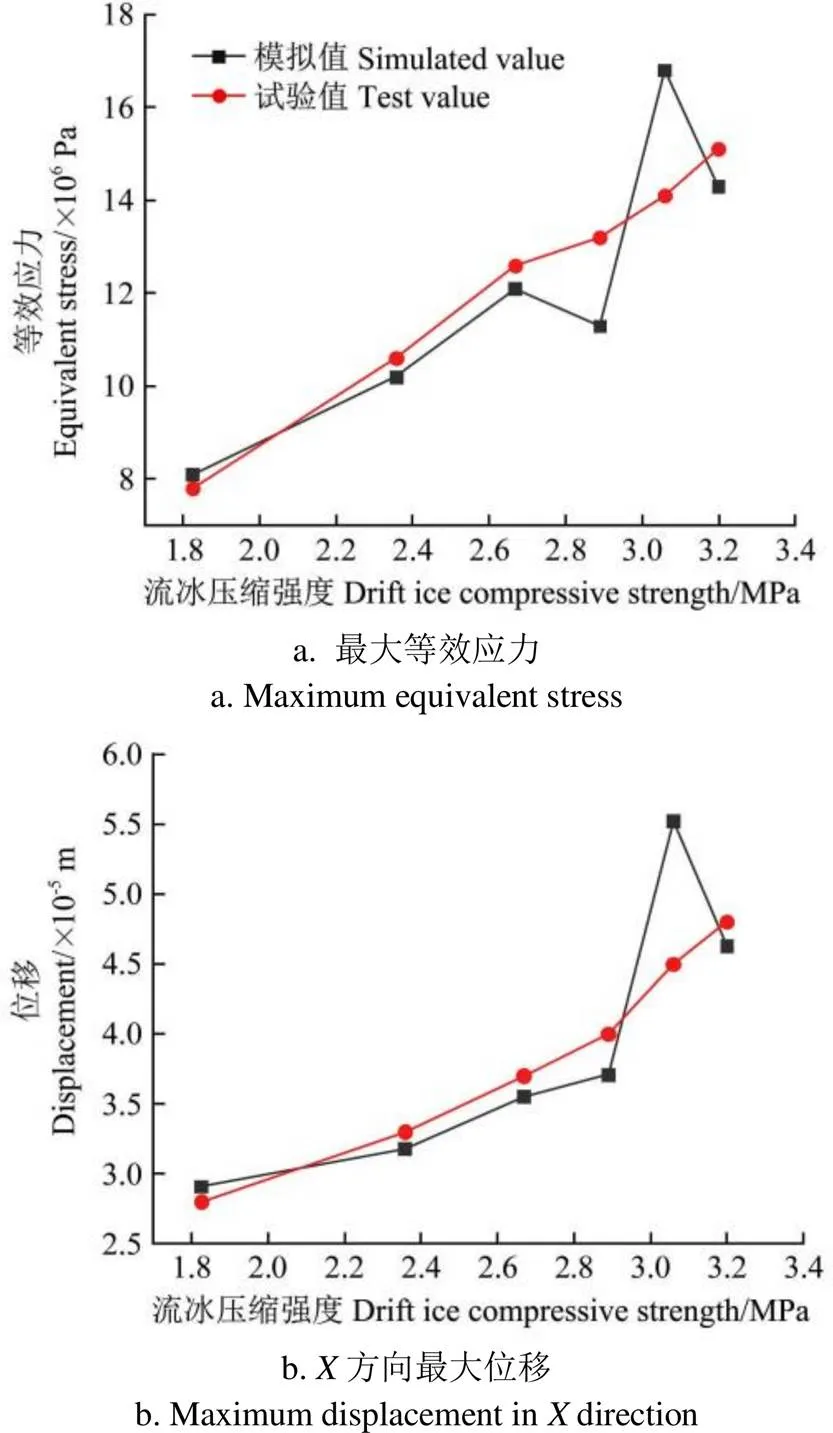
图15 不同流冰压缩强度下模拟与试验结果对比

由图15可以发现，改变流冰压缩强度，明渠撞击区的最大等效应力和方向最大位移的模拟值与试验结果有基本一致的趋势，吻合程度良好，均呈现出近似线性增长的现象，说明模拟结果真实可靠。还可以看出模拟值与试验结果存在一定的误差，可能与试验中水介质的扰动作用和二次碰撞有关。

4 结 论

本文主要考虑了水-空气-流冰三者耦合作用下对输水明渠混凝土衬砌碰撞影响研究，运用ANSYS/LS-DYNA有限元分析软件模拟流冰不同速度和不同压缩强度组合工况下对输水明渠衬砌的撞击影响过程，发现水-空气耦合介质中流冰碰撞输水明渠破坏规律，不考虑流冰二次碰撞因素，得到了以下结论：

1）在保持流冰压缩强度不变的情况下，只改变流冰速度，明渠撞击区最大等效应力与方向最大位移随着流冰速度的增大而先增大后减小，在4 m/s时整体均呈现出“单峰”现象，且均符合Pseudo-Voigt函数“峰值曲线”关系。说明流冰速度在0.5～4 m/s时，其刚性效果起主要作用，流冰速度在4～5 m/s时，其塑性效果其起主要作用。

2）在保持流冰速度不变的情况下，只改变流冰压缩强度，明渠撞击区最大等效应力与方向最大位移随着流冰压缩强度的增大而增大，均呈近似线性增长的关系。流冰压缩强度随着温度产生变化，温度越低，流冰压缩强度越大，因此，冰期输水需要考虑温度变化对流冰压缩强度的影响，减小运营期明渠输水过程中流冰对明渠衬砌的碰撞破坏作用。

3）综合分析所模拟的60种组合工况可以发现，在流冰压缩强度为1.825～3.199 MPa、流冰速度为3.5～ 4.5 m/s时的组合情况下，其等效应力值变化范围为4.3～16.8 MPa、方向最大位移值变化范围为2.59×10-5～5.52×10-5m，两者整体值大且增长变化幅度大，即组合工况对明渠衬砌撞击影响明显；在流冰压缩强度为 3.059 MPa、流冰速度为4.0 m/s的组合情况下，其等效应力值为16.8 MPa、方向最大位移值为5.52×10-5m，两者均分别为所有工况的最大值，即双因素组合对明渠衬砌影响最大；在流冰速度为0.5～1.0 m/s、压缩强度为1.825～2.375 MPa时的组合情况下，其等效应力变化范围为0.7～2.8 MPa、方向最大位移变化范围为0.24×10-5～0.52×10-5m，两者整体值小且增长变化幅度较为缓慢，即组合对明渠衬砌影响较为不明显。

实际工程中漂浮在水上的流冰其运动受多因素影响，如水流流态、流冰形状等；在模拟流冰碰撞明渠衬砌时，对于水介质中流冰体积、面积、厚度、碰撞角度等问题，还需要做进一步的研究。

[1] 杨开林.长距离输水水力控制的研究进展与前沿科学问题[J]. 水利学报，2016，47(3)：424-435.

Yang Kailing. Review and frontier scientific issues of hydraulic control for long distance water diversion[J].Journal of Hydraulic Engineering, 2016, 47(3): 424-435. (in Chinese with English abstract)

[2] Tuhkuri J. Analysis of ice fragmentation process from measured particle size distributions of crushed ice[J]. Coal Regions Science & Technology,1994, 23: 68-82.

[3] 蔡伟，朱凌，毕璐泽. 船-冰碰撞下冰材料有限元数值方法研究进展[J]. 船舶力学，2021，25(8)：1116-1126.

Cai Wei, Zhu Ling, Bi Luze. Review on development of finite element numerical method of ice material model under ship-ice collision[J]. Journal of Ship Mechanics, 2021, 25(8): 1116-1126. (in Chinese with English abstract)

[4] Sand B, Horrigmoe G. Finite element analysis of breaking ice forces on conical structures[C]. Proc. of the 4th International Symposium on Ice. Potsdam. 1998: 475- 482.

[5] 贡力，李雅娴，靳春玲. 流冰对引水隧洞撞击作用力学特性数值分析与验证[J]. 农业工程学报，2018，34(13)：144-151.

Gong Li, Li Yaxian, Jin Chunling.Numerical simulation and verification on impact damage mechanical property of drift ice on diversion tunnel[J].Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(13): 144-151. (in Chinese with English abstract)

[6] Rüdiger V B U P, Ehlers S. Model scale ice—Part B: Numerical model[J]. Cold Regions Science and Technology, 2013, 94: 53-60.

[7] 张宿峰. 流冰与桥墩的相互作用[D]. 哈尔滨：东北林业大学，2014.

Zhang Sufeng. Ice and the interaction of bridge piers[D]. Harbin: Northeast Forestry University, 2014. (in Chinese with English abstract)

[8] Zhang J M, Yuan Z G, Wu Y P. Analysis on the collision couple between drift ice and long-span prestressed concrete T-Rigid frame bridge pier[J]. Key Engineering Materials, 2015, 648: 17-24.

[9] 黄焱，郭晓辉，孙剑桥. 船-冰碰撞的模型试验方法研究[J].中国造船，2018，59(3)：46-59.

Huang Yan, Guo Xiaohui, Sun Jianqiao. Study on model test techniques of ship-ice impact[J]. Shipbuilding of China, 2018, 59(3): 46-59. (in Chinese with English abstract)

[10] Miryaha V A, Petrov I B. Discontinuous galerkin method for simulating an ice floe impact on a vertical cylindrical offshore structure[J]. Mathematical Models and Computer Simulations, 2019, 11(3): 400-414.

[11] 王健伟，邹早建.基于非线性有限元法的船舶-冰层碰撞结构响应研究[J]. 振动与冲击，2015，34(23)：125-130.

Wang Jianwei, Zou Zaojian. Ship's structural response during its collision with level ice based on nonlinear finite element method[J].Journal of Vibration and Shock, 2015, 34(23): 125-130. (in Chinese with English abstract)

[12] 赵海鸥. LS-DYNA动力分析指南[M]. 北京：兵器工业出版社，2003.

[13] Hallquist J O. LS-Dyna Theory manual[M]. Livermore Software Technology Cor-poration, California, 2006.

[14] 蒲兴富. 弹性体增强混凝土砌体墙爆炸响应的数值分析[D]. 宁波：宁波大学，2009.

Pu Xingfu. Numerical Analysis on Responses of Elastomer-Reinforced Concrete Masonry Walls Subjected to Blast[D]. Ningbo: Ningbo University, 2009. (in Chinese with English abstract)

[15] 徐国宾，李大冉，黄焱，等. 南水北调中线输水工程若干冰力学问题试验研究[J]. 水科学进展，2010，21(6)：808-815.

Xu Guobin, Li Daran, Huang Yan, et al. Laboratory study of problems in ice mechanics encountered in the Middle Route of South- to-North Water Transfer Project[J].Advances in Water Science, 2010, 21(6): 808-815. (in Chinese with English abstract)

[16] 杨亮，马骏. 冰介质下的船舶与海洋平台碰撞的数值仿真分析[J]. 中国海洋平台，2008，23(2)：29-33.

Yang Liang, Ma Jun. Numerical simulation analysis for the collision between offshore platform undre the sea ice medium[J].China Offshore Platform, 2008, 23(2): 29-33. (in Chinese with English abstract)

[17] 孟一，易伟建. 混凝土圆柱体试件在低速冲击下动力效应的研究[J]. 振动与冲击，2011，30(3)：205-210.

Meng Yi, Yi Jianwei. Dynamic behavior of concrete cylinder specimens under low velocity impact[J]. Journal of Vibration and Shock, 2011, 30(3): 205-210. (in Chinese with English abstract)

[18] 刘德良. 北极冰区船舶碎冰阻力数值仿真研究[D]. 大连：大连理工大学，2018.

Liu Deliang. Numerical Simulation of Crushed Ice Resistance of Ship in Arctic [J]. Dalian: Dalian University of Technology, 2018. (in Chinese with English abstract)

[19] 王鸿，贡力，王忠慧，等. 基于不同碰撞模型的流冰—输水隧洞碰撞动态响应研究[J].水资源与水工程学报，2021，32(1)：164-171.

Wang Hong, Gong Li, Wang Zhonghui, et al. Dynamic response of drift ice - water tunnel collision based on different collision models[J]. Journal of Water Resources and Water Engineering, 2021, 32(1): 164-171.

[20] 贡力，王鸿，杨轶群，等. 流冰对输水隧洞衬砌的撞击影响研究[J]. 振动与冲击，2021，40(4)：72-80.

Gong Li, Wang Hong, Yang Yiqun, et al. A study on the impact effect of drift ice on the lining of a water tunnel[J]. Journal of Vibration and Shock, 2021, 40(4): 72-80. (in Chinese with English abstract)

[21] 周政龙. 冬季运行中渠冰生消对输水明渠影响的研究[D].兰州：兰州交通大学，2018.

Zhou Zhenglong. Study on Influence of Channel Ice in Winter Operation on Water Diversion Channel[J]. Lanzhou: Lanzhou Jiaotong University, 2018. (in Chinese with English abstract)

[22] 王庆凯，张宝森，邓宇,等. 黄河冰单轴压缩强度的试验与影响因素探究[J]. 水利水电技术，2016，47(9)：90-94.

Wang Qingkai, Zhang Baosen, Deng Yu, et al. Study on test of uniaxial compressive strength of ice in Yellow River and its influencing factors[J].Water Resources and Hydropower Engineering, 2016, 47(9): 90-94. (in Chinese with English abstract)

Impact of drift ice on concrete lining of open water conveyance channel

Gong Li, Jia Zhiyuan, Li Yiqiang, Du Qiangye, Zhang Jiaoyan

(730070,)

Large blocks of drift ice have posed a strong impact on the open channels in the long-distance water delivery projects in the alpine regions. The drift ice is easy to form with the different speeds and compression strength in the high latitudes of northwestern China, especially the north of 35°N latitude. Particularly, the ice period lasts for 4 to 5 months in the cold and dry winter, covering from the freezing in November to the open in the following spring. The long-term collision of drift ice can cause some serious damage to the concrete lining of an open channel, such as cracking or peeling of the surface. The lining structure can result in different degrees of damage and deformation, even a threat to the long-term stability of water supply, including the safe operation of the open channel, irrigation of farmland, and water use for humans and animals. Therefore, this study aims to clarify the impact of the drift ice on the open delivery channels in the long-distance water delivery projects in the alpine regions. A collision model of the drift ice and open channels was also established as a water-air coupling medium using the ANSYS/LS-DYNA platform. Specifically, the collision motion equation of drift ice in the open channel was obtained, according to the display of time integration. The contact-collision process was assumed as a symmetric penalty function. The fluid-structure coupling calculation was then implemented considering the coupling effect between water-air-flow ice-open channels. After that, LS-DYNA SOLVER software was used to simulate the collision and extrusion of drift ice and open channel under different working conditions. As such, the degree of the collision was classified to evaluate the damage caused by the drift ice to the lining of the open channel. An indoor model test was carried out to verify the model. A damage law of drift ice was thus found in the water-air coupling medium when colliding with the open channel. The results showed that there was an approximate Pseudo-Voigt function peak curve relationship for the maximum equivalent stress and the maximum displacement in thedirection of the impact of the ice velocity on the open channel lining. Besides, there was an approximately linear relationship for the maximum equivalent stress and the maximum displacement in thedirection of the impact of drift ice compression strength on the lining of open channels. Furthermore, a combination interval posed a significant impact on the open channel lining, where the compressive strength of the flowing ice was 1.825-3.199 MPa, and the speed of the flowing ice was 3.5-4.5 m/s. This equivalent stress value of impact was 4.3-16.8 MPa, and the maximum displacement value in thedirection was 2.59×10-5-5.52×10-5 m. More importantly, a two-factor combination was posed the greatest impact on the open channel lining impact, where the flow ice compression strength of 3.059 MPa, and the flow ice velocity of 4.0 m/s. This equivalent stress value of impact was 16.8 MPa, and the maximum displacement value in thedirection was 5.52×10-5 m. By contrast, the combination interval presented a fewer outstanding impact on the open channel lining, where the drift ice velocity of 0.5-1.0 m/s, and the compressive strength was 1.825-2.375 MPa. This equivalent stress of impact was 0.7-2.8 MPa, and the maximum displacement in thedirection was 0.24×10-5-0.52×10-5 m. Therefore, there was a significant correlation between the temperature and the compressive strength of drift ice, while the flow velocity and the speed of drift ice. Correspondingly, the influence of the ice load needed to be considered in the design stage of the open channel lining structure. The findings can also provide sound theoretical and technical support to the safe operation of long-distance water transportation projects for the alpine regions in winter.

numerical simulation; test; fluid-solid coupling; drift ice; open channel; impact effect

10.11975/j.issn.1002-6819.2021.21.019

TV672

A

1002-6819(2021)-21-0163-10

贡力，贾治元，李义强，等. 流冰对输水明渠混凝土衬砌的撞击影响[J]. 农业工程学报，2021，37(21)：163-172.doi：10.11975/j.issn.1002-6819.2021.21.019 http://www.tcsae.org

Gong Li, Jia Zhiyuan, Li Yiqiang, et al. Impact of drift ice on concrete lining of open water conveyance channel[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(21): 163-172. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2021.21.019 http://www.tcsae.org

2021-08-03

2021-10-19

国家自然科学基金项目（51969011）；甘肃省科技计划资助项目（20JR10RA274, 21JR7RA301,20JR2RA002）

贡 力，博士，教授，研究方向为输水工程安全研究。Email: gongl@mail.lzjtu.cn