基于自适应gamma校正估计的图像去雾算法
吴正平,岑帅红
(三峡大学 电气与新能源学院,湖北 宜昌 201306)
1 引 言
雾、雾霾天气是我们生活中普遍的现象,它是由大气中所悬浮的小颗粒对光线发生一系列散射和吸收作用而产生的。雾、雾霾会造成户外拍摄的图像质量严重下降,比如:对比度降低、大量的细节信息丢失以及色调发生偏移等。图像质量下降会影响视觉系统的稳定性,使一些视觉系统的目标特征提取与识别等后续操作无法实现。因此,对图像进行去雾处理是非常有必要的,该方面的研究有非常重要的现实意义和广阔的应用前景[1]。
近年来,已经有许多学者对图像去雾进行了研究,这些研究主要围绕以下3大方面:
(1)基于图像增强的图像去雾方法。该方法主要通过增强图像的对比度,消弱或者增强图像中某些特定的信息来达到图像去雾的目的,其中包括一些基于Retinex的增强算法[2-3]。虽然上述方法在去雾方面取得了一定的效果,但是没有物理模型的支持,在一些图像上造成大量信息丢失,使复原的图像失真。
(2)基于大气散射模型的图像复原去雾方法。该方法根据一些先验知识,在大气散射模型的基础上,估算预测出图像去雾所需要的参数(透射率,大气光值等),然后再根据大气散射模型复原出去雾图像。其中包括He等人提出的经典暗通道去雾方法[4-5],该方法去雾效果较好,但在天空和景深突变区域有缺陷。这引发了许多学者进行研究,并提出了许多改进的暗通道去雾算法[6-8]。另外,Meng等人提出的边界约束图像复原方法[9],存在去雾过度,造成颜色失真等。Zhu等人提出的颜色衰减先验去雾方法[10],在浓雾场景下的去雾效果不好。
(3)基于深度学习的图像去雾方法。该方法通过建立一个网络模型,然后利用大量合成的图像数据进行训练,得到一个能够预测透射率或者直接得到去雾图像的网络模型。其中Cai等人提出的DehazeNet网络模型[11]通过预测透射率图进行去雾, Li等人提出的AOD网络模型[12]、Chen等人提出的混合残差学习网络模型[13]、Qu等人提出的EPDN网络模型[14]以及Dong等人提出的MSBDN-DFF网络模型[15]都是直接复原出去雾图像。该类方法受数据集的影响较大,不能适用所有场景下的雾图,对真实雾图去雾效果不理想,并且需要花费大量的时间进行训练,在硬件上也有要求。
综上所述,本文针对当前的图像去雾算法存在去雾不足、亮度偏暗以及去雾过度所造成的图像颜色失真等问题,提出一种新的透射率估算和改进大气光值估计的去雾方法。首先对于透射率的估算,通过像素级进行操作,避免出现块效应,即根据图像的亮度,利用具有衰减特性的不同gamma校正函数来拟合不同场景深度下有雾图像与无雾图像最小通道之间的关系,自适应估算出无雾图像最小通道,并通过引导滤波算法对估计的无雾图像最小通道进行修正,保持与有雾图像相同的结构,进而根据大气散射模型得到粗略的透射率。然后通过高斯相对性对透射率进行优化,得到结构保留,局部平滑的精确透射率;然而对于大气光值的估计,根据场景最深处往往存在图像的上方以及蓝色通道的像素值受场景深度影响最大等先验知识,对四叉树搜索算法进行改进,即通过增加搜索邻域,并把图像的蓝色通道的上半部分作为输入,稳定得到图像中场景最深处所对应的像素值作为大气光值。另外,由于复原图像偏暗,并利用gamma校正算法对复原图像的亮度通道进行增强。该算法的鲁棒性较强,计算时间较短,复原的图像明亮度适宜,景深突变处没有光晕效应,天空区域没有发生严重失真。
2 理论背景
2.1 大气散射模型
在图像去雾的方法中,基于大气散射模型复原的效果较好,利用该模型对图像进行复原的方法应用广泛。大气散射模型[16]是Narasimhan和Nayer等人在McCartney的基础上对雾天图像建立的数学模型,其数学表达式如式(1)所示:
I(x)=J(x)t(x)+A[1-t(x)],
(1)
式中:I(x)为有雾图像,J(x)是需要复原出的无雾图像,A是大气光值,t(x)为透射率,其具体表达式如式(2)所示:
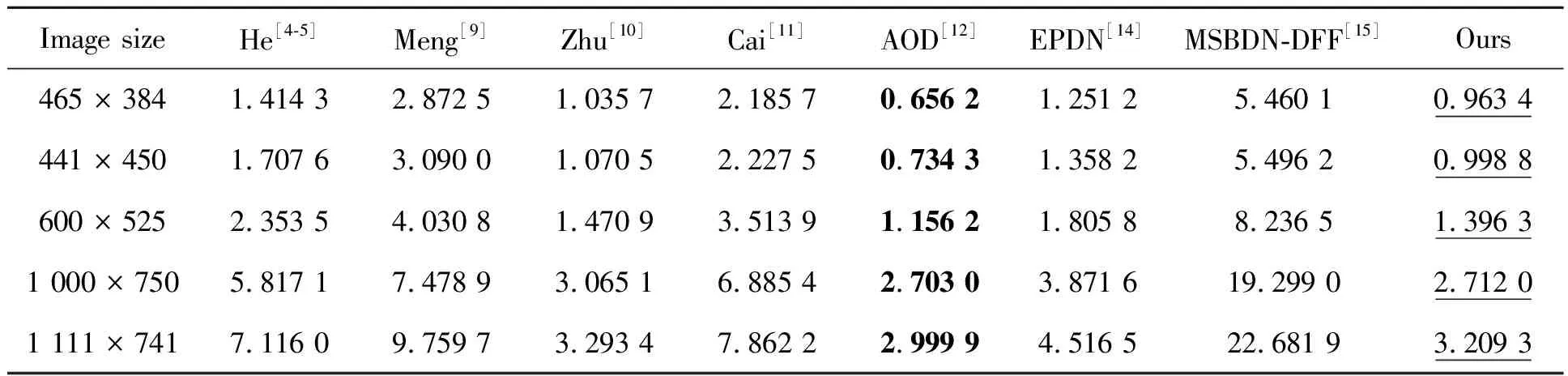
t(x)=exp[-βd(x)],0 (2) 式中:β为大气散射系数;d(x)为场景的深度,即成像设备到目标之间距离。另外,通过大气散射模型可以得到透射率t(x),其公式如式(3)所示: (3) gamma校正公式如式(4)所示: f(x)=xγ, (4) 式中:0≤x≤1。当γ>1时,f(x)≤x,因此该函数存在衰减的特性,在不同的γ下,gamma校正函数的示意图如图1所示。 图1 Gamma校正示意图 已知有雾图像和无雾图像之间也具有衰减特性,以及两者归一化值的关系示意图与gamma校正的示意图高度相似,由此可通过不同的gamma校正函数拟合一张图像中不同场景深度区域有雾图像与无雾图像之间的关系。 由于大气散射物理模型本质上是病态问题,可通过一些先验条件进行约束或通过对已知信息进行假设来获得所需信息,因此本文通过对大气散射模型以及gamma校正的分析可知,可利用不同的gamma校正函数来拟合不同场景深度下有雾图像和无雾图像的关系,即根据与场景深度呈正相关亮度通道,利用自适应gamma校正函数估算出无雾图像最小通道,并通过引导滤波算法对估计的无雾图像最小通道进行修正,保持与有雾图像最小通道具有相同的结构。进而根据式(3)得到初始透射率,最后通过高斯相对性优化初始透射率得到局部平滑的精确透射率。 3.1.1 自适应gamma校正估计无雾图像最小通道 根据大气散射模型式(1)可以推导出: (5) 由式(1)可知:斜率为1/t(x)=exp[βd(x)],与场景的深度有关;当I(x)/A=1时,J(x)/A=1;当J(x)/A=0时,I(x)/A=[1-t(x)];A、I(x)、J(x)三者的数值依次衰减。然而在一张图像中,不同区域场景深度d(x)不同,式(5)中的斜率1/t(x)与横轴上的截距[1-t(x)]不同,即I(x)/A和J(x)/A之间有着不同的关系,关系示意图如图2所示。 图2 I(x)/A与J(x)/A关系示意图 由于t(x)未知,式(5)无法进行求解,然而根据gamma校正示意图和I(x)/A与J(x)/A的关系示意图高度逼近,另外,已知随着场景深度的不断增加,式(5)中的斜率、截距不断增加,并且有雾图像的最小通道和亮度也不断增加,因此可根据有雾图像亮度,用不同的gamma校正函数来拟合图像中不同场景深度区域Imin/A与Jmin/A之间的关系。进而通过自适应gamma校正函数估计出无雾图像的最小通道,如式(6)所示: (6) 式中:S(x)>1;以及S(x)是与场景深度有关的函数,其公式如式(7)所示: S(x)=exp[V(x)]+b, (7) 式中:b=1.5时,去雾效果更好,是通过大量的实验获得。V(x)表示有雾图像在HSV空间中的明度通道值,该通道不受颜色的影响,与场景深度呈正相关的关系,因此利用该通道来估计场景的深度。 3.1.2 引导滤波算法修正无雾图像最小通道并获得初始透射率 已知有雾图像最小通道,可以通过式(6)估计得到粗略的复原图像最小通道。然而由于gamma校正函数是非线性函数,而在图像的局部区域,即场景深度相同区域,有雾图像最小通道与复原图像的最小通道是线性关系,可能会破坏复原图像最小通道的结构,因此本文利用He等人提出的引导滤波算法[5]来修正估计的复原图像最小通道,修正后的复原图像最小通道Jmin可表示为: Jmin(i)=akImin(i)+bk,∀i∈wk, (8) E(ak,bk)= (9) 式中:ε为正则化参数,防止ak过大。然后通过式(3)得到初始透射率,如下所示: (10) 式中:Imin为有雾图像的最小通道,Jmin为通过式(8)修正后估计得到的复原图像最小通道。 3.1.3 基于高斯相对性的透射率优化 已知图像局部区域内场景深度相同,透射率图应该在局部区域内平滑;然而图像中可能存在景深的突变,透射率随之发生突变,透射率图存在大尺度的结构,因此需要保留透射率中大尺度的结构,平滑掉小尺度的纹理。基于此,本文通过一种新的尺度度量的方法——高斯相对性[17]对透射率进行优化,该方法在不破坏图像结构的情况下有效地定位并消除局部纹理,优化效果图如图3所示。平滑优化函数如式(11)所示: 图3 透射率优化前后对比图 (11) 大气光值是大气散射模型中一个重要的参数,它决定着复原图像的亮度。由大气散射模型可知,当d(x)→∞时,t(x)=0,得到I(x)=A,因此找到图像中场景最深处,即可得到大气光值。对于该方面的研究并不是太多,其中包括 Kim等人提出的基于四叉树搜索的大气光估计方法[18],但该方法会受到近景区域平滑白色物体影响,以及景深最远区域中前景物体的影响,造成大气光值估计错误,如图4所示。 图4 大气光估计效果对比图 为了得到更加精确的大气光值,本文对四叉树搜索算法进行了改进。首先根据图像中场景最深处的背景区域往往在图像的上半部分,以及有雾图像中蓝色通道像素值受场景深度的影响最大,因此将有雾图像的蓝色通道上半部分作为输入,并增加输入图像上半部分的搜索领域;另外,最远处所在的区域会存在前景物体的影响,造成场景最深处区域标准差过大,使区域定位错误,该问题可以通过降低区域标准差的比例来解决。利用式(12)作为图像中最远位置的评判标准: c(i)=Imean(i)-aIstd(i),i=1,2,…,5, (12) 式中:a=0.3,该值是经验值,可以通过大量的实验获得;Imean(i)、Istd(i)为搜索区域i的平均值和标准差。经实验验证,本方法可以精确地搜索到有雾图像中场景最深处所在的位置,如图4所示,即可得到较为精确的大气光值。该算法所得到的大气光值使复原图像的亮度更加适宜,花费时间更短。算法步骤如下所示: (1)输入有雾图像中蓝色通道图像的上半部分; (2)把图像分成5个区域,如图5所示; 图5 分割区域图 (3)根据式(12)计算出每一个区域的数值; (4)选取对应最大数值的区域。并返回到第1步;直到搜索区域尺寸小于规定值; (5)把最后搜索区域所对应的有雾图像中各通道最大值作为大气光值。 通过第一节中经过高斯相对性优化后所获得的精确透射率T(x),以及第二节中经过改进后的四叉树搜索算法所获得的大气光值A,根据大气散射模型(1),即可复原出无雾图像,公式如式(13)所示: (13) 为了使复原图像具有更好的视觉效果,另外通过gamma校正算法对复原图像的亮度图像(V)进行增强,其公式如式(14)所示: (14) 为了验证本文所提算法的有效性与优越性,本文通过主观比较与客观比较两方面进行验证,分别通过与多种经典的传统图像去雾算法和近年来的基于深度学习的图像去雾算法进行对比,充分证明该算法的有效性与优越性,使算法更加具有说服力。 主观评价主要是通过人眼直接观察的视觉效果进行评价,没有理论的支持,具有一定的局限性,但在一定程度上能够说明图像质量的好坏,并且能够快速评定图像的质量。因此通过5种不同类型场景的真实自然雾图,即含有天空区域的薄雾图像,含有明亮区域的浓雾图像,含有天空区域的浓雾图像,未含有天空区域的薄雾图像,含有白色物体的浓雾图像,首先分别与He等人[4-5]、Meng 等人[9]、Zhu等人[10]提出的3种经典传统去雾算法进行主观比较,效果对比图如图6所示。从图6(b)可以看出He等人提出的算法得到的效果图在景深突变区域产生光晕效应,以及场景深处去雾不彻底。从图6(c)可以看出Meng等人提出的算法在损失图像色彩情况下,对图像进行去雾,然而造成去雾过度,使复原图像的天空区域色彩发生偏移,造成图像发生严重失真。从图6(d)可以看出Zhu等人提出的去雾算法适用性不强,浓雾场景下去雾不彻底,大气光值估计偏高,造成复原图像偏暗,视觉效果不自然。然而从图6(e)可以看出本文算法的效果图明亮度适宜,景深突变处没有光晕效应,以及图像没有发生严重的失真,视觉效果自然,因此本文算法的去雾图像有较好的主观视觉效果。另外,通过与近些年基于深度学习的4种图像去雾算法进行主观比较,如图7所示。从图7(b)可以看出DehazeNet网络模型[11]复原出的图像在近景区域偏暗,远景区域去雾不彻底;从图7(c)可以看出AOD网络模型[12]复原出的图像与DehazeNet网络模型一样,近景区域偏暗,远景区域去雾不彻底;从图7(d)可以看出EPDN网络模型[14]在浓雾场景下,去雾效果不好,留下有残雾;从图7(e)可以看出MSBDN-DFF网络模型[15]对真实自然雾图的去雾效果较差,该算法的鲁棒性不强;从图7(f)可以看出,本文算法鲁棒性更强,复原的图像明亮度适宜,去雾更加彻底,因此对于真实雾图,该算法比基于深度学习的去雾算法复原图像的主观视觉效果更好,表明该算法比其他算法的复原图像在主观视觉效果上有优势。 图6 不同传统去雾算法处理的5种不同类型场景真实雾图的去雾效果对比图 图7 不同深度学习算法处理的5种不同类型场景真实雾图的去雾效果对比图 本文采用通用的4种无参考客观评价指标[19]:对比度(C)、信息熵(IE)、平均梯度(AG)以及运行时间(T),分别与He等人、Meng等人、Zhu等人提出的3种传统去雾算法,以及4种基于深度学习的图像去雾算法进行比较,各种指标结果对比如表1~4所示。其中对比度、信息熵、平均梯度的值越高越好。从表1和表2可以看出本文算法比He等人、Meng等人、Zhu等人提出的传统去雾算法以及所有基于深度学习的去雾算法所复原出的图像平均梯度和对比度都更高,因此本文算法比它们7种算法的图像去雾效果更好,复原图像更加清晰,在景深突变处没有光晕效应,天空区域没有发生严重失真。然而从表3可以看出本文算法复原出的部分图像信息熵在这8种算法中不是最高的,但大部分都能排到第二和第三位,具有较高的值,因此复原图像的信息较为丰富,没有发生严重失真。另外,从表4可以看出算法的运行时间是较短的,比其他3种传统去雾算法的运行时间都短,并且相比于基于深度学习的大部分去雾算法的运行时间较短,只比AOD网络模型的运行时间略长,从以上综合考虑,该算法复原图像具有不错的客观指标。因此该算法的图像去雾效果较好。 表4 各算法的运行时间 本文提出了一种自适应gamma校正估计的图像去雾算法。首先为了避免出现块效应,通过像素级操作对透射率进行估算,即根据与场景深度相关的图像亮度,利用不同的gamma校正衰减函数来逼近图像中不同场景深度下有雾图像与无雾图像之间的关系,进而自适应估算出无雾图像最小通道,并通过引导滤波算法对无雾图像最小通道进行修正,保持与有雾图像最小通道具有相同的结构。然后通过高斯相对性平滑初始透射率的局部纹理,并不破坏其结构。另外,对于大气光值的估计,通过增加搜索领域,将有雾图像中蓝色通道上半部分作为输入的改进四叉树算法,精确获得有雾图像中场景最深处所对应的像素值作为大气光值。最后利用gamma校正算法对复原图像的亮度进行增强。通过实验验证,本文提出的假设成立,实验结果表明复原图像的对比度和平均梯度分别提高40.66%,20.98%,运行时间相比于传统算法中运行时间最短的算法,缩短了6.57%,以及复原图像不存在光晕效应,并且在图像不发生严重失真的前提下,去雾更加彻底,明亮度适宜,视觉效果自然。2.2 gamma校正
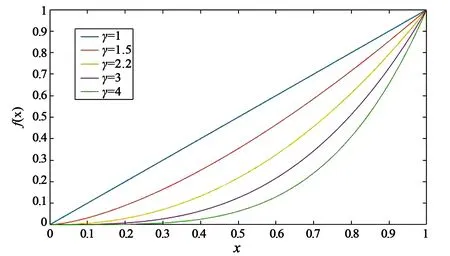
3 自适应gamma校正估计的图像去雾算法
3.1 透射率估计
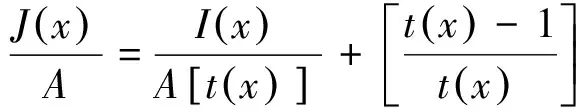
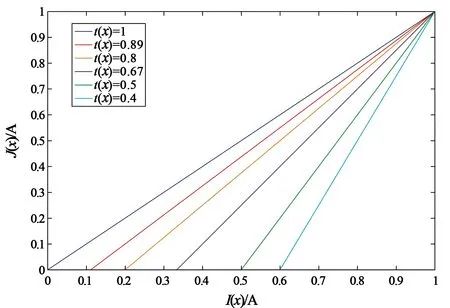
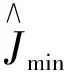
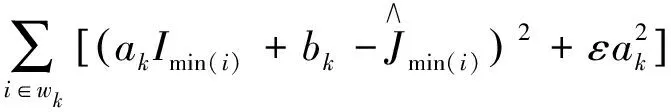



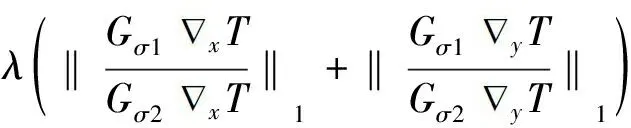
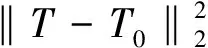
3.2 大气光估计


3.3 图像复原与增强
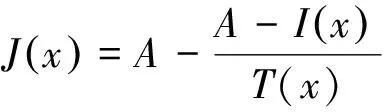
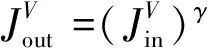
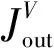
4 实验结果与比较
4.1 主观比较


4.2 客观比较
5 结 论

