提升数学素养，源于教学课堂——以苏科版八年级下册第11章反比例函数的图象与性质为例

◎康 聪

(苏州高新区实验初级中学，江苏 苏州 215000)

数学素养属于认识论和方法论的综合性思维形式，它具有概念化、抽象化、模式化的认识特征.具有数学素养的人善于把数学中的概念结论和处理方法推广应用于认识一切客观事物.数学素养的培养源于课堂，因此，教师的引导要注重知识的发生、发展过程，从一般到特殊，从简单到复杂.基于此，笔者试以“反比例函数的图象和性质1”为例，对核心素养的培育进行剖析.

一、复习回顾

师：我们在画一次函数的图象的时候，主要经历了哪些步骤？

生1:列表、描点、连线.

生2：学习一次函数的过程是概念、图象与性质和应用.

师：好的，借助函数图象，我们研究了性质(PPT展示一次函数的学习路径).

师：我们举一个一次函数的例子：y=2x+1，谁来说一说它的性质？

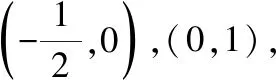
师：很好，我们通过画一次函数的图象，确定了函数的性质.借助这样的经验，我们继续踏上新的学习旅程，昨天我们学习了反比例函数，现在我们来看这样的问题.

设计目的：学习过程注重数与形的结合，动态生成学习情境，学生通过形的特点引出一次函数的性质.“函数”是我们已经掌握的一种数学模型，学生在已有的知识生长点，探究反比例函数的学习方式.

二、新课引入

(一)初探：猜想、验证

板书呈现：

生：x≠0，因为x=0时分式无意义.

师：x≠0，说明函数图象与y轴无交点.那么y的值可以等于0吗？

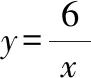
师：既然x，y取不到0，那么这个函数图象在平面直角坐标系中会有什么特点呢？

生：分成两部分：当x>0时，y>0；当x<0时，y<0.

师：具体说说，怎么得到的呢？

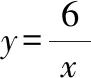
师点评：很好，这样确定了图象在第一、三象限，还有其他内容吗？

生：当x>0时，y随x的增大而减小；当x<0时，y随x的增大而减小.

师：谁能把这个变化趋势具体化？

生：当x>0时，如，x=2，y=3；x=6，y=1.此时y随x的增大而减小.

当x<0时，如，x=-1，y=-6；x=-2，y=-3.此时y随x的增大而增大.

所以要分成两部分说明反比例函数图象的分布区域.

师：如果不讨论x的范围，那么变化趋势相同吗？

生：不同，如，当x=2，y=3，当x=-1，y=-6，此时y随x的减小而减小，与刚才的推理不符.

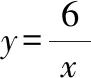
设计目的：问题是数学的心脏，是思维的起点.学生通过发现问题、解决问题的过程，能由数想形，自主建构学习内容，突破反比例函数的重点内容，进而发挥主观能动性，获得探求新知识的智力价值和智慧价值.

(二)再探：列表、交流

(教师观察学生的作图情况，并展示学生的作图成果)

师：我们一起来看画好的图象，并进行一一验证.

①第一、三象限；

②与坐标轴没有交点；

③当x>0与x<0时，y都随x的增大而减小.

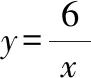
第一步，列表.

师：在表格中，我们怎样取值比较好呢？取值需要注意什么事项呢？

生1：取整数，这样计算方便.

生2：正负数都要取.

生3：多取点，这样画图精确.

师：根据刚才大家的反馈，我们在列表时，自变量x的取值要注意以下几点(PPT)：

(1)在自变量取值范围内取值；(x≠0)

(2)一定要有代表性；(兼顾正、负)

(3)大小要适度；(描点时好操作)

(4)要尽量多取一些数值.

师：通过表格，你准备取哪些值呢？

xy=6x

生：从小到大取，可以取-6，-4，-3，-2，-1,1,2,3,4,6，等等.

教师填写数据，展示学生画图的成果.

第二步，描点，连线.

师：两点之间，是线段还是曲线呢？

生：如果是直线，那么应该是一次函数，我们可以在反比例函数图象上任取一个点，来验证它是否在这条直线上.

生：取(1.2,5).

教师在几何画板演示，发现点(1.2,5)在曲线的下方.

师：这说明我们构造的整数点之间的连线，不是直线.把自变量范围内的点进行细化，随着点数的增加，构造图象的点越来越密，几何画板充分展现了反比例函数图象中的两支曲线的生成过程，学生经历了曲线的产生过程，并由此理解反比例函数是曲线，为高中学习微积分知识做好铺垫.

教师展示反比例函数的图象.

师：借助图象，我们继续来研究反比例函数的性质.

生：有两条曲线.

师：这两条曲线又叫双曲线.那么，双曲线有什么性质呢？

生：增减性：当x>0时，y随x的增大而减小；当x<0时，y随x的增大而减小.

师：很好，强调了双曲线的增减性要分成两个象限，这是一个非常重要的内容(板书).

归纳(板书)：当k>0时：

(1)函数图象分别位于第________象限.

(2)在第________象限，y随x的增大而________.

设计目的：推理是数学知识形成的重要手段，学生通过猜想反比例函数的图象及性质，画出图象的轮廓，再验证猜想的过程，进而达到在思辨中内化知识，拓展思维能力的目的.

(三)三探：完善、展示

归纳(板书)：当k<0时：

(1)函数的图象分别位于第________象限；

(2)在第________象限，y随x的增大而________.

师：通过画图情况，我们知道点与点之间用光滑的曲线连接，那么在自变量x靠近0的部分，如果k>0，函数值y会有怎样的特点呢？

生：当x>0时，图象无限靠近y轴正半轴，x越小，y的取值越大.同样地，当x<0时，图象无限靠近y轴负半轴，x越大，y值越小.

师：类似地，当x取无穷大时，y值有怎样的对应情况呢？

生(齐说)：y值趋于0.

师(完善曲线)：无限接近x，y轴，但不与x，y轴相交，这就是渐近性.这样，我们就得到了反比例函数图象向坐标轴无限靠近的性质.

设计目的：学生用类比的思想得到反比例函数(k<0)的图象与性质，并用文字语言归纳概括，水到渠成.

(四)归纳总结

师：请同学们回顾，本节课你有什么收获呢？

生1：学习了反比例函数的图象和性质.

生2：在探究函数的性质时，学到了一些解决问题的策略：实例—猜想—验证—归纳.

师点评：很好，学习数学不但能扩大我们的知识领域，更重要的是能提高我们解决问题的能力，这就是数学素养的魅力！

师：通过一次函数的学习生长点，我们进行以下学习方式：

设计目的：注重培养学生的开放、灵活、自信、专注、合作等良好品质和独立思考能力.本节课整体的课程设计都采用自主探究的学习方式，学生在感悟获取知识的同时，经历知识的生成和推导的过程，并在这一过程中感悟数学思想，提升数学核心素养.

(五)教学思考

数学概念获得的过程是典型的数学抽象的过程，教师在教学过程中应尽可能地创设适合学生的问题情境，设计对概念的概括与提炼更加精准的学习活动，凸显概念的“再创造”的过程.波利亚认为：“学东西最好的途径是亲自去发现它.”学生已经学习过一次函数，可以在已有的学习经验中自主探索反比例函数的图象和性质，另外，教师要围绕教学目标进行深度探索，运用探究式教学，实现学生对数学知识和方法的深刻理解的目的.

注重知识的外延有利于核心素养的衔接.反比例函数的图象是曲线，学生通过解析式具体分析，可以判断图象不能是直线，并验证成功；教师通过几何画板，构造连线过程，进而说明反比例函数图象是曲线的缘由.渐近性刻画了函数的极限思想，当x趋于无穷大时，y趋于0，这为高等数学极限学习打下基础，从感性认识到理性探究，为培养学生直观想象、抽象素养、逻辑推理素养创造条件.这有利于学生积累用数学思维思考问题的经验，进而提升逻辑推理素养.

学生的核心素养和关键能力的培养，对课堂的品质要求越来越高，而学生的思维培养具有长期性.因此，教师在课程整体结构设计中，要以学生的学习能力和素养为育人目标，在知识脉络上协调数学知识、方法、思想、能力及素养等各个要素之间的关系，从而达到新旧知识的关联、建立数学各分支的内在联系，及数学思想方法连贯性的统一要求.