基于回归Kriging代理模型的吸油烟机用多翼离心风机优化
诸永定,肖千豪,吴灵辉,王军*
(1. 浙江省健康智慧厨房系统集成重点实验室,浙江 宁波 315300;2.华中科技大学能源与动力工程学院,湖北 武汉 430074)
多翼离心风机因流量系数大、尺寸小和低噪声等优点广泛应用于吸油烟机、空调、热水器等家用电器和各种通风换气场合中.多翼离心风机典型特征在于叶片出口角大(强前向叶片)、叶片数众多(多达60片)、叶道短,风机内部存在严重的流动分离、泄露和跨叶轮流动[1]等复杂流动现象,导致油烟机最高效率不足50%.在不同油烟机产品开发中,由于其内部流道结构差异化,导致风道设计匹配合理性得到重视.在油烟机发展过程中,基于高可信度计算流体力学的气动分析与优化方法在提高油烟机排烟、效率等性能、降低研究成本等方面发挥着越来越重要的作用.由于油烟机复杂的腔体结构和油烟机内置风机复杂的三维流动,需要消耗大量计算资源,加上追求油烟机更高的综合性能,还需要大量CFD计算去获取最优设计参数.
YANG等[2]利用改进非支配排序遗传算法(NSGA)对4个设计参数的多翼离心风机进行优化,在30代之后获得最终优化方案.这种启发式优化方法,如遗传算法[3]和粒子种群算法[4]等,虽然具有良好的全局搜索能力,但需要大量迭代计算.在考虑计算成本时,很难在油烟机等工程应用中采用.为提高油烟机优化效率,同时兼顾全局搜索能力,文中采用一种基于代理模型的优化方法.代理模型是指在优化设计过程中可以代替复杂且费时的数值分析模型的数学模型.常见代理模型算法有Kriging模型[5]、神经网络[6]、多项式响应面[7]和支持向量回归[8]等.文献[9]指出,代理模型的建模过程,实质上是采用了机器学习技术,从少量样本信息中学习出目标函数和约束函数对设计变量的规律或知识,因此代理模型可以看作是针对小样本的监督式机器学习模型.代理模型在多翼离心风机工程应用优化过程中扮演着重要的角色.文献[10]在尺寸限制下的蜗壳型线设计方法中,利用径向基(RBF)神经网络构建准确度较高的代理模型对设计参数进行优化.由于CFD与真实性能相比,总会有一定的误差,而上述提到的Kriging模型、RBF神经网络等,均未考虑误差影响.
为消除误差对代理模型优化结果的影响,同时避免出现过度拟合的情况,文中利用回归Kriging模型作为代理模型,对油烟机用多翼离心风机的气动性能进行优化.
1 研究对象
图1为某吸油烟机结构示意图.油烟从油烟机腔体中沿竖直方向被吸入,经过过滤网后经集流器整流沿叶轮轴向进入风机内部,然后径向流入叶轮.油烟经叶轮做功后动能增加,甩出叶轮进入蜗壳,经蜗壳将油烟动能转化为静压并通过出风罩流向油烟管网.

图1 油烟机结构示意图
图2为双吸式多翼离心风机示意图.其主要几何参数分别为叶片数Z=60,叶轮外径D2=230 mm,叶轮内径D1=194 mm,叶轮高度bi=145 mm,叶片进口角β1=76.1°,叶片出口角β2=173.5°,蜗舌半径RV=10 mm,蜗舌间隙dt=13.5 mm,转速n=1 092~1 406 r/min.
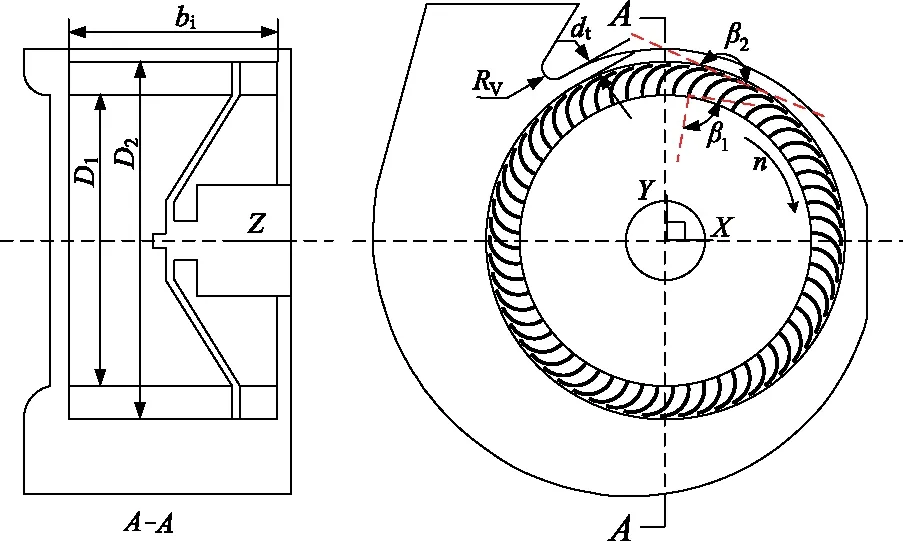
图2 多翼离心风机结构参数的示意图Fig.2 Schematic diagram of structural parameters of multi-blade centrifugal fan
为了方便制造,整个油烟机均采用钣金件.评价油烟机性能好坏的指标有很多,其中最大排烟量是最重要的指标之一.而叶轮作为风机唯一旋转部件,其合适的结构参数会使得风机性能得到一定程度提高[2].为此,文中以风机内部叶轮结构为优化对象,来提高油烟机的最大排烟量.
对叶轮参数化过程中,采用文献[7]叶片参数化方法(见图3)来避免不合理的叶型:用4个控制点P0,P1,P2和P3唯一确定1条二次非均匀B样条曲线作为多翼离心风机的叶片中弧线,而这4个控制点由叶片出口角β2、叶片最大弯曲度f和叶片出口位置Δφ来确定.
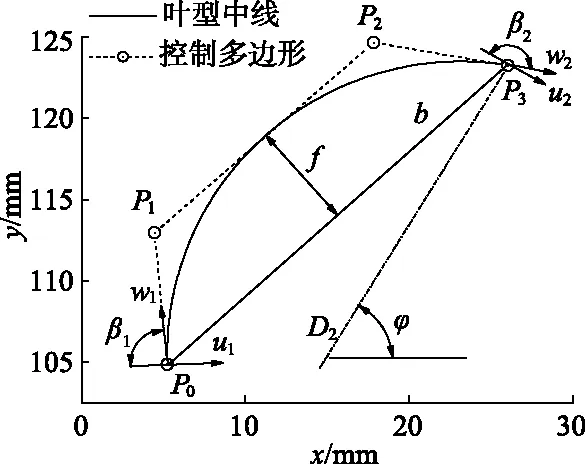
图3 叶型中线几何参数Fig.3 Geometric parameters of middle line of blade profile
整个优化流程如图4所示.

图4 优化流程图
首先确定设计变量的变化范围,利用最优拉丁超立方试验设计方法生成样本并进行数值模拟.以3个设计变量作为输入,油烟机性能参数作为输出,构建回归Kriging模型.按照MSP准则[8]进行加点,当达到回归Kriging模型预测的最优值与CFD计算值之间的差别小于2%时,认为优化过程达到收敛条件.否则将CFD计算的油烟机性能指标与目前代理模型的最优设计参数加入样本空间中,重新构建回归Kriging模型,直到满足收敛条件,完成整个优化流程.
2 CFD方法
为提供稳定入流和出流条件,对进口和出口做适当延长.将计算流域分为4个部分:由进口延长和油烟机腔体等结构组成的油烟机腔体流域、叶轮流域、蜗壳流域、集流器和出口延长组成的出口流域.为建模方便,对油烟机腔体、油烟机腔体中的滤油网、电动机结构等进行简化.叶轮流域进行结构化网格划分,其余流域采用非结构化网格,各个流域通过interface连接.在网格划分过程中,对滤油网、电动机等结构进行网格加密,对蜗壳和叶轮的边界层进行加密处理,计算流域和整体网格如图5所示.

图5 油烟机计算流域和整体网格划分Fig.5 Calculation dornain and overall grid division of range hood
采用Fluent商业软件进行三维流场求解,使用SSTk-w湍流模型求解时均N-S方程,给定全压进口和静压出口边界条件,旋转区域采用MRF多参考系模型,速度和压力耦合采用SIMPLE算法,湍流耗散项、动量方程和湍流动能的离散均采用二阶迎风格式.当进出口流量的波动在2%以内时,认为计算收敛.在最大风量工况(静压ps=0),设置全压进口和静压出口边界条件均为0,对网格进行无关性验证,确定各流域的网格数为叶轮流域网格数272.3万、蜗壳流域网格数157.4万、油烟机腔体流域网格数232.3万和出风流域网格数56.3万,整个流体域的网格数为718.3万.
数值模拟值与试验值相比有较大的误差,如图6所示.其中最高效率点误差在20%以内.造成误差较大的原因可能在于油烟机模型的大量简化以及数值模拟和试验本身误差,如湍流模型和试验设备的误差.但是在最大风量工况下的流量和效率与试验值相比,数值模拟误差在5%以内,而且静压和效率随风量的变化与试验值保持一致.文中目标是优化油烟机的最大排风量,因此,可以用数值模拟的油烟机风量作为参考并进行优化设计.
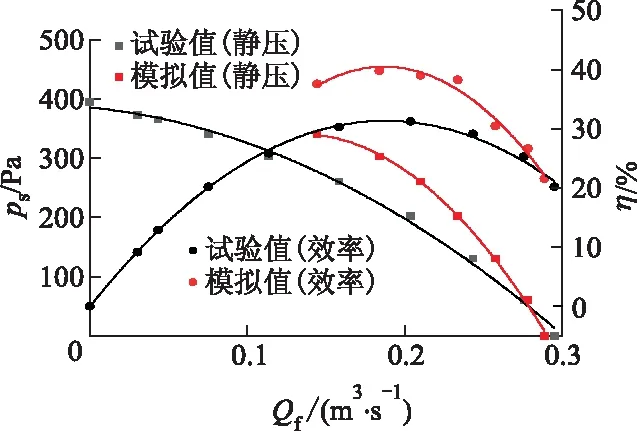
图6 油烟机试验与数值模拟的对比Fig.6 Comparison between experimental and numeri-cal simulation of range hood
3 优 化
在代理模型建立之前,首先应该依据试验设计方法生成样本点,获取关于3个设计变量与最大风量构成的设计空间的信息最大化.根据经验获取3个设计变量为160°≤β2≤177°,5 mm≤f≤8 mm,-2°≤Δφ≤2°.依据最优拉丁超立方试验设计方法[10]生成44组样本,样本分布情况如图7所示.总样本点三维空间分布以及样本点在叶片出口角β2和最大弯曲度f二维投影可以看出,在3个设计参数给定范围内,样本点在空间中的分布比较均匀,有利于构建能够准确预测的回归Kriging模型.
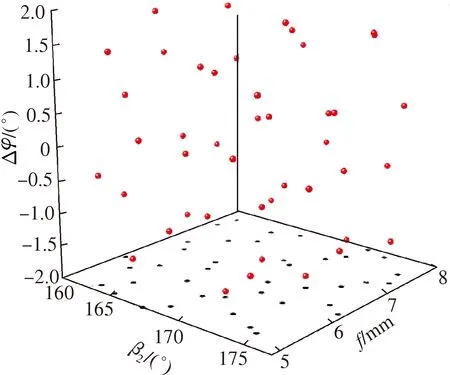
图7 44组样本的分布情况
3.1 回归Kriging模型
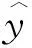
(1)
其中,
(2)
式中:I为单位矩阵;ψ为相关矩阵,由样本点之间的相关函数值组成;1为单位向量;φ为相关矢量,由未知点与已知样本点的相关函数组成[11].
根据式(1)和式(2),以3个设计变量为输入并进行归一化处理(文中将输入参数全部归一化到了0~1内),以消除3个设计参数量级影响.最大流量工况点的风量为输出,构建44组样本的回归Kriging模型,得到回归系数λ的值为-1.801.
44组预测结果如图8所示,从图中可以看出,第25组的相对误差最大,最大为1.38%.在获取回归Kriging模型的基础上,利用遗传算法求其最大值,并将最大值进行CFD验证.

图8 回归Kriging模型的预测结果
利用MSP准则,计算公式为
(3)
文中求风量的最大值,为此需要对风量取负值进行加点,直接将模型获取最优值的CFD验证值和相应的最优设计参数加入样本空间,重新构建新的代理模型.后续加点情况如表1所示.当加点一次的时候,重新得到的回归Kriging模型预测的最优值与CFD验证值相对误差小于2%,认为优化过程达到了收敛.优化后的叶轮使得油烟机最大风量相较于原型机的0.288 1 m3/s提高了11.8%.从数值模拟的优化结果可看出,风机最大风量得到较大提升,但是叶片出口位置Δφ出现在优化的边界上,表明本次优化关于Δφ范围选取不合理,对于提高油烟机的最大风量还可能存在进一步优化空间.

表1 加点情况
将最优方案进行打样试验,与原叶轮对应的油烟机进行对比(见图9),发现优化后油烟机最大流量为0.308 1 m3/s,与数值模拟结果(0.322 0 m3/s)相比,误差为4.5%.由此可见,油烟机优化后的性能与数值模拟得到的优化结果仍存在一定差距,但误差控制在5%以内.优化后的最大风量相较于原型机(0.295 0 m3/s)提高了4.4%,油烟机效率从20.15%提高到21.73%.油烟机在所有工况下的气动性能均得到较大的提升,展现了回归Kriging模型在油烟机性能优化上的优势.

图9 优化前后的试验对比Fig.9 Experimental comparison before and after optimization
3.2 流场分析
基于已获取的优化前后数值模拟结果,选取最大风量工况和最高效率工况,分析叶轮出口截面径向速度随圆周角的变化,如图10所示.将叶轮出口径向速度vr由圆环面沿圆周φ方向展开[12],发现叶轮出口径向速度沿圆周方向呈现非均匀分布,其中蜗舌部分(φ=120°)对应的叶轮流道还出现小范围内回流.相较于最高效率工况,最大流量工况下发生叶轮回流的区域分布更广.叶轮局部回流还会影响蜗壳下游对应的叶轮流道(φ=0~120°)和上游对应的叶轮流道(φ=120°~180°),叶轮出口径向速度相较于主流区域(φ=180°~360°)有较大差距.
图10 叶轮出口截面径向速度云图的对比Fig.10 Comparison of radial velocity cloud diagram of impeller outlet section
从优化后的叶轮出口径向速度云图可以看出,风量增大的主要原因在于主流区域叶轮出口径向速度大幅度提高以及主流区域的分布面积更大.虽然有上述流场的积极变化,但是靠近叶轮前盘的叶轮区域(z=0.15 m,φ=180°~330°),由于风量增大,在主流区的回流增大.主流区径向速度的有利变化,消除了回流带来的消极影响,整体上使得叶轮出口径向速度得到提高,表现为优化后的叶轮使得油烟机风量增大.
对于优化前后蜗壳内部流动影响,截取叶轮中盘截面(z=0.83 m),获取最大流量工况下的静压和流线分布如图11所示.
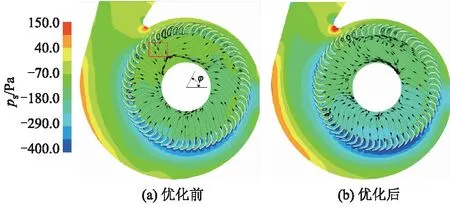
图11 静压分布和流线图
在叶轮进口区域,大部分流体沿着径向进入叶轮,由于蜗舌作用,区域A对应叶道中的流动出现堵塞,甚至回流,加剧了叶轮沿周向上分布的非均匀性.区域A的气体沿着叶轮旋转方向,流入下一个叶道,形成明显的跨叶轮流动现象[12].优化后叶轮,叶片的最大弯曲度更大,叶片出口角减小,使得跨叶轮现象更为明显,气流以更大跨度流入下一个叶道,蜗舌下游区域(φ=0°~90°)叶道中的流动得到一定改善,叶道中旋涡明显减小.在主流区域(φ=180°~360°),叶轮出口静压明显减小,叶道中的旋涡分布范围和规模也大幅度减小,表明优化后叶轮的做功能力明显增强.
根据式(4),对风机的静压恢复系数Cp和全压损失系数Kp进行统计.优化后叶轮使得风机的静压恢复系数从41.65增加到44.29,全压损失系数从15.57减小到9.35.表明优化后的叶轮增强了蜗壳将动压转换成静压的能力,还减少了蜗壳内部流动损失,明显改善叶轮和蜗壳之间的匹配关系.
(4)
式中:下标t和s分别为全压、静压;imp,vol,outlet分别为叶轮、蜗壳和出口;p为压力.
4 结 论
1) 在油烟机性能优化过程中,基于44组样本空间构建的回归Kriging模型能够准确反映叶片出口角β2、叶片最大弯曲度f和叶片出口位置Δφ与最大风量之间的映射关系,最大相对误差为1.38%.根据遗传算法获取最优叶轮参数,叶片出口位置Δφ出现在边界范围内,表明最大风量还有进一步提高的空间.
2) 利用最小化代理模型预测准则的加点方法,经过一次加点就满足了收敛条件.对最优叶轮设计参数进行打样试验,相较于原型机,油烟机最大风量提高了4.4%,最大风量工况下效率提高了1.58%,油烟机在全工况下的风机性能均得到较大提升.结合内部流场分析,风量提高的主要原因在于主流区域叶轮出口径向速度的大幅度提高以及主流区域的分布面积更大,优化后叶轮明显改善油烟机叶轮和蜗壳之间的匹配关系.

