混流泵启动过程瞬态特性的数值计算

赵文斌，李伟，王行元，马凌凌，季磊磊

(1. 江苏大学能源与动力工程学院，江苏 镇江 212013； 2. 江苏大学国家水泵及系统工程技术研究中心，江苏 镇江 212013; 3. 中船重工集团有限公司第七〇五研究所昆明分部，云南 昆明 650101)

混流泵广泛应用于南水北调工程、水下导弹和鱼雷发射系统、舰船喷水推进系统、海水脱盐系统以及火力发电和核电站的循环水系统等，是国民经济重要的动力装备[1-3].混流泵启动作为一类特殊的瞬态过程，可为特殊的应用场合提供瞬时流体动力.但混流泵启动时，流量、扬程和转速以及泵内部流动结构在短时间内发生快速变化，由此引发叶轮流道内局部负压、瞬时高压和空化等现象[4-5]，对泵装置产生较大负面效应，危害机组运行安全.

国内外学者对泵启动过程的瞬态特性进行了大量的理论、试验及数值模拟研究.TSUKAMOTO等[6-7]通过对离心泵进行快速启动与停机试验，发现相比于准稳态，瞬态启动过程中的压力脉冲与绕叶片环量延迟的共同作用造成了两者之间性能的差距.LEFEBVRE等[8]在专用试验台上对比分析了3种不同启动时间下的启停瞬态特性，研究表明，叶轮加速是造成准稳态预测不准确的最主要原因.DAZIN等[9]基于角动量和能量方程推导得出瞬态启动过程中的水力扭矩和理论扬程公式.陈宗贺等[10]对启动过程的空化特性进行了高速摄影研究，表明启动初期无明显空化现象，随着转速增大，在叶顶间隙处首先出现空化.

目前，关于流体机械启动过程的数值模拟方法主要有2种：一种是以试验测得的转速和流量作为边界条件进行的数值计算[11-12]，另一种是给定启动转速的闭合回路全三维流场的数值计算[13-15].LI等[16]采用区域动态滑移网格法(DSR)和层流模型对离心泵启动过程进行数值模拟， 验证了 DSR 方法在离心泵瞬态流动模拟中的有效性. 陈宗贺[17]对混流泵进行了不同启动时间与流量工况下的数值计算，发现湍动能较大的区域集中在叶顶区域，且不稳定流动显著.薛宏林等[18]基于特征线法对立式混流泵站停泵、关阀两阶段过渡过程的瞬态特性进行研究，分析了不同快关角度与慢关时间组合情况下倒泄流量、倒转转速和水锤压力的变化规律.王勇等[19]对超低比转数离心泵的关阀状态进行启动分析，研究表明管阀启动瞬态流场存在明显滞后性，蜗壳内部瞬态流动比稳态时更加紊乱.李伟等[20]基于涡动力学方法对进口管、叶轮及导叶内部流场进行了分析，发现进口管截面涡核在启动初期较为分散，而后聚集，稳定后反向涡消失.

虽然国内外学者对泵启动过程的瞬态特性进行了大量研究，但在现阶段，对于混流泵的启动过程，尤其在不同启动条件下的泵内流动研究还不够深入.因此，文中在建立混流泵启动过程瞬态流场数值求解的计算模型和方法的基础上，对泵启动过程静压场、涡量场及流线分布随时间的演化过程进行解析，并对比分析不同启动条件下瞬时扬程、流量的变化规律.

1 数值计算

1.1 计算模型

文中所研究的混流泵设计性能参数分别为流量Qd=380 m3/h，扬程H=6 m，转速n=1 450 r/min，比转数ns=480.混流泵叶轮叶片数Zi=4，导叶叶片数Zg=7.采用Pro/E软件对该混流泵进行三维建模，包括进口段、叶轮、导叶、蜗室和出口段，如图1所示.

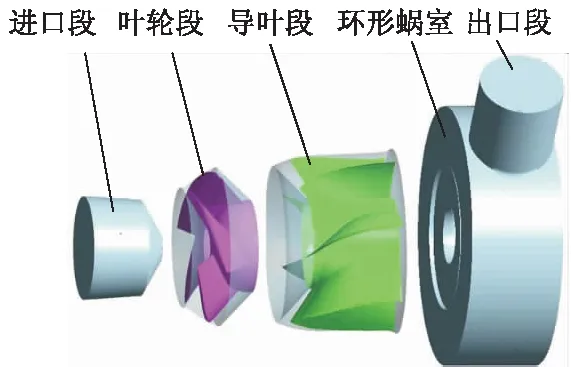
图1 混流泵模型

1.2 网格划分及无关性验证

采用ICEM软件对计算模型进行六面体网格划分，其中叶轮采用J/O型拓扑结构，导叶采用H/O型拓扑结构，进口段采用Y-block型拓扑结构.全流道计算网格如图2所示.

图2 全流道计算区域网格Fig.2 Computational domain mesh of whole flow passage

在设计工况下对混流泵模型所划分的网格数进行无关性验证，基于相同的网格拓扑结构，在保证网格质量的前提条件下，通过改变节点数与网格尺寸大小控制整体的网格数量.图3为5种不同网格数时泵扬程的对比，可以看出，当计算模型网格数N达到110.01万时，网格数对扬程影响较小，误差在±5%以内，符合网格无关性检验要求.

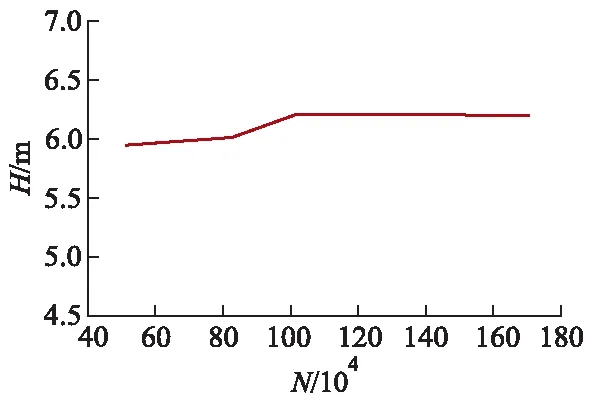
图3 不同网格数下泵扬程对比Fig.3 Comparison of pump head with different mesh elements

1.3 湍流模型与边界条件设置

由于Standardk-ε湍流模型能够较为准确地预测泵启动过程的外特性并反映其内部流动[12]，故采用该模型进行研究.数值计算中，假设整个启动过程泵内流动为湍流，以时均化纳维-斯托克斯方程作为基本控制方程，选用Standardk-ε双方程湍流模型，采用基于微元中心有限体积法空间离散方式实现压力速度耦合求解.连续方程与动量方程离散格式分别为

(1)

(2)

为保证动静计算域数据传输的准确性，采用多重坐标系算法，选择Transient Rotor Stator连接叶轮与导叶、叶轮与进口交界面.基于试验转速与流量作为边界条件，调用CEL表达式控制叶轮的加速过程.进出口边界条件设置为“Opening”.转轮室壁面设置为“The Counter Wall”.静止域壁面采用“No Slip Wall”.不同加速条件下(启动时间分别为0.8，1.0和2.0 s)计算取相同采样频率，计算步长分别为0.000 8，0.001 0和0.002 0 s，残差收敛精度设为10-4.

2 数值计算方法的试验验证

图4为准稳态及瞬态数值计算得到扬程曲线与试验扬程曲线的对比.

图4 数值预测结果与试验结果对比Fig.4 Comparison between calculation and test results

由图4可以看出：准稳态扬程随着转速的增大呈直线增大的变化趋势，在启动过程中基本上大于瞬态数值计算扬程与试验扬程，这主要是因为准稳态扬程完全满足相似定律，并没有考虑角加速度与流体惯性影响；瞬态数值计算扬程与试验扬程则保持了较好的一致性，均随着转速增大而增大，并且在转速达到最大时扬程也达到最大；由于惯性的影响，流量出现明显的滞后现象，此时的瞬时流量小于稳定后的流量；在启动结束时刻，启动扬程存在明显的冲击现象，这主要是由于受到2个方面因素影响，一是角加速度产生的附加扬程，二是启动结束时仍处于小流量工况运行；启动结束后，三者的扬程值均随时间而缓慢降低，并在约3 s时刻趋于稳定；对比稳定扬程，3种瞬态冲击扬程均在1 m左右，因此，可以判定小流量工况对冲击扬程的影响占据主导；整体上，瞬态数值计算结果更为可靠.

以量纲一化扬程系数随时间的变化来描述混流泵的启动过程，其表达式为

(3)

式中：H为瞬态扬程；u2为出口边圆周速度.

试验、瞬态计算与准稳态计算三者的量纲一化扬程系数随时间变化如图5所示，通过对比可以看出，准稳态数值计算量纲一化扬程系数变化比较平稳，瞬态数值计算与试验的量纲一化扬程系数比较接近，在启动初期其值均较大，并随启动时间快速下降至点A与准稳态重合，点A以后瞬态计算量纲一化扬程系数与试验量纲一化扬程系数开始小于准稳态值，并出现波动现象.由于瞬态数值计算与试验扬程不是在同一时刻达到最大值，瞬态数值计算扬程与试验扬程先后与准稳态计算扬程在点B与点C重合，此后三者的变化一致，说明混流泵进入稳定运行状态.

图5 启动过程试验与数值计算量纲一化扬程系数曲线Fig.5 Comparison of head coefficient between experiment and simulation

对比分析准稳态数值计算、瞬态数值计算与试验量纲一化扬程系数三者的变化可知，从启动开始至点A，由于启动角加速度引起的压力突增，瞬态量纲一化扬程系数远大于准稳态值.从点A至点B，由于这段时间内泵内流体惯性影响较大，惯性消耗使得扬程小于准稳态值.点B以后，角加速度与流体惯性影响甚微.总体上，实际启动扬程系数存在明显偏离准稳态的现象，这也体现了启动过程中的显著瞬态特性.

3 瞬态数值计算结果及分析

3.1 启动过程内流场分布

图6为混流泵启动过程中不同时刻的压力分布云图，可以看出：在t=0.005 s时刻，叶轮仅仅转过微小角度，此时由于叶片与流体的剪切作用与流体惯性的共同作用，工作面的进口附近的压力梯度比较明显，受角加速度效应与流体惯性的综合影响，工作面靠近出口侧出现大片的高压区，由于流体受惯性力作用保持原有状态继而存在偏离叶片背面的趋势，使得叶片背面侧压力较低；在t= 0.050 s时刻，叶片对流体做功明显，叶片与导叶内的压力均有明显增加；在t= 0.150 s时刻，叶片压力面高压区集中在轮缘与轮毂两侧；随着半径和转速的增大，叶片对单位流体的做功能力增强，在t=0.850 s时刻，高压区仅存在轮缘附近；在t=1.350 s时刻，内部流动逐渐稳定并更加均匀.

图6 启动过程中泵内压力云图

图7为启动过程叶轮表面静压及流线分布，可以看出：在t=0.005 s时刻，转速较低，虽然叶片进口处流体做剪切运动，但由于流体在惯性力影响下具有初始静止流态特性，因此叶片压力面进口边压力梯度大，进口存在明显的回流，同时，由于泵做功能力差，叶轮内部旋涡强度弱、范围小，因此旋涡区域仅出现在叶片出口边与轮缘间隙处的较小范围内；在t=0.050 s时刻，在叶片吸力面与轮毂附近存在旋涡，工作面的回流范围扩大并偏向轮缘区域，随着转速增大，叶片工作面与背面间的压差增大，轮缘间隙泄漏流与主流汇合，二者相互作用并在叶片进口边附近的较小区域范围内产生旋涡；在t=0.500 s时刻，在靠近叶片进口边的轮缘间隙处和叶片出口边尾缘处均有旋涡产生，压力面流体总体上从轮毂处向轮缘处流动，此时泵内部流场较为紊乱；在t=0.850 s时刻，仅在进口边的轮缘间隙处有比较显著的涡核显现，轮缘泄漏流是造成这一现象的主要原因，此时流线分布表明叶轮内无明显旋涡堵塞流道，由于叶轮外侧的离心力作用较大，再加上流体惯性力的影响，流线仍然具有偏向轮缘的发展趋势；启动结束时刻，结合外特性曲线可以看出，此时泵依然处于非稳定流动阶段，流量继续缓慢增大而扬程则逐渐减小，由于惯性力影响，变化趋势与稳态非定常内流场存在一定差别.

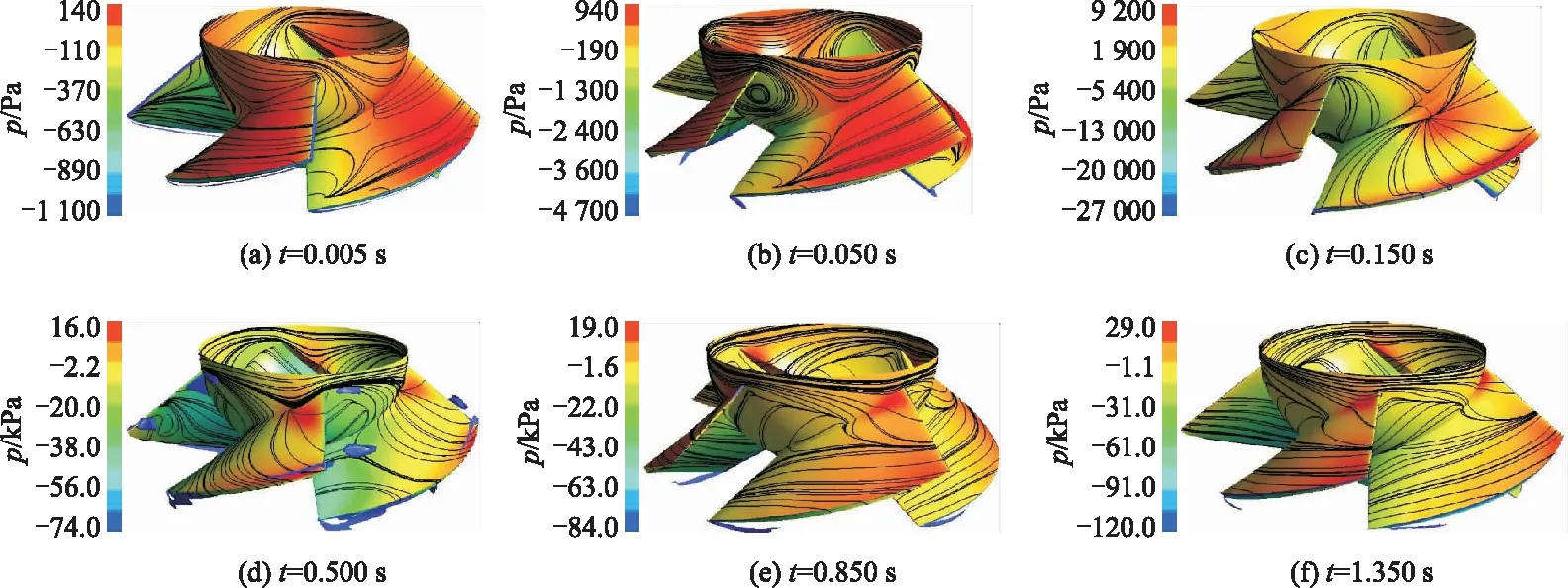
图7 启动过程中叶轮表面静压及流线分布

图8为启动过程中轴面流速随时间的变化情况，可以看出：在t=0.005 s时刻，由于转速较低，叶片做功不足，大部分回流占据了轮毂至半倍叶高处区域，轮毂侧尤为显著，轮缘区域附近存在由于间隙泄漏流引起的回流，同时，由轮毂向轮缘的速度分层效应明显，这是由于初期的流体惯性造成；在t=0.050 s时刻，轮缘处回流存在向进口方向聚集的趋势，而轮毂处的高速回流区向轮毂中部聚集；在t=0.150 s时刻，轴面流速的分布不规则化愈发明显，说明内部流动湍流化程度逐步加剧，轮毂中部的高速回流聚集现象非常显著；在t=0.500 s时刻，最大速度明显增大，泵内部流动比较紊乱，轮缘处的圆周速度与轮缘泄漏流的综合作用导致轮缘进口存在明显回流区，叶轮出口和导叶进口之间也存在回流；随着转速增大，轴面流速分布在t=0.850 s时刻以后趋于一致，叶轮做功能力的增大使得轮缘进口处的轴面流速不断增大，仅在轮毂出口处存在回流.

图8 启动过程中轴面流速分布

3.2 启动加速度对瞬态特性的影响

为探究启动加速度对瞬态特性的影响，选取3种启动时间(0.80，1.00和2.00 s，转速在对应的启动时间内从0均匀增大至1 450 r/min)进行瞬态数值模拟.为了避免转速与流量的试验误差，选择在阀门全开时对混流泵进行启动过程数值模拟.

3.2.1 瞬态外特性对比

3种启动加速度下泵扬程的变化趋势如图9所示.由于模拟的是阀门全开状态下的启动过程，因此稳定流量较大，图中的泵扬程也较低.可以看出，3种启动加速度下，扬程与转速均在启动结束时同时达到最大值.

图9 3种启动加速度下扬程的变化趋势Fig.9 Comparison of head evolution under three starting accelerations

3.2.2 瞬态内流场

图10为3种启动加速度下，瞬时转速达到750 r/min时流场内压力与流线分布，可以看出：叶片工作面的高压区域随着加速度的减小略有减小，不同启动加速度下，导叶内均存在明显旋涡，并且随着加速度减小，导叶轮毂处的旋涡逐渐由导叶进口向出口转移；在0.80 s启动加速度下，导叶凹面进口流线分布较为均匀但是在中部靠近轮毂处存在回流；随着启动加速度的减小，凹面进口流线逐渐向轮缘处聚集.这表明启动加速度对内部流场存在较大影响，加速度越大，泵内流场分布越紊乱.内部流场的瞬态变化与趋势表现为瞬时扬程的水力冲击和流量的滞后效应.

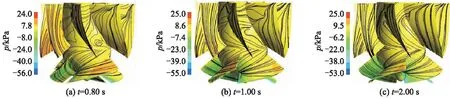
图10 3种启动加速度下静压及流线分布

4 结 论

1) 基于相似理论建立的准稳态方法不适用于混流泵启动过程瞬态水力特性模拟，整体上，瞬态数值计算方法较为可靠.

2) 在混流泵启动过程中，叶片进口边表面压力梯度由于惯性作用比较明显，工作面高压区偏向出口处且随时间的推移逐渐收缩至叶片出口轮缘处.启动初期叶轮进口存在明显回流，在惯性力和离心力的共同作用下，流线一直具有向外缘偏转的趋势.启动过程中由于泄漏流的影响，叶顶间隙附近存在明显旋涡.

3) 在混流泵启动过程中，随着启动加速度的减小，由角加速度和流动惯性等共同引起的冲击扬程也随之减小甚至消失，这表明流量滞后性随启动加速度的增大而减小.启动加速度对内部瞬态流场的影响较大，加速度越大，混流泵启动过程瞬态内流场越紊乱.