基于不同曳力模型的鼓泡流化床CFD-DEM数值模拟与试验研究
白玲,韩晨,徐云峰,周岭*,张铃杰,施卫东,3
(1. 江苏大学国家水泵及系统工程技术研究中心,江苏 镇江 212013; 2. 昌吉学院物理系,新疆 昌吉 831100; 3. 南通大学机械学院,江苏 南通 226000)
鼓泡流化床广泛应用于煤燃料脱硫脱硝、颗粒燃烧以及机械零部件的涂装等国民生产领域[1].多年来,国内外相关学者开展了大量的试验测量对流化床最低流化速度、床层高度、颗粒局部聚集等内部流动机理进行研究.但是由于气固两相流动的复杂性以及不确定性,试验研究难以获得微观尺度的颗粒运动信息[2].
随着计算机技术以及并行计算的发展,数值模拟方法成为研究流化床内部流动特性的主要手段.目前,对气固两相流动的数值计算主要有2种方法:第一种是欧拉-欧拉法,该方法将颗粒相看作拟连续相,基于传统流体力学理论,分别解两相的连续性方程;第二种方法是欧拉-拉格朗日法[3], DEM属于欧拉-拉格朗日法中的一种,该模型通过计算牛顿运输方程以描述颗粒的移动和旋转运动,同时能够兼顾颗粒-颗粒、颗粒-壁面之间的碰撞,它突破了传统的DPM方法仅能计算固相体积分数小于10%的稀相流动的瓶颈,因而该模型在稠密两相流中得到广泛应用.颗粒动力学理论认为曳力是气固两相流系统中最主要的力,当流体施加在颗粒上的曳力平衡颗粒自身重力时,颗粒悬浮[4].不同学者根据大量的试验结果总结出多种不同的曳力模型,目前在DEM模型架构下,应用于流化床中气固两相流的曳力模型主要有Ergun,Wen & Yu,Syamal- O′Brien,Gidaspow,Di Felice,Huilin & Gidaspow这6种[5-8].由于试验环境以及流化床内部流动的复杂性,在计算颗粒两相流场时对曳力模型的选择一直是困扰众多学者的难题.郑晓野等[9]针对低颗粒浓度范围内曳力下降的问题通过光滑函数改进了曳力模型,并将模拟结果和Gidaspow,Syamal-O′Brien模型对比,发现改进的曳力模型能更好地描述两相流动; VISURI等[10]依据欧拉双流体模型对二维鼓泡流化床进行数值仿真,指出要依据系统性能选择曳力模型以提高数值模拟精度.
由于缺乏对机理的理解,到目前为止,尚未建立令人满意的通用方法来解释这些机理并预测两相流流动过程.文中基于DEM数值模拟以及准二维流化床高速摄影试验,分别对比床层高度、空泡直径,颗粒速度分布以及压力波动,研究6种常用的曳力模型数值计算结果,以期为大尺度流化床数值计算和优化设计提供理论参考.
1 数学模型
DEM模型属于软球模型,该模型在考虑颗粒相互干涉的同时,考虑颗粒相、连续相在计算微元中的体积分数.假设εg为气相体积分数,流体相的质量、动量守恒方程分别为

(1)
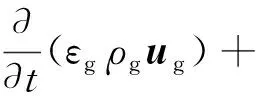
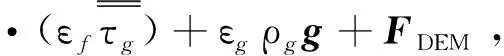
(2)

对于颗粒相的移动和转动的描述主要通过解经典牛顿力学方程,即
(3)
(4)
文中采用弹性-阻尼器模型对碰撞过程中颗粒所受的短程作用力进行计算,该模型包含胡克弹性模型以及牛顿阻尼器模型.
2 试验和数值模拟方法
为了直观地观察流化床内部的气泡及颗粒流动特性,因而考虑将三维流化床简化为准二维流化床,减少数值计算时间.在江苏大学流体中心实验室搭建了一个流化床高速摄影试验台,如图1所示.
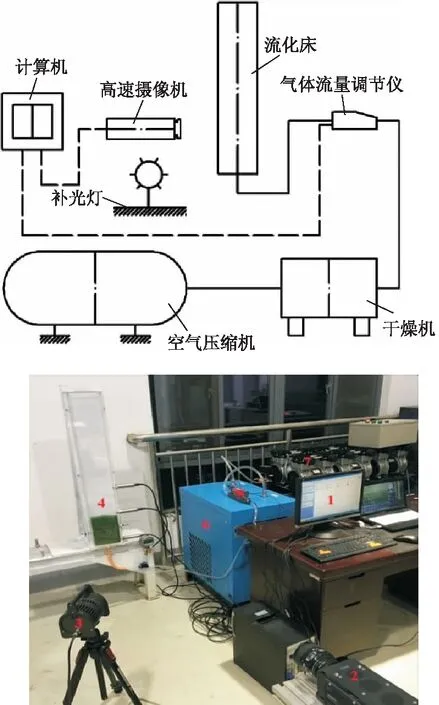
图1 流化床高速摄影试验Fig.1 Test rig for fluidized bed high speed photogra-phy experiment
空气由空气压缩机加压,经冷冻式干燥机干燥后通过高精度质量流量控制器进行流量调节,再进入流化床中.在长、宽、高分别为15,2,100 cm的准三维流化床内布置36 500个平均直径为2.5 mm的玻璃球,初始堆积高度为17 cm,在流化床侧边2,22,40 cm高处分别布置3个压力监测点.压力传感器的型号是CY200,采样频率为1 kHz,流化床底部中心开一个孔,通入初始速度为350 L/min的空气.质量流量为0.007 kg/s,为了防止颗粒被吹出,在流化床顶部布置了一张滤网,由于流化床较高,可以忽略滤网对整个系统压力降的影响,通过正面放置的高速摄影机对流化床内鼓泡的运动以及颗粒的流动进行拍摄.高速摄影的拍摄频率是1 000 s-1.
为了使得流体相的网格尺寸大于颗粒相的,在划分流化床网格模型的时候,通过网格无关性分析最终确定网格尺寸为颗粒直径的2.5倍,网格总数为22 880个的六面体网格模型,同时在模拟过程中流化床入口为中间位置采用了和9个圆形面积相等的矩形,矩形的长和宽分别为5.6 mm和5.0 mm,模拟过程中边界条件设置为质量流量进口和压力出口,为了描述湍流对流动的影响,采用标准k-ε湍流模型描述湍流对流动的影响, 进口处的湍流强度设定为5%.
3 讨 论
3.1 鼓泡形态
图2为在0~450 ms时间段内6种曳力模型的数值模拟结果与试验结果的对比.在t=0 ms时刻,试验中流化床颗粒床层初始堆积高度为17 cm,根据鼓泡的形态,在0 图2 进口速度350 L/min下0~450 ms时间段内数值模拟结果(红色)和试验结果(黑色)对比Fig.2 Comparison of experimental(black) and numerical results (red ) from 0 to 450 ms with inlet speed of 350 L/min 图3为流化床床层高度的不同曳力模型与试验对比结果.从图中可以看出流化床床层高度的变化趋势是先上升后下降,这主要是因为在0~300 ms阶段,流化床中多余的气体在流化床内部形成鼓泡,由于持续不断的通气,使得鼓泡不断向上运动,推动了鼓泡顶部的颗粒层也向上运动,在300 ms时刻鼓泡发生了破裂,此时气体逸出了颗粒床层,夹带了部分颗粒弹射出流化床顶部自由表面,此时床层高度继续向上运动,在350 ms时刻床层高度达到最大值,此时流化床颗粒床层内部的压力与大气压一致,大部分的气体都通过流化床顶部较大的颗粒间隙逸出流化床,流化床的高度开始下降,根据不同曳力模型的数值计算结果,Gidaspow曳力模型与试验结果吻合度最高,Huilin & Gidaspow,Syamal-O′Brien和Ergun曳力模型都较高地预测了床层高度的变化趋势,Di Felice曳力模型低估了床层高度的变化,而Wen & Yu曳力模型在0~350 ms阶段高估了床层高度的变化,但是在鼓泡破裂后床层高度的回落过程中又低估了试验值,因此综合整个变化趋势,Gidaspow曳力模型的表现最好,而在鼓泡形态方面表现突出的Huilin & Gidaspow曳力模型则高估了试验值Hbed的变化. 图3 床层高度的不同曳力模型数值模拟结果和试验对比Fig.3 Comparison between experiment and simulation results of different drag models for bed height 床层高度和鼓泡面积是衡量鼓泡流化床内部流动性能的重要标尺.为了量化鼓泡的尺度,采用等效气泡直径公式计算,即 (5) 式中:Abub为鼓泡在高速摄影平面的投影面积. 图4为流化床床层鼓泡面积的不同曳力模型与试验对比结果,可以看到试验中鼓泡面积基本上在300 ms时刻达到最大值,Gidaspow模型在200 ms时刻之前与试验值比较吻合且小于试验值,但在200 ms时刻之后预测值高于模拟值,但总的趋势是一致的,同时可以看出基本上所有的曳力模型预测值在200 ms时刻之后都高于试验值,其中Wen & Yu曳力模型与Di Felice曳力模型与试验结果比较接近,Huilin & Gidaspow,Syamal-O′Brien和Ergun曳力模型都高估了鼓泡面积直径的变化. 图4 鼓泡直径的不同曳力模型数值模拟结果和试验对比Fig.4 Comparison of bubble diameter between expe-riment and simulation results of different drag models 从图2中可以看到试验中鼓泡发展到后期出现了第二级小气泡,因此为了分析曳力模型对于第二级小气泡的预测情况,直接采用小气泡的面积来进行对比,主要是因为出现的第二级小气泡在横向方向尺度较大而在纵向方向尺度较小,其纵横比较小,如果采用等效直径的方法不能够体现纵横比小这一特性.从图5可以看出Huilin & Gidaspow与Gidaspow曳力模型与试验过程中第二级小气泡的面积变化趋势一致,其他曳力模型没能够符合小气泡面积持续增大这一趋势,特别是Di Felice曳力模型没有预测出第二级小气泡的现象,综合发现Huilin & Gidaspow与Gidaspow曳力模型表现较好. 图5 第二级小气泡面积的不同曳力模型数值模拟结果和试验对比Fig.5 Comparison of second-stage small bubble area between experiment and simulation results of different drag models 图6为6种曳力模型的轴向时均速度va对比,通过对比可以看出,轴向时均速度的分布为中心速度高,两侧速度低,而且时均速度大小的变化趋势在横向方向是从边壁区到中心区先增加然后减小然后再增加,而且边壁区的速度方向是向Z轴负向即颗粒的运动方向是向下运动的,这说明了颗粒的返混现象,由于鼓泡的运动以轴向运动为主,因此中心轴向速度较大.根据数值模拟结果Ergun模型的中心速度比其他曳力模型高许多,Gidaspow的中心速度比其他曳力模型稍低,其他4种模型的速度变化分布基本一致. 图6 z=10 cm处z向速度的6种曳力模型的数值模拟结果对比Fig.6 Comparison of simulation results of the six drag models with z-direction velocity at z=10 cm 文中在自行搭建的流化床高速摄影试验台的基础上,基于CFD-DEM方法,针对目前流化床中稠密气固两相流中Ergun,Wen & Yu,Syamal- O′Brien,Gidaspow,Di Felice以及Huilin & Gidaspow共6种曳力模型进行了数值模拟,并将模拟结果与试验结果进行了对比. 总体上,在鼓泡形态的预测方面Huilin & Gidaspow与Gidaspow模型能够对鼓泡的形态以及鼓泡破碎后出现的二级小气泡进行比较准测的预测,但是在流态化特性的对比中,Gidaspow模型能够在床层高度以及鼓泡的当量直径方面具有明显的优势,而Huilin & Gidaspow,Syamal-O′Brien模型以及Di Felice模型较高的估计了床层高度变化,因此,在基于CFD-DEM的流化床数值模拟中,Gidaspow模型能够对稠密气固两相流动进行较为准确的预测,在空泡形态和压力波动与试验吻合较好,为工业中流化床的设计与优化提供一定的理论参考.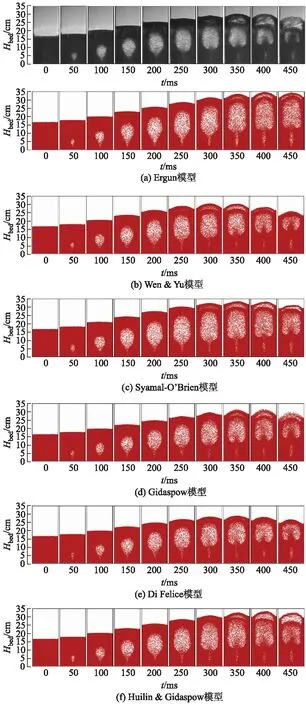
3.2 床层高度

3.3 鼓泡特性


3.4 颗粒速度分布

4 结 论

