风荷载对高耸电塔拆除爆破影响研究及实践

张西良，崔正荣，仪海豹，刘为洲，杨海涛

(1.中钢集团马鞍山矿山研究总院股份有限公司，安徽 马鞍山 243000；2. 马鞍山矿山研究院爆破工程有限责任公司，安徽 马鞍山 243000；3. 金属矿山安全与健康国家重点实验室，安徽 马鞍山 243000)

拆除爆破是采用炸药爆炸能量拆除建(构)筑物的重要技术手段，在社会城镇化建设过程中发挥了不可磨灭的作用。经过多年的理论研究及拆除实践，取得大量研究成果和总结经验。我国的冯叔瑜、汪旭光、于亚伦和谢先启等[1-5]专家教授组织编写了多部控制爆破著作，为拆除爆破理论与技术的发展奠定了坚实基础；贾永胜、钟明寿、张广荣等[6-8]采用数值模拟手段研究了拆除爆破倒塌规律，并进行了现场实践验证。

本文以长江沿岸某废弃高耸电塔为例，推导了电塔倒塌方向偏转角理论公式，并研究了风向、风速和风振效应对电塔拆除爆破偏转角的影响规律；最后通过组织设计施工，成功实现了电塔的定向拆除爆破，较好地验证了理论分析的可靠性，对类似拆除爆破具有一定指导借鉴作用。

1 工程概况

“皖江第一跨”即 220 kV皖中大跨越，是安徽第1座220 kV大跨越长江输电通道，担负着安徽北部与华东电网联络重任。皖中大跨越采用耐-直-直-耐的跨越方式，长江两岸各有一座分裂式混凝土塔，分别称为南塔和北塔，两塔跨越距离1 411 m。该线路于1960年建成投运，2014年退役。

北塔位于长江西岸和县西梁山镇聂庄村长江大堤外。北塔周边地势平坦，距西北侧036县道(长江大堤)89 m，距养殖大棚167 m，距北侧小朱庄177 m，距东侧长江203 m(见图1)，周边环境十分复杂。

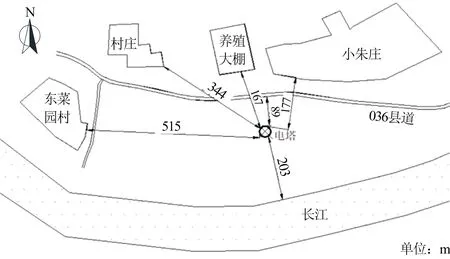
图1 电塔周围环境Fig.1 Electric tower surroundings

电塔为钢筋混凝土结构，塔高117 m(其中塔体结构高105 m，塔顶Y型横担高12 m)，底部直径13 m，顶部直径4.0 m，塔筒壁厚0.2～0.4 m(底部壁厚大、上部壁厚小)。塔筒内设有钢梯，供检修人员使用。电塔退役后，塔身混凝土风化开裂严重，甚至成块脱落，影响塔筒结构的安全。为消除塔体安全隐患，计划予以爆破拆除。

该电塔拆除爆破的主要技术难点有：塔顶的横担未拆除，影响塔体偏转角；塔体高度大，风荷载对偏转角影响大；周边需要保护对象多、环境复杂，爆破飞石和振动等危害控制难度大。

2 电塔倒塌方向偏转角理论推导

假定爆破切口形成瞬间，切口底部余留支撑体截面上的应力按线弹性分布。根据材料力学知识，建立余留支撑体截面特性参数计算简图(见图2)，图中阴影部分为余留支撑体截面，ox方向为设计预倾倒方向；c为切口形成后余留支撑截面的形心；R1为切口底部筒体内半径；R2为外半径。

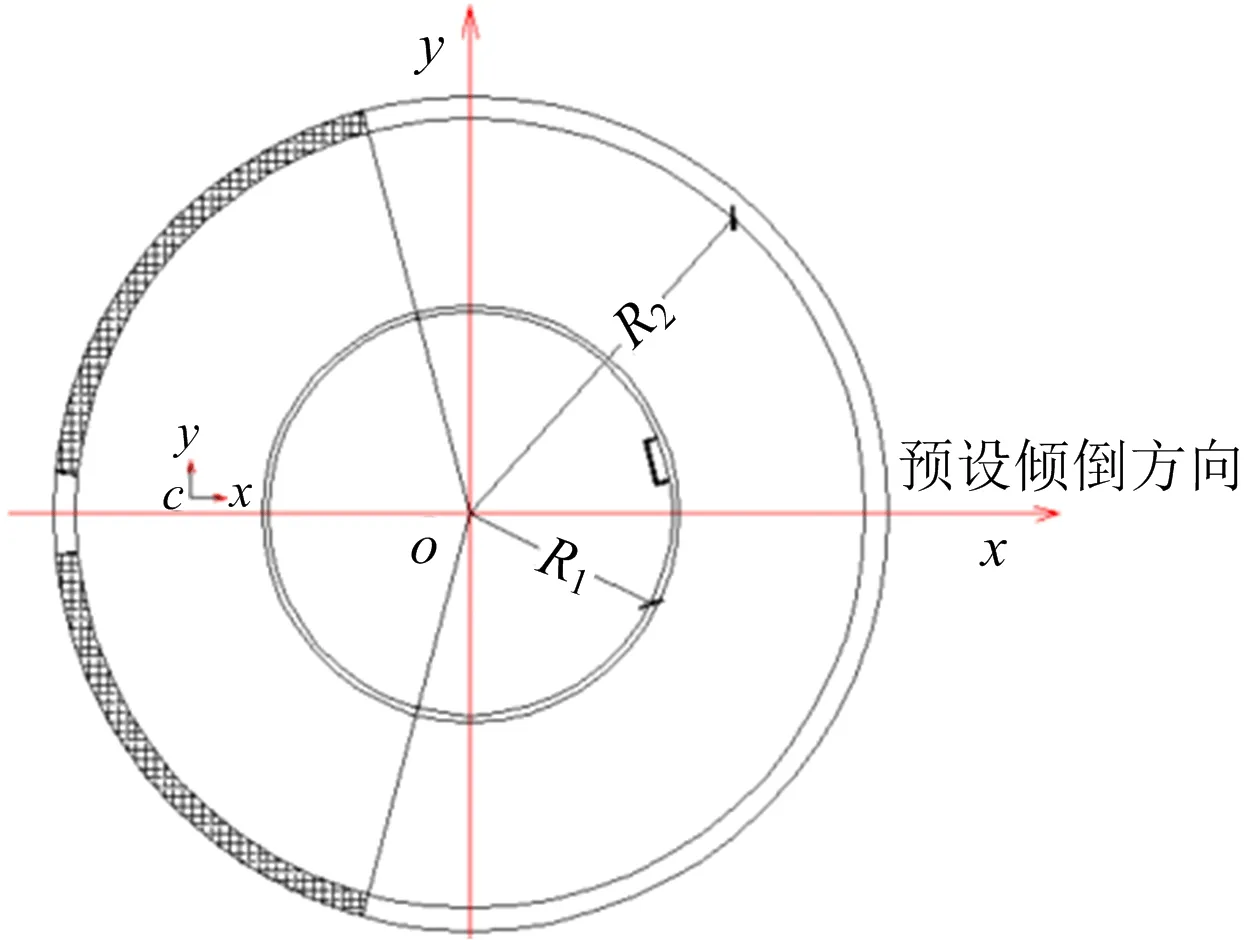
图2 爆破切口截面参数Fig.2 Section parameters of blasting cut

现将坐标原点移至c点，以cxy为参考坐标系，分析截面上的应力。余留支撑体截面上由自重产生的均布压应力为

(1)

式中：G为切口底部截面以上结构自重；A0为考虑配筋后的余留支撑体截面的折算面积。

在绕cy轴、cx轴的弯矩Mcy、Mcx共同作用下，截面上任一点的应力σ2为

(2)

此处Icxy=0，上式可简化为

(3)

式中：Icx、Icy、Icxy分别为切口底部支撑体截面关于cx、cy轴的惯性矩和惯性积。

切口底部截面上任一点的合应力为σ=σ1+σ2。

假定点(x0,y0)为支撑体截面中性轴上任一点的坐标，则中性轴上各点的正应力均为0，将(x0,y0)代入应力表达式中，则有

(4)

中性轴方程为

(5)

中性轴斜率方程为

(6)

由于倒塌中心线与中性轴直线相互垂直，假设电塔倾倒偏转角为φ，即倒塌方向与cx轴正向夹角(逆时针为正，顺时针为负)，则有

(7)

(8)

3 风荷载对电塔倒塌方向影响分析

3.1 顺风向风载下倒塌方向偏转角计算

根据《建筑结构荷载规范》[9]，垂直作用于电塔表面单位面积的风荷载标准值表示为

Wk=βzμzμsw0

(9)

式中：w0为基本风压，对于高耸结构物电塔采用1.1的增大系数；βz为距塔体底部高度z处的风振系数；μs为风荷载体型系数，取0.56；μz为风压高度变化系数。

考虑到μz和βz在结构高度方向的分布是顶部最大，为简化计算，这里取沿最大风压高度变化系数μzmax和结构顶部的风振系数βzmax计算风荷载标准值，即

Wk=1.1βzmaxμzmaxμsw0

现场风荷载作用对电塔产生倾倒旋转弯矩(侧向弯矩)。将风荷载等效为均布荷载作用于电塔表面，计算爆破切口底部风载倾覆弯矩时，将塔体的受荷面积等效成梯形截面(见图3)。

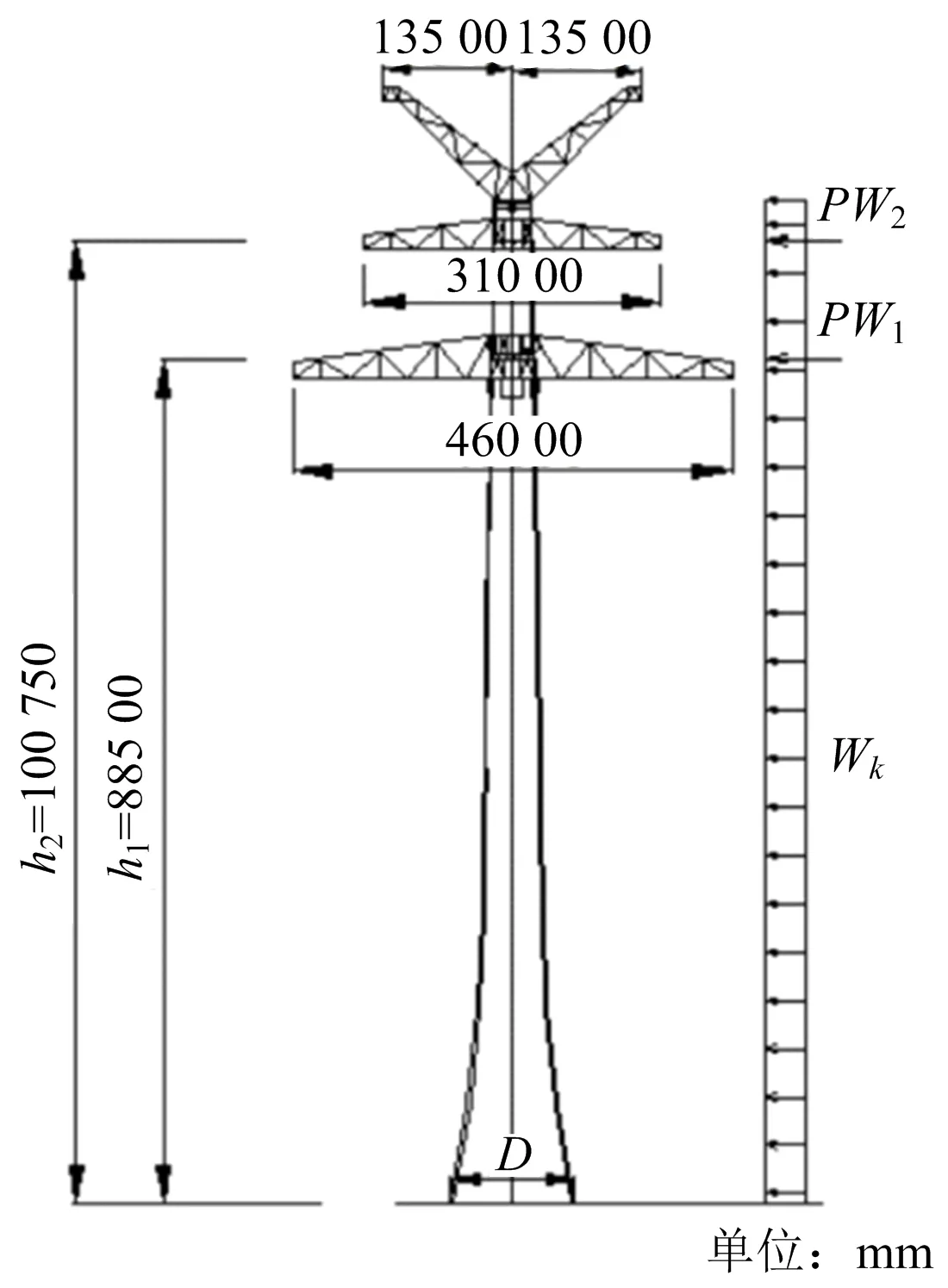
图3 风荷载计算Fig.3 Wind load calculation

混凝土塔体风载合力可表示为

(10)

式中：H为塔体结构总高度，105 m；d为塔体结构顶部直径，4 m；D为塔体结构底部直径，13 m。

合力作用位置距离塔体底部高度为

(11)

假定切口底部距地面高度h0=0.5 m，均布风荷载在切口底面的弯矩Mw为

Mw=Fw(Hw-h0)+PW1(h1-h0)+PW2(h2-h0)

(12)

式中：PW1为下横担正面风荷载，kN；PW2为顶部两横担正面风荷载，kN；h1为下横担的高度，88.5 m；h2为顶部两横担的高度，100.75 m。

下部横担和顶部羊角横担处桁架和节点挡风的净投影面积分别为23.47 m2和18.66 m2。计算得：PW1=3.57 kN，PW2=4.87 kN，Mw=1 345.06 kN。

同时考虑重力荷载和附属钢梯影响，通过计算得到基本风速v10=5.4 m/s(距地面10 m高度的风速)时，风向角α与倒塌偏转角φ关系如图4所示。

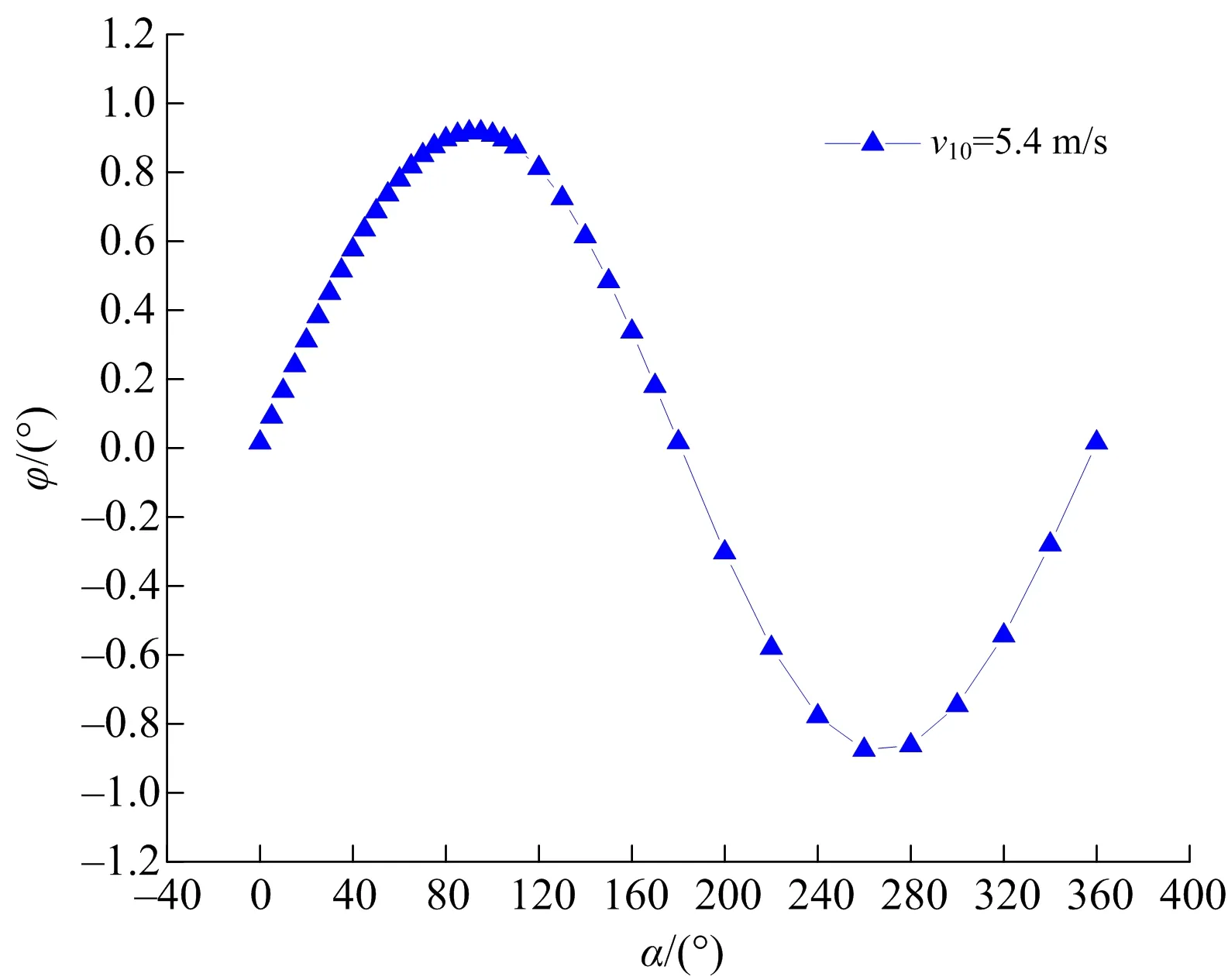
图4 风向角与倒塌方向偏转角关系Fig.4 Relationship between wind direction angle and collapse direction angle

可以看出，当基本风速一定时，倒塌偏转角随着风向的变化而改变；当预设倒塌方向逆时针旋转90°与风向一致时，对塔体倒塌方向影响最大。

3.2 风速对倒塌方向偏转角的影响

当基本风速不同时，作用于结构高度的风振系数βz也不同，基本风速v10与风振系数最大值βz max的关系如图5所示；顺风向风载作用下，基本风速与切口底部的风荷载弯矩Mw的关系如图6所示。

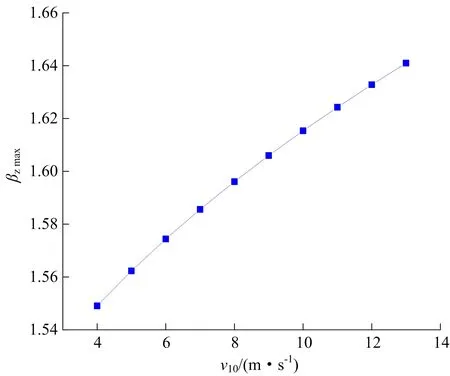
图5 基本风速与βz max关系Fig.5 Relationship between basic wind speed and βzmax

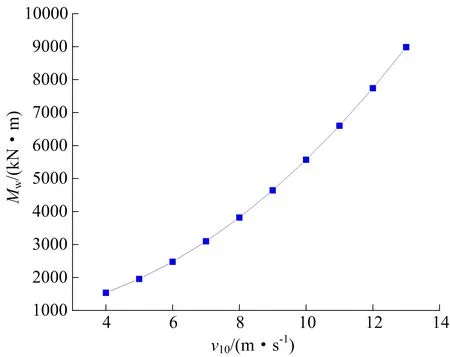
图6 基本风速与风荷载弯矩Mw关系Fig.6 Relationship between basic wind speed and Mw

随着基本风速的增加，风振系数最大值βz max和风荷载弯矩Mw皆呈现不断增大趋势，进而对电塔的倒塌方向产生影响。

这里进一步计算出了不同风速下风向角与塔体倒塌偏转角的关系(见图7)。

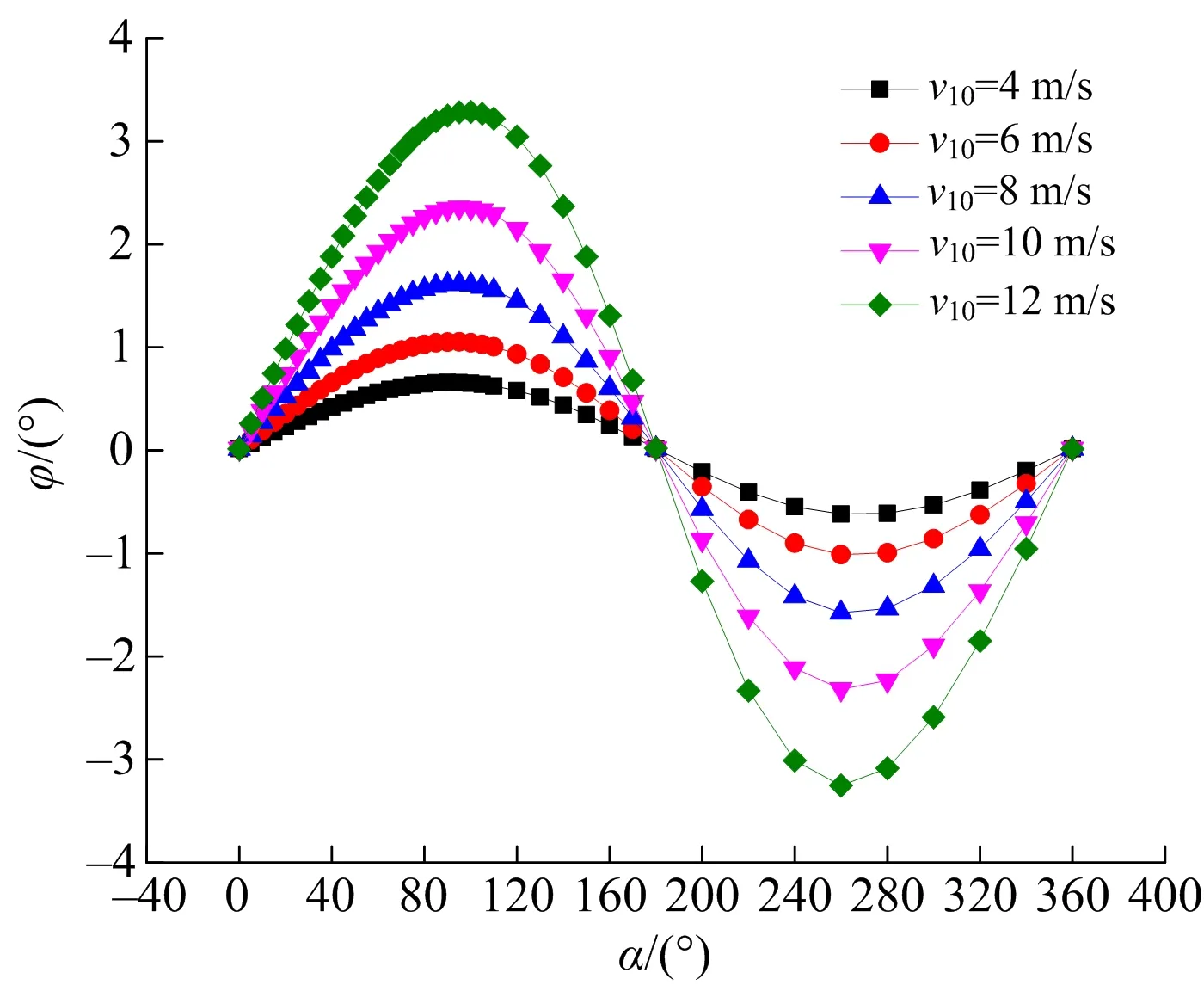
图7 风向角与倒塌方向偏转角关系Fig.7 Relationship between wind direction angle and collapse direction angle

塔体倒塌偏转角随着基本风速的增加而增大，且在风向角为100°时取得最大值。当基本风速在12 m/s以内时，塔体倒塌偏转角可控制在3.2°以内。

3.3 横风向风振效应对倒塌方向偏转角的影响

根据《建筑结构荷载规范》(GB 50009-2012)，当雷诺数Re≥3.5×106，且结构顶部风速的1.2倍大于临界风速时，即1.2vH>vcr，应验算共振响应。

雷诺数Re、临界风速vcr、结构顶部风速vH分别按照下式计算

Re=69 000vD

(13)

(14)

(15)

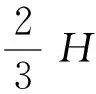
计算得到不同基本风速v10下，Re、vH和1.2vH数值如表1和图8所示。

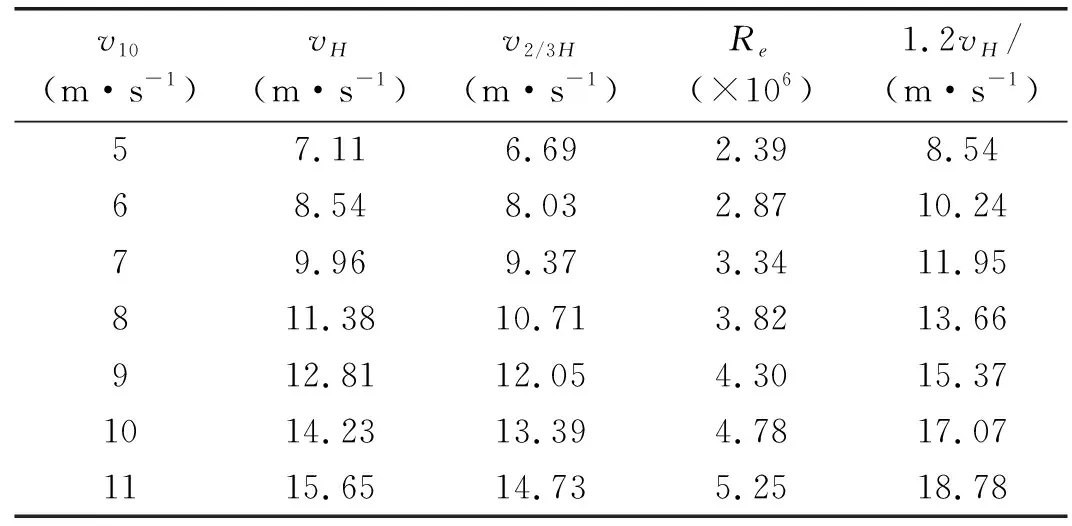
表1 不同基本风速下Re、vH和1.2vH数值表

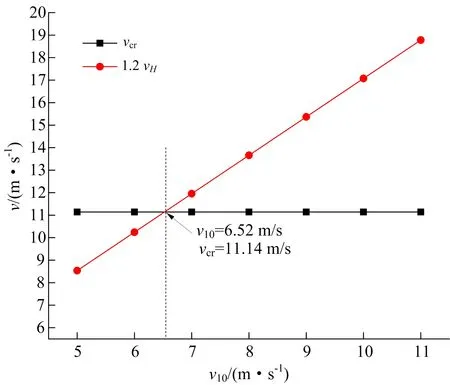
图8 不同基本风速下vcr和1.2vH关系Fig.8 Relationship between vcr and 1.2vH under different basic wind speeds

当1.2vH=vcr时，计算得到v10=6.52 m/s。因此，当基本风速v10>6.52 m/s时，适宜考虑横风向共振效应(跨临界范围的强风共振)对塔体的影响。

对跨临界的强风共振，在临界风速vcr起始点高度H1以上至1.3vcr一段范围内均为共振锁住区，基本风速均为vcr，存在以下关系

(16)

(17)

式中：H1为共振临界风速起始高度，m；H2为共振锁住区终点高度，当计算H2大于电塔高度时，取到结构顶点，m；α为与地面类型相关的系数，取0.15。

计算得到基本风速与共振锁住区高度的关系如图9所示。

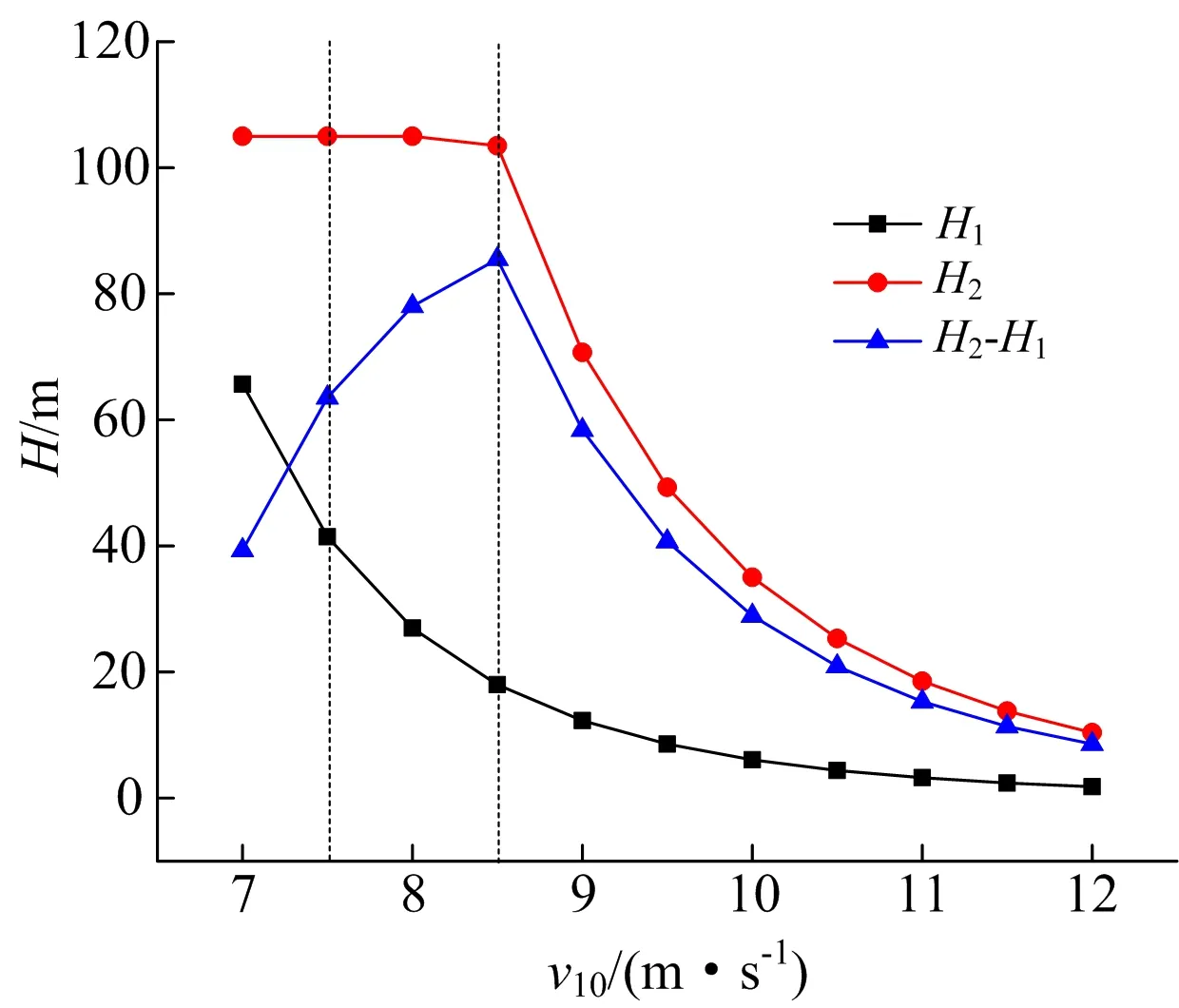
图9 基本风速与共振锁住区高度的关系Fig.9 Relationship between basic wind speed and the height of resonance lock zone

随着基本风速的增大，共振锁住区高度整体呈现逐渐减小趋势。当基本风速为7.5～8.5 m/s时引起的横风向共振效应最大；风速大于8.5 m/s后，共振锁定区下移，结构锥度增大，且振型系数小，可不考虑横风向共振影响。

横向共振引起的等效静风荷载计算公式为

(18)

式中：λj为计算系数；Φj(z)为结构的第j振型系数；ξj为结构的阻尼比，混凝土结构取0.05。

假定横风向沿结构高度均匀分布，分别计算得到不同基本风速下横风向风荷载产生的弯矩，然后得到横风向共振效应对倒塌方向偏转角的影响曲线(见图10和图11)。

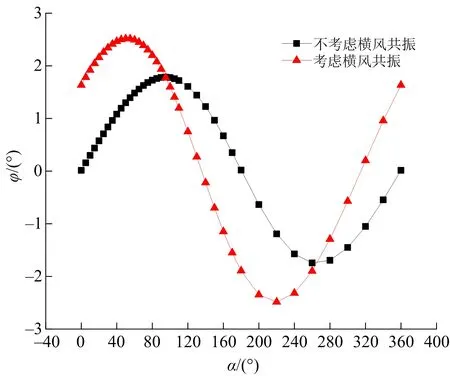
图10 v10=8.5 m/s时倒塌方向偏转角Fig.10 Deflection angle of collapse direction as v10=8.5 m/s

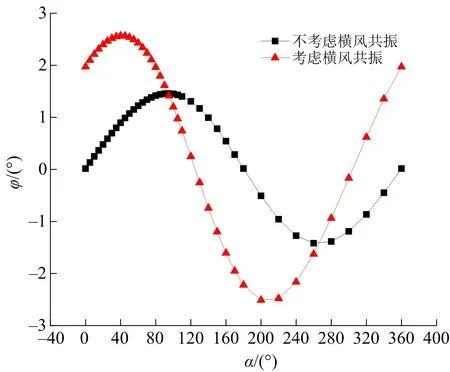
图11 v10=7.5 m/s时倒塌方向偏转角Fig.11 Deflection angle of collapse direction as v10=7.5 m/s

与顺风向风载效应相比，考虑横风向共振效应后，塔体的最大倒塌方向偏转角显著增加，引起最大偏转角的风向也出现显著变化。当风速在7.5～8.5 m/s时，横风向共振效应明显会使倒塌方向产生较大的偏转角，这里对应的风向角与预定方向并不在90°附近。

4 考虑风荷载爆破拆除方案及参数

根据电塔周边环境，为确保北塔拆除爆破安全，设计采用定向倒塌方案；倒塌方向与架线方向一致，南偏东56°。首先对跨越塔内部的钢梯进行预拆除，避免梯子对电塔的倒塌方向造成影响。然后按照设计的参数，在指定的位置开设定向窗和导向窗[10-12]，保证电塔倒塌方向的准确性。

图12 电塔内部钢梯Fig.12 Steel ladder inside the electric tower

图13 爆破定向窗Fig.13 Blasting directional window

根据工程实际经验并结合本工程特点，切口高度取3.6 m。设计爆破切口形状为正梯形，切口角度210°。设计钻孔直径D为40 mm；采用正方形布孔方式，孔距a×排距b=30 cm×30 cm。

采用复式非电导爆管起爆系统；以倒塌方向为中心，左右各分为3个区，延时对称起爆。

5 爆破危害效应控制及爆破效果

5.1 爆破危害控制措施

1)塌落振动控制。拆除爆破产生的振动效应包括爆破振动和建(构)筑物塌落的触地振动[13-15]，而通常后者的振动强度要比爆破振动大，且频率低，对四周民房等保护对象的危害也更大，因此，应以控制电塔倒塌触地振动效应为主。

为减轻电塔倾倒落地后引起的触地冲击振动强度，在倒塌方向上分别在距离电塔水平距离30、60、80、95 m处各设置一道缓冲墙，作为塌落冲击时的缓冲垫层。缓冲墙采用废旧轮胎堆筑，高度为1.2 m。

2)爆破飞散物控制。为有效控制爆破飞散物的危害，设计采用12层密目安全网对爆破切口进行覆盖防护，相邻防护网采用铁丝捆扎牢固，防止滑落。

5.2 拆除爆破效果

电塔拆除爆破效果如图14和图15所示。

图14 爆破倒塌过程Fig.14 Blasting collapse process

图15 爆破倒塌效果Fig.15 Blasting collapse effect

现场实测表明，电塔附近的基本风速在4～7 m/s；通过严格控制爆破参数、切口高度、起爆网路等，成功实现了电塔的定向爆破倒塌，消除了电塔安全隐患。现场实测表明，现场爆破后电塔按照设计倾倒方向进行倒塌，电塔实际倾倒偏转角度在理论分析范围内，较好地验证了理论分析的可靠性。

通过爆破安全防护，爆破飞石控制在30 m以内，周边民房等完好无损；现场监测显示，距离电塔90 m和170 m处的最大振动速度分别为1.38 cm/s和0.59 cm/s，振动速度在周边设施的安全范围内。

6 结语

1)风荷载对电塔偏转角影响分析是指导现场拆除爆破的重要理论依据。研究表明，倒塌偏转角随着风向的变化而改变，当预设倒塌方向与风向一致时，对塔体倒塌方向影响最大。塔体倒塌偏转角随着基本风速的增加而增大，且在风向角为100°时取得最大值。

2)当基本风速为7.5～8.5 m/s时，横风向共振效应会引起较大的倒塌偏转角，需要注意的是对应的风向角与预定方向并不在90°附近。当风速小于7.5 m/s或大于8.5 m/s时，可不考虑横风向共振效应的影响。

3)通过精心设计、施工，现场爆破后电塔按照设计倾倒方向进行倒塌，实际倒塌偏转角度控制在理论分析范围内，较好地验证了理论分析的可靠性。