基于模糊PID控制的工程车辆机械液压控制策略研究

阚玉锦,苏 进,丁响林

(安徽机电职业技术学院 机械工程学院,安徽 芜湖 241002)

近年来，国家对基建施工的质量、环保与安全的要求越来越严格，传统工程车辆的机械液压控制方法已经不能满足当下高标准的需求[1].比如传统的PID控制算法，虽然具有部署及运用简单等优点，而且在大多数机械运动控制系统里，其控制效果已经足够满足工程要求，是目前工程上使用最为广泛的控制算法，但是该算法具有在某些情况下不能忽视的缺陷.比如对被控对象的数学模型依赖程度大，对非线性对象控制效果不佳等.行业相关研究多倾向于对车辆本身部件进行改进来优化控制效果，此种方式成本较大.因此，从现有方法进行改进以提高对工程机械的控制效果，有一定研究价值[2].

1 基于模糊PID控制的工程车辆机 械液压控制方法设计

1.1 模糊PID控制算法构建

在工程建设领域，很多有特殊作业要求的工程车辆机械，比如需要保证行驶稳定的路面摊铺机、沥青洒布车、路面铣刨机等[3].然而，由于施工现场的各种不确定因素和负载的随机性、系统性波动，传统的控制方法已经难以满足对工程车辆稳定行驶的控制需求[4-7].针对这一矛盾，前人提出过多种解决方案，比如使用PID控制，虽然运用广泛，但在某些情况下也有不能忽视的缺陷[8]，控制效果受部件的数学模型质量好坏影响程度大，泵控马达速度控制系统在一般情况下具有延迟性，作用机理复杂，且工作过程中状况复杂多变，因此难以使用数学建模方法将其核心工作流程抽象提取出来，导致PID控制算法无法快速准确地达到控制要求[9-11].

新兴的智能控制技术为解决这类难题提供了新思路，特别是其中的模糊控制法，其鲁棒性、稳定性优良，对内在规律复杂或无法用数学语言描述的非线性复杂系统控制效果较好.但它无法消除系统稳态输出值与目标值的偏差，基于此问题，本文研究将PID控制算法与模糊控制法融合来优化工程车辆的行驶稳定度[12]，构建模糊PID控制算法.PID控制中，设置期望值与反馈值的差值为e(t)，为适应计算机计算而离散化处理后的控制量u(t)表达式如式(1)所示.

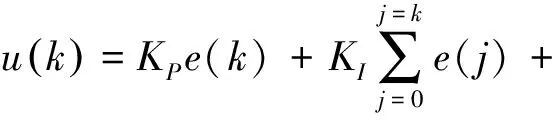
(1)

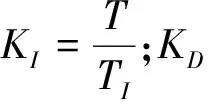
式(1)因为控制器的输出与被控制对象的实际位置相互对应，也被称为位置式PID，该特点导致控制器一旦出错，就容易造成误动作，甚至产生工程事故.为避免此缺点，需要对算法进行改进.为进一步简化计算过程，提高序列计算效率，公式(1)还可被改写成公式(2).

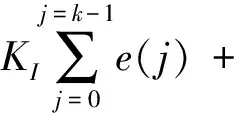
(2)

再将公式(2)减去公式(1)，即可得到增量式PID，如公式(3)所示.

Δu(k)=KP[e(k)-e(k-1)]+KIe(k)+KD[e(k)- 2e(k-1)+e(k-2)].

(3)

因此也可得出增量式PID控制器的输出表达式：u(k)=u(k-1)+Δu(k).对比增量式与位置式PID，可发现，两者在形式有较大区别，前者不存在积分操作，因而不会引起积分饱和，也就不需要对积分进行限幅，输出计算的限幅即可.退一步分析，即便计算器运行出错，由于控制器输出对应着对象位置的变化量，误动作造成的影响也会比位置式PID小.为了消除控制系统运行时产生的稳态误差，大多数情况下还需要引入积分操作，由于控制器输出还会受到PWM占空比极值影响，所以需要对PID控制器输出做限幅处理，设控制器输出的上下限值分别为umax和umin，则添加限幅操作后的控制器输出值如公式(4)所示.

(4)

模糊控制法是通过把专家的经验总结并转换为计算机程序，即模拟人的思维方式来对对象进行控制的方法[13-14].其对内在规律复杂或无法用数学语言描述的非线性复杂系统控制效果较好，工作原理如图1所示.

由图1可知，模糊控制法的核心思想就是制定模糊控制命令，其依据是行业相关专家的成熟经验，首先把模糊关系R通过相应计算规则解出，同时通过传感器得到当前计算指标的测量值，根据两者计算出偏差值e；再使用R把e转换为模糊量E，结合运算规则对E进行推理，从而求出控制量U=E°R；最后对U使用反模糊规则转化为一个精确的控制量u，发送给被控对象以执行相应控制操作.模糊控制也存在控制精度低、自适应能力有限等缺点，所以将增量式PID算法与模糊控制法融合起来，融合后的算法流程如图2所示.

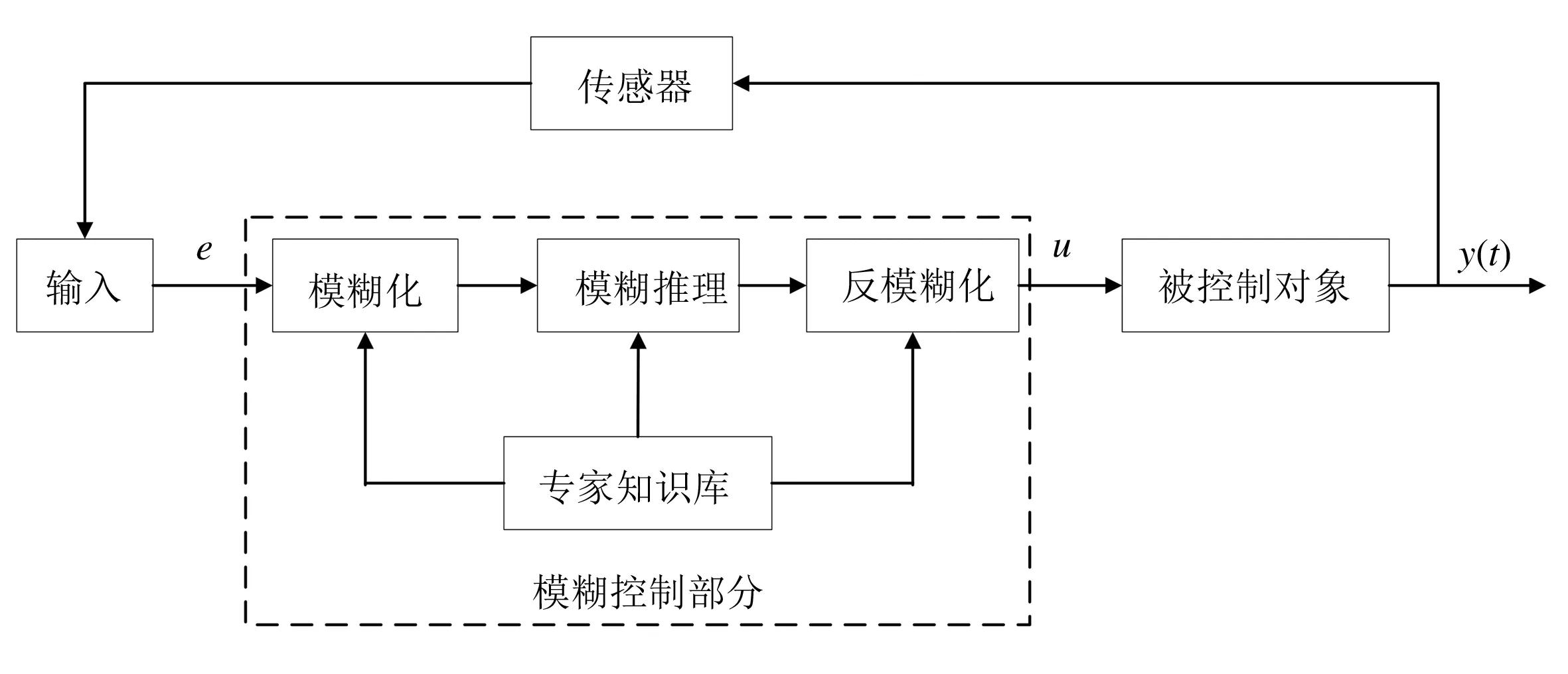
图1 模糊控制法工作原理

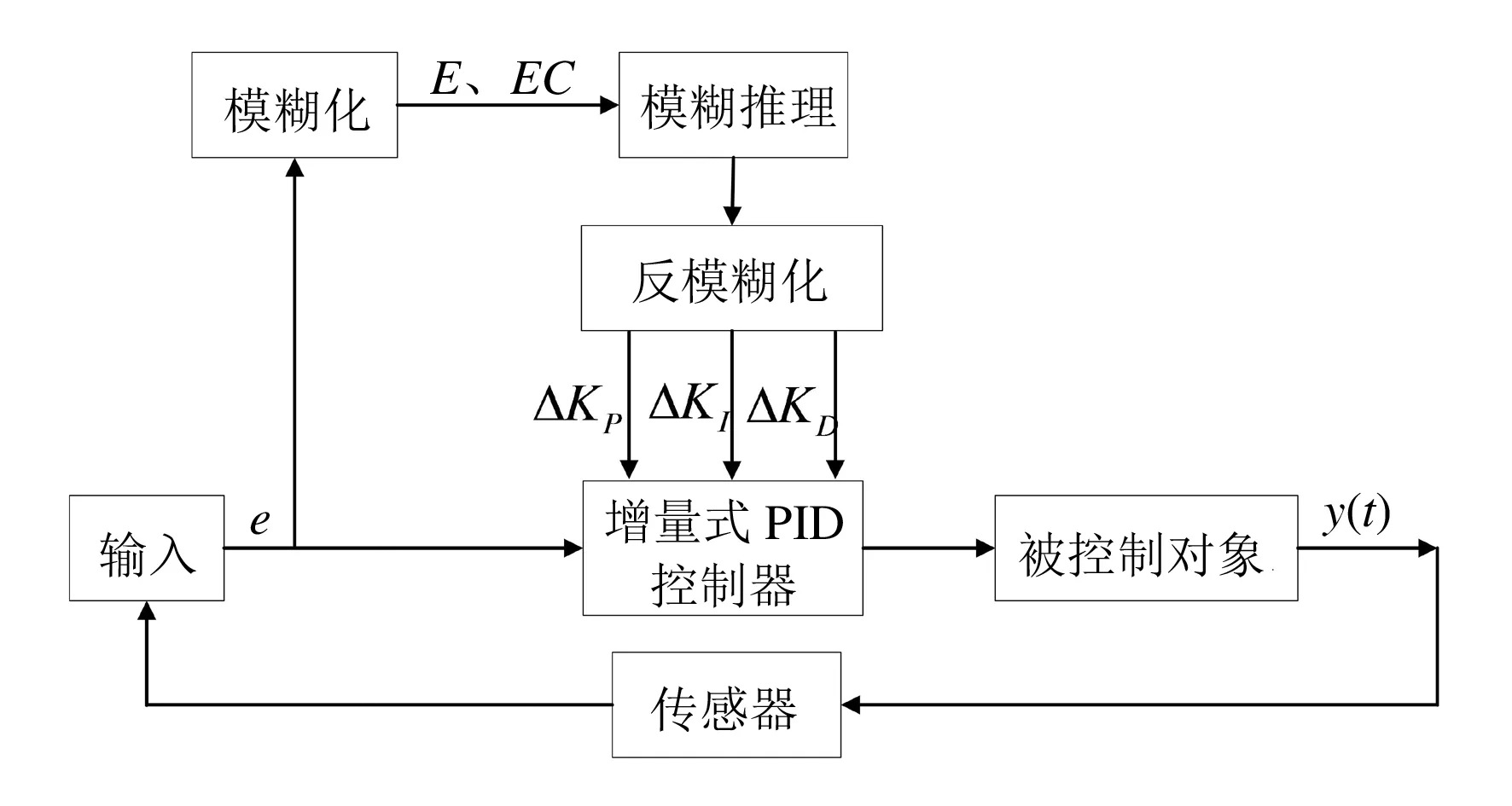
图2 模糊PID算法的计算流程

由图2可知，模糊PID控制器由PID控制器和模糊控制器两部分组成，其核心思想是先将专家的PID参数转化为模糊规则存入MCU部件，然后MCU通过实时误差及其变化率将PID参数更新，达到让被控对象运动更加稳定、流畅的目的.

1.2 工程车辆机械液压控制系统的数学模型 构建

由于模糊PID算法的计算效果会受到研究对象的数学模型影响，因此本文主要以工程车辆机械液压系统中的常见部件，即泵控马达速度控制系统为对象，构建其数学模型.泵控马达速度控制系统由三大核心组成部分，分别为速度传感器、泵控马达系统和变量机构，下面分别构建其数学模型[13-14].先对电液比例变量机构建模，电液比例变量机构的比例放大器电流I对偏差电压E的传递函数、阀芯位移Xv对电液比例换向阀电磁铁线圈电流Ibv的传递函数如公式(5)所示.

(5)

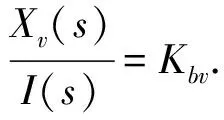
(6)

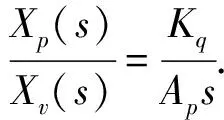
(7)

其中，Kqp为变量泵的流量增益(m3/s·rad)；Dm为马达的排量(m3/rad)；V0为液压回路的有效容积(m3)，Ct为系统总泄露系数(m5/N·m)；ωh为液压固有频率(rad/s)；ζh为液压阻尼比；βe为有效体积的弹性模量(Pa).

(8)

其中，Kf为反馈增益系数(V·s/rad).完成泵控马达速度控制系统数学模型搭建后，就可形成完整的基于模糊PID控制的工程车辆机械液压控制系统，该系统一般结构由控制器、模式切换、车速控制、发动机转速控制和人机交互系统5大核心部分组成.其中控制器负责对各种输入信号处理、实现对系统的控制，其核心就是本文提出的模糊PID控制算法.

2 基于模糊PID算法的工程车辆机 械液压控制仿真实验分析

为了验证模糊PID算法对工程车辆机械液压控制系统控制的车辆行驶稳定性优化效果，本设计选取在工程车辆市场上具有一定代表性的SX1254BM434型载货汽车的车辆底盘为研究对象，并选用TMS320F28335型32位浮点DSP处理器，结合建立的数学模型，采用MATLAB编写脚本进行工程车辆行驶稳定性的仿真实验.仿真实验中涉及参数的值如表1所列.

表1 仿真试验参数表

根据表1所列数值设置好实验所需各参数后，再结合数学模型使用MATLAB建立工程车辆行驶的仿真系统.在实际工程现场中，工程车辆常用一档来进行行驶移动，且常常会受到各种负载干扰.因此仿真实验也以一档为行驶条件，将其行驶速度设置为2 km/h，同时将在行驶4 s后对其作用一个大小500 N·m的负载干扰信号.运行实验并整理数据后得到改进算法与原始算法控制下的速度阶跃相应曲线，结果如图3所示.

由图3可以发现，在起步加速阶段，使用传统PID算法控制，系统速度达到峰值耗时0.82 s，最大超调量为13.36%，调整到设定速度耗时2.23 s，而使用模糊PID算法系统，速度达到峰值耗时0.83 s，与PID控制相差不大，最大超调量6.94%，比PID控制减少了48.05%，稳定耗时1.78 s，比PID控制算法缩短了20.18%.在负载作用阶段，使用传统PID算法时，系统的调整耗时是1.46 s，速度最大超调量为13.52%，而采用模糊PID算法时，系统调整耗时1.07 s，速度最大超调量为8.11%，分别比前者减少了26.71%和40.01%.以上数据充分说明，采用模糊PID控制算法比起传统PID算法，能明显提高系统的稳定性和反应速度.使用模糊PID控制时，车辆加速快慢对行驶稳定性的影响情况如图4所示.图4为采用模糊PID算法时，分别加速0.6 s、0.8 s、1.0 s和1.2 s达到1档设定的速度响应曲线.

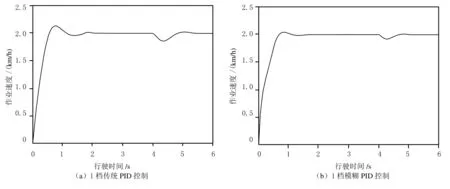
图3 车辆行驶时有负载扰动的速度阶跃响应曲线

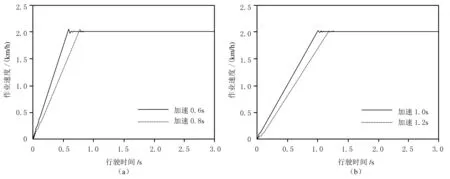
图4 不同加速时间下系统的速度响应曲线图

由图4可知，加速时间为0.6 s、0.8 s、1.0 s和1.2 s时，车辆速度从加速完成到稳定状态耗时分别为1.22 s、1.27 s、1.31 s、1.36 s和1.40 s，超调量分别为3.3%、2.8%、2.2%和2.7%.容易看出，加速时间越长，速度波动越小，行驶越平稳，但加速时间也不宜过长，否则会影响施工效率，应该结合工程的具体情况设置合适的加速时间.

3 结论

针对工程车辆机械液压的控制问题，本文提出了一种融合模糊控制与PID控制的混合模糊PID控制算法，将输入信号先输入模糊控制器处理，再反模糊化输出给PID控制器实现两者的融合.为了验证算法的有效性，选取工程车辆机械液压系统中的常见部件，泵控马达速度控制系统对其构建数学模型.以SX1254BM434型载货汽车的车辆底盘和TMS320F28335型处理器硬件数据为基础，通过MATLAB进行仿真实验.实验结果显示，在起步加速阶段，使用模糊PID控制算法，系统最大超调量6.94%、稳定耗时1.78 s，分别比PID控制算法的减少了48.05%与20.18%.在负载作用阶段，使用模糊PID控制算法，系统调整耗时1.07 s，速度最大超调量为8.11%，分别比传统PID控制算法减少了26.71%和40.01%.实验证明，采用模糊PID控制算法比起传统PID算法，能明显提高工程车辆的变速与行驶稳定性.