深度学习算法在颗粒状农产品品质分选中的应用研究

王艳兵

(徽商职业学院 电子信息系,安徽 合肥 230000)

借助机器视觉技术，能够对农业产品中外表破损、颜色改变的产品进行检测，进而区分出合格与不合格的产品[1-2].在传统的色选系统中可以筛选的物料有限，可以使用的范围比较窄，有一定的局限性.此次研究的对象为颗粒状农产品中的花生.对花生进行色选，往往面临着花生容易发生霉变，导致表面易破损、断裂等问题[3].随着计算机和嵌入式技术的不断发展完善，本文基于深度学习中的色选图像分类算法，以花生为对象组成了图片数据集，构建了卷积神经网络，并进行了优化设计，实现了对颗粒状农产品的图像分类，减少了准确率波动，有效提高了优化算法在颗粒状农产品品质分选中的准确率.

1 深度学习算法在颗粒状农产品品 质分选中的应用

1.1 颗粒状农产品品质色选图像分类算法

选择花生作为颗粒状农产品中的研究对象，在彩色色选系统中构建两个数据集，并应用图像分类算法进行产品筛选[4-5].第1个数据集总共包含407张花生图像，分为完好花生、半个花生和表皮破损花生3类标记标签.将做好分类标记标签的数据按照8∶2的比例分为训练集和测试集，其中训练集为325张花生图片，测试集为82张花生图片，图1展示了部分训练集的花生图片.上面一排是完好花生，中间一排是表皮破损花生，下面一排是半个花生.

第2个数据集总共包含350张花生图片，分为表皮破损区域小于阈值、临近阈值和大于阈值3类标记标签.和第1个数据集一样，将做好分类标记标签的数据按照8∶2的比例分为训练集和测试集，其中训练集为280张花生图片，测试集为70张花生图片，图2展示的是部分训练集的花生图片.上面一排是远小于阈值的表皮破损区域花生，中间一排是远大于阈值的表皮破损区域花生，下面一排是临近阈值的表皮破损区域花生.

图1 第1个数据集集中训练集部分花生图片

图2 第2个数据集中训练集部分花生图片

构建本文卷积神经网络(CNN)的结构，网络各层由1个输入层、4个卷积层、4个池化层和3个全连接层组成.CNN的输入层输入3个尺寸为100×100的花生图片，卷积层经过SAME边界补0的方式进行处理，在4次卷积之后深度加深，但花生图片的长和宽保持不变[6].CNN的池化层经过VALID边界不补0的方式进行处理，同时将步长设置为2，在4次池化之后深度不变，但减少了花生图片的长和宽.由上述可知，4次卷积和池化的花生图片变化尺寸为：

100×100×3→100×100×32→ 50×50×32→50×50×64→ 25×25×64→25×25×128→ 12×12×128→12×12×128→ 6×6×128

.

通过转化为一维6×6×128三个全连接层后输出，这时数据转变为6×6×128→1024→512→3.通过softmax分类器能够将一维中的数值转化为[0,1]及和为1的对应概率，将3类数据中输出的一维向量借助softmax分类器进行传递.研究假设有K(K=3)个类别，经softmax分类器计算，具体如公式(1)所示.

(1)

式(1)中，Zj代表的是一维向量在连接层输出后的第j+1个数值.

比较标准标签和输出标签中损失函数的大小，借助softmax计算得出.然后对各层参数的数值进行调整，从而不断减小损失函数，神经网络得以进一步改进优化.研究中使用的是交叉熵分类损失函数，具体公式如式(2)所示.

(2)

从式(2)可以得知，这组数据通过softmax为log函数内部的值输出正确的分类值，从中得出的值与损失函数值呈反比关系，满足损失函数的要求.以花生图片1的数据集为参照，训练在CPU+GPU上构建的CNN，采用55张图片对CNN进行训练，也就是说batch设置为55，学习率设为0.0001，经过40次的迭代后，花生的分类准确率能够达到 90.91%，较为稳定.此次研究采用8-5-3结构的神经网络来验证CNN的效果，在数据集上学习100次进行训练测试，其花生的分类准确率为85.45%，因此，基于颗粒状农产品的分类算法能够高效完成花生的分类，提高正确率.

1.2 颗粒状农产品品质分选中算法的优化设计

对颗粒状农产品进行品质分选方面，研究该卷积神经网络算法中过拟合、指数衰减法设置学习率、滑动平均模型以及最终综合方案的优化和改进.对于一个异常复杂的模型，过拟合通过对每一个训练数据中的部分随机噪音进行记忆，使其忘记去“学习”训练数据，虽然在训练中的模型表现优良，但是在预测效果方面则相对较差.为了避免过拟合现象，此次算法的优化采用正则化方法，其思想是在损失函数上增加复杂模型的指标.假设在训练数据上增加复杂模型的损失函数用J(θ)来表示，那么它会优化J(θ)+λR(ω)，而非直接对J(θ)优化.这里的权值向量用ω来表示，增加模型的两种复杂程度用R(w)来表示，其中R(w)存在两种形式，经过L1和L2正则化，具体计算见公式(3)和公式(4).

(3)

(4)

根据公式(3)和(4)可知，在总损失中模型复杂损失的比例用λ来表示，令λ=0.1，从而使L1和L2正则化的效果达到对权值向量ω的限制，两者皆是通过限制ω的大小来使模型不能对训练数据任意拟合.由上述计算结果可知，与L1正则化相比，L2正则化在优化时公式可导，且损失函数的优化比较简洁，L2正则化在建立的数据集上更加有效地提高了颗粒状农产品的分类准确率，因此在改进卷积神经网络算法中选用L2正则化.

在训练过程中，CNN采用梯度下降算法来对网络参数进行优化[7-8].其中学习率作为该算法的重要参数，网络参数移动到最佳值的快慢由学习率的数值大小决定，且优化率和学习率呈正比.研究对学习率的设置是通过指数衰减方法来进行的，为了得到最佳解，需要用一个比较大的学习率，当迭代次数不断增加时，进一步减少学习率，从而使处于后期的训练次数在模型中更加趋于稳定.当迭代次数变化，学习率的计算具体见公式(5).

(5)

其中，n表示迭代次数，θ表示衰减速度，λ表示在优化时使用的学习率，λ0表示数值为0.001的初始学习率，ε表示数值为0.99的衰减系数，且0<ε<1.

为了降低数据训练中噪音对模型造成的影响，本优化算法采用滑动平均模型来加快收敛速度，具体计算见公式(6).

θn+1=(1-β)θ+βθn，

(6)

其中，β为衰减率，且0<β<1，θ表示迭代输入值，θn代表上次迭代后输出结果，θn+1代表本次迭代后输出结果.这里β对模型的更新速度有决定作用，并在此基础上引入num_updates参数，实现对衰减率β的动态设置.

该优化算法应用在色选系统中，还需要实时判断和处理传送的物料[9-10].由于此次把花生作为研究对象，筛选出的物料图像比较简单，因此还可以对深度学习算法下的CNN进行简化操作，经过简化之后的网络结构如图3所示.

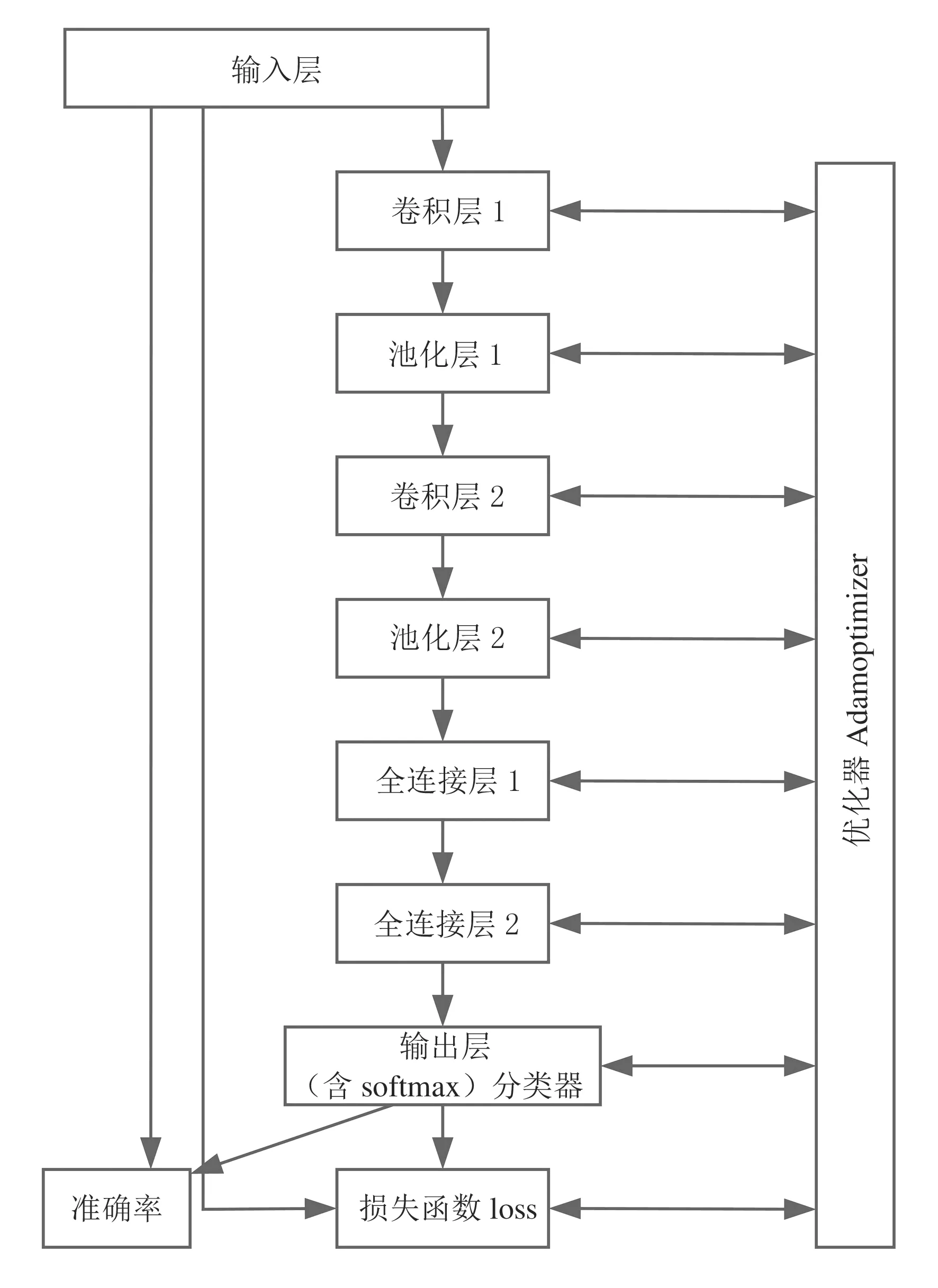
图3 简化后的神经网络结构图

从图3可以看出，与之前构建的神经网络相比，优化后的神经网络由1个输入层、2个卷积层、2个池化层和2个全连接层组成.对2个池化层和卷积层进行计算，这时的尺寸变化为：

100×100×3→100×100×32→ 50×50×32→50×50×64→ 25×25×64

.

通过转化为一维25×25×64两个全连接层后输出，这时数据转变为25×25×64→1024→3.经计算，在训练过程中，简化后的神经网络需要将池化层和卷积层的参数加以优化，总共有：

(5×5×3+1)×32+32×2+ (5×5×32+1)×64+ 64×2=53888个，

与优化前相比，整体上降低了80%，极大地节约了训练和测试所需的时间.

2 颗粒状农产品品质分选的应用结 果分析

在颗粒状农产品品质分选方面，以花生为例，对卷积神经网络中的优化结果加以分析.首先对算法中的数据集优化结果进行分析，将预测数据收集到的407张图片分别进行编号测试.在测试的花生图片里，分类错误的花生图片详见图4(a)，从下至上按照1—5进行排序，1号花生破损命名为半个花生，2号花生破损命名为完好花生，3号花生完好命名为半个花生，4号完好花生命名为破损花生，5号半个花生命名为破损花生.将标记错误的图片放入到数据集中训练，从图4(b)可以看出，对比数据集1在优化改进前后10次的变化，可以看出整体的趋势一直处于稳步上升状态，除了第4次和第7次准确率高于改进后，剩余的8次改进优化后的准确率都要远远高于改进前的准确率.

根据过拟合、指数衰减法和滑动平均模型3个方面优化的结果可以看出，图5(a)在数据集1中，对改进前、L1正则化、L2正则化准确率的情况进行测试.L1范数经过正则化，与原始准确率相比，初期数值虽呈下降趋势，但当增加训练次数时，准确率开始较为稳定且呈现不断上升的态势，减少了过拟合现象.数据经过L2正则化，与原始准确率相比有显著提高，并且当训练次数不断增加时准确率呈现单调上升.数据经过正则化之后，较好地缓解了过拟合，有效提高了颗粒状农产品品质分类的准确率.

采用tf.train.exponential_decay和TensorFlow函数进行编程，以达到指数衰减的目的.在数据集1上将优化前后的测试集分类进行对比，从图5(b)中可以看出，由于先设置了一个比较大的学习率应用于指数衰减法，在1—9的训练次数里优化算法的准确率增幅较大，随后训练次数增幅较小，这是因为学习率随着迭代次数的增加而减少.在进行1—20次训练后，分类准确率能够达到98.18%，优化效果良好.比较滑动平均模型优化前后分类准确率情况，从图5(c)中可以看出，选择1—20个训练次数，在前期1—10的训练次数中，分类改进优化后的准确率明显低于改进优化前，由于滑动平均模型使网络结构的稳定性增加，在剩余的10次训练过程中，改进优化后的正确率高于改进前，减少了改进优化后的准确率波动.

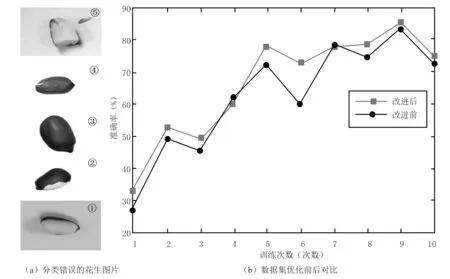
图4 分类错误的花生图与优化前后的数据集对比

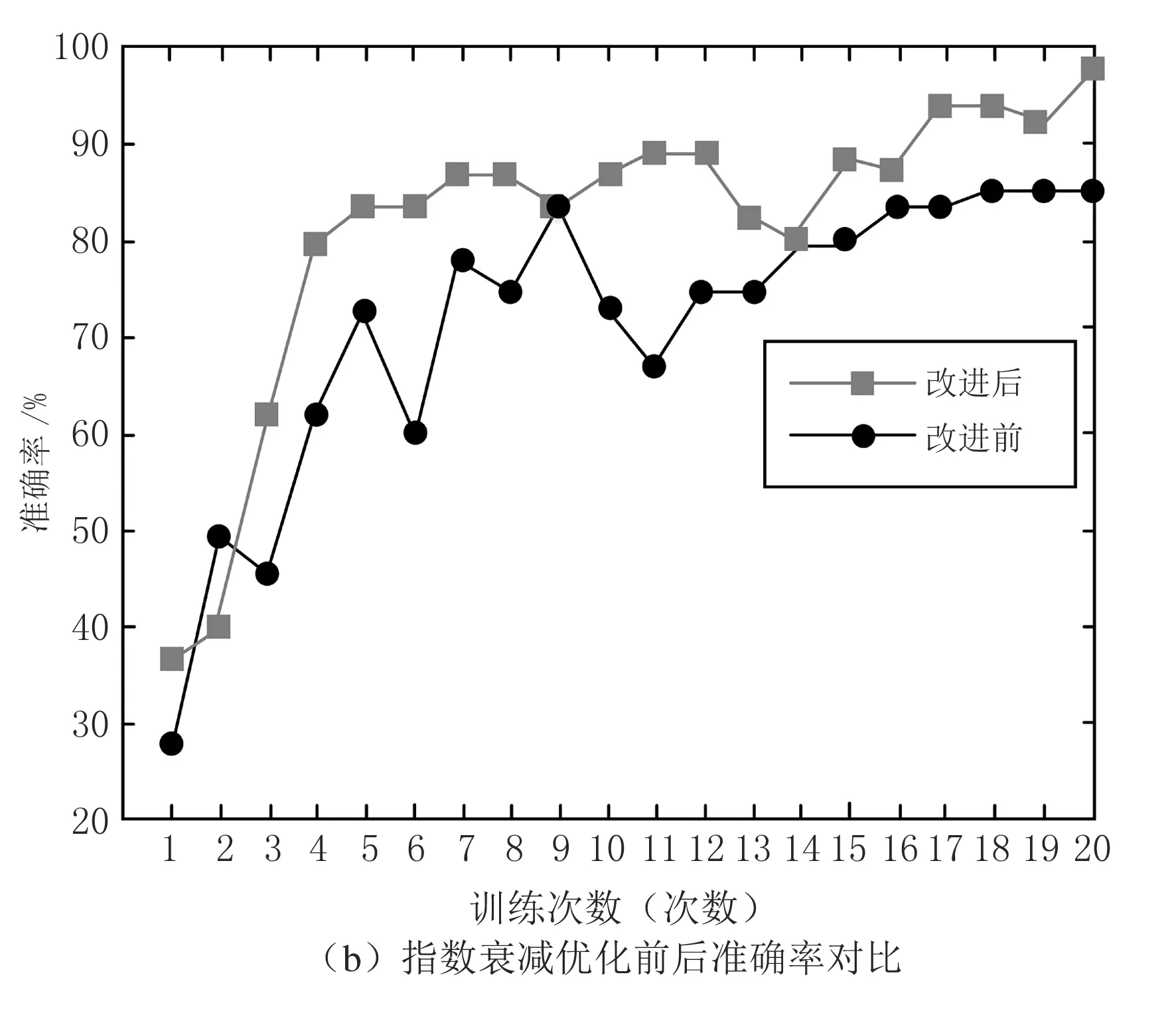
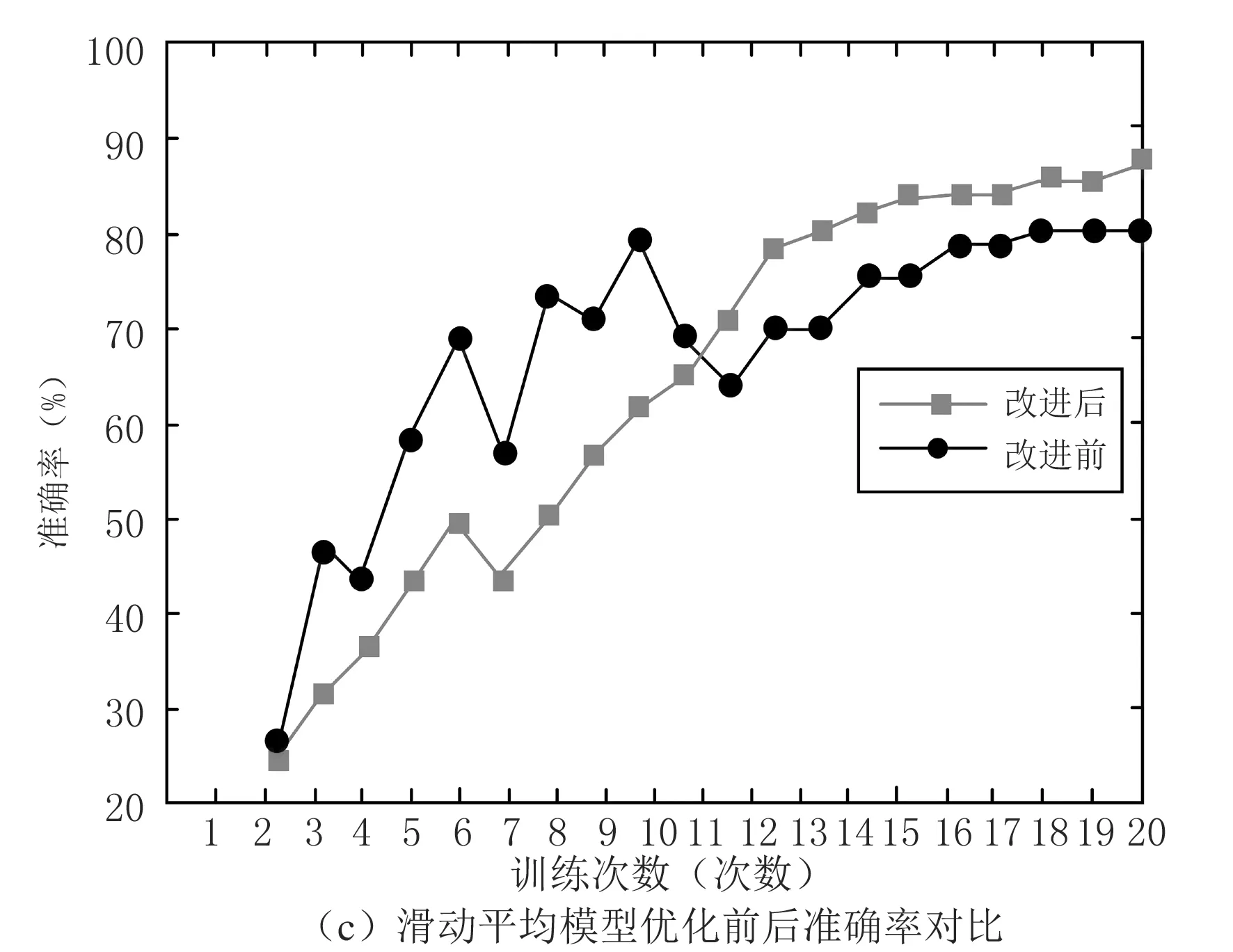
图5 花生品质分类算法优化对比

研究所采用的方案最终是正则化L2、数据集、滑动平均模型和简化网络结构指数衰减学习率综合作用下的优化.最终的优化卷积神经网络算法与之前构建的卷积神经网络算法比较结果如图6所示，从图6(a)中可以看出，选取1—43次进行训练，在测试集上对数据集1分类的准确率加以对照，当训练在37次之后，准确率高达98.18%，改进后的优化分类的准确率显著提高，同时呈现稳步上升的态势.在数据集2上对改进前与改进后的卷积神经网络进行训练和测试，这时将batch设置为55，从图6(b)中可以看出，在测试集上对数据集2的分类的准确率加以对照，同样选取1—43次加以训练，其数据在训练5次后准确率为95.64%，且较为稳定，提高了改进优化后分类准确率，满足对颗粒状农产品品质色选系统的性能需求.

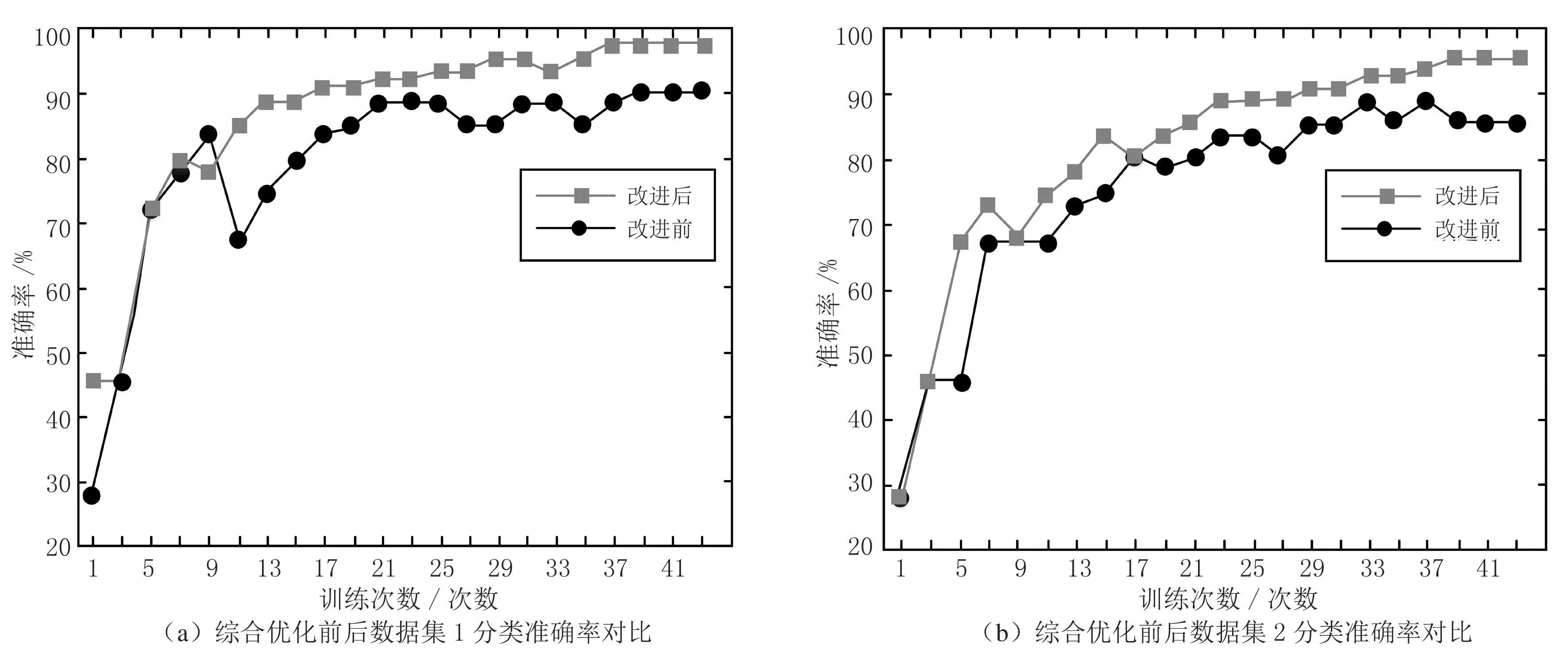
图6 数据集1与数据集2综合优化前后分类准确率优化

此外，在数据集1中，将407张花生图片应用于改进前的卷积神经网络算法，并对其进行测试，需要的时间为12.51 s.当407张花生图片应用于改进后的算法测试所需要的时间为7.44 s，也就是说，每一张花生图片的处理的平均用时仅需要18 ms.在数据集2中，将305张花生图片应用于改进前的卷积神经网络算法，并对其进行测试，需要的时间为14.33 s.当350张花生图片应用于改进后的算法测试所需要的时间为8.18 s，也就是说，每一张花生图片的处理的平均用时仅需要23 ms.由此可知，无论是数据集1还是数据集2，都能满足颗粒状农产品品质色选设备实时性的要求.

3 结论

传统的颗粒状农产品品质分类存在筛选效果差、分类效率低等问题，无法满足农业加工领域的需求.鉴于此，为了对颗粒状农产品的品质进行精确分类，以颗粒状农产品中的花生为例，将深度学习算法应用于对农产品的品质分选，构建了花生图像库1和图像库2，从正则化L2范数、滑动平均模型、设置指数衰减法的学习率和过拟合等方面考虑，搭建了优化卷积神经网络.研究结果表明，指数衰减后的学习率能够达到98.18%，卷积神经网络在进行优化后的准确率达到95.64%，同时卷积神经网络通过正则化减少了过拟合，在训练中的收敛速度也有所提升，提高了颗粒状农产品的分类准确率，满足了对颗粒状农产品品质分选需求，该优化算法方案很好地完成了预期目标.此次研究虽然取得了一定的成果，但仍存在一些不足，今后将研究不再局限于颗粒状农产品的品质分选，拓宽对其他农业产品的研究与应用.