基于距离偏差因子的WSN参考点迭代定位算法

陈 静，夏 超

(安徽理工大学 电气与信息工程学院，安徽 淮南 232001)

为了在工程应用中提供精确的监控服务，必须要应用WSN节点位置的相关信息[1-2].WSN中有多种目标节点的定位算法，基于RSSI测距的定位算法因其成本和能耗低等优点被广泛采用[3].

然而，WSN中RSSI信号传输噪声严重影响了目标节点的定位精度，引起相关领域专家和学者的广泛关注.文献[4]提出了一种三角形质心定位算法(Triangle Centroid Positioning, TCP)，该算法没有充分考虑节点分布特性，定位误差比较大.文献[5-6]提出了一种改进加权质心定位算法(Weighted Centroid Positioning, WCP)，该算法在距离估计过程中存在偏差，易产生较大定位误差.文献[7-8]提出了一种基于RSSI信号指纹数据库的定位算法，该定位算法高度依赖指纹数据库数据，一旦环境发生变化，定位精度会明显下降.文献[9]提出了一种基于神经网络的定位算法，该算法学习规则简单，在数据不充分的情况下，会产生明显的定位误差.针对单一定位算法定位精度低的问题，研究人员提出了融合定位的解决方案.文献[10-11]提出了一种将行人航位推算法与RSSI融合的定位算法；文献[12-13]提出了将惯性测量单元和超宽带测距测量融合的定位方法；文献[14]提出了一种将惯性测量单元与远程WiFi和短程超宽带测距测量融合的定位方法.然而，上述融合定位方法需要额外的设备，对硬件的成本要求较高.

针对上述问题，为了提高节点的定位精度，同时又不增加硬件成本，本文提出用距离偏差因子对参考点进行迭代定位，获得了目标节点的精确定位坐标.

1 基于RSSI的测距算法

RSSI测距算法是通过测量接收到的RSSI信号来计算目标节点和信标节点之间的距离.目前常用的测距模型是对数-距离路径损耗(Log-Distance Pass Loss, LDPL)模型，其表达式如式(1)所示.

P(d)=P(d0)-10nlog10(d/d0)+Xσ，

(1)

式(1)中，n表示路径损耗因子；X为阴影系数，是一个以0为均值、以σ为方差的高斯随机变量；P(d)为两个节点之间距离为d时的RSSI值；P(d0)为两个节点之间距离为d0时的RSSI值，其中d0为参考距离，一般取1 m.

当d0取1 m，并用RSSI表示d处的信号强度时，式(2)可简化为：

RSSI(d)=A-10nlog10(d)+Xσ，

(2)

式(2)中，A是节点间距为1 m时的RSSI标准值.

2 参考点迭代定位算法

在实际的物理环境中，信号在传输过程中很容易受到噪声的干扰.因此，由LDPL模型获得的距离与真实距离值之间存在较大偏差.为了进一步减小定位误差，引入了参考点迭代定位算法(Iterative Positioning Algorithm of Reference Point, IPAoRP).该算法首先基于所测得的距离分别计算位于3个定位圆重叠部分弧上的3个参考点坐标，以3个参考点的质心作为目标节点的初始定位坐标，其次引入距离偏差因子重新计算节点间距离，基于新的距离反复迭代参考点坐标，更新目标节点的定位坐标，直到满足迭代准则.

2.1 参考点坐标的计算

参考点的计算原理图如图1所示，以参考点A1(xr1,yr1)的计算为例.

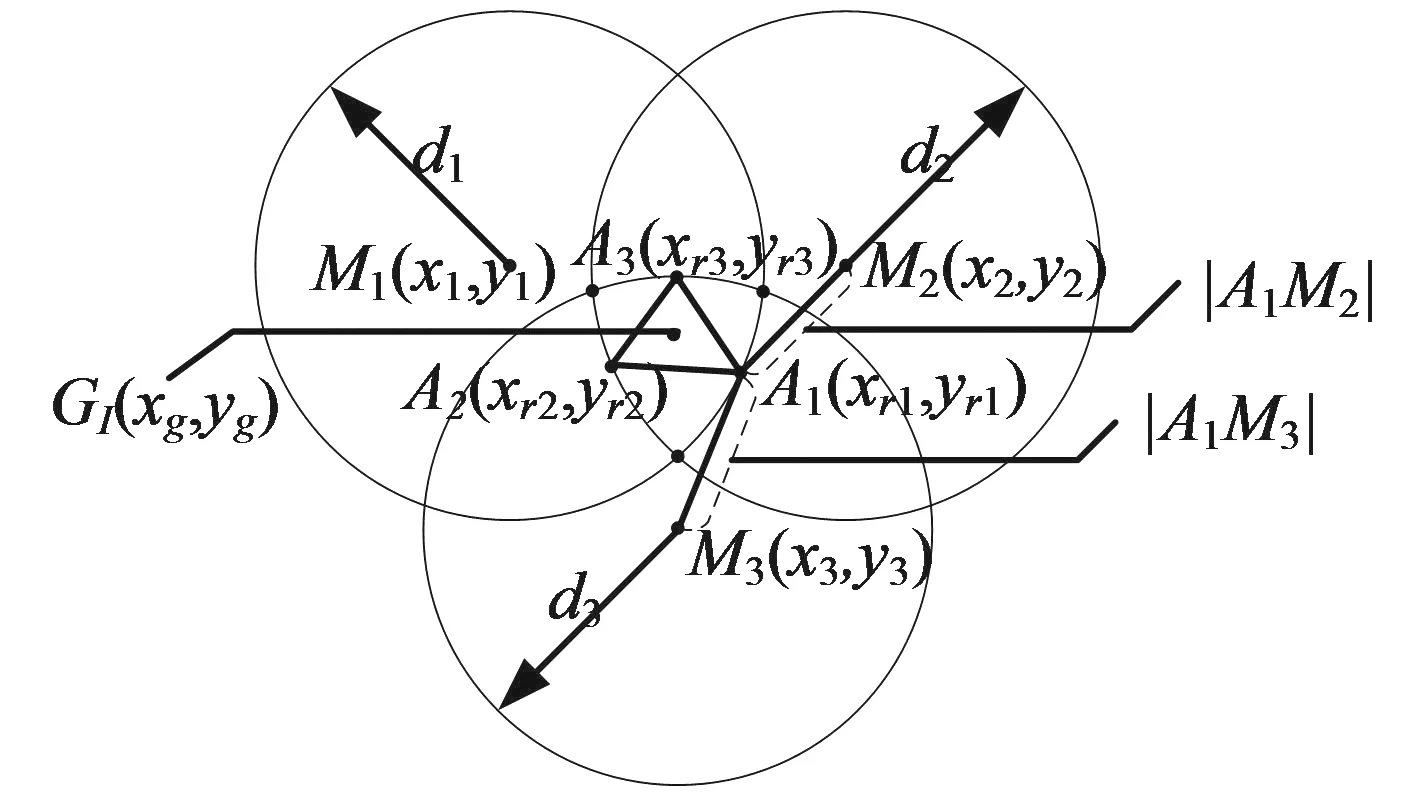
图1 参考点的计算原理图

图1中，由于A1(xr1,yr1)在以信标节点M1(x1,y1)为圆心、M1与目标节点间的距离d1为半径的圆周上，于是有：

(xr1-x1)2+(yr1-y1)2=d12.

(3)

同时，A1(xr1,yr1)需要满足的条件可由式(4)来表示：

(4)

式(4)中，d2和d3分别是圆M2和圆M3的半径，|A1M2|、|A1M3|分别是参考点A1(xr1,yr1)和信标节点M2(x2,y2)、M3(x3,y3)之间的距离，可表示为：

(5)

(6)

由式(3)-式(6)计算出的参考点A1可能会有多解，只需要保留ΔM1M2M3内部的解A1(xr1,yr1)，通过以下方法判断：①点A1和点M1位于直线M2M3同侧；②点A1和点M2位于直线M1M3同侧；③点A1和点M3位于直线M1M2同侧.如果以上3个条件同时满足，则参考点A1位于ΔM1M2M3内部，否则参考点A1位于ΔM1M2M3外部.同理，可以计算得到圆M2和圆M3上的参考点A2(xr2,yr2)和A3(xr3,yr3).

将上述所求的3个参考点作为顶点构成一个三角形，以这个三角形的质心作为目标节点的初始定位坐标GI(xg,yg)，其可由公式(7)获得.

(7)

2.2 距离偏差因子的计算

在上述参考点的基础上，引入距离偏差因子，根据距离偏差因子重新计算给定信标节点与未知目标节点之间的距离，并进一步计算新的参考点，通过不断迭代更新参考点，计算目标节点的坐标.

将上述目标节点的初始定位坐标与信标节点坐标之间的距离记为dOi，采用LDPL模型计算出目标节点和信标节点的距离，记为dIi，距离偏差因子Ci可由式(8)定义，用于表示dIi和dOi之间的偏差程度.

Ci=dIi/dOi，

(8)

式中，I为参考点的迭代次数,i= 1, 2, 3.

每次迭代可计算出3个距离偏差因子，通常采用它们的平均值和中位数作为统计总体特征的参数.由于可能会出现3个距离偏差因子的极值太大或太小的情况，其平均值用于计算会使得最终结果偏离实际值，因此通常采用它们的中位数(记为Cmid)来表达总体距离偏差特征，基于Cmid重新计算信标节点与目标节点间距离(记为d(I+1)i)，其可由式(9)表示：

d(I+1)i=dIi/Cmid.

(9)

基于新的距离d(I+1)i对参考点进行迭代，进而不断更新目标节点的定位坐标.

2.3 迭代次数的确定

迭代定位算法的关键在于终止条件的设置，如果设置正确的终止条件，可以在少量的迭代次数内获得较高的定位精度.常用的迭代准则有预设精度和预设迭代次数两种.然而通过仿真发现，如果终止条件设置成前者时，它的计算复杂度将变得很高，甚至高于算法本身.因此，选择预设迭代次数作为迭代的终止条件.

为了确定合适的迭代终止次数，在不同的节点通信半径(通信半径R=10 m和R=20 m)及不同的信标节点数量(信标节点数量J=10和J=20)条件下进行了20次迭代仿真.每次迭代对应的平均定位误差率如图2所示.

由图2可以看出，在不同的条件下，迭代次数小于6时，平均定位误差率随着迭代次数的增加而减小，迭代6次以后不再变化，即目标节点的定位精度达到收敛，因此本文将迭代终止次数设置为6次.参考点迭代定位算法的具体流程如图3所示.

图2 不同迭代次数的平均定位误差率

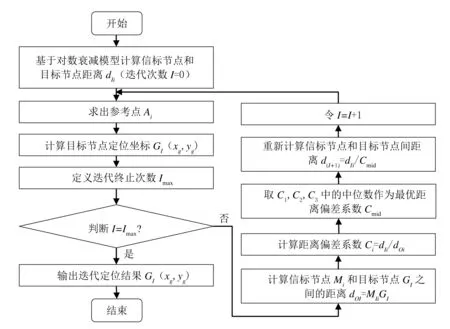
图3 参考点迭代定位算法流程图

3 仿真实验与分析

3.1 仿真环境参数设置

在MATLAB R2016b环境下进行基于DBSCAN的参考点迭代定位算法的性能仿真实验.定位区域设置为一个50 m×50 m的二维平面，区域内随机布置20个信标节点和30个目标节点.在测距模型中，节点间距为1 m时的接收信号强度A设置成-45 dBm，路径损耗因子n设置成3，添加了均值为0和标准差为2.5的高斯随机变量.

(10)

(11)

式中，r是节点的通信半径，(Xg,Yg)是目标节点的真实位置，(xg,yg)是目标节点的估计位置，N是目标节点的个数.

3.2 仿真过程及结果

为了验证本文提出的参考点迭代定位算法的可行性，构建一个边长为50 m的正方形定位区域，区域内内随机布置20个信标节点和30个目标节点，每个节点之间的通信半径设为20 m，节点分布如图4所示.采用TCP算法、WCP算法和IPAoRP对目标节点进行定位，定位结果分别如图5-图7所示.

上述3种定位算法针对目标节点的定位坐标如表1所列.

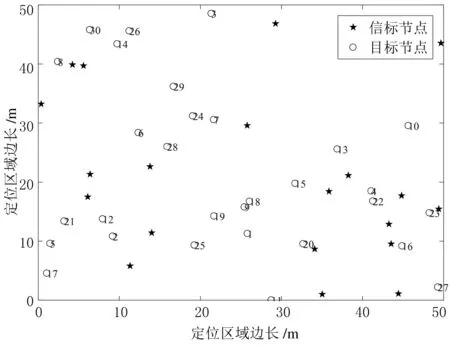
图4 信标节点和目标节点的分布图

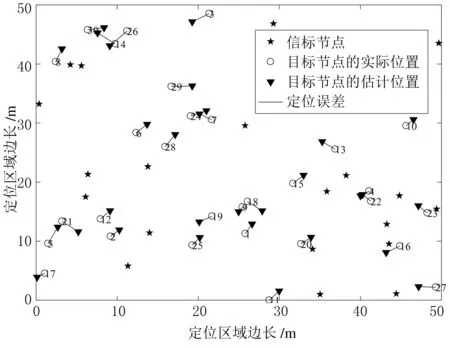
图5 TCP定位结果

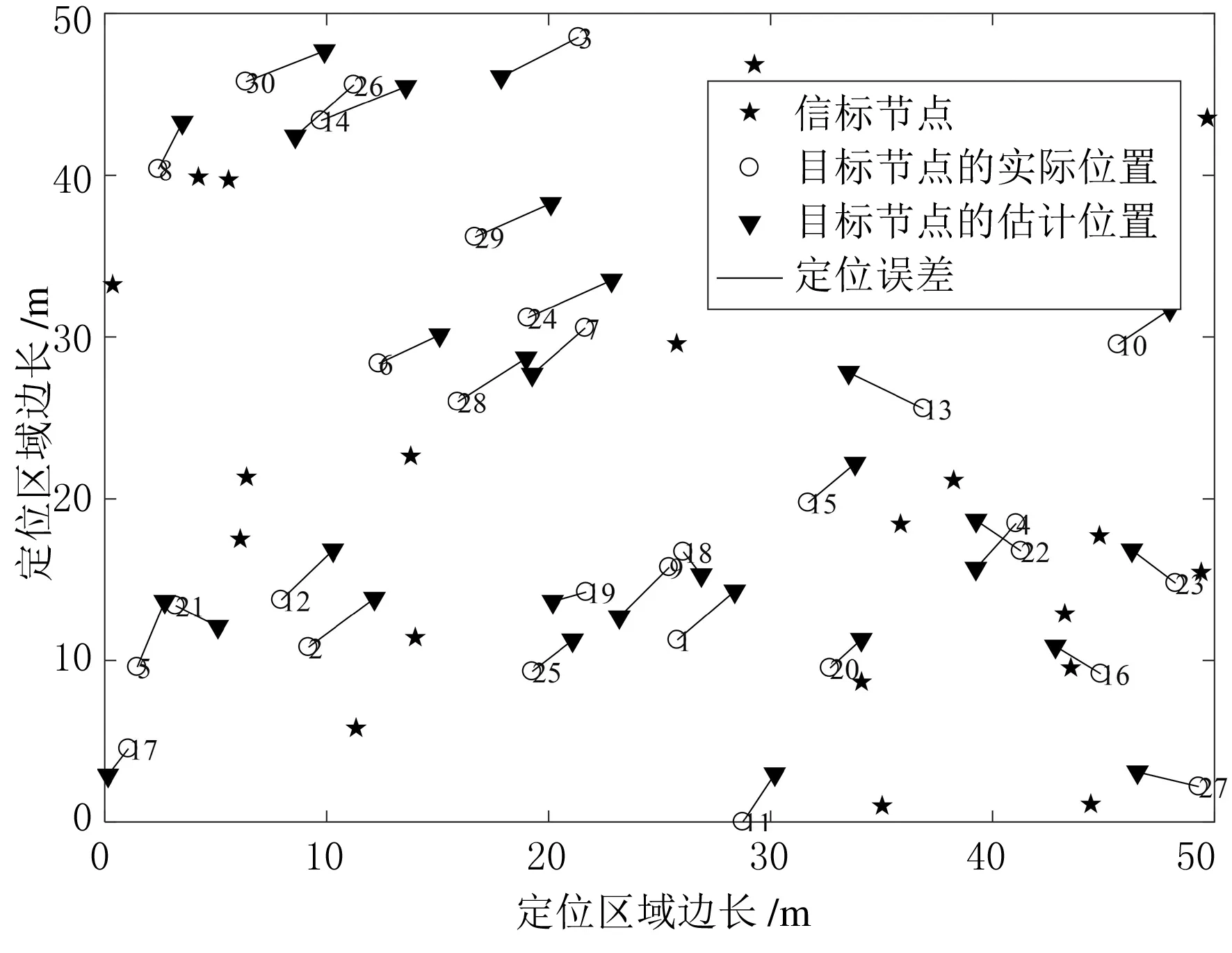
图6 WCP定位结果

图7 IPAoRP定位结果

表1 3种定位算法目标节点的定位坐标

基于式(10)计算出目标节点的定位误差率，如表2所列，误差率对比情况如图8所示.

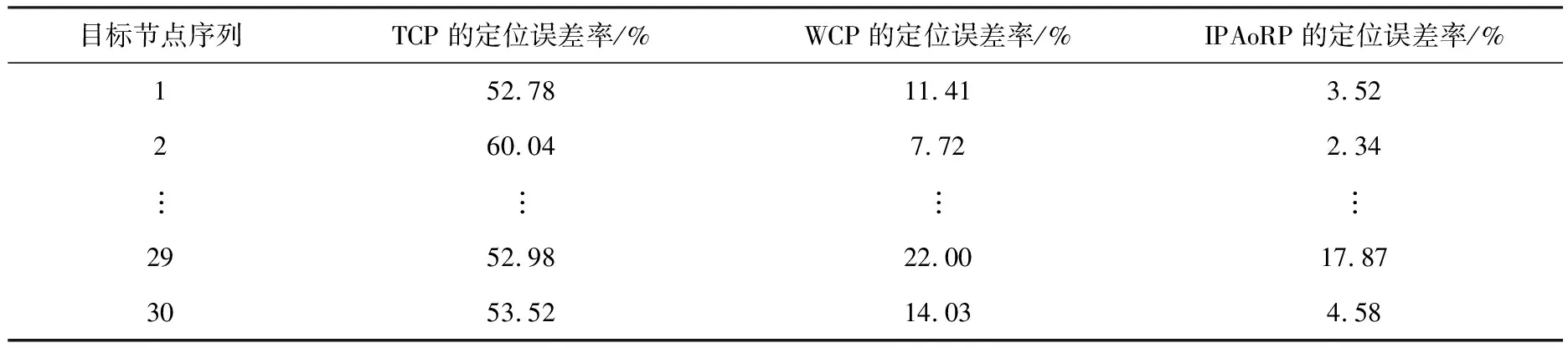
表2 3种定位算法的定位误差率

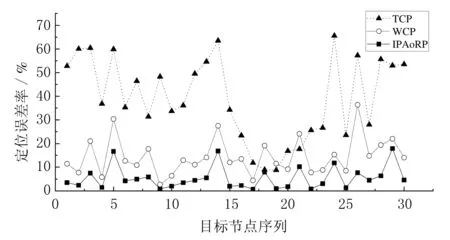
图8 3种定位算法的定位误差率对比

基于式(11)可计算出3种定位算法的平均定位误差率，如表3所列.

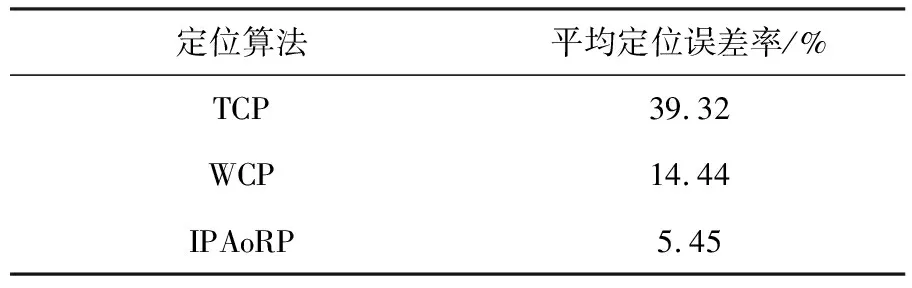
表3 3种定位算法的平均定位误差率

由表2、3和图8可知：①IPAoRP的定位误差率明显小于另外两种定位算法的定位误差率；②IPAoRP的平均定位误差率为5.45%，比TCP算法的平均定位误差率低33.87%，比WCP算法的平均定位误差率低8.99%.

4 结论

本文针对RSSI信号传输过程中噪声干扰导致定位精度降低的问题，提出了一种基于距离偏差因子的WSN参考点迭代定位算法.基于节点间的距离计算3个参考点，以其质心作为目标节点的初始坐标，引入距离偏差因子对参考点进行迭代，进而迭代目标节点的坐标.解决了传统质心定位算法定位圆不相交而无法定位的问题，提高了定位的精度.接下来将在本文提出的定位算法的基础上进一步开展无线传感器网络中移动节点的实时跟踪、路径规划等相关研究.